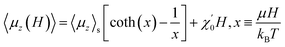Homo- and heterometallic coordination networks based on linear trinuclear Co(II) units: syntheses, structures and magnetic properties

Abstract

Two three-dimensional (3D) coordination networks, [Co₃(1,4-BDC)3(L¹)]_∞ (L¹ = N,N′-bis(3-pyridinyl)-1,4-benzenedicarboxamide; 1,4-H₂BDC = 1,4-benzenedicarboxylic acid), 1, and [K₂Co₃(L²)₄]_∞ (H₂L² = 5-acetamidoisophthalic acid), 2, have been synthesized by hydrothermal reactions and characterized by single crystal X-ray crystallography. Complex 1 consists of linear trinuclear Co(II) centers, which are linked by the 1,4-BDC⁻ and L¹ ligands to form a rare (1 + 3) self-catenated 3D net with the new (3⁶,4¹⁰,5¹¹,6) topology, and complex 2 reveals a 3p–3d heterometallic coordination network based on linear trinuclear Co(II) and dinuclear K(I) centers bridged by the μ₆-L² ligands, forming a 4,4,8-connected trinodal net with the new (4¹⁴·6¹⁰·8⁴)(4²·6⁴)(4⁴·6²) topology. The linear trinuclear Co(II) centers in 1 adopt the square pyramidal–octahedral–square pyramidal geometries, whereas those in 2 are tetrahedral–octahedral–tetrahedral. Both of the complexes exhibit paramagnetism that is consistent with the Curie–Weiss law between 60 and 300 K. The effective magnetic moments (〈μ_eff〉) of both complexes are larger than the estimated value of 6.71 μ_B/f.u., revealing the spin–orbit couplings that are invoked by the different distorted geometries of the linear trinuclear Co(II) centers. The dinuclear K(I) centers in 2 weaken the magnetic coupling, and reduce the antiferromagnetic ordering at 6 K.

---

Introduction

The synthesis and structural characterization of coordination polymers have attracted much attention not only due to their numerous potential applications in catalysis, separation, storage and magnetism, but also their intriguing structure and diverse topologies.¹ The framework topologies of these new complexes thus prepared rely on the coordination ability, geometry, and relative orientation of the donor group of the organic ligand, as well as the nature of the metal ions and counterions.² A significant number of coordination polymers containing polydentate carboxylate ligands have been prepared and well characterized,³ in which the carboxylate groups display a variety of bonding modes involving monodentate terminal, chelating, monodentate bridging and bidentate bridging. Among the polynuclear metal carboxylate complexes, those involving Co(II) ions have attracted attention due to their possible formation of a wide variety of geometries and interesting magnetic and optical properties.⁴ Moreover, the formation of the bridge by the carboxylate groups can inspire spin communication between adjacent paramagnetic metal ions. A dicarboxylate ligand with extra donor atom may lead to the formation of the heterometallic complex and it is expected that the adjacent metal units will not only affect the topology of the Co(II) coordination network but also its magnetic property.

To investigate the effect of the adjacent hetero-metal atoms on the magnetic properties of coordination networks containing the linear trinuclear Co(II) units, we have synthesized the homonuclear complex [Co₃(1,4-BDC)₃(L¹)]_∞ (L¹ = N,N′-bis(3-pyridinyl)-1,4-benzenedicarboxamide; 1,4-H₂BDC = 1,4-benzenedicarboxylic acid), 1, and the heteronuclear complex [K₂Co₃(L²)₄]_∞ (H₂L² = 5-acetamidoisophthalic acid), 2. In contrast to the extensive structural and magnetic studies on compounds with discrete trinuclear Co(II) metal centers and their extended systems,⁴ no heterometallic coordination network containing both linear trinuclear Co(II) and dinuclear K(I) units as shown in 2 has been reported. In the 3D porous metal–organic framework {[KCo₃(C₆H₄O₇)(C₆H₅O₇)(H₂O₂)₂]·8H₂O}_n that displays canted antiferromagnetic property, the tetrahedral Co(II) ions form trigonal nodes and the tetranuclear cobalt citrate clusters establish octahedral linkers with mononuclear K(I) ions locating nearby.^3b Herein, we report the synthesis, structures and magnetic properties of 1 and 2.

Experimental section

General procedures

IR spectra (KBr disk) were obtained from a JASCO FT/IR-460 plus spectrometer. Elemental analyses were performed on a PE 2400 series II CHNS/O analyzer or a HERAEUS VaruoEL analyzer. Thermogravimetric analyses (TGA) were carried on SII Nano Technology Inc. TG/DTA 6200 over the temperature range of 30 to 900 °C at a heating rate of 10 °C min⁻¹ under a nitrogen atmosphere.

Materials

The reagents Co(NO₃)₂·6H₂O, t-BuOK and 1,4-H₂BDC were obtained from Yakuri Chemicals. The ligands N,N′-bis(3-pyridinyl)-1,4-benzenedicarboxamide (L¹)^5a and 5-acetamidoisophthalic acid (H₂L²) were prepared according to published procedures.^5b

Preparations

[Co₃(1,4-BDC)₃(L¹)], 1. A mixture containing Co(NO₃)₂·6H₂O (0.087 g, 0.30 mmol), 1,4-H₂BDC (0.050 g, 0.30 mmol), L¹ (0.032 g, 0.10 mmol) and 10 mL CH₃OH/DMF (1 : 3, v/v) was placed in a 23 mL Teflon lined stainless container. The container was then sealed and heated at 140 °C for 72 h under autogeneous pressure and then cooled slowly to room temperature. Purple block crystals were collected, washed by ether and then dried under vacuum. Yield: 0.113 g (67%, based on Co). Anal calcd for 1·DMF·CH₃OH (MW = 1092.61): C, 50.57; H, 3.41; N, 6.41. Found: C, 50.21; H, 3.81; N, 6.75%. IR (cm⁻¹): 3242(w), 2361(w), 2330(m), 1662(s), 1541(s), 1385(s), 1287(m), 1105(s), 1017(w), 813(w), 746(s), 698(m), 526(m).

K₂Co₃(L²)₄, 2. A mixture containing Co(NO₃)₂·6H₂O (0.15 g, 0.5 mmol), t-BuOK (0.11 g, 1.0 mmol) and H₂L² (0.22 g, 1.0 mmol) in 10 mL THF/MeOH (1 : 1, v/v) was placed in a 23 mL Teflon lined stainless container. The container was then sealed and heated at 140 °C for 72 h under autogeneous pressure and then cooled slowly to room temperature. Purple plate crystals were collected, washed by diethyl ether and then dried under vacuum. Yield: 0.14 g (72%, based on Co). Anal. calcd for C₄₀H₂₈Co₃K₂N₄O₂₀ (MW = 1139.65) C, 42.15; H, 2.48; N, 4.92%. Found: C, 41.65; H, 2.17; N, 4.45%. IR (cm⁻¹): 3318(m), 3310(m), 1685(m), 1659(m), 1624(s), 1581(s), 1560(s), 1452(m), 1434(m), 1461(s), 1347(s), 1286(m), 1251(m), 1134(w), 1103(w),1029(w), 978(w), 934(w), 899(w), 804(w), 779(m), 722(m), 698(w), 601(w), 537(w).

X-ray crystallography

The diffraction data of complexes 1 and 2 were collected at 22 °C on a Bruker AXS SMART APEX II CCD diffractometer equipped with a graphite-monochromated MoK_α (λ_α = 0.71073 Å) radiation. Data reduction was carried out by use of well-established computational procedures. The structure factors were obtained after Lorentz and polarization correction. An empirical absorption correction based on a series of “multi-scan” was applied to the data.⁶ The positions of the heavier atoms were located by the direct method. The remaining atoms were found in a series of alternating difference Fourier maps and least-square refinements, except that the hydrogen atoms were added by using the HADD command in SHELXTL 5.10.⁷ Due to serious disorder problems of the co-crystallized solvents of 1, the SQUEEZE/PLATON technique⁸ was applied to remove the solvent contribution in the reflection data. The relevant CIF data without the solvent contribution is given as the ESI.† Basic information pertaining to crystal parameters and structure refinement are summarized in Table 1.

Table 1 Crystal data for complex 1 and 2

a R1 = ∑‖F0| − |Fc‖/∑|F0|.b wR2 = [∑w(F0^2 − Fc^2)^2/∑w(F0^2)^2]^1/2. w = 1/[σ^2(F0^2) + (ap)^2 + (bp)], p = [max(F0^2 or 0) + 2(Fc^2)]/3. a = 0.0344, b = 0, 1; a = 0.0653, b = 0, 2.c Quality-of-fit = [∑w(|F0^2| − |Fc^2|)^2/Nobserved − Nparameters]^1/2.
Compound	1	2
Formula	C42H26Co3N4O14	C40H28Co3K2N4O20
Formula weight	987.46	1139.65
Crystal system	Monoclinic	Monoclinic
Space group	C2/c	C2/c
a, Å	31.3901(7)	26.5485(4)
b, Å	10.9106(2)	9.4823(1)
c, Å	15.8458(3)	18.7577(3)
α, °	90	90
β, °	90.553(1)	101.185(1)
γ, °	90	90
V, Å^3	5426.69(19)	4632.39(11)
Z	4	4
dcalc, Mg m^−3	1.209	1.634
F(000)	1996	2300
μ(Mo Kα), mm^−1 range (2θ) for data collection, deg	0.963, 3.96 ≤ 2θ ≤ 56.72	1.324, 3.12 ≤ 2θ ≤ 56.66
Independent reflections	6739, [R(int) = 0.0634]	5748, [R(int) = 0.0547]
Data/restraints/parameters	6739/0/304	5748/0/311
Quality-of-fit indicator^c	1.010	1.010
Final R indices [I > 2σ(I)]^a^,^b	R1 = 0.0509, wR2 = 0.0944	R1 = 0.0509, wR2 = 0.1113
R indices (all data)	R1 = 0.1044, wR2 = 0.1022	R1 = 0.0984, wR2 = 0.1263

---

Magnetic susceptibility measurement

Magnetic susceptibility measurements were performed using MPMS-XL (SQUID) from Quantum Design with the standard setup. The samples were cooled to 1.8 K in the absence of an applied magnetic field at the center of signal pickup coils. χ–T experiments were carried out using both the zero field cooling (ZFC) and the field cooling (FC) methods to determine the ordering temperature of samples. Magnetic hysteresis loops were measured to study the magnetization responses to various applied magnetic fields (M–H curve), and to determine the thermal average of the z component of the saturated magnetic moment 〈μ_z〉_s per chemical formula unit.

Results and discussion

Structure of 1

Crystals of 1 conform to the space group C2/c and each asymmetric unit contains one and a half cobalt(II) cations, one and a half BDC²⁻ and a half L¹ ligands. Fig. 1(a) depict the coordination environments about the linear trinuclear Co(II) centers. The central Co(II) ion is located at an inversion center and coordinated by six oxygen atoms from two μ₂:η¹, η¹-and four μ₂:η¹,η²-BDC²⁻ ligands, resulting in a distorted octahedral geometry, whereas the adjacent Co(II) ions are coordinated by one nitrogen and four oxygen atoms, forming distorted trigonal bipyramidal geometries, with Co–N = 2.067(3) Å and Co–O = 2.181 Å in the axial positions and Co–O = 1.968(2)–2.134(2) Å in the equatorial positions. The Co⋯Co distance is 3.4193(4) Å. The adjacent linear trinuclear Co(II) units are linked by the BDC²⁻ and L¹ ligands to form a 3D coordination network. Considering the centers of the linear trinuclear Co(II) as the 8-connected nodes and the BDC²⁻ and L¹ ligands are transformed as links, topological analysis using TOPOS⁹ reveals that complex 1 forms a uninodal 8-connected coordination network with the new (3⁶,4¹⁰,5¹¹,6) topology, Fig. 1(b).

Fig. 1 (a) Coordination environment about the Co(II) centers of 1. (b) A schematic drawing of the 8-connected uninodal net, highlighting the (1 + 3) catenation mode.

The striking feature of this topology is the cross-linking of the 2D 3⁶ nets pillared by the rods formed by the L¹ ligands, resulting in the self-catenation. As highlighted in Fig. 1(b), each shortest six-membered ring is catenated by three rods of the same network, i.e., (1 + 3) catenation, which is in marked contrast to the (1 + 1) and (1 + 2) catenations found for rob and mab topologies, respectively. The (1 + 3) mode of the roa topology can be found for the compounds {[Zn₂(4-Br-ip)₂(bpy)]·3H₂O}_n (4-Br-H₂ip = 4-bromo- or 5-bromoisophthalic acid; bpy = 4,4′-bipyridine) and Cd(CN)·bpb [bpb = 1,4-bis(4-pyridyl)butadiyne] that are listed in the TTO database of TOPOS,⁹ where the 2D layers that pillared by the rods adopt the 4⁴ topology.

Structure of 2

Crystals of 2 conform to the space group C2/c and each asymmetric unit contains two Co(II) cations, one K(I) cation and two L² ligands. Fig. 2(a) displays the 3D structure of 2 and Fig. 2(b) and (c) depict the coordination environments about the linear trinuclear Co(II) and dinuclear K(I) centers, respectively. Each of the bilateral Co(1) centers is coordinated by four carboxylate oxygen atoms [Co–O = 1.940(2)–2.006(2) Å] to form a distorted tetrahedral geometry, whereas the central Co(2) center, which is located at the crystallographic inversion center, shows a distorted octahedral geometry with the metal atom coordinated by six carboxylate oxygen atoms [Co–O = 1.989(2)–2.271(2) Å]. The adjacent Co(II) ions are separated by a distance of 3.2277(4) Å. The K(I) centers adopt the distorted square pyramidal geometries, which are coordinated by three carboxylate oxygen atoms [K–O = 2.584(3)–2.791(2) Å] and one amide oxygen atoms [K–O = 2.859(3) and 2.754(4) Å] at the square base and one amide oxygen atom at the apical position. The adjacent trinuclear Co(II) and dinuclear K(I) units are linked by the L² ligands with the shortest Co⋯K distance of 3.7543(10) Å, whereas the K⋯K distance of 3.735 (2) Å is shorter than that of the van der Waals contact of K atoms which is 5.50 Å.

Fig. 2 (a) A drawing showing the 3D structure of 2. (b) Coordination environments about the Co(II) ions. (c) Coordination environments about the K(I) ions.

The μ₆-L² ligands adopt two types of bonding modes, Fig. 3(a). While one of the μ₆-L² ligands bridges four Co(II) and two K(I) cations, the other bridges three Co(II) and three K(I) cations. It is noted that while the carboxylate oxygen atoms coordinate to both of the Co(II) and K(I) cations, the amide oxygen atoms coordinate only to the K(I) cations. Considering both of the linear trinuclear Co(II) and the dinuclear K(I) units as the 8-connected nodes, Fig. 3(b), and the μ⁶-L² ligands as the 4-connected nodes, Fig. 3(a), topological analysis using TOPOS⁹ reveals that complex 2 forms a trinodal 4,4,8-connected coordination network with the new (4¹⁴·6¹⁰·8⁴)(4²·6⁴)(4⁴·6²) topology, Fig. 3(c).

Fig. 3 (a) Bonding modes and the 4-connected nodes for the L² ligand. (b) The 8-connected nodes for the trinuclear Co(II) and dinuclear K(I) units. (c) A drawing showing the 4,4,8-connected trinodal net.

Thermal properties

The TGA curve of complex 1, Fig. S1,† shows the gradual weight loss of 10.72% in 50–190 °C, which is due to the removal of CH₃OH and DMF molecules (calcd 9.64%). This weight loss indicates that each formula of 1 is supposed to contain one CH₃OH and one DMF molecules, which have been squeezed out during structural determination. This suggestion is consistent with the elemental analysis as shown in the Experimental section. The second weight loss of 65.62% in 410–900 °C can be ascribed to the decomposition of L¹ and 1,4-BDC²⁻ ligands (calcd 67.61%). For complex 2, Fig. S2,† the weight loss of 72.0% occurs between 320 and 900 °C, corresponding to the decomposition of the L² ligands (calcd 72.7%).

Magnetic properties

The test samples were obtained by thoroughly grounding the single crystals of 1 and 2. Attempts were then made to ensure the consistency of the crystal structures after grinding by using powder X-ray diffraction and Rietveld refinement. Fig. S3 and S4† show that the calculated and observed spectra match quite well, indicating no structural change or decomposition for 1 and 2 during grinding. The ordering temperatures of the samples were then determined by conducting χ–T experiments. Table 2 lists all of the fitting parameters.

Table 2 Fitted magnetic parameters of 1 and 2

M–H	Complex 1	Complex 2
Ms (emu g^−1)	25(1)	34.89(2)
〈μz〉s (μB/f. u. at 2 K)	5.30(3)	4.28(6)
χ^′0 (10^−5 μB/f. u. Oe at 2 K)	7(2)	4.69(9)

---

χ–T	FC 50 Oe	ZFC 50 Oe	FC 50 Oe	ZFC 50 Oe	ZFC 1T
χ0 (10^−6 emu g^−1 Oe)	2.3(5)	3.1(1)	8(2)	5(4)	−10(4)
C (10^−3 emu K g^−1 Oe)	6.85(12)	6.65(3)	6.35(11)	6.56(6)	8.23(2)
μeff (μB/f.u.)	7.36(6)	7.25(2)	7.61(3)	7.74(6)	8.66(9)
Tθ (K)	7.43(93)	6.04(25)	0.95(3)	1.10(6)	3.64(14)
A (10^−3 emu K g^−1 Oe)	1.96(1)	1.87(7)	1.22(3)	1.19(3)	0.62(6)
B (10^−3 emu K g^−1 Oe)	6.25(12)	6.37(9)	6.41(3)	6.47(3)	6.95(4)
E1 (meV) (in unit of K)	13.5(9)	14.8(9)	3.96(30)	4.52(37)	7.89(82)
	157(10)	172(10)	46(4)	53(4)	92(10)
E2 (10^−2 meV) (in unit of K)	11.1(7)	18.95(61)	7.24(22)	7.64(23)	15.34(35)
	1.28(8)	2.20(7)	0.84(3)	0.89(3)	1.78(4)

---

Fig. 4(a) presents the collected temperature profiles for 1. A magnetic susceptibility peak started at about 60 K and reached its maximum value at 6 K (as zero field cooling, ZFC), which is associated with an antiferromagnetic ordering (AFM) of Co ions. The modified Curie–Weiss law

was employed to fit the ZFC curves. Here, C is the Curie constant; T is the measured temperature, and T_θ is the Weiss temperature. Positive and negative signs of T_θ represent antiferromagnetic and ferromagnetic (FM) interaction of magnetic ions, respectively. If the measured χ belongs to the unit of “emu/g-Oe”, that is χ_mass, the effective magnetic moment, μ_eff, can be simply extracted from Curie constant C by the relation of μ_eff = 2.828(MC)^1/2, here M is per formula weight. Linear part of the 1/χ–T curve is utilized to determine the proper temperature range of Curie–Weiss fitting. The inset in Fig. 4(a) reveals linear 1/χ–T curve between 60 and 300 K. The Weiss temperature T_θ obtained from the curve of ZFC 50 Oe is 6.04(25) K, implying a AFM interactions between Co(II) ions. Notably, the fitted effective moment (μ_eff) is 7.25(2) μ_B/f. u., which exceeds the calculated value of 6.71 μ_B/f. u. (S = 3/2, g = 2, μ_eff = g[Σμ_eff²(Co(II))]^1/2 = 2·[3·(3/2·5/2)]^1/2 ≅ 6.71 μ_B/f. u.). The is known to satisfy,
where J is total angular moment; L is the total orbital angular moment, and S is the total spin angular moment. For general 3d transition metals, the total orbital angular moment is quenched owing to the symmetry of the crystal field of surrounding ions, reducing L to zero and yielding g = 2. When structural distortion breaks the symmetry of the crystal field, L becomes finite and g deviates from two. A simple calculation (2 × 7.25/6.71) demonstrates that the g value of 1 is 2.16, which implies the existence of spin–orbit coupling of Co(II) ions.

Fig. 4 (a) χ–T and (b) χT–T curves for 1 with their fitting curves (inset) of varies cooling process. (c) M–H curves for 1 with Langevin fitting curves at 2 K.

To determine whether spin–orbit coupling exists, Rueff's equation,¹⁰

is utilized. Here, the sum of A and B equals the Curie constant C, and E₁ and E₂ denote the “activation energies” of spin–orbit coupling and the antiferromagnetic exchange interaction, respectively. This equation describes well the χT curve of 1 between the temperatures of 60 K and 300 K. As shown in Fig. 4(b) and Table 2, the sums of A and B are close to the Curie constant C, as obtained from the Curie–Weiss law. Activation energy of antiferromagnetic exchange interaction, E₂, also approaches the fitted value of T_θ. The activation energy, E₁, indicates the existence of spin–orbit coupling. The order of magnitude of E₁ is a factor of 2 larger than E₂, which shows the deviation from Curie–Weiss law at the low temperatures. A small E₂ value describes the paramagnetism behavior. A relatively strong E₁ value implies that a larger μ_eff is associated with non-negligible spin–orbit coupling, possibly increasing the Landé g-factor (from 2 to a larger value) or reducing the quench of orbit angular moment J (becomes nonzero) in the equation μ_eff = g[J(J + 1)]^1/2. The distorted square pyramidal and octahedral geometries of the linear trinuclear Co(II) ions result in the asymmetric crystal field for the Co(II) ions. This environmental factor may explain the reduced quenching effect of the orbital angular momentum and further explain the existence of E₁.

Fig. 4(c) shows the hysteresis of 1 at 1.8 K and 300 K. The magnetizations increase linearly with the applied magnetic field below 1 T at both 1.8 K and 300 K and gradually approach saturation at 1.8 K in a field of 7 T. The Langevin function

was applied to the curve to yield 〈μ_z〉_s (saturation 〈μ_z〉). The obtained 〈μ_z〉_s of the sample at 2 K is 5.30(3) μ_B/f. u., which is smaller than 9 μ_B f. u. (spin 3/2, g = 2, n = 3/f. u., 〈μ_z〉_s = ngJμ_B = 9 μ_B/f. u.) of the [Ar]3d⁷ electronic configuration. The declined magnetic moments may originate from the canted spin arrangement. Therefore the spins of nearest-neighbor Co(II) ions tend to exhibit an anti-parallel manner and leads to a reduction of the net magnetic moment. Otherwise, a coercivity of 604(2) G was observed in the inset of Fig. 4(b), which implied the existence of small ferromagnetic-like (FM-like) magnetic domains at 2 K. The AFM feature from χ–T curve and lack of magnetic moments from the Langevin function of M–H curve refer that these FM-like domains at 2 K come from the residue magnetic moment of canted AFM ordering. The non-canceled component of magnetic moment at AFM domain exhibits FM-like behavior and results the observation of coercivity.

Fig. 5(a) shows the magnetic susceptibility (χ–T) curve for 2, in which FC in 50 Oe, 10⁴ Oe and ZFC processes were evaluated. The linear part of the 1/χ–T curve shown as inset reveals the proper temperature range that follows Curie–Weiss law. Obviously, complex 2 exhibits paramagnetism in the temperature range 60–300 K. It is shown that the fitting parameters of χ₀, C, μ_eff, and T_θ remain unaffected by the applied magnetic fields below 10⁴ Oe. The estimated μ_eff is associated with spin state, which can be acquired from structural parameters analysis, subsequently yielding the ionic radius and their valences.^11,12 According to the bond valence method, the valence of Co(1), Co(2), and their average are 1.93(4), 2.06(5), and 1.97(9) v.u., respectively, which match the estimated value of 2.00 v.u. for Co(II).¹¹ Moreover, the average bond length of Co(2) is 2.101(5) Å, which clearly deviates from the value of low spin (LS) state of 2.003 Å and close to the high spin (HS) one of 2.098 Å.¹² Notably, no LS state is available for the Co(II) ion in the coordination number of 4 as shown for Co(1) site.¹² According to the structural parameters analysis, the Co(II) ions in 2 are all in high spin state. The estimated μ_eff should be 6.71 μ_B, which is smaller than the fitted ones.

Fig. 5 (a) χ–T and (b) χT–T curves for 2 with their fitting curves (inset) of varies cooling process. (c) M–H curves for 2 with Langevin fitting curves at 2 K.

Rueff's equation is also used to analyze the magnetic susceptibility curves. This equation well describes the χT curve of 2 over the entire temperature range. Table 2 and Fig. 5(b) present final results. The magnetic behaviors and fitting values of ZFC 50 Oe experiment above 60 K of 2 are similar to those of 1. The disappearance of the AFM susceptibility peak at 6 K reveals the relatively weak magnetic interaction of Co(II) ions. The smaller E₁ value of 2 also indicates that it exhibits a weaker spin–orbit interaction than 1. Structural analysis shows that the Co⋯Co distance in 1 is 3.4193(4) Å, and the Co(1)⋯Co(2) distance in 2 is 3.2277(4) Å. Stronger magnetic coupling and higher ordering temperature in 2 than in 1 are inferred, but the observations are to the contrary, revealing that the dinuclear K(I) center in 2 may play some important role in reducing the magnetic interaction.

The saturation magnetization, remanence, and coercivity of 2 are identified using the magnetic hysteresis loop (M–H curve). Fig. 5(c) shows the results of M–H curves. No hysteresis loop is found, implying the non-existence of a magnetic domain. The saturation magnetization is obtained by applying the following Langevin function, i.e.,

to the curve in order to yield 〈μ_z〉_s (where 〈μ_z〉 is the thermal average of the z component of the magnetic moment, and 〈μ_z〉_s represents the saturated 〈μ_z〉). The estimated 〈μ_z〉_s = g 〈J_z〉μ_B is 9 μ_B/f. u. (three Co(II) ion with [Ar]3d⁷ electron configuration in a chemical formula unit is 3 × 3 μ_B), owing to the effect of spin–orbit effect on g-factor and J_z. The obtained 〈μ_z〉_s of 2 is only 4.28(6) μ_B/f. u., which is less than half the value of the estimated one. This value is also associated with the distorted bonding environments of liner trinuclear Co(II). The Pauli exclusion principle tends to arrange the spins of the bonding valence electron when the nearest-neighbor Co ions becomes anti-parallel. The distorted bonding environments cause an incomplete cancelation of 〈J_z〉 under the applied magnetic field. The final outcome is reduced for the 〈J_z〉 and 〈μ_z〉_s in a chemical formula.

The magnetic properties of homotrinuclear complexes and their extended systems involving Co(II) ions have been reported, which frequently exhibit ferromagnetic^4a,h or antiferromagnetic^4c spin interactions. Noticeably, the 2D coordination polymer [Co₃(CTC)₆(py)₂(OH)₂] (CTC = cis,cis-cyclohexane-1,3,5-tricarboxylate) shows spin-canting ferromagnetic behavior at low temperature.^4g In this study, the magnetic susceptibility and hysteresis loop of 2 exhibit AFM behavior but is much weaker than that of 1. This behavior may be associated with the adjacent dinuclear K(I) units. The shortest Co⋯K distance in 2 is only 3.7543(10) Å, implying that the electric field from the dinuclear K(I) units may destroy the quenching of orbital angular momentum. It is seen in Fig. 2(a) that the electron exchange path along K–O–C–O–Co exhibits different electronegativity toward either side of the carbon. This geometric configuration allows the K(I) ions to influence the bonding environment, create distortions, and induce the spin–orbit interaction of Co(II) ions, which may explain why the Co(II) ions in 2 interacts antiferromagnetically but behaves paramagnetically, and differs critically from the homometallic systems. A comparison of the magnetic properties of 1 and 2 with those reported^4a–h indicates that the coordination environments about the linear trinuclear Co(II) units play an important role in determining the magnetism.

Conclusions

We have successfully synthesized and characterized a homometallic and a heterometallic coordination networks based on linear trinuclear Co(II) units. While the former exhibits a rare (1 + 3) self-catenation with the (3⁶,4¹⁰,5¹¹,6) topology, the latter adopts the (4¹⁴·6¹⁰·8⁴)(4²·6⁴)(4⁴·6²) topology. Two types of bonding modes were observed for the μ₆-L² ligands of 2, in which the carboxylate oxygen atoms coordinate to both of the Co(II) and K(I) cations, and the amide oxygen atoms coordinate only to the K(I) cations, resulting in a heterometallic coordination network. The Curie–Weiss law accurately describes the χ–T curves of both complexes in 60–300 K, revealing paramagnetism in this temperature range. The different distorted geometries of the Co(II) ions lead to spin–orbit couplings and govern the magnetic behaviors below 60 K, whereas the dinuclear K(I) units weaken the magnetic properties of 2 by changing the coordination environments of the Co(II) ions.

Acknowledgements

We thank the Ministry of Science and Technology of the Republic of China for financial support, under Grants MOST 102-2113-M-033-005-MY3 and MOST 103-2112-M-033-003.

References

1. (a) N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keefe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176; (b) S. R. Batten, S. M. Neville and D. R. Turner, Coordination Polymers: Design, Analysis and Application, Royal Society of Chemistry, Cambridge, 2009; (c) S. Kitagawa and R. Matsuda, Coord. Chem. Rev., 2007, 251, 2490; (d) J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869.
2. (a) H.-H. Li, Z.-R. Chen, J.-Q. Li, C.-C. Huang, Y.-F. Zhang and G.-X. Jia, Cryst. Growth Des., 2006, 6, 1813; (b) Y.-H. Wang, K.-L. Chu, H.-C. Chen, C.-W. Yeh, Z.-K. Chan, M.-C. Suen, J.-D. Chen and J.-C. Wang, CrystEngComm, 2006, 8, 84; (c) X.-H. Bu, W. Chen, W.-F. Hou, M. Du, R.-H. Zhang and F. Brisse, Inorg. Chem., 2002, 41, 3477; (d) A. J. Blake, N. R. Champness, P. A. Cooke, J. E. B. Nicolson and C. Wilson, J. Chem. Soc., Dalton Trans., 2000, 3811.
3. (a) H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444; (b) S. Xiang, X. Wu, J. Zhang, R. Fu, S. Hu and X. Zhang, J. Am. Chem. Soc., 2005, 127, 16352.
4. (a) Y.-T. Yang, F.-H. Zhao, Y.-X. Che and J.-M. Zheng, Inorg. Chem. Commun., 2011, 14, 1802; (b) W. Zhuang, H. Sun, H. Xu, Z. Wang, S. Gao and L. Jin, Chem. Commun., 2010, 46, 4339; (c) F. Hu, H. Zou, X. Zhao, Y. Mi, C. Luo and Y. Wang, CrystEngComm, 2013, 15, 1068; (d) M.-X. Yao, M.-H. Zeng, H.-H. Zou, Y.-L. Zhou and H. Liang, Dalton Trans., 2008, 2428; (e) P. Kapoor, A. P. S. Pannu, G. Hundal, R. Kapoor, M. Corbella, N. Aliaga-Alcalde and M. S. Hundal, Dalton Trans., 2010, 39, 7951; (f) S. Sha, H. Yang, J. Li, C. Zhuang, S. Fao and S. Liu, Catal. Commun., 2014, 43, 146; (g) S. Khatua, S. Goswami, S. Parshamoni, H. S. Jena and S. Konar, RSC Adv., 2013, 3, 25237; (h) Y.-Q. Wang, A.-L. Cheng, X. Wang and E.-Q. Gao, RSC Adv., 2012, 2, 10352; (i) J. H. Yoon, D. Kim, X. Song, S. Han, J. Shin, S. B. Hong and M. S. Lah, RSC Adv., 2012, 2, 11566; (j) D. Kim, X. Song, J. H. Yoon and M. S. Lah, Cryst. Growth Des., 2012, 12, 4186.
5. (a) L. Rajput, S. Singha and K. Biradha, Cryst. Growth Des., 2007, 7, 2788; (b) J. M. Kelleher, S. E. Lawrence, M. T. McAuliffe and H. A. Moynihan, CrystEngComm, 2007, 9, 72.
6. Bruker AXS, APEX2, V2008.6; SADABS V2008/1; SAINT V7.60A; SHELXTL V6.14, Bruker AXS Inc., Madison, Wisconsin, USA, 2008.
7. G. M. Sheldrick, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 2008, 64, 112.
8. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7.
9. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576.
10. J.-M. Rueff, N. Masciocchi, P. Rabu, A. Sironi and A. Skoulios, Eur. J. Inorg. Chem., 2001, 2001, 2843.
11. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1991, 47, 192.
12. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.

---

Footnote

† Electronic supplementary information (ESI) available: Selected bond distances and angles (Tables S1 and S2). TGA curves (Fig. S1 and S2). Powder XRD patterns (Fig. S3 and S4). CCDC 1043101 and 1043102. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ra00728c

---