Tetrathiafulvalene derivatives as cation sensor: density functional theory investigation of the hyper-Rayleigh scattering first hyperpolarizability†
Chun-Guang Liu*ab,
Ming-Li Gaoa,
Shuang Liua and
Ding-Fan Zhanga
aCollege of Chemical Engineering, Northeast Dianli University, Jilin 132012, P. R. China. E-mail: liucg407@163.com; liucg407@mail.nedu.edu.cn; Fax: +86 0432 64806919; Tel: +86 0432 64806919
bInstitute of Functional Material Chemistry, Faculty of Chemistry, Northeast Normal University, Changchun 130024, P. R. China
First published on 29th April 2015
Abstract
The hyper-Rayleigh scattering (HRS) first hyperpolarizability of a series of extended (ex) tetrathiafulvalene (TTF) and TTF derivatives have been theoretically investigated using density functional theory (DFT) with the CAM-B3LYP functional to explore their use as potential cation sensor. Among these exTTF and TTF derivatives, a compound containing the redox-active TTF unit and chelating functional group pyridine is a an effective sensor for all five kinds of metal cation (Ni2+, Cu2+, Mg2+, Zn2+, and Cd2+) studied here according to our DFT calculations. Compared with the traditional linear optical detection technology, the nonlinear optical property (HRS first hyperpolarizability) has rarely been considered to detect metal cation. Towards such goals, this compound would be useful to guide the search for potential cation sensor in new directions.
1. Introduction
The techniques of detecting metal ions have attracted considerable attention because of their potential application in chemistry, clinical biochemistry, toxicology, and environmental science, etc.1–6 In general, the detection of metal ions is mainly based on the linear optical response. By contrast, the nonlinear optical (NLO) response has rarely been considered for detecting metal ions, especially second-order NLO property.7 The advantages of second-order NLO response relevant to the linear optical response for detecting metal ions mainly come from the rich tensor component of the first hyperpolarizability.8The interaction between a light wave and matter is frequently described through the induced electrical polarization P. When a molecule is subjected to an external electric field F with high electric field strength, the molecular polarization (pi) can be written as
 | (1) |
The molecular polarization pi and the components of those tensors are functions of the frequency ω1 induced by applied wave fields of frequency ω2, ω3, …, ωs in the NLO processes. The frequency dependence of the polarization can be expressed as
 | (2) |
For the second-order NLO effect, four different kinds of phenomenon can be observed experimentally. They are second-harmonic generation [SHG; β(−2ω; ω, ω)], the linear electro-optic effect [LEOE; β(−ω; ω, 0)], sum-frequency generation [SFG; β(−ω1, −ω2; ω1, ω2)], and optical rectification [OREC; β(0; ω, −ω)]. Among them, SHG has been used in chemical monitoring, biological and chemical sensing aspects.11–13
Hyper-Rayleigh scattering (HRS) is a widely-applied technology to measure SHG responses experimentally. Kim et al. demonstrated14 that an appropriately functionalized gold nanoparticles was capable of sensing of ion contaminants in water via an ion-chelation-induced aggregation process based on their HRS studies. Their results clearly indicated that the HRS detection limit is much higher than that of linear optical spectroscopy. An enhancement of HRS responses was readily obtained with addition of as little as 25 μM Pb2+, this concentration too low to generate a visible color change. Darbha et al. reported15 that the gold nanoparticles modified by mercaptopropionic acid and pyridinedicarboxylic acid can be used for screening of Hg(II) in aqueous solution with high detection limit (5 ppb) and selectivity over competing analyses. Their experimental results indicated that the HRS intensity is highly sensitive to the concentration of Hg(II) ions, the linear correlation was shown between the HRS intensity and the concentration of Hg(II) ions over the range of 5–100 ppb, which is the same order of magnitude as the environmental protection agency standard for the maximum allowable level of Hg(II) in drinking water.
The redox-active tetrathiafulvalene (TTF) unit16 is able to exist in three different stable redox states (TTF, the radical cation TTF˙+, and dication TTF2+),17 and the oxidation to the radical cation and dication occurs sequentially and reversibly at low potentials (see Chart 1). Due to the 14π-electron structure, the TTF unit is lack of a π-electrons cyclic conjugation, and thus is nonaromatic according to Hückel rule. But the radical cation and dication with one and two 6 π-electron units are aromatic in the Hückel sense, and thus both oxidized species are thermodynamically stable. Our previous studies found that the one-electron-oxidized process made the non-planar TTF units change to a planar structure, which improved its conjugation. And thus the oxidation leads to a significant enhancement of the second-order NLO response.18–25
Recently, an extended (ex) TTF derivative, containing a furanoquinonoid spacer and pyridine functional groups, has been prepared by Sallé group26 (see Chart 2). Because of the presence of pyridine with chelating functional groups, such exTTF derivatives can coordinate with various metal ions. According to the literature, introduction of metal ions into the organic molecules would generally increase the second-order NLO response.27–47 This indicates that this kind of exTTF derivative may have a potential capability to detect metal ions.48–51
 | ||
| Chart 2 The structural formula of an exTTF derivative containing chelating pyridine functional groups. | ||
In the present paper, second-order NLO responses of a series of TTF derivatives containing the chelating pyridine functional group have been studied (see Fig. 1). The aim of this work is (i) exploration of the potential function for detecting metal ions on the basis of their HRS response; (ii) analysis of the relationship between their redox properties and second-order NLO responses.
2. Computational details
All molecular geometries were optimized and characterized as energy minima at B3LYP52–54/6-31G(d) levels (LANL2DZ basis set for metal atom). In order to obtain a more intuitive description of origin of the second-order NLO responses, time-dependent density functional theory (TDDFT) methods were used to describe the nature of excited state at CAM-B3LYP/6-31G(d) level (LANL2DZ basis set for metal atom).The dynamic and static first hyperpolarizabilities have been calculated by using TDDFT method55,56 with the long-range correction (LC) exchange-correlation functional in this work. HRS technology works equally well for neutral and charged species. In general, the dynamic first hyperpolarizability βHRS (−2ω; ω, ω) is analyzed in terms of its two contributions, originating from perpendicular light polarizations. Theoretically, Champagne et al.57,58 have developed an effective method to estimate the molecular HRS response based on quantum chemical calculations, the molecular NLO response βHRS (−2ω; ω, ω) can be expressed as Bersohn theory:
 | (3) |
For the DFT-derived hyperpolarizability, the conventional generalized gradient approximation (GGA) and the localized density approximation always tend to overestimate hyperpolarizability of donor-π-conjugated bridge-acceptor (D–π–A) system,59,60 even though the hybrid method such as B3LYP was used, the situation is not improved for large D–π–A system. The deficiency of conventional exchange functional arises from the incorrect asymptotic exchange potential behavior, which results in an underestimation of charge-transfer excitation energies, and thus a large overestimation of hyperpolarizabilities. To overcome this problem, the LC exchange-correlation functional was developed. In the LC scheme, the DFT exchange and Hatree–Fock (HF) exchange contributions are partitioned at the operator level, and the proportion of nonlocal HF contribution varies in terms of the range of the interaction. The ratio of the nonlocal HF part to the local DFT part becomes larger for greater distances. And the interelectronic Coulomb operator is separated into a short-range component and its long-range complement. These improvement approaches offer a possibility to restore the correct asymptotic exchange potential behavior for the LC functionals. The literature reported that LC-DFT methods provide better estimates for hyperpolarizabilities in charge-transfer compound when compared with hybrid and GGA functionals.61–65 Such as, the range-separated CAM-B3LYP functional with the proper consideration of the charge transfer between donor and acceptor well estimated molecular hyperpolarizability of D–π–A structure.
It is well known that the hyperpolarizability is sensitive to the electronic distribution in the fringe regions. Therefore, the basis set for calculating hyperpolarizability should involve both diffuse and polarized functions and be substantially larger than those required for calculating ground-state properties. For the metal atom, the SDD66 basis set is more flexible because of its triplet-ζ quality when compared with the double-ζ quality LANL2DZ basis set. For the main group elements, we explored basis set effects on the dynamic HRS first hyperpolarizability (βHRS) using a variety of basis sets, including 6-31G(d), 6-31+G(d), 6-31++G(d), 6-311++G(d,p), and aug-cc-pVDZ for main groups. Due to the high computational cost, only the ligand 5 has been chosen as an example to consider the basis set effects in this work. The calculated βHRS values of the ligand 5 with various basis sets have been listed in Table S1 (see ESI†). It can be found that the basis set effects on the βHRS values are rather modest, introduction of diffuse function (6-31G(d) → 6-31+G(d)) only decreases the βHRS value by 0.01 × 10−30 esu (−0.5%). Further augmentation of the basis sets (6-31+G(d) → 6-31++G(d) and 6-31++G(d) → 6-311++G(d,p)) still produces the effects on the margins, increasing the βHRS value by 0.16 × 10−30 esu (8%) and decreasing the βHRS values by 0.1 × 10−30 esu (−5%), respectively. We compare the 6-311++G(d,p) and aug-cc-pVDZ data. The results indicate that the basis set effects remain marginal, the aug-cc-pVDZ βHRS data is only 4% greater than the corresponding 6-311++G(d,p) value. Considering a balance between computational cost and accuracy, the 6-31+G(d) basis set may be an appropriate choice for our studied systems, and thus has been employed to calculate the dynamic HRS first hyperpolarizability of all compounds studied here. In the present paper, the dynamic first hyperpolarizability has been calculated at CAM-B3LYP67/6-31+G(d) levels (metal atoms using the SDD basis set). All calculations were performed using the Gaussian 09 program package.68
3. Results and discussion
3.1 Geometrical structure and second-order NLO properties
It has been reported that the ligand 1 can coordinate with various metal ions experimentally (see Chart 2). Moreover, the X-ray single crystal structure of an Ni(II) complex of the ligand 1 has been reported.26 Since the ligand 1 is a quadridentate ligand, the octahedral coordination sphere of metal center need to be completed by two additional chloride ligands. In the present paper, the geometry of this Ni(II) complex has been optimized at B3LYP level using 6-31G(d) basis sets (LANL2DZ basis sets on metal atom). The key geometrical parameters of experimental and theoretical results have been compared in Table S2.† It can be found that our DFT calculations well reproduce its geometrical structure. There is only a slight difference between calculated and experimental values, as comparison of the six bond lengths around the metal center. The calculated average bond length is 2.373 Å, which is only 0.085 Å longer than the experimental value (2.288 Å). A comparison of the key bond and dihedral angles also shows good agreement between experimental and calculated parameters (see Table S2†).As an example, the molecular geometries of the ligand 5 and a metal complex optimized by our DFT calculations have been listed in Fig. 2. The optimized calculations offer a non-planar arrangement for the ligand 5, where the TTF fragment is bent, and the two pyridine rings and the TTF unit are not on co-plane. Due to introduction of the metal ion, the conjugation of the metal complex gets an improvement when compared with the ligand 5. As shown in Fig. 2, the metal center and the TTF unit can be viewed as co-planar roughly. This arrangement provides a favorable structural feature for enhancement of electronic interaction between TTF unit and metal center.
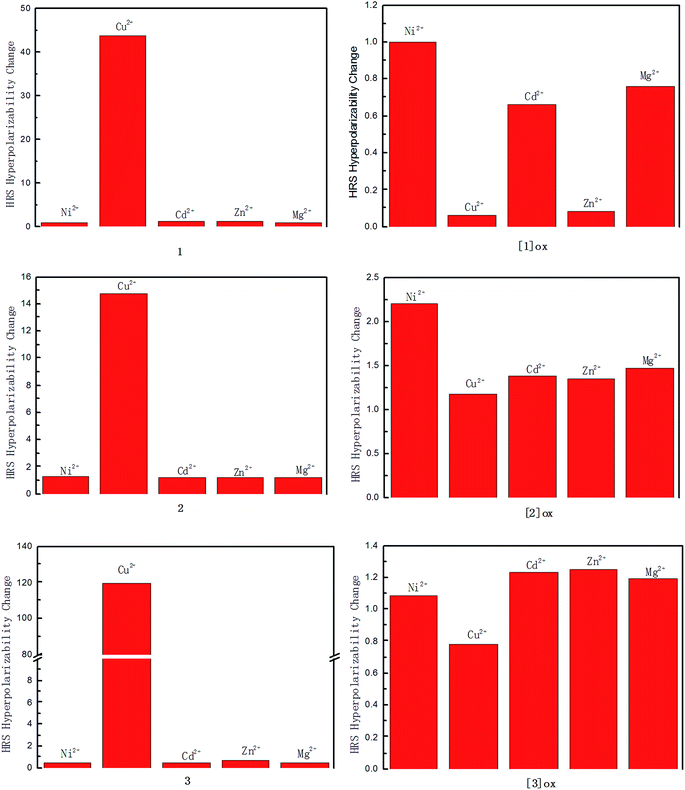
In the present paper, five kinds of metal ions, Ni2+, Cu2+, Cd2+, Mg2+, and Zn2+ have been considered as the target for detection. The dynamic first hyperpolarizability, which is closely associated with the HRS intensity, has been chosen as a source to analyze the detecting function of these exTTF and TTF derivatives. The βHRS values of all compounds studied here have been calculated at CAM-B3LYP levels using 6-31+G(d) basis sets in this work (SDD basis sets for metal atom). The calculated βHRS values have been listed in Table 1, and the HRS first hyperpolarizability change of ligands and corresponding metal complexes has been compared in Fig. 3 and 4.
| Compounds | βHRS | Compounds | βHRS |
|---|---|---|---|
| Ligand 1 | |||
| 1 | 34.44 | [1]ox | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 636.15 636.15 |
| Ni2+ | 37.41 | [Ni2+]ox | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 841.80 841.80 |
| Cu2+ | 1507.40 | [Cu2+]ox | 1376.70 |
| Cd2+ | 48.27 | [Cd2+]ox | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048.41 048.41 |
| Zn2+ | 47.92 | [Zn2+]ox | 1806.78 |
| Mg2+ | 37.04 | [Mg2+]ox | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243.70 243.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ligand 2 | |||
| 2 | 65.16 | [2]ox | 468.00 |
| Ni2+ | 83.38 | [Ni2+]ox | 1031.24 |
| Cu2+ | 962.33 | [Cu2+]ox | 549.58 |
| Cd2+ | 78.18 | [Cd2+]ox | 641.93 |
| Zn2+ | 76.53 | [Zn2+]ox | 630.86 |
| Mg2+ | 76.59 | [Mg2+]ox | 681.25 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ligand 3 | |||
| 3 | 99.18 | [3]ox | 1808.54 |
| Ni2+ | 41.17 | [Ni2+]ox | 1949.31 |
| Cu2+ | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884.8 884.8 |
[Cu2+]ox | 1413.30 |
| Cd2+ | 38.19 | [Cd2+]ox | 2229.33 |
| Zn2+ | 72.275 | [Zn2+]ox | 2252.46 |
| Mg2+ | 39.74 | [Mg2+]ox | 2153.49 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ligand 4 | |||
| 4 | 53.21 | [4]ox | 2613.80 |
| Ni2+ | 43.73 | [Ni2+]ox | 2090.41 |
| Cu2+ | 997.31 | [Cu2+]ox | 239![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.00 000.00 |
| Cd2+ | 30.49 | [Cd2+]ox | 453.71 |
| Zn2+ | 30.32 | [Zn2+]ox | 426.00 |
| Mg2+ | 28.65 | [Mg2+]ox | 425.79 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ligand 5 | |||
| 5 | 1.99 | [5]ox | 289.13 |
| Ni2+ | 3.68 | [Ni2+]ox | 331.09 |
| Cu2+ | 3102.51 | [Cu2+]ox | 1801.63 |
| Cd2+ | 18.75 | [Cd2+]ox | 2939.55 |
| Zn2+ | 19.09 | [Zn2+]ox | 2935.50 |
| Mg2+ | 26.52 | [Mg2+]ox | 3188.20 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ligand 6 | |||
| 6 | 3.77 | [6]ox | 2690.65 |
| Ni2+ | 5.52 | [Ni2+]ox | 1485.78 |
| Cu2+ | 24.17 | [Cu2+]ox | 1584.08 |
| Cd2+ | 2.42 | [Cd2+]ox | 938.14 |
| Zn2+ | 2.50 | [Zn2+]ox | 879.69 |
| Mg2+ | 2.93 | [Mg2+]ox | 1117.75 |
For the ligand 1, a substantial enhancement of the HRS first hyperpolarizability has been obtained when complexing Cu2+, which leads to a 44-fold increase of the HRS first hyperpolarizability according to our DFT calculations (see Fig. 3). By contrast, the complexation of Ni2+, Cd2+, Mg2+, and Zn2+ do not largely affect the βHRS value. The calculated βHRS values of the one-electron-oxidized species of the ligand 1 and corresponding metal complexes also have been listed Table 1. It can be found that the βHRS value of the ligand 1 gets a significant enhancement in the one-electron-oxidized process. The complexation of the five kinds of dication also modify the βHRS value of the one-electron-oxidized species [1]ox. However, the βHRS value of [1]ox is not sensitive to introduction of Ni2+, Cd2+, and Mg2+. By contrast, the complexation of Cu2+ and Zn2+ lead to a substantial decrease of the βHRS value, respectively. The calculated βHRS value of [1]ox is about 10 times as large as that of corresponding Cu(II) and Zn(II) complexes, respectively. This indicates that [1]ox has potential detecting function for Cu2+ or Zn2+, but can not distinguish a mixture containing Cu2+ and Zn2+.
In general, the first hyperpolarizability can be effectively tuned by lengthening the π-conjugated bridge in a suitable range. Thus, we have introduced the ethylene fragments into our studied system to design two new exTTF derivatives, ligands 2 and 3 (see Fig. 1). As shown in Table 1, the calculated βHRS values in the order: 1 < 2 < 3. Although the large HRS first hyperpolarizability would result in a strong signal, the detecting functional of ligands 2 and 3 can not be improve significantly when compared with the ligand 1. For the ligand 2, the complexation of Ni2+, Cd2+, Mg2+, and Zn2+ still do not largely affect the HRS first hyperpolarizability (see Fig. 3). And the complexation of Cu2+ results in a 25-fold increase of the HRS first hyperpolarizability. After the one-electron oxidization, the ligand 2 can not distinguish a mixture containing Cu2+, Cd2+, Mg2+, and Zn2+ because of the analogous magnitude of HRS first hyperpolarizability (βHRS(C.)/βHRS(L.) = 1.1–1.5), and the complexation of Ni2+ leads to a 2-fold increase of the HRS first hyperpolarizability. For the ligand 3, the complexation of Ni2+, Cd2+, Mg2+, and Zn2+ lead to a decrease in HRS first hyperpolarizability, but the difference between them is not substantial (βHRS(C.)/βHRS(L.) = 0.4–0.7). And a 119-fold increase of the HRS first hyperpolarizability has been obtained when complexing Cu2+. After the one-electron oxidization, the ligand 3 almost loses its detecting function for all five kinds of dication studied here because of the analogous magnitude of the HRS first hyperpolarizability.
Heteroaromatic compounds have attracted considerable interest because of their large second-order NLO responses. Earlier studies69–72 of heterocycle systems indicated that a decrease of the aromatic delocalization energy by the introduction of heterocycle would lead to the charge-transfer state dominated the ground state, and thus enhance the second-order NLO responses. Thus, we introduced the heteroaromatic fragment thiophene into our studied system to design another exTTF derivative, the ligand 4 (see Fig. 1). As expected, the HRS first hyperpolarizability of the ligand 4 is larger than that of the ligand 1 (see Table 1). The complexation of the Ni2+, Cd2+, Zn2+, and Mg2+ all lead to a decrease of the HRS first hyperpolarizability for the ligand 4. But the difference between them is not significant (βHRS(C.)/βHRS(L.) = 0.6–0.8). By contrast, the second-order NLO response gets a substantial enhancement when complexing Cu2+. The calculated βHRS value of the Cu(II) complex is 19 times as large as that of the ligand 4.
The calculated βHRS values of the one-electron-oxidized species of the ligand 4 ([4]ox) and corresponding metal complexes also have been compared in Fig. 4. It can be found that [4]ox still has a large second-order NLO response when complexing Cu2+. However, it is not possible to distinguish the Ni2+ owing to their analogous magnitude of HRS first hyperpolarizability (βHRS(C.)/βHRS(L.) = 0.8). The complexation of Cd2+, Zn2+, and Mg2+ still result in a decrease of the HRS first hyperpolarizability in a same range (βHRS(C.)/βHRS(L.) = 0.2), respectively. This indicates that [4]ox has potential detecting function for Cd2+, Zn2+, and Mg2+ respectively, but can not distinguish a mixture containing Cd2+, Zn2+, and Mg2+.
Due to the ligand 1 contains a furanoquinonoid spacer, the redox properties and second-order NLO responses would differ from the common TTF derivative. In the present paper, the exTTF unit has been replaced by the TTF unit to generate the ligand 5 (see Fig. 1). The calculated HRS first hyperpolarizabilities of the ligand 5 and corresponding complexes have been listed in Table 1. As expected, removal of the furanoquinonoid π-conjugated bridge leads to a decrease of the second-order NLO responses. Although the calculated βHRS value of the ligand 5 is 17 times as small as that of the ligand 1, the detecting function of the ligand 5 is prominent when compared with the ligand 1. Our DFT calculations show that introduction of five kinds of dication all enhances second-order NLO response (see Fig. 4). The calculated βHRS value is in the order Cu2+ > Mg2+ > Zn2+ > Cd2+ > Ni2+. A strong signal should be a prerequisite for detecting metal ions. Towards such goals, the ligand 5 may be a good candidate for detection of all five kinds of metal ions. The complexation of Cu2+ leads to a 1560-fold increase of the HRS first hyperpolarizability. The complexation of Mg2+ results in a 13-fold increase of the HRS first hyperpolarizability. The complexation of Cd2+ and Zn2+ lead to a 9-fold increase of the HRS first hyperpolarizability, respectively. And the complexation of Ni2+ results in a 2-fold increase of the HRS first hyperpolarizability. This indicates that the ligand 5 is an efficient sensor for every dications studied here, but it maybe lose its detecting capability for a mixture containing Cd2+ and Zn2+.
The calculated βHRS values of the one-electron-oxidized species of the ligand 5 and corresponding complexes also have been compared in Table 1 and Fig. 4. It can be found that the βHRS value of the ligand 5 gets a significant enhancement in the one-electron-oxidized process. The complexation of the five kinds of dication also increase the βHRS value of the one-electron-oxidized species [5]ox. However, the variation in the HRS first hyperpolarizability (10-fold increase) is similar when complexing Cd2+, Zn2+, and Mg2+. The complexation of Cu2+ gives rise to a 6-fold increase of the HRS first hyperpolarizability. And the complexation of Ni2+ does not largely affect the HRS first hyperpolarizability of [5]ox. This indicates that [5]ox has potential detecting function for Cu2+, Mg2+, Zn2+, and Cd2+, but can not distinguish the Ni2+ and a mixture containing Cd2+, Mg2+, and Zn2+.
It is well known that the typical organic NLO chromophore has mostly focused on the D–π–A structure. According to our previous studies, the TTF unit never displays the character of electron donor because of the bent geometrical arrangement.21,22 Thus we introduce an electron donor group (aniline group) into the ligand 5 to generate the ligand 6. The calculated HRS first hyperpolarizabilities of the ligand 6 and corresponding complexes have been compared in Table 1 and Fig. 4. Although the second-order NLO response of the ligand 6 gets a small enhancement with respect to the ligand 5, the detecting function of the ligand 6 is unsatisfied. The largest variation appears when complexing Cu2+, about 6 times as large as that of the ligand 6. And the response of Ni2+ is not significant, a ∼1.5-fold increase has been obtained according to our DFT calculations. The complexation of Cd2+, Mg2+, and Zn2+ lead to the same variation of HRS first hyperpolarizability (βHRS(C.)/βHRS(L.) = 0.6–0.8), respectively. This indicates that it is hard to distinguish the Ni2+ and a mixture containing Cd2+, Mg2+, and Zn2+.
The calculated βHRS values of the series of one-electron-oxidized species of the ligand 6 also have been compared in Table 1 and Fig. 4. Although the βHRS value of the ligand 6 gets a significant enhancement in the one-electron-oxidized process, the detecting function of [6]ox is still unsatisfied. A decrease of the βHRS value of [6]ox has been obtained when complexing all five kinds of metal dication, respectively. The complexation of Ni2+ and Cu2+ do not largely affect the HRS first hyperpolarizability (βHRS(C.)/βHRS(L.) = 0.6). And the complexation of Cd2+, Mg2+, and Zn2+ still lead to a same variation of the HRS first hyperpolarizability (βHRS(C.)/βHRS(L.) = 0.4), respectively. All results indicate that the ligand 6 is not an efficient sensor for the five kinds of dication even though a one-electron oxidization has been carried out.
3.2 TDDFT studies
On the basis of the complex sum-over-states (SOS) expression, Oudar and Chemla established a simple link between the molecular first hyperpolarizability and a low-lying energy charge transfer transition through the two-level model,73,74
 | (4) |
In order to get more insights of changes in the HRS first hyperpolarizability of the various ligands when complexing metal ions, we have performed the TDDFT calculation on the excited state of all ligands and their metal complexes. The ligand 5 and corresponding metal complexes have been chosen as examples to analyze the nature of the electronic transition. The TDDFT calculated excited energies, oscillator strengths, and associated orbital transitions of the ligand 5 and corresponding metal complexes have been listed in Table 2, and the rest of data has been listed in Tables S3–S7 (see ESI†). For the ligand 5, the TDDFT calculations show that the crucial excited state of the ligand 5 is the sixth excited state, which is formed by HOMO → LUMO + 6 and HOMO → LUMO + 10 transitions. The crucial excited state is defined as the lowest optically allowed excited state with substantial oscillator strength. These molecular orbitals associated with the crucial excited state have been listed in Fig. 5. It can be found that the HOMO of the ligand 5 mainly localizes on the TTF unit, and the LUMO + 6 and LUMO + 10 mainly delocalize over the TTF unit and one pyridine ring. Thus, these transitions would generate a weak charge transfer from the TTF unit to the pyridine ring.
| Compounds | βHRS(0) | Excited state | E (ev) | λ/nm | fos | Major contributions |
|---|---|---|---|---|---|---|
| 5 | 1.27 | 6 | 4.67 | 265.3 | 0.472 | HOMO → LUMO + 6 (47%) |
| HOMO → LUMO + 10 (12%) | ||||||
| Ni2+ | 1.79 | 22 | 4.16 | 298.1 | 0.104 | aHOMO → aLUMO + 6 (11%) |
| βHOMO → βLUMO + 8 (11%) | ||||||
| βHOMO → βLUMO + 11 (9%) | ||||||
| βHOMO − 5 → βLUMO + 2 (8%) | ||||||
| Cu2+ | 2.19 | 1 | 0.93 | 1340.3 | 0.003 | βHOMO − 2 → βLUMO (+45%) |
| βHOMO − 29 → βLUMO (+31%) | ||||||
| Cd2+ | 1.30 | 7 | 4.71 | 263.2 | 0.317 | HOMO → LUMO + 7 (+40%) |
| HOMO → LUMO + 1 (+15%) | ||||||
| Zn2+ | 1.34 | 6 | 4.70 | 263.8 | 0.397 | HOMO → LUMO + 7 (+37%) |
| HOMO → LUMO + 1 (+28%) | ||||||
| Mg2+ | 2.05 | 6 | 4.70 | 263.8 | 0.491 | HOMO → LUMO + 7 (46%) |
| HOMO → LUMO + 9 (13%) |
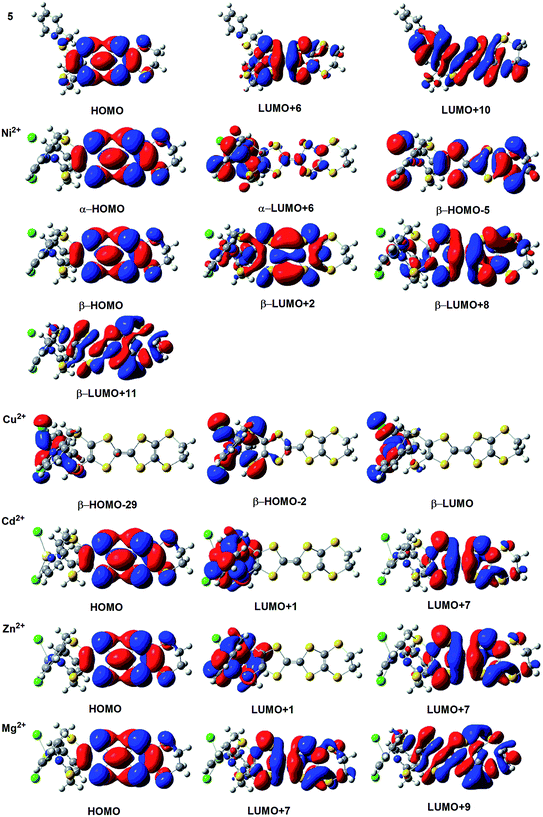 | ||
| Fig. 5 The molecular orbital associated with the crucial excited states for the ligand 5 and its metal complexes. | ||
Our TDDFT calculations show that introduction of Ni2+, Cd2+, Zn2+, and Mg2+ do not largely affect the magnitude of excited energy and oscillator strength. It is well-known that the static first hyperpolarizability is inversely proportional to the cube of excited energy and proportional to the oscillator strength, the analogous magnitudes of excited energy and oscillator strength imply small change of the static first hyperpolarizability when complexing Ni2+, Cd2+, Zn2+, and Mg2+. For the Cu(II) complex, a significant difference is obtained, where the calculated excited energy and oscillator strength of the crucial excited state get a significantly decrease. The calculated excited energy decreases to 0.93 eV (1340 nm), which is about 5 times as small as that the ligand 5. And the calculated oscillator strength decreases to 0.003 a.u., which is 157 times as small as that of the ligand 5 (we have checked the first ten excited state of the Cu(II) complex, the calculated oscillator strength is between 0.003 and 0.008. Although the oscillator strength of the first excited state is not largest among them, it has been chosen as the crucial excited state because of the very low-lying excited energy). Although the low-lying excited energy may lead to a large static first hyperpolarizability, the small oscillator strength would weaken this enhancement effect on the static first hyperpolarizability for the Cu(II) complex. In order to check the prediction by the TDDFT results, the static HRS first hyperpolarizability, βHRS(0), also has been calculated at CAM-B3LYP/6-31+G(d) level (SDD basis sets on metal atom) in this work. The calculated βHRS(0) values of the ligand 5 and corresponding metal complexes have been compared in Table 2. According to our DFT calculations, the magnitudes of the βHRS(0) for the ligand 5 and corresponding metal complexes are on the same order, ranging from 1.27 to 2.19 × 10−30 esu, which is well in agreement with our TDDFT predictions.
For the Cd(II) complex, the crucial excited state is formed by the HOMO → LUMO + 7 and HOMO → LUMO + 1 transitions. The molecular orbital associated with this crucial excited state has been listed in Fig. 5. It can be found that the HOMO still localizes on the TTF unit, and the LUMO + 7 and LUMO + 1 localize on the TTF unit, metal center, and pyridine ring. Thus these transitions would generate a charge transfer from the TTF unit to the metal center and pyridine ring, and thus this excited state contains the ligand-to-metal charge-transfer (LMCT) transition. As shown in Table 2 and Fig. 5, the crucial excited state of the Zn(II) complex also displays the nature of LMCT transition. For the Ni(II) and Mg(II) complexes, there are no contributions from the metal center for these molecular orbitals. This indicates that these excited states arise from the intraligand charge transfer (ILCT) transitions. For the Cu(II) complex, the crucial excited state composes of βHOMO − 2 → βLUMO and βHOMO − 29 → βLUMO transitions. As clearly shown in Fig. 5, these molecular orbitals are metal-based d orbital of the Cu(II) center. And thus it arises from the low-lying d–d transitions of metal center.
As shown in Fig. 4, the calculated dynamic HRS first hyperpolarizability of the Cu(II) complex for the ligand 5 is significantly larger than others. On the other hand, we have calculated the static HRS first hyperpolarizabilities of the Cu(II) complex (see Table 2). There is no significant enhancement of the βHRS(0) value when complexing Cu2+. Thus, we believe that the large dynamic HRS first hyperpolarizability of the Cu(II) complex is mainly due to the frequency dispersion effects. The SOS expression for the dynamic first hyperpolarizability tensor is
 | (5) |
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) = j − 〈0|j|0〉, Em,0 is the excited energy between the ground state and excited state m, 〈0|i|m〉 is the transition dipole between the ground state and excited state m, 〈m|i|n〉 is the transition dipole between excited states m and n, ω1 and ω2 are incident photon frequencies, and ωσ is the output photon frequency. P permutes the pairs {i, −ωσ}, {j,ω1}, {k,ω2}. The sum over permutations produce six terms. When ħωσ or ħω2 approaches Em,0, the dynamic first hyperpolarizability tensor would increase significantly. In the present paper, an incident photon frequency at 1064 nm has been chosen to calculate the dynamic HRS first hyperpolarizability. As shown in Table 2, the excited energy of the Cu(II) complex is close to the incident photon frequency, which equals to 1340 nm. We also note that the excited energy of Cu(II) complexes in ligands 1–5 are almost constant ca. 0.9 eV (ca. 1300 nm) (see ESI†), which results to a significant enhancement of the HRS first hyperpolarizability when complexing Cu2+ for ligands 1–5, which is well in agreement with our DFT calculations. As shown in Fig. 1, ligands 5 and 6 have analogous molecular structure. The calculated excited energy of the Cu(II) complex in the ligand 6 is 0.43 eV (ca. 2878 nm), which is lower than that of the ligand 5. Although the Cu(II) complex in the ligand 6 possesses a low excited energy, the enhancement of the dynamic HRS first hyperpolarizability caused by the complexation of Cu2+ is not significant when compared with the ligand 5. The dynamic HRS first hyperpolarizability of the Cu(II) complex is ∼6 times as large as that of the ligand 6 (see Fig. 4). All results indicates that the magnitude of excited energy is a very important factor in determination of the dynamic HRS first hyperpolarizability. The excited energy closed to the incident photon frequency would lead to a significant enhancement of the dynamic HRS first hyperpolarizability because of the frequency dispersion effects.
= j − 〈0|j|0〉, Em,0 is the excited energy between the ground state and excited state m, 〈0|i|m〉 is the transition dipole between the ground state and excited state m, 〈m|i|n〉 is the transition dipole between excited states m and n, ω1 and ω2 are incident photon frequencies, and ωσ is the output photon frequency. P permutes the pairs {i, −ωσ}, {j,ω1}, {k,ω2}. The sum over permutations produce six terms. When ħωσ or ħω2 approaches Em,0, the dynamic first hyperpolarizability tensor would increase significantly. In the present paper, an incident photon frequency at 1064 nm has been chosen to calculate the dynamic HRS first hyperpolarizability. As shown in Table 2, the excited energy of the Cu(II) complex is close to the incident photon frequency, which equals to 1340 nm. We also note that the excited energy of Cu(II) complexes in ligands 1–5 are almost constant ca. 0.9 eV (ca. 1300 nm) (see ESI†), which results to a significant enhancement of the HRS first hyperpolarizability when complexing Cu2+ for ligands 1–5, which is well in agreement with our DFT calculations. As shown in Fig. 1, ligands 5 and 6 have analogous molecular structure. The calculated excited energy of the Cu(II) complex in the ligand 6 is 0.43 eV (ca. 2878 nm), which is lower than that of the ligand 5. Although the Cu(II) complex in the ligand 6 possesses a low excited energy, the enhancement of the dynamic HRS first hyperpolarizability caused by the complexation of Cu2+ is not significant when compared with the ligand 5. The dynamic HRS first hyperpolarizability of the Cu(II) complex is ∼6 times as large as that of the ligand 6 (see Fig. 4). All results indicates that the magnitude of excited energy is a very important factor in determination of the dynamic HRS first hyperpolarizability. The excited energy closed to the incident photon frequency would lead to a significant enhancement of the dynamic HRS first hyperpolarizability because of the frequency dispersion effects.
4. Conclusions
In order to probe the potential detecting function for five kinds of metal ions (Ni2+, Cu2+, Mg2+, Zn2+, and Cd2+) using their second-order NLO responses, the HRS first hyperpolarizabilities of a series of exTTF and TTF derivatives have been calculated at CAM-B3LYP/6-31+G(d) levels (SDD basis sets on metal atom). The result indicates that the detecting function of these exTTF and TTF derivatives can be tuned effectively. A compound containing the simple TTF unit and chelating functional group may be an efficient sensor for all five kinds of metal ions studied here. Meanwhile, the nature of excited state also has been analyzed on the basis of the TDDFT calculations. The results indicate that introduction of Ni2+, Cd2+, Zn2+, and Mg2+ does not largely affect the magnitude of excited energy and oscillator strength. By contrast, complexation of Cu2+ leads to a significant decreases of excited energy and oscillator strength. Although the low-lying excited energy may lead to a large static first hyperpolarizability, the small oscillator strength would weaken this enhancement effect on the static first hyperpolarizability for the Cu(II) complex. The calculated static first hyperpolarizability of the ligand and its corresponding Cu(II) complex is on the same order. All results indicate that a significant enhancement of the dynamic HRS first hyperpolarizability in the Cu(II) complex is mainly due to the frequency dispersion effects.Acknowledgements
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (21373043), Chinese Postdoctoral Science Foundation (2013M540261).References
- C. Barranguet, M. Rutgers, A. M. Breure, M. Greijdanus, J. J. Sinke and W. Admiraal, Environ. Toxicol. Chem., 2003, 22, 1340–1349 CAS.
- L. K. Miao, X. F. Liu, Q. L. Fan and W. Huang, Progr. Chem., 2010, 22, 2338 CAS.
- Q. Zhou and T. M. Swager, J. Am. Chem. Soc., 1995, 117, 12593–12602 CrossRef CAS.
- M. R. Bryce, A. S. Batsanov, T. Finn, T. K. Hansen, A. J. Moore and J. A. K. Howard, Eur. J. Org. Chem., 2001, 5, 933–940 CrossRef.
- J. D. Crowley, D. A. Leigh, P. J. Lusby and R. T. A. McBurney, J. Am. Chem. Soc., 2007, 129, 15085–15090 CrossRef CAS PubMed.
- X. H. Zhou and J. C. Yan, J. Mater. Macromol., 2004, 37, 7078–7080 CrossRef CAS.
- M. R. Huang, Y. B. Ding, F. Y. Shi and X. G. Li, Progr. Chem., 2010, 24, 2224–2233 Search PubMed.
- H. Stephan, C. Koen and P. Zoe, Chem. Phys. Lett., 1996, 258, 485–489 CrossRef.
- T. Verbiest, K. Clays and V. Rodriguez, Nano Lett., 2009, 9, 3945–3948 CrossRef PubMed.
- P. Skabara, Chem. Soc. Rev., 2005, 34, 69–98 RSC.
- J. Becher, J. O. Jeppesen and K. Nielsen, Synth. Met., 2003, 309, 133–134 Search PubMed.
- M. Sliwa, A. Spangenberg, I. Malfant, P. G. Lacroix, R. B. Pansu and K. Nakatani, Chem. Mater., 2008, 20, 4062–4068 CrossRef CAS.
- J. L. Segura and N. Martín, Angew. Chem., Int. Ed., 2001, 40, 1372–1409 CrossRef CAS.
- Y. Kim, R. C. Johnson and J. T. Hupp, Nano Lett., 2001, 1, 165–167 CrossRef CAS.
- G. K. Darbha, A. K. Singh, U. S. Rai, E. Yu, H. Yu and P. C. Ray, J. Am. Chem. Soc., 2008, 130, 8038–8043 CrossRef CAS PubMed.
- V. Barone, R. Improta and N. Rega, Acc. Chem. Res., 2008, 41, 605–616 CrossRef CAS PubMed.
- D. Stefan, L. D. Franck, S. Marc, N. Antonia and D. Silvio, Org. Lett., 2007, 9, 3753–3756 CrossRef PubMed.
- B. Valeur and I. C. Leray, Chem. Rev., 2000, 205, 3–40 CAS.
- Y. L. Si and G. C. Yang, J. Phys. Chem. A, 2014, 118, 1094–1102 CrossRef CAS PubMed.
- C. G. Liu, W. Guan, P. Song, L. K. Yan and Z. M. Su, Inorg. Chem., 2009, 48, 6548–6554 CrossRef CAS PubMed.
- C. G. Liu, X. H. Guan and Z. M. Su, J. Phys. Chem. C, 2011, 115, 6024–6032 CAS.
- C. G. Liu, Z. M. Su, X. H. Guan and S. Muhammad, J. Phys. Chem. C, 2011, 115, 23946–23954 CAS.
- C. G. Liu, W. Guan, P. Song, Z. M. Su and C. Yao, Inorg. Chem., 2009, 48, 8115–8119 CrossRef CAS PubMed.
- C. G. Liu and X. H. Guan, Phys. Chem. Chem. Phys., 2012, 14, 5297–5306 RSC.
- C. G. Liu, W. Guan, L. K. Yan, Z. M. Su and P. Song, J. Phys. Chem. C, 2009, 113, 19672–19676 CAS.
- D. Roberto and R. Ugo, Organometallics, 2000, 19, 1775–1788 CrossRef CAS.
- J. L. Lyskawa, F. Le Derf, E. Levillain, M. Mazari and M. Sallé, Eur. J. Org. Chem., 2006, 10, 2322–2328 CrossRef PubMed.
- J. Lyskawa, M. Ocüafrain, G. Trippé, F. Le Derf, M. Sallé, P. Viel and S. Palacin, Tetrahedron, 2006, 62, 4419–4425 CrossRef CAS PubMed.
- S. Silvi, A. Arduini, A. Pochini and A. Secchi, J. Am. Chem. Soc., 2007, 129, 13378–13379 CrossRef CAS PubMed.
- D. R. Kanis, M. A. Ratner and T. Marks, Chem. Rev., 1994, 94, 195–242 CrossRef CAS.
- A. Datta, S. S. Mallajosyula and S. K. Pati, Acc. Chem. Res., 2007, 40, 213–221 CrossRef CAS PubMed.
- P. Innocenzi and B. Lebeau, J. Mater. Chem., 2005, 15, 3821–3831 RSC.
- M. M. Ayhan, A. Singh, C. Hirel, A. G. Gürek, V. Ahsen, E. Jenneau, I. Ledoux-Rak, J. Zyss, C. Andraud and Y. Bretonnieère, J. Am. Chem. Soc., 2012, 134, 3655–3658 CrossRef CAS PubMed.
- B. J. Coe, K. Clays, S. Foerier, T. Verbiest and I. Asselberghs, J. Am. Chem. Soc., 2008, 130, 3286–3287 CrossRef PubMed.
- A. Valore, E. Cariati, S. Righetto, D. Roberto, F. Tessore, R. Ugo, I. L. Fragalá, M. E. Fragalá, G. Malandrino, F. D. Angelis, L. Belpassi, I. Ledoux-Rad, K. H. Thi and J. Zyss, J. Am. Chem. Soc., 2010, 132, 4966–4970 CrossRef CAS PubMed.
- H. M. Kima and B. R. Cho, J. Mater. Chem., 2009, 19, 7402–7409 RSC.
- B. J. Coe, J. L. Harries, M. Helliwell, L. A. Jones, I. Asselberghs, K. Clays, B. S. Brunschwig, J. A. Harris, J. Garin and J. Orduna, J. Am. Chem. Soc., 2006, 128, 12192–12204 CrossRef CAS PubMed.
- S. Barlow, H. E. Bunting, C. Ringham, J. C. Green, G. U. Bublitz, S. G. Boxer, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 1999, 121, 3715–3723 CrossRef CAS.
- M. Quintiliani, J. Pérez-Moreno, I. Asselberghs, P. Vázquez, K. Clays and T. Torres, J. Phys. Chem. B, 2010, 114, 6309–6315 CrossRef CAS PubMed.
- C. Dhenaut, I. Ledoux, I. D. W. Samuel, J. Zyss, M. Bourgault and H. Le Bozec, Nature, 1995, 374, 339–342 CrossRef CAS PubMed.
- C. Lee, W. T. Yang and R. G. Parr, Phys. Rev., 1988, 37, 785–789 CAS.
- M. Torrent-Succarat, M. Sola, M. Duran, J. M. Luis and B. Kirtman, J. Chem. Phys., 2004, 120, 6346–6352 CrossRef PubMed.
- I. D. L. Albert, J. O. Morley and D. Pugh, J. Phys. Chem., 1997, 101, 1763–1766 CrossRef CAS.
- C. R. Moylan, S. Ermer, S. M. Lovejoy, I. H. McComb, D. S. Leung, R. Wortmann, P. Krdmer and R. J. Twieg, J. Am. Chem. Soc., 1996, 118, 12950–12955 CrossRef CAS.
- P. Fischer and F. Hache, Chirality, 2005, 17, 421–437 CrossRef CAS PubMed.
- O. Maury and L. H. Bozec, Acc. Chem. Res., 2005, 38, 691–704 CrossRef CAS PubMed.
- S. Keinan, M. J. Therien, D. N. Beratan and W. Yang, J. Phys. Chem. A, 2008, 112, 12203–12207 CrossRef CAS PubMed.
- B. Valeur and I. C. Leray, Chem. Rev., 2000, 205, 3–40 CAS.
- G. K. Darbha, A. K. Singh, U. S. Rai, E. Yu, H. Yu and P. C. Ray, J. Am. Chem. Soc., 2008, 130, 8038–8043 CrossRef CAS PubMed.
- Y. P. Zhao, L. Z. Wu, G. Si, Y. Liu, H. Xue, L. P. Zhang and C. H. Tung, J. Org. Chem., 2007, 72, 3632–3639 CrossRef CAS PubMed.
- D. Stefan, X. L. Shi, L. D. Franck, N. Antonia and D. Silvio, Org. Lett., 2007, 9, 3753–3756 CrossRef PubMed.
- A. D. Becke, Phys. Rev., 1993, 98, 5648–5652 CAS.
- A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650–7657 CrossRef CAS PubMed.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- B. Champagne, A. Plaquet, J. C. Pozzo, V. Rodriguez and F. Castet, J. Am. Chem. Soc., 2012, 134, 8101–8103 CrossRef CAS PubMed.
- B. Kirtman, B. Champagne and D. M. Bishop, J. Am. Chem. Soc., 2000, 122, 8007–8012 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, J. Chem. Phys., 1996, 100, 12974–12980 CrossRef CAS.
- D. Qi, Y. Zhang, L. Zhang and J. Jiang, J. Phys. Chem. A, 2010, 114, 1931–1938 CrossRef CAS PubMed.
- D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS.
- E. A. Perpète, D. Jacquemin, C. Adamo and G. E. Scuseria, Chem. Phys. Lett., 2008, 456, 101–104 CrossRef PubMed.
- D. Jacquemin, E. A. Perpeète, G. E. Scuseria, I. Ciofini and C. Adamo, Chem. Phys. Lett., 2008, 465, 226–229 CrossRef CAS PubMed.
- M. de Wergifosse and B. Champagne, J. Chem. Phys., 2011, 134, 074113 CrossRef PubMed.
- R. Zalesśny, I. W. Bulik, W. Bartkowiak, J. M. Luis, A. Avramopoulos, M. G. Papadopoulos and P. Krawczyk, J. Chem. Phys., 2010, 133, 244308 CrossRef PubMed.
- T. H. J. Dunning and P. J. Hay, Modern Theoretical Chemistry, ed. H. F. Schaefer III, 1976, vol. 3, pp. 1–28 Search PubMed.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- P. R. Varanasi, A. K.-Y. Jen, J. Chandrasekhar, I. N. N. Namboothiri and A. Rathna, J. Am. Chem. Soc., 1996, 118, 12443–12448 CrossRef.
- I. D. L. Albert, T. J. Marks and M. A. Ratner, J. Am. Chem. Soc., 1997, 119, 6575–6582 CrossRef CAS.
- I. D. L. Albert, T. J. Marks and M. A. Ratner, Chem. Mater., 1998, 10, 753–762 CrossRef CAS.
- E. M. Breitung, C. F. Shu and R. J. McMahon, J. Am. Chem. Soc., 2000, 122, 1154–1160 CrossRef CAS.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS PubMed.
- J. L. Oudar, J. Chem. Phys., 1977, 67, 446–457 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The dynamic HRS first hyperpolarizability of the ligand 5 calculated by various basis sets, average bond length of the key bond and dihedral angles of experimental and the calculated parameters for an Ni(II) complex, the static HRS first hyperpolarizability (βHRS(0)) and TDDFT result for the ligand 1–4, and 6 and there corresponding metal complexes, and the optimized coordinates of the ligand 5 and its metal complexes. See DOI: 10.1039/c5ra00554j |
| This journal is © The Royal Society of Chemistry 2015 |