Analysis of bioactive constituents of saffron using ultrasonic assisted emulsification microextraction combined with high-performance liquid chromatography with diode array detector: a chemometric study†
Abstract
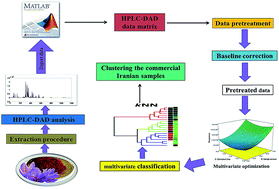
In recent years, there has been an increasing interest in the analysis of the major active components of saffron owing to their significant role in various industries, such as food, medicine and perfume. In other words, analysis of the major active components of saffron can give complete information about its chemical composition, which can be used as a reliable index for the quality control of different saffron samples (i.e., natural and commercial). The aim of the present work was to develop a simple, low cost, efficient and comprehensive strategy for the extraction and analysis of the bioactive components of saffron. In this regard, ultrasonic-assisted solvent extraction (UASE) combined with ultrasonic-assisted emulsification microextraction (USAEME) is proposed for the extraction and preconcentration of the bioactive constituents of saffron. The extracted components are then analyzed using reverse-phase high-performance liquid chromatography with diode array detector (RP-HPLC-DAD). The effective parameters on the efficiency of extraction procedure are optimized using multivariate chemometric techniques. As a consequence, the optimum extraction parameters were 79.6 mg of a saffron sample, 1.1 mL of the extraction solvent (water), 62.7 μL of the preconcentration solvent (chloroform) and 18.6 min sonication time. In optimum extraction conditions, the relative standard deviations (RSDs) were below 1.0% (n = 3) for all the components. Moreover, the enrichment factors were higher than 10 for most components. Finally, the developed analytical method is used as a reliable method for the quality control of fifteen commercial saffron samples purchased from different markets. To do this, two multivariate clustering methods, principal component analysis (PCA) and k-means, are used for determining similarities and dissimilarities between standard and commercial saffron samples, according to their HPLC fingerprints. It is concluded that the proposed method is a fast, simple, accurate and unbiased method for analyzing the bioactive components of saffron and fingerprinting commercial saffron samples, obtaining a more complete set of information from data than conventional methods.

 Please wait while we load your content...
Please wait while we load your content...