Band engineering and charge separation in the Mo_1−xW_xS₂/TiO₂ heterostructure by alloying: first principle prediction

Abstract

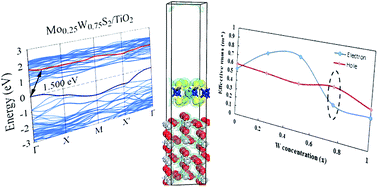
The composition dependent electronic properties of the Mo_1−xW_xS₂ monolayer deposited over a TiO₂ (110) substrate were investigated based on ab initio density functional calculations by applying periodic boundary conditions. Adsorption of the Mo_1−xW_xS₂ monolayer on the TiO₂ is physical in nature based on calculated binding energy values. It was found that the mechanical strain generated by the presence of TiO₂ beneath the Mo_1−xW_xS₂ layer resulted in a shift in band position of the Mo_1−xW_xS₂ in favor of photoelectrochemical water splitting. Moreover, variation of W concentration in Mo_1−xW_xS₂ could improve the charge separation and increase the effective mass ratio leading to an extension of the electron–hole pair lifetime which is useful for photocatalytic and photoelectrochemical applications.

---

1. Introduction

Several years after the pioneering work of Fujishima and Honda¹ on the water splitting reaction at photoinduced titanium dioxide crystals, efforts to improve the properties of TiO₂ and other photocatalysts have remained an important issue. TiO₂, as a wide band gap semiconductor, is one of the most attractive photocatalysis and photovoltaic materials that has been investigated for solar energy conversion, as well as water and air purification, extensively.² Under ultraviolet irradiation (<387 nm), whose energy exceeds the band gap of 3.3 eV in the anatase crystalline phase, TiO₂ is highly active and chemically stable. Efforts to reduce the band gap energy of TiO₂ have been carried out by many researchers in the last few decades.^3–8 In fact a high performance photocatalyst should absorb visible light (>400 nm) which is the main part of the solar spectrum.

It is well established that there are several methods for modifying TiO₂: (1) metal ion doped TiO₂ using transition metals such as: Cu,⁹ Co,¹⁰ Ni and Cr,¹¹ Fe,¹² Pt^13,14 (2) reduced TiO_x photocatalysts, (3) nonmetal doped TiO₂ (N, S, C, B, P, I, F),¹⁵ (4) composites of TiO₂ with semiconductor having lower band gap energy (e.g. CdS particles¹⁶), (5) sensitizing of TiO₂ with dyes (e.g. thionine¹⁷) and (6) TiO₂ doped with up conversion luminescence agent.¹⁸ Nevertheless, the doping method can alter the visible light photocatalytic efficiency of TiO₂ to some extent, thus the photocatalytic performance is still restricted by the relatively high recombination rate of electron–hole pairs.^19,20 This challenge must be resolved by using appropriate strategy. Recently, property of TiO₂ composites semiconductors have been modified using 2D transition metal dichalcogenides (TMD) for visible light applications. For instance, the MoS₂/TiO₂ composite exhibits a great improvement in photocatalytic hydrogen production^21–24 and dye degradation under visible light illumination.²⁵

Generally a decent candidate semiconductor for photoelectrochemical water splitting should meet three requirements simultaneously. First, to supply the driving force of the kinetics of the hydrogen and oxygen evolution reactions, that needs a semiconductor with band gap energy of at least 1.6–1.7 eV. Second, the band offsets must straddle the redox potentials of water. Finally, the semiconductor should be stable in an aqueous solution.²⁶ Transition metal dichalcogenides materials can meet the above requirements.²⁷

Bulk TMD is layered materials in which the interaction forces between layers are van der Waals forces in nature, like graphene and hexagonal boron nitride (h-BN) layers. These two dimensional (2D) semiconductor materials have attracted great attention due to their suitability of energy band gaps which match the solar spectrum from 0.89 to 1.87 eV, leading to high absorption of a significant percentage of the visible light, thus such 2D materials have great potential implications in high effective solar energy conversion, such as photoelectrochemical water splitting.

The nanosized MoS₂ in the MoS₂/TiO₂ composite plays as photosensitizer role, which can absorb visible light and transfer photoexcited electrons from MoS₂ to TiO₂,²⁷ and thus it can enhance the charge separation and restrain the recombination of the photoinduced electron and hole carriers in TiO₂.²⁸ Based on King et al.²⁷ work, it was shown that low charge carrier mobility and low absorbed light limit the photocurrent efficiency of the MoS₂/TiO₂ composites. Moreover, the band edge position of conduction band (CB) and valance band (VB) of the MoS₂ with respect to the water redox potentials is another limitation for MoS₂ as an efficient photocatalyst for water splitting reaction. Indeed, the valance band maximum (VBM) should be located at a more positively potential than the oxygen reduction potential (O₂/H₂O) while the CB should be positioned more negatively than the proton reduction potential (H⁺/H₂). Since the band gap of single layer MoS₂ is significantly influenced by mechanical strain, it is important to study the changes in band edge potentials under strain.²⁹ Thus, modification of MoS₂ electronic structure with a suitable material is an important process for achieving a better photoelectrochemical activity. Alloying of monolayer TMD semiconductors could extend the unique electronic properties of composite semiconductors. Xi et al.³⁰ have shown that band gap of atomically thin MoS₂ is tunable by alloying with W. The free energy of mixing is negative for these monolayer alloys, indicating that they are thermodynamically stable at the room temperature.

Controlling the composition of MoS₂ alloys is promising for band gap engineering and modulating their electronic properties like electron and hole mobility³⁰ as well as optoelectronic properties.^30,31 Several works have theoretically investigated photocatalytic properties of TMD,^32,33 and their alloys³⁰ as well as composites with other semiconductors like TiO₂³⁴ with short description. However, to the best of our knowledge, there is no any published report on electronic structure of the hybrid TMD alloys on TiO₂. In this study, we investigate the role of TiO₂ substrate by considering its generated strain effect on Mo_1−xW_xS₂ as well as the nature of their interface on the electronic property of the system using density functional theory with periodic boundary conditions and considering all electrons. From technological view point, studying the electronic structures of compositionally controlled Mo_1−xW_xS₂ interfaced with TiO₂ underlayer is essential to tune optoelectronic properties of the system for photocatalytic and photoelectrochemical applications.

2. Computational methods

First principle calculations were carried out by Dmol3 package using density functional theory (DFT). Besides, we have used the Perdew–Burke–Ernzerhof (PBE) pseudo-potential³⁵ along with the generalized gradient approximation (GGA) as an exchange correlation functional. The all electron (AE) core treatment and double numeric plus polarization (DNP) basis set are utilized for the spin-polarized DFT calculations. In our calculation, a vacuum region equals to 18 Å is applied to prevent the interaction between neighboring cells in the direction normal to the Mo_1−xW_xS₂ surface. The energy of this structure is optimized by an iterative method, in which the coordinates are modulated, so that the energy of the structure is brought to a stationary point, i.e., one in which the change in energy in successive iterations is less than 1.0 × 10⁻⁵ Ha (1 Ha = 27.2114 eV). In addition, the geometry optimizations were carried out until the forces on each atom during the structure relaxation were reduced below 0.002 Ha/Å and the maximum displacement was reached to 0.005 Å.

The structure of a monolayer of Mo_1−xW_xS₂ sheet is shown in Fig. 1. To model a TiO₂ substrate with the Mo_1−xW_xS₂ surface layer, one √3 × 2 rectangular monolayer of Mo_1−xW_xS₂ was placed on the top of four layer 2 × 1 rutile (tetragonal, P4₂/mnm) TiO₂ (110) slab. The monolayer of the Mo_1−xW_xS₂ considered hexagonal lattice with honeycomb structure (1H–Mo_1−xW_xS₂) similar to graphene.³⁴ Many possible configurations can be formed in TMD alloys, but the alloys with atoms being randomly distributed become more stable due to higher entropy according to Wei et al.³⁶ work showing randomly constructed Mo_1−xW_xS₂ is the stable phase.

Fig. 1 (a) The unit cell of rutile TiO₂, (b) the top view of monolayer MoS₂ sheet and (c) the side view of the four-layer rutile TiO₂ (110) slab, (d) the top view of the √3 × 2 rectangular monolayer Mo_1−xW_xS₂ sheet.

Brillouin zone sampling was conducted with Monkhorst-Pack (MP) special k point meshes. Sufficient dense k-point mesh is needed for integration over the irreducible Brillouin zone to simulate optical transitions. For all calculations, the k-point sampling is set 6 × 6 × 1 for optimization and 8 × 8 × 1 for adsorption energy and density of states (DOS) as well as band structure calculations. Note that increasing the k-point sampling to larger numbers, the changes in adsorption energy of molecule, binding energy between Mo_1−xW_xS₂ and the substrate, and band gap were only less than 0.1%, 0.1% and 3.6%, respectively. Therefore, these low values do not affect computational accuracy.

3. Results and discussion

3.1 Geometric structure

After relaxation, we have found that the oxygen atoms located on the top surface of the TiO₂ and the oxygen terminated substrate interfaced with the Mo_1−xW_xS₂ monolayer as shown in Fig. 2. To study the electronic properties of the Mo_1−xW_xS₂/TiO₂ (110) heterostructures, it is indispensable to study the geometric and electronic structure of MoS₂, WS₂ and TiO₂ separately.

Fig. 2 Optimized geometry of the interface between Mo_1−xW_xS₂ and rutile TiO₂ (110) surface (a) top view (b) side view. Red, light gray, yellow, and cyan balls represent O, Ti, S, and Mo, respectively.

Therefore, the Mo_1−xW_xS₂ systems have been optimized geometrically (see sections S2 and S3, ESI†) and their band structures obtained based on PBE/GGA approach. According to our data analysis, band gap of the Mo_1−xW_xS₂ systems with different x values was calculated and results are shown in Fig. 3. Band gap energies of 1.810, 1.816, 1.831 and 1.833 eV were obtained for the MoS₂, Mo_0.75W_0.25S₂, Mo_0.5W_0.5S₂, Mo_0.25W_0.75S₂ and WS₂. The computed results are in good agreement with experimental as well as other reported theoretical values.^31,37,38 Table 1 shows a summary of reported band gap values obtained by different methods. The difference in tabulated values originates from implication of different exchange correlation functionals. It should be noted that the calculated band gap of the pure TiO₂ is always under estimated by GGA approach.³⁹

Fig. 3 The PBE calculated band structures of the Mo_1−xW_xS₂ systems along high symmetry lines of the Brillouin zone.

Table 1 The calculated and experimental band gap energy of a single layer of Mo_1−xW_xS₂ system

Structure	Method	Band gap (eV)	Ref.
MoS2	Experimental	1.9	36
MoS2	GGA	1.7	35
	HSE06	2.10
MoS2	GGA	0.79	48
WS2		0.82
WS2	GGA	1.5	36
	HSE	1.9
MoS2	LDA	1.71	29
WS2	LDA	1.67
MoS2	GGA	1.67	33
	HSE	2.14
WS2	GGA	1.81
	HSE	2.30
MoS2	GGA	1.81	This work
WS2	GGA	1.86	This work
Mo0.5W0.5S2	GGA	1.8	30
Mo0.5W0.5S2	GGA	1.831	This work

---

In order to understand the role of addition of W concentration on property and function of the Mo_1−xW_xS₂/TiO₂ (110) structure, different values of x were examined under similar conditions and as a result the Mo_1−xW_xS₂/TiO₂ (110) heterojunctions were geometrically optimized, and the most stable geometry was identified by minimizing the total energy. As seen in Fig. 2, the two S atoms located in the bottom layer of the Mo_1−xW_xS₂ sheet adsorbed on the bridge sites of the O atom on the surface of TiO₂ (110) slab. Moreover, electron density has been calculated for all Mo_1−xW_xS₂/TiO₂ (110) structures. The existence of electron density overlap between Mo_1−xW_xS₂ and TiO₂ (110) is confirming that the interaction can occur between the structures. Furthermore, we have also calculated the distance between heterojunctions (D_z), as listed in Table 2. Based on the obtained results, a longer bond distance indicating that the interaction between Mo_1−xW_xS₂ and TiO₂ (110) is fairly weak.

Table 2 Adsorption properties, distances, band gaps, potential build up and effective mass relative ratio (D) within the PBE exchange and correlation functional of monolayer Mo_1−xW_xS₂ Sheets on rutile TiO₂ (110) Slabs

Structure	Ebinding (eV)	Dz (Å)	Eg (eV)	Potential build up (V)
MoS2/TiO2	−0.143	3.413	1.241	0.499	1.100
Mo0.75W0.25S2/TiO2	−0.127	3.423	1.265	0.599	0.711
Mo0.5W0.5S2/TiO2	−0.110	3.431	1.415	0.675	0.639
Mo0.25W0.75S2/TiO2	−0.089	3.433	1.500	0.756	1.512
WS2/TiO2	−0.068	3.446	1.615	0.873	1.241

---

The binding energy (E_b) could explain the bond strength between the Mo_1−xW_xS₂ sheet and TiO₂ (110) slab in more precisely way. Thus it is an important quantity that must be obtained and it is defined as following:⁴⁰

E_b = E_{Mo1−xWxS2/TiO2} − (E_Mo1−xWxS2 + E_TiO2) (1)

where E_Mo1−xWxS2 and E_TiO2 are total energy of isolated Mo_1−xW_xS₂ and TiO₂ (110) structures and E_{Mo1−xWxS2/TiO2} is energy of interacted hybrid structure.

As listed in Table 2 and seen in Fig. 4, the interaction between the Mo_1−xW_xS₂ and TiO₂ (110) heterostructures is weak, so it is physical adsorption in nature. To investigate the role of addition of W in the structure with binding energy it is necessary to examine this effect. It was found that increasing the W contents in the MoS₂ leads to a weaker binding energy between Mo_xW_1−xS₂ sheet and TiO₂ (110) slab.

Fig. 4 The variation of binding energy between the Mo_1−xW_xS₂ and TiO₂ (110) as a function of W concentrations.

3.2 Charge transfer analysis

To explain the charge transfer and separation process, the three dimensional charge density difference, was calculated by subtracting the electronic charges of the pristine Mo_xW_1−xS₂ and TiO₂ (110) slab from that of the Mo_1−xW_xS₂/TiO₂ (110) heterostructures (see Fig. S1, ESI†). The charge distribution mainly occurred at the interface between Mo_1−xW_xS₂ and TiO₂ (110) and the electron transfer orientation is directed from Mo_1−xW_xS₂ to TiO₂ (110). Based on Bader analysis,⁴¹ we have calculated the amount of the charge transfer from Mo_1−xW_xS₂ to TiO₂ as following: 0.061e, 0.064e, 0.068e, 0.071e and 0.075e electrons transferred from the MoS₂, Mo_0.75W_0.25S₂, Mo_0.5W_0.5S₂, Mo_0.25W_0.75S₂ and WS₂ to TiO₂. It was found that incorporation of W into MoS₂ structure leads to partially increasing of electron transfer from Mo_1−xW_xS₂ layer to TiO₂ substrate. Projected (partial) density of states (PDOSs) for all the Mo_1−xW_xS₂/TiO₂ (110) hybrid systems was obtained based on PBE calculation and the results are presented in Fig. 5. The Fermi level was set to zero as reference point. For the PDOS of pure TiO₂, the valence band (VB) and conduction band (CB) mainly consist of O (2p) and Ti (3d) orbitals. Moreover, PDOS of the Mo_1−xW_xS₂/TiO₂ system was also computed as seen in Fig. 5. It is to note that VB is composed of Mo (4d) orbital, whereas the CB is consisted of Ti (3d) orbital. However for Mo_1−xW_xS₂/TiO₂ system the VB is composed of Mo and W (4d) orbitals, whereas the CB is primarily Ti (3d) orbitals.

Fig. 5 PDOS calculated of the Mo_1−xW_xS₂/TiO₂ (110) heterojunctions based on PBE. The Fermi level of all of these systems is displayed with a black dashed line.

Band alignment of the Mo_1−xW_xS₂/TiO₂ (110) heterojunctions is a typical type II category³⁴ where the CB of the Mo_1−xW_xS₂ is placed at higher energy state than that of the TiO₂ (110). The energy difference between the CB of both Mo_1−xW_xS₂ and TiO₂, is given in Table 2, Based on PDOS data analysis. We have found that by increasing the amount of W in the Mo_1−xW_xS₂, it widens the distance between the CB of Mo_1−xW_xS₂ and CB of TiO₂. The observed widening is due to alloying and this phenomenon was also seen and reported for the n-Zn_0.8Mg_0.2O/p-Ni_0.8Mg_0.2O very recently.⁴² Moreover, this finding is also in a good agreement with calculated amounts for binding energy that is higher for the MoS₂/TiO₂ than the WS₂/TiO₂. The energy difference between CB of the Mo_1−xW_xS₂ and CB of TiO₂ drives charge transfer phenomena between Mo_1−xW_xS₂ and TiO₂. This phenomena cause an effective charge separation leading to potential build up and consequently it lowers electron–hole recombination rate.

According to the obtained PDOS figures, the location of Ti (3d) and O (2p) orbitals did not change by varying W concentrations in the Mo_1−xW_xS₂/TiO₂ (110) hybrid system and as a result the energy gap of TiO₂ in all structures remains almost constant. Another important point is that the energy change for the Mo (4d) orbital is much higher than the S (2p) orbital in the MoS₂ which indicates that the change in energy gap in the Mo_1−xW_xS₂ structures is due to energy variation of the Mo (4d) orbital. Furthermore, increasing W content in the Mo_1−xW_xS₂ leads to an increase in energy level of the Mo (4d) orbital and as a result, the band gap energy of the overall system is increased.

Our calculated results also revealed that the energy band structures of the Mo_1−xW_xS₂ is strongly affected by presence of TiO₂ substrate as shown in Fig. 6. Band gap energy calculation based on GGA method and PBE functional are in good agreement with both experiment and other theoretical works reported recently.^29,37,43 Despite of the fact that a monolayer of Mo_1−xW_xS₂ sheets possess a direct band gap structure,^30,31,36 it will change to indirect band gap structure upon its conjunction with a TiO₂ (110) surface. This finding is of particular importance and can be attributed to the strain effect induced by TiO₂. The strain can be used to tune the electronic properties of MoS₂ and WS₂ systems.^44,45 Our results are consistent with previous theoretical study performed by Yun et al.⁴⁶ which was shown that strain makes band gap of monolayer dichalcogenides indirect. Moreover, analysis of band structure calculation indicates that the CB energy of the Mo_1−xW_xS₂ is hybridized with the CB energy of the TiO₂ (110) which facilitates photoinduced electron injection from the Mo_1−xW_xS₂ monolayer to TiO₂ (110) substrate as also reported in.²⁷ To understand correlation between binding energy and variation of band gap with W concentration, corresponding quantities were plotted. Fig. 7 shows the variation in energy gap versus W concentration between Mo_1−xW_xS₂ and TiO₂ (110). It is obvious that by increasing W concentration, the change in its energy gap decreased which means high W concentrations could sustain TiO₂ strain. This is due to the fact that the binding energy between Mo_1−xW_xS₂ and TiO₂ (110) decreased with increasing W concentration. As a result, band gap energy of Mo_1−xW_xS₂ weakly affected by TiO₂ as compared to energy build up defined as energy difference between CB of TiO₂ and CB of Mo_1−xW_xS₂ (see Table 2).

Fig. 6 The PBE calculated band structures of the Mo_1−xW_xS₂/TiO₂ (110) heterostructures along high symmetry lines of the Brillouin zone.

Fig. 7 Binding energy versus W concentration (blue diamonds); energy gap changes versus W concentration (red circles).

Since band gap energy of the Mo_1−xW_xS₂ in conjunction with TiO₂ (110) is in the range of 1.24 to 1.61 eV, thus the visible light irradiation can be absorbed by this hybrid structures and photoinduced electron from VB to CB can be injected to TiO₂ conduction band and the generated hole in the Mo_1−xW_xS₂ sheet can be transferred to the VB of TiO₂. Moreover, that addition of W atoms into MoS₂ could enhance the hole mobility.³⁰ In order to evaluate the separation and diffusion rate of photoinduced charge carriers, the relative ratio of effective electron and hole masses was calculated. From application view point, this ratio is one of the most important factors responsible for the photocatalytic activity of a semiconductor. The effective mass (m*) of the carriers could be extracted from calculated band structures and defined as:⁴⁷

where m* (m_e* and m_h*) represents the effective mass of conduction band minimum (CBM) and valance band maximum (VBM), ħ is the reduced Planck constant, and E(k) is the band dispersion function. Its value is easily attained by fitting a parabola to band structure as the wave function at k. The second derivative, , is defined as the curvature of energy band. Therefore, the effective mass is essentially related to inverse of curvature of energy band. The calculated m* values at different W concentrations are illustrated in Fig. 8 and the results are summarized in Table 2. The electron and hole effective mass of an individual configuration at different W concentration is provided using the equation. The smaller effective mass indicates the improved mobility of photoinduced carriers. The obtained results denote that both electron and hole effective masses of the WS₂/TiO₂ are lighter than those of the MoS₂/TiO₂, proposing that charge carriers are better transported in the WS₂/TiO_2. Among all the investigated Mo_1−xW_xS₂ structures, maximum electron effective mass is found for the Mo_0.25W_0.75S₂/TiO₂ system. In opposite to the electron effective mass, the hole effective mass decreased slightly with increasing W content. The higher electron effective mass makes the electron mobility slower. The relative ratio (D) of the effective masses generally is defined by the following formula:⁴⁸where the higher absolute value of D specifies the larger difference of charge carriers (electrons and holes) mobility and leads to the lower recombination rate of photoinduced electron–hole pairs. From Table 2, it can be found that the highest values of D were obtained for the Mo_0.25W_0.75S₂/TiO₂ system. Therefore, we believe attaining the higher separation of photoexcited electron–hole pairs, resulted in a better photoelectrochemical activity of the Mo_0.25W_0.75S₂/TiO₂ system.

Fig. 8 Effective masses of electrons and holes for the Mo_1−xW_xS₂/TiO₂ (110) monolayer alloys.

4. Conclusion

In summary, we have utilized density functional calculations with the generalized gradient approximation (GGA) for exchange correlation functional to explore the electronic properties of 2D Mo_1−xW_xS₂/TiO₂ heterostructures with different concentration of W. The study focused on understanding how TiO₂ activated under visible light irradiation with addition of 2D dichalcogenide alloys. The adsorption energy of the Mo_1−xW_xS₂ on TiO₂ is negative but significantly small for these monolayer alloys, indicating that the interaction between the Mo_1−xW_xS₂ and TiO₂ is physical in nature. It is found that the direct band gap semiconducting Mo_1−xW_xS₂ changed to indirect band gap semiconductor when deposited on TiO₂ (110), moreover, it was observed a displacement in thermodynamic band position of CB and VB of the Mo_1−xW_xS₂ in presence of TiO₂ (110) and by varying W concentration. It is believed that the shift in CB band position to more negative potential can be promote reduction power of and (H⁺/H₂) with respect to MoS₂ band position. Furthermore, the Mo_0.25W_0.75S₂/TiO₂ alloyed structure exhibits a higher relative effective mass ratio (D) which leads to a better charge separation and lower electron–hole recombination rate and could improve photoelectrochemical activity of the Mo_0.25W_0.75S₂/TiO₂ (110) system.

Acknowledgements

The authors wish to thank Research and Technology Council of Sharif University of Technology for financial assistance. Partial support of Iran National Science Foundation (Project: INSF-92034052) and Iran Nanotechnology Initiative Council (INIC) is greatly acknowledged.

Notes and references

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. T. Ochiai and A. Fujishima, J. Photochem. Photobiol., C, 2012, 13, 247–262.
3. M. Bayati, F. Golestani-Fard and A. Z. Moshfegh, Catal. Lett., 2010, 134, 162–168.
4. M. Bayati, A. Z. Moshfegh and F. Golestani-Fard, Appl. Surf. Sci., 2010, 256, 2903–2909.
5. W.-J. Ong, M. M. Gui, S.-P. Chai and A. R. Mohamed, RSC Adv., 2013, 3, 4505–4509.
6. W. Li, Y. Wang, H. Lin, S. I. Shah, C. Huang, D. Doren, S. A. Rykov, J. Chen and M. Barteau, Appl. Phys. Lett., 2003, 83, 4143–4145.
7. S. George, S. Pokhrel, Z. Ji, B. L. Henderson, T. Xia, L. Li, J. I. Zink, A. E. Nel and L. Mädler, J. Am. Chem. Soc., 2011, 133, 11270–11278.
8. M. Gholami, M. Qorbani, O. Moradlou, N. Naseri and A. Z. Moshfegh, RSC Adv., 2014, 4, 7838–7844.
9. P. Sangpour, F. Hashemi and A. Z. Moshfegh, J. Phys. Chem. C, 2010, 114, 13955–13961.
10. B. Sarkar, C. Pendem, L. N. S. Konathala, T. Sasaki and R. Bal, Catal. Commun., 2014, 56, 5–10.
11. L. Lu, F. Teng, S. Tapas, D. Qi, L. Wang and J. Zhang, Appl. Catal., B, 2015, 163, 9–15.
12. K. Vijayalakshmi and S. D. Jereil, J. Mater. Sci.: Mater. Electron., 2014, 5089–5094.
13. M. Anpo, Pure Appl. Chem., 2000, 72, 1787–1792.
14. L. Ye, Z. Li, L. Zhang, F. Lei and S. Lin, J. Colloid Interface Sci., 2014, 433, 156–162.
15. T. Ihara, M. Miyoshi, M. Ando, S. Sugihara and Y. Iriyama, J. Mater. Sci., 2001, 36, 4201–4207.
16. M. Qorbani, N. Naseri, O. Moradlou, R. Azimirad and A. Z. Moshfegh, Appl. Catal., B, 2015, 162, 210–216.
17. D. Chatterjee and A. Mahata, Appl. Catal., B, 2001, 33, 119–125.
18. S. Li, Y. Guo, L. Zhang, J. Wang, Y. Li, Y. Li and B. Wang, J. Power Sources, 2014, 252, 21–27.
19. J. Zhang, Y. Wu, M. Xing, S. A. K. Leghari and S. Sajjad, Energy Environ. Sci., 2010, 3, 715–726.
20. J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891.
21. C. Liu, L. Wang, Y. Tang, S. Luo, Y. Liu, S. Zhang, Y. Zeng and Y. Xu, Appl. Catal., B, 2015, 164, 1–9.
22. W. Zhou, Z. Yin, Y. Du, X. Huang, Z. Zeng, Z. Fan, H. Liu, J. Wang and H. Zhang, Small, 2013, 9, 140–147.
23. Q. Xiang, J. Yu and M. Jaroniec, J. Am. Chem. Soc., 2012, 134, 6575–6578.
24. N. Yang, Y. Liu, H. Wen, Z. Tang, H. Zhao, Y. Li and D. Wang, ACS Nano, 2013, 7, 1504–1512.
25. W. Ho, J. C. Yu, J. Lin, J. Yu and P. Li, Langmuir, 2004, 20, 5865–5869.
26. S. Cho, J. W. Jang, K. H. Lee and J. S. Lee, APL Mater., 2014, 2.
27. L. A. King, W. Zhao, M. Chhowalla, D. J. Riley and G. Eda, J. Mater. Chem. A, 2013, 1, 8935–8941.
28. M. S. Hamdy, J. Mol. Catal. A: Chem., 2014, 393, 39–46.
29. Y. Li, Y. L. Li, C. M. Araujo, W. Luo and R. Ahuja, Catal.: Sci. Technol., 2013, 3, 2214–2220.
30. J. Xi, T. Zhao, D. Wang and Z. Shuai, J. Phys. Chem. Lett., 2014, 5, 285–291.
31. Y. Chen, J. Xi, D. O. Dumcenco, Z. Liu, K. Suenaga, D. Wang, Z. Shuai, Y. S. Huang and L. Xie, ACS Nano, 2013, 7, 4610–4616.
32. H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238.
33. J. Kang, S. Tongay, J. Zhou, J. Li and J. Wu, Appl. Phys. Lett., 2013, 102, 012111–012114.
34. M. Niu, D. Cheng and D. Cao, J. Phys. Chem. C, 2014, 118, 5954–5960.
35. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
36. X. L. Wei, H. Zhang, G. C. Guo, X. B. Li, W. M. Lau and L. M. Liu, J. Mater. Chem. A, 2014, 2, 2101–2109.
37. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105.
38. A. B. Kaul, J. Mater. Res., 2014, 29, 348–361.
39. T. Mahmood, C. Cao, R. Ahmed, M. A. Saeed and M. Ahmed, J. Optoelectron. Adv. Mater., 2014, 16, 117–122.
40. T. H. Wang, Y. F. Zhu and Q. Jiang, J. Phys. Chem. C, 2013, 117, 12873–12881.
41. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21.
42. Y.-M. Guo, L.-P. Zhu, W.-Z. Niu, X.-Y. Zhang and Z.-Z. Ye, Appl. Phys. A, 2014, 1–4.
43. E. Scalise, M. Houssa, G. Pourtois, V. Afanas'ev and A. Stesmans, Nano Res., 2012, 5, 43–48.
44. H. Shi, H. Pan, Y. W. Zhang and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87.
45. L. Dong, R. R. Namburu, T. P. O'Regan, M. Dubey and A. M. Dongare, J. Mater. Sci., 2014, 49, 6762–6771.
46. W. S. Yun, S. W. Han, S. C. Hong, I. G. Kim and J. D. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85.
47. B. Lange, C. Freysoldt and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81.
48. H. Zhang, L. Liu and Z. Zhou, RSC Adv., 2012, 2, 9224–9229.

---

Footnote

† Electronic supplementary information (ESI) available: 2D profiles of charge density difference, experimental and optimized lattice constants of TiO₂ and MS₂ (M = Mo, W) and optimized atomic coordinates of Mo_1−xW_xS₂/TiO₂ (110) and Mo_1−xW_xS₂. See DOI: 10.1039/c5ra00330j

---