Thiacloprid suspension formula optimization by a response surface methodology

Abstract

A model thiacloprid 25% suspension concentrate was prepared using Tersperse2700 (X₁), AE1601 (X₂), xanthan gum (X₃) and Veegum (X₄). A response surface methodology (RSM) was used to evaluate the influences of four experimental factors on the aqueous separation ratio (R₁), centrifugal sedimentation ratio (R₂) and viscosity (R₃). The results show that the main factors influencing the three responses were X₃, X₄ and X₂ followed by X₁; moreover, several interactions were also significant. Multiple-response optimization was performed based on a desirability function, considering the minimum R₁, R₂, and R₃ as well as the financial cost. The integrated optimum conditions were X₃ = 0.24%, X₄ = 1.33%, X₂ = 0.50%, and X₁ = 2.90% (mass fraction). A verification experiment demonstrated that the optimized formula R₁, R₂, and R₃ were 1.69%, 2.63% and 257.74 mPa s with the average relative predicted value errors 7.69%, 4.18% and −1.41%, respectively. The response surface methodology is an effective approach for optimizing the suspension concentrate formula with comprehensive advantages.

---

Introduction

Suspension is a common form for many products including biomaterials, food, pharmaceuticals and paint. Its application to pesticides has also received extensive attention. An aqueous suspension concentrate (SC) is one of the most widely used types of pesticide formulation, especially for pesticides with poor water-solubility and relatively high melting points.¹ Rapid SC development is closely related to such unique advantages. Water, not an organic solvent, is the primary medium in a topical SC formula, which tends to decrease its environmental and financial costs, in contrast to an emulsion concentrate formula. In addition, the small SC particle size enhances the biological activity of the active ingredient.² However, as the particle size decreases, the specific surface area and surface energy significantly increase, which produces flocculation or agglomeration.³ Therefore, a formula with balanced properties is necessary to reduce flocculation, agglomeration and the sedimentation caused by gravitational stress.¹ The triangular diagram and orthogonal design methods are often used to simplify the optimization procedure. Orthogonal design is a classic fractional design method widely used in many domains with specially designed experiment tables;^4–6 in the triangle-coordinate method, several representative points on the triangle are selected.^7,8 Both methods can optimize the procedure and formula, where only several factors are considered. However, when the SC is composed of multiple components (often more than four), then it is difficult to use the triangular diagram and orthogonal design methods to determine the precise effect of each component if the interactions are considered.^9,10

Among experimental designs, the response surface methodology (RSM) is the most effective method for improving and optimizing experimental procedures using a series of statistical and mathematical techniques.^11–13 It is especially appropriate for analyzing and modelling multi-factor experiments because it can assess both the single and interaction effects for specific factors. In recent years, the RSM has significantly advanced in the food industry, pharmaceuticals, chemical engineering, architecture, energy sources and other fields.^14–19 However, few researchers have reported on the RSM in pesticide formulations mainly because its statistics and analyses are complicated. Thiacloprid, which is a type of neuroactive chemical modelled after nicotine, is a second neonicotinoid insecticide.²⁰ It was first developed by Bayer Crop Science and launched under the brand name Calypso.²¹ Thiacloprid is highly efficient at controlling sucking insects and chewing insects, including aphids, jassids, whiteflies, mites and weevils.^22,23 The technical material of thiacloprid describes crystals at room temperature with a white to light brown color. It includes a 136 °C melting point, relatively low water solubility (only 184 mg l⁻¹) and excellent chemical stability in water; thus, it is appropriate for constructing SC products.^1,24

As proof, a model thiacloprid SC was prepared to investigate the influence of wetting-dispersing agents and anti-settling agents on sample properties using the RSM. The physical stability, viscosity, fluidity, dispersibility, size distribution and suspensibility of the samples were measured. The strategy adopted for obtaining an optimized formula is expected to provide practical information to advance pesticide formulations.

Results and discussion

The design matrix for the proposed experiments and their corresponding output parameters are shown in Table S1 (ESI†). The 27 samples exhibited favorable fluidity and dispersibility. In addition, the suspensibility of the samples before storage was measured from 92.84% to 97.02%, which did not affect the applied performance of the suspension concentrate; thus, the suspensibility was not further optimized. The high suspensibility cannot be separated from the relationship between the small particle size and highly-efficient dispersibility. The sedimentation or floating of dispersing particles in the diluent must individually obey Stokes' law to a certain extent. As the density of the thiacloprid technical material is greater than the dispersal phase, the particles sediment in the diluents, and the settling rate positively correlates with the square of the particle size. Therefore, the settling rate was low for the 27 samples, wherein the particles were smaller than 3 μm. The average particle diameter of the 27 samples ranged from 1.51 μm to 2.50 μm. However, it should be noted that Ostwald ripening was obviously observed for most samples, especially after hot storage. Thiacloprid has 184 mg l⁻¹ water solubility at 20 °C; however, it is more soluble in water with an increase in temperature. In addition, an accelerated test was conducted at 54 ± 2 °C wherein the thermal motion of the particles was greatly accelerated, which also enhanced the Ostwald ripening. Fortunately, the suspensibility of all samples remained greater than 91%, even after hot storage (Table S1, ESI†). The aqueous separation ratios (R₁) of the tested samples ranged from 1% to 17%, and the centrifugal sedimentation ratio (R₂) ranged from 2% to 23%. A similar variance trend was observed for R₁ and R₂, but the variance trend for viscosity was somewhat discrepant. We expected to generate a preparation with R₁ and R₂ values lower than 5%; the moderate viscosity (R₃) was welcome. Therefore, the data for the three dependent variables were analyzed to obtain a formula that meets the above criteria.

Optimizing the aqueous separation ratio

A regression analysis was performed to fit the R₁ results using the Design-expert software. Linear, 2FI, quadratic and cubic polynomial equations were used to test the fitness (Table 1). The data showed that higher “Adjusted R²” and “Predicted R²” values yielded a better fit. As shown in Table 1, both the quadratic and cubic polynomial models showed favorable fitness with “Adjusted R²” and “Predicted R²” values greater than 0.9. The p-value is an index that indicates the significance of the data, and essentially yields a “Prob > F” value. The sequential p-values for the linear and quadratic polynomial models were below 0.05, which indicates significant models. The lack of fit p-value indicates whether the “lack of fit” is significant relative to the pure error. The data show that the linear and 2FI models could not fit the R₁ data; the lack of fit p-values were below 0.05. Considering the four evaluation indexes, the polynomial model best fits the data; therefore, it was used to indicate the adequacy of the fitted model. The quadratic polynomial model is described as follows.^25,26Y is the dependent variable, b₀ is the intercept, the X_i terms are the independent variables, and the b_i, b_i,j, b_i,i terms are the relative coefficients. Previous publications show that the polynomial model best fits the experimental data when interactions between the independent variables are significant.²⁷ The suspension concentrate is the type of complicated formulation for which interactions between different adjuvants are inevitable.

Table 1 Fitness of the aqueous separation ratio to different models

Model	Sequential p-value	Lack of fit p-value	Adjusted R^2	Predicted R^2
a 2FI: the two-factor interaction model.
Linear	<0.0001	0.0073	0.7648	0.7137
2FI^a	0.0899	0.0095	0.8251	0.8256
Quadratic polynomial	<0.0001	0.1951	0.9925	0.9807
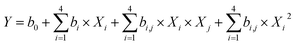Cubic polynomial	0.2484	0.2201	0.9957	0.9251

---

An analysis of variance (ANOVA) was then performed based on Fischer tests, and the corresponding p-value is listed in Table S2 (ESI†) with the regression equation coefficients. The F value is a statistical parameter of the Fischer test that indicates whether the data deviates from the mean as well as the relevance between the proposed model and experimental results. The model F-value R₁ was 248.39, which implies a significant model with only a 0.01% chance that a “Model F-value” this large could be produced from noise. Table S2† shows that X₁, X₂, X₃, X₄ and seven other terms significantly influenced R₁. The p > 0.05 indicates that the model terms were not significant. In this case, reducing the model by removing the model terms with sequential p values greater than 0.05 was the best way to improve the model.¹⁴ The prediction equation for R₁ (coded value) is described as follows.

Aqueous separation ratio (%) = 3.35 − 1.17X₁ − 1.56X₂ − 2.43X₃ − 2.62X₄ − 0.235X₁X₄ + 1.29X₂X₃ + 1.04X₃X₄ + 0.391X₁² + 0.679X₂² + 0.834X₃² + 1.49X₄² (2)

X₁, X₂, X₃ and X₄ in eqn (2) are Tersperse2700, AE1601, xanthan gum and Veegum, respectively.

The absolute value of the regression coefficients reflects the influence of each term on the responses; the positive and negative sign demonstrates that both high and low levels of the terms considered are approximately optimal. The predicted values for R₁ were generated after calculating the coded value using eqn (2). The predicted values and observed values were then regressed, as depicted in Fig. 1. The empirical equation fits well to the data and yields R² = 0.9955 (coefficient of determination). As shown in Table 2, the optimal conditions for R₁ were generated by analyzing eqn (3) using the “fmincon function” in MATLAB R2014a, and the minimal R₁ was estimated at −0.03%. Although the R₁ was favorable, the actual mass fractions of Tersperse2700 and AE1601 were slightly high, which is not economical.

Fig. 1 Measured values vs. predicted values for modelled aqueous separation ratio.

Table 2 Optimal conditions for the aqueous separation ratio

Factor	Level	Actual mass fraction/%
X1: Tersperse2700	1.92	2.96
X2: AE1601	2.00	2.50
X3: xanthan gum	−0.94	0.18
X4: Veegum	1.36	1.68

---

Response surface plots can effectively indicate interactions between dependent variables and aid in generating optimal responses with balanced conditions. With R₁ as the response, the response surface plots are shown in Fig. 2. Significant decreases in R₁ were observed with increasing levels of Tersperse2700, AE1601 and Veegum (Fig. 2a, b and d); the three other variables remained at the optimal levels. However, when their levels reached 1.0, R₁ only changed slightly. The influence of xanthan gum differed greatly, as depicted in Fig. 2c. When the level of xanthan gum was low, R₁ decreased slightly; however, at high levels of xanthan gum, R₁ increased significantly with the level of xanthan gum. Based on the above analysis, we conclude that maintaining the three variables at optimal levels and the latter variable at a moderate level yields a qualified thiacloprid 25% SC. The interactions between Tersperse2700 and Veegum, AE1601 and xanthan gum, and xanthan gum and Veegum significantly influenced R₁ when the two other variables remained at their optimal levels (Fig. 2e–g). R₁ decreased abruptly with variations in the Veegum level when the Tersperse2700 level changed; fortunately, when the Veegum quantity was maintained at the highest level, R₁ was lower than 5% (Fig. 2e). As shown in Fig. 2f, R₁ was lower than 5% when either AE1601 or xanthan gum was at its highest level. When xanthan gum was at a low level, the R₁ decreased more or less. However, when high levels of xanthan gum were added, the phenomena differed greatly. A slight increase in R₁ was observed when the Veegum level varied from 0 to 2 (coded value).

Fig. 2 Response surface plots for the aqueous separation ratio.

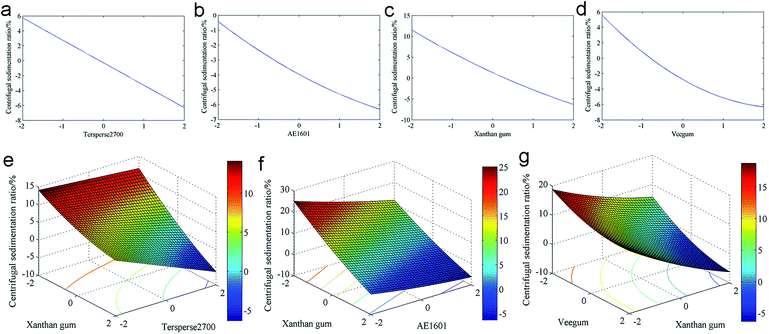
Centrifugal sedimentation ratio optimization

The centrifugal sedimentation ratio (R₂) regression analysis results are shown in Table S3 (ESI†). The four models exhibited “Adjusted R²” and “Predicted R²” values greater than 0.95, which implies favorable fitness. However, a sequential p > 0.05 was observed for the cubic polynomial model, which indicates insignificant models; however, the linear, 2FI and quadratic polynomial models were all significant. The lack of fit p-values for the linear and 2FI models was lower than 0.05, which indicates a large experimental error. Therefore, the polynomial model was the best model for fitting the R₂ results. An ANOVA was used to indicate the adequacy of the fitted polynomial model; the results are shown in Table S4 (ESI†). The model F-value was 940.72, which indicates a favorable explanation of the adopted model. Considering the p-values of the factors in Table S4,† X₁, X₂, X₃, X₄, X₁X₃, X₂X₃, X₃X₄, X₂², X₃² and X₄² are all significant model terms for R₂. The model terms with sequential p-values higher than 0.05 were removed to improve the predicted model, which yielded the following empirical equation:

Centrifugal sedimentation ratio (%) = 11.6 − 1.83X₁ − 2.43X₂ − 3.65X₃ − 2.39X₄ − 0.589X₁X₃ + 0.483X₂X₃ − 0.294X₃X₄ + 0.153X₂² + 0.324X₃² + 0.605X₄² (3)

The predicted R₂ values were generated after calculating the coded values using eqn (3). The predicted R₂ values were then regressed using the observed values, as illustrated in Fig. S1 (ESI†). The empirical equation fit well to the experimental data (R² = 0.9987). Using eqn (3), we deduced that R₂ decreased with the mass fraction of the four adjuvants. Furthermore, the minimum was estimated at −6.30% when the adjuvant doses reached the highest level. R₂ cannot be negative. In this case, the emphasis on generating the lowest R₂ through maintaining the variables at their highest level was a wasted effort.

To clearly investigate the influence of the four factors on R₂, the response surfaces were plotted. First, three variables were maintained at their optimal levels, and the other variable ranged from −2.0 to 2.0 (coded value) to discern the influence of that variable. As illustrated in Fig. 3a, significant decreases were observed for R₂ with increasing levels of Tersperse2700. The singular influences from AE1601, xanthan gum and Veegum exhibited the same trend, as depicted in Fig. 3b–d. However, as indicated from eqn (3), the optimal levels of the three constant variables were the highest levels. Furthermore, maintaining the latter variable at a high level would cause equipment damage because this experiment would be performed at extreme conditions. The interactions between Tersperse2700 and xanthan gum, AE1601 and xanthan gum, xanthan gum and Veegum exhibited significant influences on R₂. As depicted in Fig. 3f, the R₂ decreased significantly with the AE1601 and xanthan gum levels when the other two variables were maintained at an optimal level (also the highest level, 2.0). A similar trend was observed for the interactions between Tersperse2700 and xanthan gum (Fig. 3e) as well as xanthan gum and Veegum (Fig. 3g).

Fig. 3 Response surface plots for the centrifugal sedimentation ratio.

Viscosity optimization

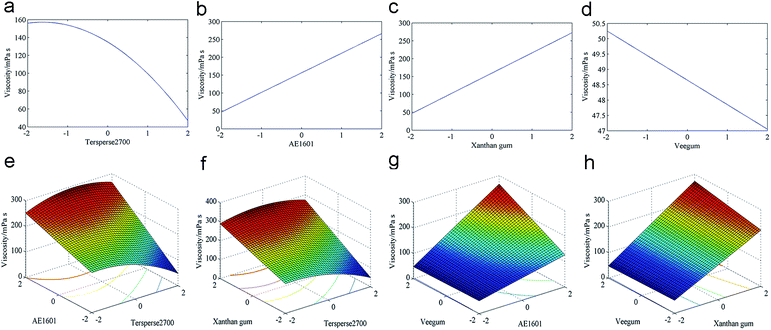
The viscosity regression analysis results are shown in Table S5 (ESI†). The cubic polynomial model yielded a sequential p-value greater than 0.05, which implies that the model is insignificant. Furthermore, the linear model could not fit the viscosity results based on a significant “Lack of fit”. Both the 2FI and quadratic polynomial models were appropriate for fitting the viscosity results. However, the quadratic polynomial model exhibited a lower “Lack of fit”, therefore it was more suitable for fitting the viscosity results.

The ANOVA was used to indicate the adequacy of the fitted polynomial model; the results are shown in Table S6 (ESI†). The model F-value was 112.04, which indicates a significant model with only a 0.01% chance that a “Model F-value” this large could be due to noise. Based on the sequential p-values in Table S5,† X₂, X₃, X₄, X₁X₂, X₁X₃, X₂X₄, X₃X₄ and X₁² are significant model terms for viscosity. The model terms with sequential p > 0.05 were removed to improve the predicted model, which yielded the following empirical equation.

Viscosity (mPa s) = 254 + 21.3X₂ + 37.6X₃ + 24.3X₄ + 7.76X₁X₂ + 5.86X₁X₃ + 9.01X₂X₄ + 3.55X₃X₄ − 8.36X₁² (4)

The predicted viscosity values were obtained after calculating the coded value using eqn (4). Next, the predicted and observed values were regressed, as shown in Fig. S2 (ESI†). The empirical equation fit well to the data (R² = 0.9841). The minimal viscosity could be estimated using the “fmincon function” of MATLAB R2014a. Using eqn (4), the optimal conditions for minimal viscosity are determined as X₁ = 2.00, X₂ = −2.00, X₃ = −2.00 and X₄ = 2.00, and the minimum was estimated at 47.05 mPa s. However, the optimal conditions for minimal viscosity were inconsistent with favorable physical stability. Next, the response surfaces were plotted to discern the influence of the independent variables on viscosity.

When the Tersperse2700 was low, the viscosity of the preparation changed slightly. However, the viscosity decreased abruptly when the Tersperse2700 amount exceeded 0 (Fig. 4a). A significant increase of the viscosity was observed with an increase in either the AE1601 or xanthan gum level, as illustrated in Fig. 4b and c. Although the viscosity decreased significantly with the Veegum level, only a slight decrease in viscosity was observed (Fig. 4d). For the significant interactions, a similar trend in viscosity variations was observed for the interactions between Tersperse2700 and AE1601 (Fig. 4e) as well as Tersperse2700 and xanthan gum (Fig. 4f). The viscosity increased abruptly with the AE1601 level regardless of the Tersperse2700 quantity added, as shown in Fig. 4e. The Tersperse2700 influence differed greatly. When AE1601 was maintained at the lowest level, the viscosity decreased more or less with an increasing level of Tersperse2700. However, opposite results were observed when AE1601 was maintained at its highest level (Fig. 4f). The Veegum quantity barely influenced the viscosity when the AE1601 was maintained at a low level; however, the viscosity significantly increased with the Veegum level when high levels of AE1601 were added (Fig. 4g). As illustrated in Fig. 4h, a significant change in viscosity was not observed with varying levels of Veegum regardless of the xanthan gum quantity applied. However, the viscosity increased in an approximately linear manner with the xanthan level. Thus, we conclude that maintaining Tersperse2700 at a high level as well as maintaining AE1601 and xanthan gum at low levels is highly beneficial for producing SC samples with low viscosity, but the Veegum level is not important.

Fig. 4 Response surface plots for viscosity.

Multiple-response optimization

The most important goal for applying RSM is process optimization. Herein, the three individual responses were the aqueous separation ratio, centrifugal sedimentation ratio and viscosity. However, minimum optimizations were generated under different conditions. To optimize the parameters using the three output responses, a compromise among the conditions for different responses is desirable. The notion of a desirability function was employed, for which the total desirability was determined as a geometric mean of the individual desirability functions.^28,29 To determine the optimal conditions, the desirability function was fit using the least-squares model. Generally, a qualified SC product should include an aqueous separation ratio lower than 5% and centrifugal sedimentation ratio lower than 5%. The viscosity is relevant to fluidity and dispersibility of a preparation, and high viscosity often yields poor fluidity and dispersibility. Fortunately, the sample viscosity ranged from 160.34 mPa s to 345.78 mPa s. Because the viscosity was not of concern, it was considered a less important response during the optimization process. The optimized conditions were derived by minimizing the above three responses; the constraints are shown in Table S7 (ESI†). The level of variability that yielded the highest desirability (>0.90) was then used as the optimum level. Twenty-four solutions were generated when only the preparation formula was considered. However, we also expected to use as little dispersant as possible due to financial constraints. Therefore, the integrated optimum of variables were X₁ = 1.80, X₂ = −1.99, X₃ = 1.84 and X₄ = 0.66; the true mass fractions of each component were 2.90% Tersperse2700, 0.50% AE1601, 0.24% xanthan gum and 1.33% Veegum, respectively. The predicted values calculated using eqn (2)–(4) were 1.82% (R₁), 2.74% (R₂) and 254.11 mPa s (R₃), respectively. The SC sample prepared under optimal conditions was also produced and tested. The measured sample values for R₁, R₂ and R₃ were 1.69% ± 0.18%, 2.63% ± 0.27% and 257.74 ± 0.35 mPa s (mean ± standard error). The average relative errors of the predicted values above were 7.69%, 4.18% and −1.41%, respectively. As shown above, the desirability function introduced herein exhibited favorable effectiveness at multiple-response optimization. However, it should be noted that the fitness of the applied regression model decreased with the imported dependent variables; it was better to remove the unimportant indexes in the formulation before the multiple-response optimization.

Experimental

Materials

Thiacloprid (purity > 95%) was purchased from Shandong Sino-Agri United Biotechnology Co. Ltd. (Shandong, China) to prepare the SC. Agricultural emulsifier no. 1601 (AE1601) was purchased from the Jiangsu Hai'an Petrochemical Plant (Jiangsu, China), and Tersperse2700 (polycarboxylate, M_w = 7808), which is a type of high-efficiency dispersant, was provided by Huntsman (Salt Lake City, USA). Xanthan gum (purchased from Deosen Biochemical Ltd., Shandong, China) and magnesium aluminium silicate (Veegum, provided by Sinoma Mineral Materials Company, Jiangsu, China), known as anti-settling agents, were used to adjust the viscosity of the preparation.

Suspension concentrate preparation

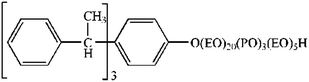
AE1601 is a segmented copolymer with the structure EO–PO–EO (ethylene oxide–propylene epoxide–ethylene oxide), which yields favorable wettability and thus plays a role as a wetting agent.³⁰ Tersperse2700 is a comb-polymer with high levels of carboxyl groups in its molecular structure, which produce effective charge repulsion.³¹ Furthermore, it can be adsorbed on the particle surface and exhibit favorable steric hindrance.³¹ Their chemical structures are shown as Scheme 1 and 2, respectively. It should be noted that both AE1601 and Tersperse2700 can provide wetting or dispersing functions; therefore, they were used as the investigated factors herein. Xanthan gum is a polysaccharide with a distinctive anti-settling specialty and is commonly used in SC due to its shear thinning property.³² Shear thinning indicates that the SC will be highly viscous upon standing but very thin after applying stress or strain, which is a significant advantage for liquid preparations. Previous articles demonstrate that physical stability can be significantly meliorated through combining magnesium aluminium silicate and xanthan gum mainly due to a synergistic effect;³³ thus, magnesium aluminium silicate was also used as an anti-settling agent. The typical procedure used herein is as follows. Wet grinding was performed to generate a thiacloprid 25% SC, and the optimal grinding conditions were determined. First, 52.63 g thiacloprid technical material, a certain weight of wetting-suspending agents and anti-settling agents, 4 g glycerol and 1 g defoamer were accurately weighed, and distilled water was used to make up to 200 g. Next, the mixture was added to a stainless steel cup with 200 ml zirconium oxide beads. Finally, the samples were ground at 1700 rpm for 1 h to generate a homogeneous thiacloprid 25% SC. Cooling water was used throughout the grinding process to maintain a relatively stable temperature around the container.

Scheme 1 Chemical structure of AE1601.

Scheme 2 Chemical structure of Tersperse2700 (R₁, R₂ and R₃ are simple hydrophobic groups).

Response surface methodology experiment

The RSM is a useful model for clarifying how multiple variables influence the responses in a complicated but effective manner based on the experimental design.^34–38 Among the second-order RSM designs, the Box-Behnken design and central composite design (CCD) are the most frequently used designs.^39–41

The CCD is a five-level experimental design, and the Box-Behnken design is a three-level design; thus, the accuracy of the CCD experiments may be better. An additional advantage of CCD is that it can be used to avoid continued experimentation at extreme conditions. Such conditions are often difficult to generate or control; thus, they may increase the potential for equipment damage.¹¹ The CCD experiments were designed by Design Expert 8.05 (Stat-Ease Inc., Minneapolis, USA) with four factors at five levels. Both the factors and levels were derived from the literature.⁴² The data analyses and model building were also performed using the same software. To prepare the thiacloprid SC, wetting-suspending agents and anti-settling agents were added as listed in Table 3.

Table 3 Factors and levels for the RSM experiment

Factor (mass fraction)	Level
	−2	−1	0	1	2
X1: Tersperse2700/%	1.00	1.50	2.00	2.50	3.00
X2: AE1601/%	0.50	1.00	1.50	2.00	2.50
X3: xanthan gum/%	0.16	0.18	0.20	0.22	0.24
X4: Veegum/%	0.00	0.50	1.00	1.50	2.00

---

Measuring quality control indexes

In principle, two types of accelerated experiments were performed to assess the physical stability of the SC. In the first accelerated experiment, we measured thermal physical stability. First, 16 g of the prepared sample was accurately weighed using an analytical balance (±0.0001 g, Sartorius, Goettingen, Germany); it was then sealed in a 20 ml tube with a stopper. Next, the tube was transferred to an oven for 14 d at a constant temperature (54 ± 2 °C). To enhance the experimental precision, the measurements were repeated in triplicate. Aqueous separation after hot storage was used to evaluate the advantages to thermal physical stability as shown in eqn (5).where m_up and m_to are the weight of separated aqueous phase after hot storage and the total weight of the sealed sample, respectively. The data demonstrate that more aqueous separation yields worsen physical stability. The second accelerated test included measuring the centrifugal stability. An 8 g sample was accurately weighed and sealed in a 10 ml centrifuge tube. The sample was then centrifuged at 3000 rpm for 30 min in a high-speed refrigerated centrifuge (Hitachi, Tokyo, Japan). After centrifugation, the centrifuge tube was inverted for 60 s to remove the upper suspension and the residual substance at the bottom was regarded as sediment. The centrifugal sedimentation ratio was defined as the ratio of the sediment weight to the total weight of the sample. The experiment was repeated for each preparation, and the data were presented as the mean ± SE (standard error). A lower centrifugal sedimentation ratio indicates better physical stability.

A laser particle size analyzer (Zhuhai OMEC instrument Co. Ltd., Guangdong, China) was used to evaluate the thiacloprid SC size distribution. It was measured four times, and the median diameter (D₅₀) was the selected parameter. Most pesticide SC products are composed of pseudoplastic fluid, wherein the apparent viscosity decreases with the shear rate, which is shear thinning.⁴³ A rheometer (Brookfield, Massachusetts, USA) in a thermostatic bath (25 °C) was used, and the samples were measured at a 10 s⁻¹ shear rate through reading viscosity values every 20 s based on a previously reported method.⁴⁴ The sample dispersibility and suspensibility measurements were performed using the methods recommended by the Collaborative International Pesticides Analytical Council (CIPAC), namely CIPAC MT160 and CIPAC MT184, respectively.

Conclusion

The main factors that influenced the aqueous separation ratio (R₁), centrifugal sedimentation ratio (R₂) and viscosity (R₃) were xanthan gum (X₃), Veegum (X₄) and AE1601 (X₂) followed by Tersperse2700 (X₁). In addition, several interactions were significant. The optimal conditions were mainly based on the minimum R₁, R₂, and R₃; and financial cost was determined. The integrated optimum conditions were X₃ = 1.84, X₄ = 0.66, X₂ = −1.99 and X₁ = 1.80, namely, the true mass fractions for each component were 0.24%, 1.33%, 0.50% and 2.90%, respectively. The optimum conditions yielded R₁, R₂, and R₃ values at 1.69% ± 0.18%, 2.63% ± 0.27% and 257.74 ± 0.35 mPa s (mean ± SE) with the average relative predicted value errors being 7.69%, 4.18% and −1.41%, respectively. The RSM is an effective approach for optimizing the suspension concentrate formulation; moreover, it can promote comprehensive advantages by properly adjusting the levels of several adjuvants based on practical requirements.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

The authors gratefully acknowledge Ms Wei Mu from Shandong Agricultural University for her helpful suggestions for this manuscript. This work was supported by a grant from the Special Fund for Agro-scientific Research in the Public Interest from the Ministry of Agriculture of China (201303027).

Notes and references

1. M. A. Faers and G. R. Kneebone, Pestic. Sci., 1999, 55, 312–325.
2. S. Haas, H.-W. Hässlin and C. Schlatter, Colloids Surf., A, 2001, 183–185, 785–793.
3. H. Li, F. Lu, H. Wang, L. Zhai and X. Li, Chin. J. Appl. Chem., 2012, 29, 327–331.
4. C. Díez, E. Barrado, P. Marinero and M. Sanz, J. Chromatogr. A, 2008, 1180, 10–23.
5. Z. Wang and H. Wang, Chin. J. Aeronaut., 2012, 25, 887–895.
6. J. Luo, G. Zhu, F. Zhang, Q. Li, T. Zhao and X. Zhu, RSC Adv., 2015, 5, 6071–6078.
7. E. Helm and B. Trolle, Wallerstein Lab. Commun., 1946, 9, 181–191.
8. C. Ma, F. Liu, W. Mu, Z.-R. Han and Z.-L. Chen, Chin. J. Pestic. Sci., 2006, 8, 379–382.
9. D.-X. Zhang, F. Liu, G.-S. Zhang, B. Chen and X.-N. Yang, Sci. Agric. Sin., 2011, 44, 2469–2475.
10. G. Taguchi and M. S. Phadke, in Quality Control, Robust Design, and the Taguchi Method, ed. K. Dehnad, Springer, US, 1989, pp. 77–96.
11. E. McCarthy, S. Flick and W. Mérida, J. Power Sources, 2013, 239, 399–408.
12. J.-P. Zhang, X.-L. Hou, T. Yu, Y. Li and H.-Y. Dong, J. Integr. Agric., 2012, 11, 151–158.
13. G. E. P. Box and K. B. Wilson, J. Roy. Stat. Soc. B, 1951, 13, 1–45.
14. W. Arbia, L. Adour, A. Amrane and H. Lounici, Food Hydrocolloids, 2013, 31, 392–403.
15. K.-N. Chen, M.-J. Chen and C.-W. Lin, J. Food Eng., 2006, 76, 313–320.
16. M. Aghbashlo, H. Mobli, S. Rafiee and A. Madadlou, Powder Technol., 2012, 225, 107–117.
17. J.-P. Wang, Y.-Z. Chen, Y. Wang, S.-J. Yuan and H.-Q. Yu, Water Res., 2011, 45, 5633–5640.
18. M. O. Hamzah, B. Golchin and C. T. Tye, Construct. Build. Mater., 2013, 47, 1328–1336.
19. L. Xin, X. Jinyu and L. Weimin, RSC Adv., 2015, 5, 1598–1604.
20. N. J. Bostanian, J. M. Hardman, H. A. Thistlewood and G. Racette, Pest Manage. Sci., 2010, 66, 1263–1267.
21. A. Elbert, M. Haas, B. Springer, W. Thielert and R. Nauen, Pest Manage. Sci., 2008, 64, 1099–1105.
22. S. Dong, K. Qiao, H. Wang, Y. Zhu, X. Xia and K. Wang, Pest Manage. Sci., 2014, 70, 1267–1273.
23. S. Dong, K. Qiao, Y. Zhu, H. Wang, X. Xia and K. Wang, Crop Prot., 2014, 58, 1–5.
24. T. Nakamura, H. Shimizu, M. Fujimoto, Y. Takahi and Y. Kondo, J. Pestic. Sci., 1981, 6, 293–300.
25. J. Liu, F. Chen, W. Tian, Y. Ma, J. Li and G. Zhao, J. Agric. Food Chem., 2014, 62, 7532–7540.
26. G. Peretto, W.-X. Du, R. J. Avena-Bustillos, J. D. J. Berrios, P. Sambo and T. H. McHugh, J. Agric. Food Chem., 2014, 62, 984–990.
27. M. Ghadiri, S. Fatemi, A. Vatanara, D. Doroud, A. R. Najafabadi, M. Darabi and A. A. Rahimi, Int. J. Pharm., 2012, 424, 128–137.
28. Z. He, P.-F. Zhu and S.-H. Park, Eur. J. Oper. Res., 2012, 221, 241–247.
29. H. Heidari and H. Razmi, Talanta, 2012, 99, 13–21.
30. X.-G. Zhang, J.-X. Liu, H.-Y. Wang, M.-Y. Wang and Z.-J. Fan, Acta Phys.-Chim. Sin., 2010, 26, 617–625.
31. C. Ma, Y. Xu, X.-Y. Guo, X.-R. Luo and X.-M. Wu, Chem. J. Chin. Univ., 2013, 34, 1441–1449.
32. D. Pooja, S. Panyaram, H. Kulhari, S. S. Rachamalla and R. Sistla, Carbohydr. Polym., 2014, 110, 1–9.
33. B. Li, K. Wang, D. Zhang, C. Zhang, L. Guan and F. Liu, Chin. J. Pestic. Sci., 2013, 15, 692–698.
34. V. B. Silva and A. Rouboa, Appl. Math. Comput., 2012, 218, 6733–6743.
35. F. Tabandeh, M. Khodabandeh, B. Yakhchali, H. Habib-Ghomi and P. Shariati, Chem. Eng. Sci., 2008, 63, 2477–2483.
36. M. Aghbashlo, H. Mobli, A. Madadlou and S. Rafiee, J. Microencapsulation, 2012, 29, 790–804.
37. S. Mayengbam, H. Yang, V. Barthet, M. Aliani and J. D. House, J. Agric. Food Chem., 2013, 62, 419–426.
38. B. S. Kaith, R. Sharma, S. Kalia and M. S. Bhatti, RSC Adv., 2014, 4, 40339–40344.
39. V. Hosseinpour, M. Kazemeini and A. Mohammadrezaee, Chem. Eng. Sci., 2011, 66, 4798–4806.
40. N. Şahín, C. C. Akoh and A. S. Karaalí, J. Agric. Food Chem., 2006, 54, 3717–3722.
41. E. Pourbasheer, S. Sadafi, M. R. Ganjali and M. Abbasghorbani, RSC Adv., 2014, 4, 62190–62196.
42. B. Li, W. Wang, D. Zhang, K. Wang, L. Guan and F. Liu, Sci. Agric. Sin., 2015, 48, 280–292.
43. J. Shen, Q.-L. Huang, J.-B. Xia, D. Chen, D.-M. She, F.-M. Li and W. Hu, Chin. J. Pestic. Sci., 2008, 10, 354–360.
44. L.-F. Li, L. Wang, J.-W. Wang and D.-Q. Wang, Acta Chim. Sin., 2011, 69, 1760–1764.

---

Footnote

† Electronic supplementary information (ESI) available: The design matrix for the proposed experiments and their corresponding output parameters are shown in Table S1. The regression equation coefficients and ANOVA for the aqueous separation ratio (Table S2), centrifugal sedimentation ratio (Table S4) and viscosity (Table S6) are listed as supplementary information. The fitness of centrifugal sedimentation ratio results to different models is listed as Table S3, and that for viscosity is displayed in Table S5. Moreover, the constraints for the multiple-response optimization are shown in Table S7. Fig. S1 and S2 which illustrated the measured values vs. predicted values for modelled centrifugal sedimentation ratio and viscosity are also listed. See DOI: 10.1039/c5ra00292c

---