TD-DFT calculations of UV absorption bands and their intensities in the spectra of some tetrahydroquinolines†
María V. Cookea,
Ivana Malvacioa,
Walter J. Peláez*a,
Ana J. Pepinoa,
María R. Mazzierib and
Gustavo A. Argüelloa
aINFIQC-CONICET-Dpto. de Fisicoquímica, Facultad de Ciencias Químicas, Universidad Nacional de Córdoba, Ciudad Universitaria, Córdoba, X5000HUA, Argentina. E-mail: waldemar31@fcq.unc.edu.ar
bDepartamento de Farmacia Facultad de Ciencias Químicas, Universidad Nacional de Córdoba, Ciudad Universitaria, Córdoba, X5000HUA, Argentina
First published on 4th March 2015
Abstract
A detailed analysis of the MOs involved in electronic transitions in UV spectra as well as a conformational study of 1-benzenesulfonyl-1,2,3,4-tetrahydroquinoline (BSTHQs) derivatives have been carried out using the TD-DFT (B3LYP/6-31+G(d,p)) method. Based on experimental solvent effects and theoretical investigations the long-wavelength bands have been assigned to π → π* transitions caused by HOMO–LUMO intramolecular charge transfer from the tetrahydroquinoline fragment (THQ) to the benzenesulfonyl moiety (BS). Nevertheless, for the NO2 derivative the HOMO–LUMO transition was found to be forbidden. In this case the long-wavelength band has been associated to an n → π* transition. Good correlation of theoretical and experimental data for the energy transitions and the molar extinction coefficients of the compounds studied has been obtained and is presented for the first time.
Introduction
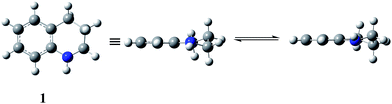
1,2,3,4-tetrahydroquinoline (THQ, 1) and benzenesulfonyl (BS) derivatives are structures with well known biological activities. The THQ moiety is present in compounds with diverse characteristics such as antimalarial1 and anticancer activity,2 nonsteroidal glucocorticoid receptor ligands,3 agonists of β3 adrenergic receptors,4 and histamine H3 receptor antagonists,5 among others. On the other hand, the BS group is a substituent frequently present in biologically active molecules,6–8 where the presence of the BS group leads to analogues with similar or better biological activities than their precursors.9 In particular, we demonstrated that 1-benzenesulfonyl-1,2,3,4-tetrahydroquinolines (BSTHQs 2–5, Fig. 1) which are a combination of these active moieties, possess interesting properties such as antiparasitic activity,10 while others have shown different behavior as HIV-transcriptase inhibitors,11 low potency calcium channel antagonists12 and gonadotropin releasing hormone antagonists,13 respectively. | ||
| Fig. 1 1,2,3,4-tetrahydroquinoline (THQ, 1) and 1-benzenesulfonyl-1,2,3,4-tetrahydroquinolines derivatives (BSTHQs 2–5) studied in the present work. | ||
As part of our ongoing project on N-benzenesulfonyl derivatives as bioactive heterocyclic compounds, our research has been focused on exploring the consequences of a BS–N linkage on the stereoelectronic properties of some 1-benzenesulfonyl-1,2,3,4-tetrahydroquinolines (2–5, Fig. 1). Experimental (UV-Vis) and theoretical calculations TD-DFT (B3LYP/6-31+G(d,p)14,15 and CAM-B3LYP/6-31+G(d,p)16,17) have been carried out aiming to determine the nature of electronic transitions and their dependences. The selection of the species under study was mainly guided by electronic considerations going from electron-donating, such as –NH2, to electron-withdrawing, such as –NO2 (as defined by the Hammet constant, σ18).
Studying the electronic structure by UV spectral and quantum chemical methods is important, not only for interpretation of the spectra, but also to estimate the direction of the electronic density redistribution of the compounds, which is a determining factor of their reactivity and biological activity.
Results and discussion
Conformational analysis
In a previous work,10 we performed some conformational analysis on THQ 1 and BSTHQs 2–5 with the semiempirical (AM1) and DFT (B3LYP/6–31G(d)) methods, as implemented in Gaussian 03. New calculations here confirm the proposed conformational structures established by Charifson et al.8 where the THQ 1 was found to present two equivalent half-chair conformations, while the half-boat conformations were not stable (Fig. 2).The new calculations presented here (BSTHQs at DFT-B3LYP/6-31+G(d,p) method) deal particularly with the contribution of each conformer to the total UV spectrum in the different solvents. New careful geometry optimizations were performed to establish the position of the BS group and the relative populations of the different conformers in solution (acetonitrile ACN, ethanol EtOH and dichloromethane DCM) to determine which one contributes more to the electronic spectrum.
For BSTHQs, scans of the two relevant dihedral angles were used to inspect the positioning of sulfonyl (α dihedral) and phenyl (β dihedral) substituents. Two minimum-energy conformations for each BSTHQ derivative were found and characterized as stationary points by vibrational frequency calculations. For all BSTHQ 2–5, the BS group was shown to be in pseudo-axial position, while the phenyl substituent adopts two different (-in and -out) configurations (Scheme 1) with relative populations given by the Boltzmann distribution which are presented in Table S1 (ESI†).
The scheme also shows both the HOMO and the LUMO orbitals in an attempt to rationalize (as it will be discussed later), from a geometrical point of view, the lowest allowed transition in the UV spectrum.
For BSTHQ 2, the -in configuration amounted to 68.6%, while for the others (3–5) were higher than 85% (91.3, 90.9 and 88.2% respectively). Calculations of specific NBO (Natural Bond Order) donor–acceptor interactions were performed in order to explain these differences. The explanation lies mainly on the effective energy interaction between the π*C10–C12 antibonding orbital of the phenyl ring and the two π* orbitals that involve C11–C13 and C14–C15, which are present only in the conformers with -in conformation of compounds 3–5.
Analysis of MO formation
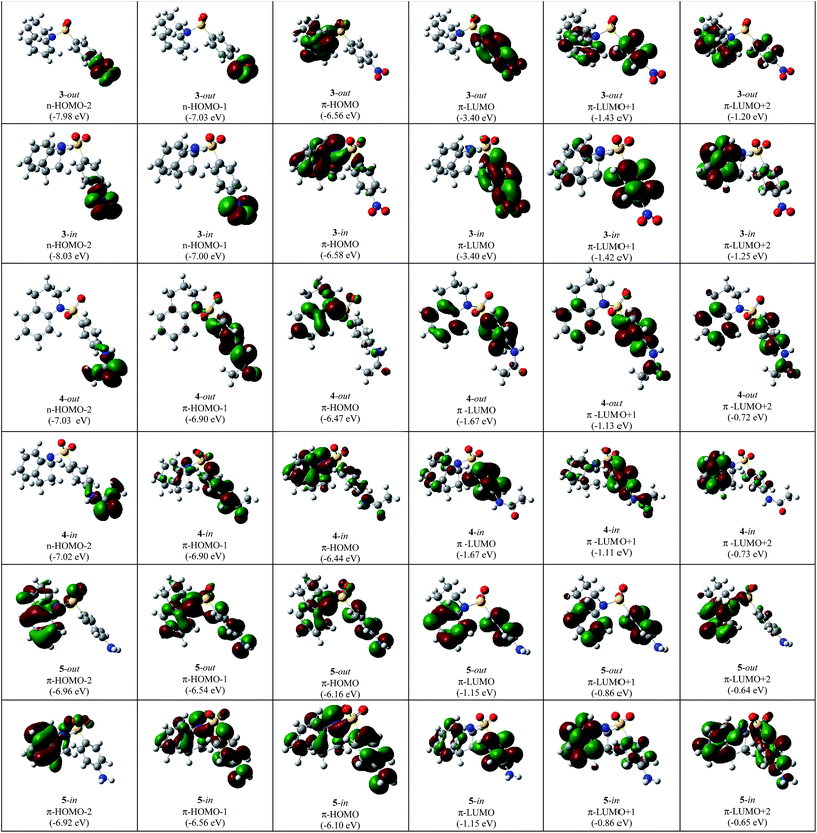
In Fig. 3 and 4 the type, energy and shapes of MOs of THQ 1 and BSTHQ 2–5 in ACN solvent are presented. The MOs compositions were calculated using the GaussSum software.19 | ||
| Fig. 3 The type, energy (in parenthesis) and shapes of MOs of THQ 1 BSTHQ 2 in ACN solvent by DFT (B3LYP/6-31G+(d,p)) method. | ||
 | ||
| Fig. 4 The type, energy (in parenthesis) and shapes of MOs of BSTHQ 3–5 in ACN solvent by DFT (B3LYP/6-31G+(d,p)) method. | ||
In compounds 2–5, the occupied orbitals are mainly localized on the tetrahydroquinoline fragment while the unoccupied orbitals have their major contribution from the phenyl ring. These results suggest that all the transitions involve charge transfer from the thetrahydroquinoline to the phenyl moiety.
The highest occupied MO (HOMO) of THQ nucleus 1 has mainly n-symmetry and is localized on the nitrogen atom (61%). The other orbitals shown (HOMO − 2, HOMO − 1, LUMO, LUMO + 1 and LUMO + 2) have π-symmetry localized on the benzene ring (>60%) and the nitrogen atom (∼30%), Fig. 3.
For compounds 2–5, the HOMO has π-symmetry with the main contribution from the tetrahydroquinoline fragment and some from the phenyl ring (2: 93/7%, 3: 93/6%, 4: 59/23% and 5: 88/3% Fig. 3 and 4). The second-highest occupied MO (HOMO − 1) is also π-symmetry in all cases except for compound 3 in which it has n-symmetry localized on the substituent –NO2 of BS moiety (>60%). Nevertheless, the symmetry of HOMO − 2 MOs for all BSTHQ depend strongly on the substituent in the BS moiety. In the cases where the substituent possess more than one heteroatom with free electron pairs, the MOs have an n-type symmetry localized on the heteroatoms, particularly on the oxygen (3: –NO2 fragment, 60%; 4: –NH–COCH3, 75%). Meanwhile, for BSTHQ 2 and 5, the symmetry of the HOMO − 2 MOs is π-type and have a significant contribution from the quinoline fragment (97%).
On the other hand, the lowest unoccupied MO (LUMO), LUMO + 1 and LUMO + 2 have π-symmetry for all BSTHQ (Fig. 3 and 4). LUMO and LUMO + 1 are mostly localized on the BS group with the exception of compound 5 in the -in conformation where LUMO + 1 is localized on the tetrahydroquinoline moiety. LUMO + 2 MOs are also localized on the tetrahydroquinoline moiety, with exception of conformers 4-out and 5-in where these are localized ∼50 percent on each fragment.
UV measurements
The UV spectra were recorded in ACN, EtOH and DCM in order to obtain information about the nature of the transitions involved in the main bands, Fig. 5. | ||
| Fig. 5 (a–e) UV spectra of compounds 1–5 in EtOH, ACN and DCM. (f) UV spectra of compounds 1–5 in ACN. | ||
As it can be seen all compounds present three distinctive absorption regions that will be roughly named short (190–220 nm), medium (220–280 nm) and long (280–360 nm) wavelength regions.
In the short wavelength region, all compounds present the most intense band. At longer wavelengths, the THQ nucleus (1) manifests two broad bands in the medium and long regions. The N-substitution by the BS group yields compound 2, which has a less structured spectrum with two weak broad bands in the medium region between 220–250 nm and 260–280 nm. Compound 3 presents a spectrum similar to 2, while 4 and 5 exhibit an intense band with its maximum at ∼270 nm.
The λmax at ∼270 nm of compounds 4 and 5 moves to longer wavelenghts (bathochromic shift) in solvents of increasing polarity which suggests that it could be associated to a π → π* transition, Table 1. Otherwise, the corresponding band in compound 3 (∼293 nm) shows the opposite behavior which could be associated to a n → π* transition. Table 1 lists experimental λmax (nm) and ε (M−1 cm−1), where the blue arrows show the shifting in wavelengths while the red ones mark the changes in intensity with the change in polarity of the solvent.
In addition, no clear solvent effects were observed for the other absorption maxima of 1 and 2, which would suggest that these are not pure transitions, but combinations.
UV calculations
TD-DFT calculations were used to simulate the UV spectra and to determine the MOs involved in each transition. These calculations were performed in ACN, EtOH and DCM with B3LYP and CAM-B3LYP functional methods since it is known that having transitions with charge transfer character, the latter method should perform better.After analyzing the lowest optically active excitation energy for the most abundant conformer of compounds 2–5, there was not a clear trend in the shifting of the bands with the solvent, as can be seen in Table S3 of the ESI.† The CAM-B3LYP functional method was appropriate to describe the positioning of the absorption bands for compound 3 (providing a wavelength value closer to the experimental one) though did not show any trend with the change of polarity in the solvent.
The experimental maxima and calculated UV spectral data of 1–5 in ACN solvent are given in Table 2. The experimental absorption maxima were determined with the aid of the second derivative spectra. From the analysis of the results, we conclude that the bands in the short wavelength region are a combination of different transitions, as it was expected from solvent effects.
| Entry | Compound (% in/out) | Experimentala | Calculated (TD-DFT)b | Transitionc | Assignament | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| in | out | ||||||||||
| λexpmax (nm) | εexp | λcalcmax (nm) | f | εcal | λcalcmax (nm) | f | εcal | ||||
| a Peak maxima were determined using a second derivative based method.b TD-B3LYP 6-31+G(d,p).c H-highest occupied MO (HOMO), L-lowest unoccupied MO (LUMO). | |||||||||||
| 1 | 1 (50/50) | 208 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
200 | 0.177 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
200 | 0.177 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
H − 1 → L + 2 | π → π* |
| 2 | 204 | 0.237 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
204 | 0.237 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
H − 1 → L | π → π* | |||
| 3 | 205 | 0.195 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 137 |
205 | 0.195 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 137 |
H − 1 → L + 1 | π → π* | |||
| 4 | 253 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
247 | 0.125 | 8401 | 247 | 0.125 | 8401 | H → L + 2 | π → π* | |
| 5 | 305 | 3650 | 287 | 0.064 | 4339 | 287 | 0.064 | 4339 | H → L | π → π* | |
| 6 | 2 (54/46) | 204 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
201 | 0.068 | 4602 | 199 | 0.180 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 119 |
H − 2 → L + 2/H − 2 → L + 1 | π → π* |
| 7 | 205 | 0.050 | 3360 | 208 | 0.106 | 7119 | H → L + 5/H − 1 → L + 3 | π → π* | |||
| 8 | 219 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
211 | 0.162 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
222 | 0.097 | 6572 | H − 1 → L + 2/H − 2 → L | π → π* | |
| 9 | 219 | 0.076 | 5115 | 225 | 0.107 | 7240 | H − 3 → L/H − 1 → L + 1 | π → π* | |||
| 10 | 237 | 7190 | 236 | 0.046 | 3070 | 237 | 0.036 | 2463 | H − 2 → L | π → π* | |
| 11 | 238 | 0.047 | 3198 | 241 | 0.156 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533 533 |
H → L + 3/H → L + 2 | π → π* | |||
| 12 | 258 | 5790 | 245 | 0.049 | 3320 | 257 | 0.029 | 1937 | H → L + 2/H → L + 1 | π → π* | |
| 13 | 271 | 4350 | 292 | 0.176 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 869 869 |
288 | 0.023 | 1572 | H → L | π → π* | |
| 14 | 3 (91/9) | 202 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
202 | 0.157 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 567 |
204 | 0.069 | 4656 | H − 2 → L + 1 | π → π* |
| 15 | 208 | 0.176 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862 862 |
207 | 0.253 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
H − 1 → L + 4 | π → π* | |||
| 16 | 210 | 0.076 | 5101 | 211 | 0.073 | 4953 | H → L + 5 | π → π* | |||
| 17 | 238 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 240 |
235 | 0.052 | 3482 | 238 | 0.161 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
H → L + 4 | π → π* | |
| 18 | 253 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
261 | 0.098 | 6586 | 271 | 0.181 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 186 |
H → L + 2/H − 1 → L + 2 | π → π*/π → π* | |
| 19 | 257 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 910 |
265 | 0.126 | 8482 | — | — | — | H → L + 2/H − 4 → L | π → π*/π → π* | |
| 20 | 294 | 4590 | 297 | 0.230 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
300 | 0.190 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
H − 2 → L | π → π* | |
| 21 | 302 | 4540 | |||||||||
| 22 | 305 | 4440 | |||||||||
| 23 | 310 | 4300 | |||||||||
| 24 | — | — | 454 | 0.064 | 4318 | 459 | 0.025 | 1694 | H → L | π → π* (optically inactive) | |
| 25 | 4 (90/10) | 205 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
205 | 0.277 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 952 |
205 | 0.146 | 7897 | H − 2 → L + 3 | π → π* |
| 26 | 215 | 0.111 | 5970 | 214 | 0.152 | 8210 | H − 4 → L | π → π* | |||
| 27 | 240 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
240 | 0.085 | 4594 | 242 | 0.115 | 6202 | H → L + 2 | π → π* | |
| 28 | 256 | 0.371 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
257 | 0.170 | 9193 | H − 2 → L | π → π* | |||
| 29 | 265 | 0.062 | 3368 | 263 | 0.463 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 966 |
H − 1 → L | π → π* | |||
| 30 | 269 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
297 | 0.297 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 037 |
297 | 0.083 | 4459 | H → L | π → π* | |
| 31 | 5 (87/13) | 199 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
198 | 0.131 | 8859 | 200 | 0.121 | 8164 | H − 4 → L/H − 3 → L + 1 | π → π* |
| 32 | 205 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
208 | 0.213 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 365 |
208 | 0.099 | 6694 | H − 2 → L + 3 | π → π* | |
| 33 | 209 | 0.109 | 7355 | 212 | 0.211 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 217 |
H → L + 6/H − 3 → L | π → π* | |||
| 34 | 212 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
214 | 0.114 | 7672 | 213 | 0.062 | 4150 | H − 3 + L/H − 2 → L + 2 | π → π* | |
| 35 | 244 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
245 | 0.088 | 5918 | 232 | 0.067 | 4501 | H − 1 → L + 1/H − 1 → L + 2 | π→π* | |
| 36 | 247 | 0.084 | 5702 | 259 | 0.304 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 539 539 |
H − 1 → L + 1/H − 1 → L | π → π* | |||
| 37 | 271 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
283 | 0.316 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342 |
278 | 0.127 | 8590 | H → L | π → π* | |
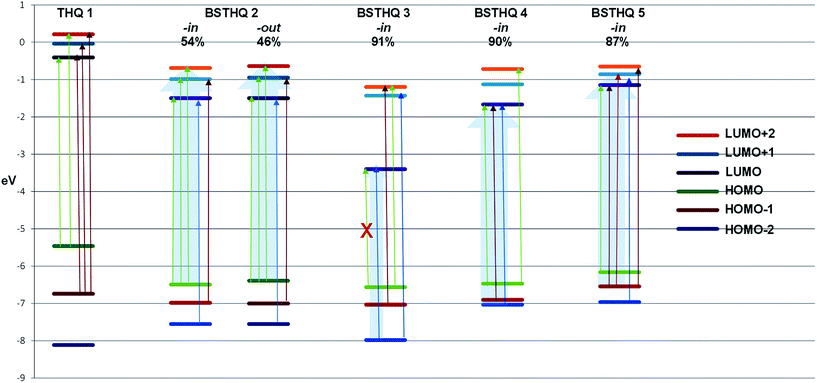
On the other hand, the maximum at the longest wavelength region in compounds 4 and 5 corresponds to the HOMO → LUMO transition which has a π → π* nature caused by intramolecular charge transfer from the quinoline to the BS group (entries 30 and 37, Table 2). This is also in agreement with the bathochromic shift observed in polar solvents.
The most remarkable result lies on compound 3. The calculated TD-B3LYP π → π* HOMO → LUMO transition occurs at longer wavelengths (∼454 nm) (entry 24, Table 2). The TD-CAM-B3LYP functional method16,17 gave a more realistic value with the transition appearing at ∼297 nm. This π → π* transition does not seem to be in agreement with the results obtained from the solvent effects, where it was said to be a n → π* transition. Comparing the oscillator strengths (f) of the HOMO–LUMO transition between 3 (entry 24, Table 2) and 2, 4 and 5 (-in conformation, entries 13, 30 and 37, Table 2), the former is approximately five times smaller. Therefore, the n → π* nature of the long wavelength transition does not arise from the HOMO → LUMO transition but it comes from the HOMO − 2 → LUMO excitation (f = 0.230, entry 21, Table 2), in agreement with the solvent effects.
Further analysis of the MOs for compounds 3 to 5 have shed some light as to why HOMO → LUMO appears to be optically inactive (f = 0.064) for 3. HOMO of 4 and 5, allows us to see that there is a contribution to this orbital from the phenyl ring of the BS moiety that is absent for 3 (-in conformation, Fig. 4). In the same way, for the LUMO there is a contribution from the aromatic ring of the quinoline moiety for compound 4 and 5 that does not occur for the LUMO of 3. These differences indicate that the intramolecular charge transfer for 4 and 5 is not pure for the HOMO–LUMO transition compared to what happens in 3. Nevertheless, there is a substantial contribution from the substituent NO2 (59%) to the LUMO of 3, while no contribution to the LUMO of 4 and 5 from the corresponding substituent was observed. This is the reason of the underestimation of the energy in this transition, as it is known for TD-B3LYP calculations. In Fig. 6, we present the relative energy of MOs highlighting the transitions that contribute to the experimental bands that appear at the long wavelength region of the UV spectra. It is noteworthy that only for 3, the contribution comes from one transition while for 2, 4 and 5 there is a general pattern of three transitions very close in energy.
Conclusions
A conformational analysis of THQ and its BS derivatives was performed and allowed us to assess that the main contribution to the total UV spectrum comes from the -in conformer. The UV spectra of compounds 1–5 in acetonitrile, ethanol and dichloromethane were measured. On the basis of experimental and theoretical investigations by the DFT methods, the long-wavelength bands of BSTHQ derivatives have been assigned to π → π* (HOMO → LUMO) transitions were an intramolecular charge transfer from the THQ fragment to the BS group takes place. Nevertheless, for BSTHQ 3, the expected HOMO–LUMO transition appears to be optically inactive. In this case, the long-wavelength transition observed was assigned to HOMO − 2 → LUMO which suggests an n → π* character.It was also shown that the calculated electronic transitions as well as the molar absorption coefficients which resulted from applying TD-DFT (B3LYP/6-31+G(d,p)) calculations are in agreement with experimental data. Such correlations were carried out for the first time.
Experimental
Experimental methods
Compounds 2–5 were synthetized as described elsewhere.10 All of them were characterized by standard spectroscopic techniques as 1H NMR, 13C NMR, HMBC, HSQC, UV and IR and mass spectrometry. All the physicochemical data were identical to those described before10 and all of them are presented in the ESI.†The UV spectra were measured in ethanol, dichloromethane and acetonitrile (all HPLC grade) solutions using 1 cm quartz cells on a UV-71601 Shimadzu spectrophotometer. The concentrations were in the range 1–5 × 10−5 M.
Computational methods
Conformational and MO calculations have been performed using the Gaussian 09 program.20 The ground state geometries were fully optimized using the hybrid B3LYP and CAM-B3LYP functional methods, in combination with the 6-31+G(d,p) basis set. The relative population of the conformers was calculated using the Boltzmann population distribution equation.21 For each optimized structure, a frequency analysis at the same level of theory was used to verify that it corresponds to a minimum in the potential energy surface. For all the minima, the number of imaginary frequencies was zero. The excited state properties were calculated with the time-dependent density functional (TD-DFT) formalism. Contrary to the semi-empirical approaches by which other systems have been studied before,22 TD-DFT23–25 is based on first principles and thus has enabled the study of excitation energies, oscillator strengths and polarizabilities of larger systems. TD-DFT in combination with the B3LYP hybrid functional and the 6-31+G(d,p) basis set has previously been shown to provide accurate energies for excited states within 0.2 eV (5 kcal mol−1).26 The polarizable conductor calculation model (C-PCM) of solvation was used in all calculations.27,28Theoretical coefficients (εcalc) have been calculated by the formula (1):29
| εcal = f × 2.699 × 104/b, | (1) |
Acknowledgements
Thanks are due to CONICET, SECYT and FONCYT for financial support. M. V. C., I. M. and A. J. P. acknowledge Doctoral fellowships from CONICET.Notes and references
- M. K. Gupta and Y. S. Prabhakar, Eur. J. Med. Chem., 2008, 43(12), 2751–2767 CrossRef CAS PubMed.
- J. P. Liou, Z. Y. Wu, C. C. Kuo, C. Y. Chang, P. Y. Lu, C. M. Chen, H. P. Hsieh and J. Y. Chang, J. Med. Chem., 2008, 51(14), 4351–4355 CrossRef CAS PubMed.
- S. L. Roach, R. I. Higuchi, M. E. Adams, Y. Liu, D. S. Karanewsky, K. B. Marschke, D. E. Mais, J. N. Miner and L. Zhi, Bioorg. Med. Chem. Lett., 2008, 18(12), 3504–3508 CrossRef CAS PubMed.
- N. Shakya, K. K. Roy and A. K. Saxena, Bioorg. Med. Chem., 2009, 17(2), 830–847 CrossRef CAS PubMed.
- C. D. Jesudason, L. S. Beavers, J. W. Cramer, J. Dill, D. R. Finley, C. W. Lindsley, F. C. Stevens, R. A. Gadski, S. W. Oldham, R. T. Pickard, C. S. Siedem, D. K. Sindelar, A. Singh, B. M. Watson and P. A. Hipskind, Bioorg. Med. Chem. Lett., 2006, 16(13), 3415–3418 CrossRef CAS PubMed.
- M. C. Davis, S. G. Franzblau and A. R. Martin, Bioorg. Med. Chem. Lett., 1998, 8(7), 843–846 CrossRef CAS.
- L. Garuti, M. Roberti and C. Cermelli, Bioorg. Med. Chem. Lett., 1999, 9(17), 2525–2530 CrossRef CAS.
- P. S. Charifson, J. P. Bowen, S. D. Wyrick, A. J. Hoffman, M. Cory, A. T. McPhail and R. B. Mailman, J. Med. Chem., 1989, 32(9), 2050–2058 CrossRef CAS.
- S. Lee, S. Oh, G. M. Park, T. S. Kim, J. S. Ryu and H. K. Choi, Korean J. Parasitol., 2005, 43(3), 123–126 CrossRef.
- R. J. Pagliero, A. B. Pierini, R. Brun and M. R. Mazzieri, Lett. Drug Des. Discovery, 2010, 7(6), 461–470 CrossRef CAS.
- M. Zanger, Diarylsulfone non-nucleosidereverse transcriptase inhibitors of human imunodeficiency virus, US6063790, 2000.
- E. Carosati, G. Cruciani, A. Chiarini, R. Budriesi, P. Ioan, R. Spisani, D. Spinelli, B. Cosimelli, F. Fusi, M. Frosini, R. Matucci, F. Gasparrini, A. Ciogli, P. J. Stephens and F. J. Devlin, J. Med. Chem., 2006, 49(17), 5206–5216 CrossRef CAS PubMed.
- K. Hamamura, T. Oda, T. Kaku and T. Suzaki, Preparation of fused pyrimidine derivative as GnRH antagonists, WO 2006083005 A1 20060810, 2006.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- X. Liu, D. Yamg, H. Ju, F. Teng, Y. Hou and Z. Lou, Chem. Phys. Lett., 2011, 503, 75–79 CrossRef CAS PubMed.
- Exploring QSAR: Fundamentals and Application in Chemistry and Biology, C. Hansch and A. Leo, ACS Publications, 1995 Search PubMed.
- N. M. O' Boyle, A. L. Tenderholt and K. M. Longer, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Ioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, 7th edn, 2002 Search PubMed.
- A. R. Tameev, Z. He, G. H. W. Milburn, A. A. Kozlov, V. Vannikov, A. Puchala and D. Rasala, Appl. Phys. Lett., 2002, 81(6), 969–971 CrossRef CAS PubMed.
- G. Ricciardi, A. Rosa, S. J. A. Van Gisbergen and E. J. Baerends, J. Phys. Chem., 2000, 104(3), 635–643 CrossRef CAS.
- S. J. A. Van Gisbergen, J. A. Groeneveld, A. Rosa, J. G. Snijders and E. J. Baerends, J. Phys. Chem. A, 1999, 103(34), 6835–6844 CrossRef CAS.
- A. Rosa, E. J. Baerends, S. J. A. Van Gisbergen, E. Van Lenthe, J. A. Groeneveld and J. G. Snijders, J. Am. Chem. Soc., 1999, 121(44), 10356–10365 CrossRef CAS.
- J. Llano and L. A. Eriksson, Phys. Chem. Chem. Phys., 2004, 6, 4707–4713 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102(11), 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24(6), 669–681 CrossRef CAS PubMed.
- H. Baumann, R. E. Martin and F. Diederich, J. Comput. Chem., 1999, 20, 396–411 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization of compounds 1–5 and Cartesian Coordinates (Å) obtained from the DFT (B3LYP/6-31+G(d,p)) computational calculations are provided. See DOI: 10.1039/c5ra00249d |
| This journal is © The Royal Society of Chemistry 2015 |