Largely improved electromechanical properties of thermoplastic polyurethane dielectric elastomer by carbon nanospheres
Yang Yaoa,
Nanying Ningab,
Liqun Zhangab,
Toshio Nishic and
Ming Tian*ab
aCollege of Materials Science and Engineering, State Key Lab of Organic–Inorganic Composites, Beijing University of Chemical Technology, 15th BeiSanHuan East Road, ChaoYang District, Beijing 100029, China. E-mail: tianm@mail.buct.edu.cn
bKey Laboratory of Carbon Fiber and Functional Polymers, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
cDepartment of Applied Physics, The University of Tokyo, Hongo, Bunkyo-ku, Tokyo, Japan
First published on 24th February 2015
Abstract
Carbon nanospheres (CNS) were used as a new conductive filler to improve the electromechanical properties of a thermoplastic polyurethane (TPU) dielectric elastomer (DE). The results showed that CNS with many hydroxyl groups can form hydrogen bonds with TPU molecules, leading to a good dispersion of CNS in the TPU matrix and an improved tensile strength of CNS/TPU composites. More interestingly, CNS disrupted the crystallization of TPU, resulting in the decrease in elastic modulus and hysteresis loss of the composites. The dielectric constant at 1000 Hz increased from 7.1 for pure TPU to 137.3 for the composite with 5 wt% of CNS. The great increase in dielectric constant and the decrease in elastic modulus result in the largely improved actuation strain at low electric field of CNS/TPU composites. In addition, all the as-prepared CNS/TPU composites have a low dielectric loss (<1) at 1000 Hz. Our study provides a simple and effective way to obtain CNS/TPU DE with good mechanical strength and largely improved actuation performance at low electric field.
1. Introduction
Dielectric elastomer actuators (DEAs), consisting of an elastomer film sandwiched between two compliant electrodes, can act as electromechanical transducers that transform electrical energy to mechanical energy.1 Compared with conventional smart materials such as shape memory alloys and electroactive ceramics, DEAs have attracted much attention in the last two decades because they have many advantages such as low elastic modulus, large strain, fast response, light weight, reliability, high energy density, and high electromechanical coupling efficiency.2–4 DEAs find many applications in industry such as micro air vehicles, flat-panel speakers, inchworm robots,5 adaptive optical devices,6 aerodynamic and refreshable Braille displays.7 A key limitation for the practical application of DEAs is the requirement of high electric field (>100 V μm−1),8–10 which could be harmful to humans and damage equipment, particularly in biological and medical fields.11,12 Thus, large actuation strain at low electric field is the biggest challenge for DEAs.13The actuation in DEAs materials is due to the coupling of electrostatic stress with elastic stress.14,15 The electrostatic stress P (also called Maxwell's pressure) can be described by the equation,
| P = ε0εrE2 | (1) |
Based on linear-elasticity and free boundary approximations, the actuation strain SZ in thickness direction is given by
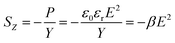 | (2) |
| SP = 1/(1 + Sz) − 1 | (3) |
According to eqn (2), β is defined as the ratio of the dielectric constant (εr) to the elastic modulus (Y) (β = εr/Y). To obtain a DE with high actuation strain at a low electric field, a high β is required. Accordingly, a substantial increase in εr and a substantial decrease in Y is a reasonable solution.7
One common approach to improve εr is to add ceramics with high εr into the elastomer matrix.2,19,20 Generally, the εr of the composites can be obviously improved by adding up to 50 vol% of the ceramics. A particular disadvantage is that the mechanical and processing properties are greatly deteriorated because of the high content of these fillers. Another widely used approach to improve εr of elastomer is to add conductive filler such as carbon nanotubes21 and graphene22 into the elastomer matrix. The εr of the elastomer can be greatly improved by adding a small content of these conductive fillers. However, these fibrous or sheet conductive fillers can significantly increase the elastic modulus of elastomer matrix.11 Carbon black is also a good candidate of dielectric filler because of its wide range of electrical properties and its large surface area. The disadvantage of carbon black is that it is easy to aggregate within polymer matrix.23 Some semiconducting polymers such as poly (hexylthiophene),9 polyaniline (PANI),24 and copper phthalocyanine oligomers (PolyCuPC)25 with high εr were also used to improve the actuated performance of elastomers. These semiconducting polymers were usually prepared by using very complicated chemical synthesis process.
Carbon nanosphere (CNS) is formed from the pairing of pentagonal and heptagonal carbon rings. In spherical nanostructure, the graphite sheets of CNS are not closed shells but rather waving flakes that follow the curvature of the sphere, creating many open edges at the surface. The unclosed graphite sheets provide reactive “dangling bonds”, facilitating the surface reactions of CNS with elastomer matrix.26 The properties of CNS are similar to graphite or fullerenes, which includes large packing density, high temperature stability, and excellent electrical conductivity.27,28 Thus, CNS can be used as good dielectric filler to largely improve the dielectric constant of elastomers. Meanwhile, comparing with graphene and CNTs, CNS, as a spherical particle, has less effect on increasing the elastic modulus of elastomer composites. In addition, there exist many hydroxyl groups on the surface of CNS,29 which may have a strong interaction with TPU molecules.
Silicones, acrylics, and polyurethanes are the three most promising groups of DE.7 Among these materials, thermoplastic polyurethanes (TPU) have good recyclability, good mechanical properties, large force output, and high εr, thus have received much attention in recent years. In addition, TPU is an ideal matrix for nanocomposites. For example, TPU/carbon black23 and TPU/silver composites30,31 have been widely studied. However, there exist a large number of hydrogen bonds between TPU molecules, which largely limit the polarizability of TPU chains. Thus, the εr of TPU is still needed to be improved.7,32 Meanwhile, TPU exhibits higher elastic modulus than that of silicon and acrylics, which is partly due to the crystallization in its structure.33,34 In this study, CNS was used as dielectric filler to improve the electromechanical properties of TPU for the following reasons. First, CNS with reactive “dangling bonds” and with many hydroxyl groups facilitate the formation of good interfacial interaction of CNS/TPU composites. Thus, a good dispersion of CNS in TPU matrix could be obtained. Meanwhile, the crystalline in TPU could be disrupted by adding CNS because of the strong interaction between CNS and TPU. Second, CNS with good electric conductivity could largely improve the dielectric constant of TPU. Third, CNS with spherical shape could not significantly increase the elastic modulus of CNS/TPU composite. We aim to improve the actuation performance at low electric field of TPU dielectric elastomer for its application in biological and medical areas and to study the effect of CNS on the mechanical and electromechanical properties of CNS/TPU composites.
2. Material and methods
2.1 Materials
Multi-hydroxyl-grouped carbon nanosphere (CNS) with an average diameter of 100 nm was fabricated by catalytic pyrolysis of heavy oil (C: 88.79%, H: 11.01%, N: 0.20%, China National Offshore Oil Corporation, China) at 1150 °C.35 It was kindly provided by Dr Huaihe Song, from State Key Laboratory of Chemical Resource Engineering in Beijing University of Chemical Technology. TPU (45A) was purchased from BASF Polyurethane Specialties (China) Co., Ltd. Dimethyl formamide (DMF) and tetrahydrofuran (THF) were supplied by Beijing Modern Eastern Fine Chemical (China).2.2 Preparation of CNS/TPU composites
TPU was dissolved in THF at a concentration of 10 wt% by stirring. At the same time, CNS was dispersed in mixed solvent (THF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMF = 14
DMF = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume ratio) by ultrasonication for 6 h to obtain uniform CNS suspension. The CNS suspension was then mixed with TPU solution by stirring. To prevent the aggregation of CNS, the spin flash drying was used to concentrate the mixture. Solution casting was used to prepare the final CNS/TPU composite. The extra solvent was completely removed by drying in vacuum oven for 48 h at 40 °C.
1 by volume ratio) by ultrasonication for 6 h to obtain uniform CNS suspension. The CNS suspension was then mixed with TPU solution by stirring. To prevent the aggregation of CNS, the spin flash drying was used to concentrate the mixture. Solution casting was used to prepare the final CNS/TPU composite. The extra solvent was completely removed by drying in vacuum oven for 48 h at 40 °C.
2.3 Characterizations
The chemical groups of CNS and carbonyl stretching region in CNS/TPU composites were measured by the TENSOR 27 Fourier transform infrared (FTIR) spectrometer (Bruker Optics GmbH, Germany) with the attenuated total reflection (ATR) technique. The angle of incidence was set at 45° by using a ZnSe crystal. The operating conditions were 4 cm−1 resolution with 32 scans.The morphology of CNS particles was investigated by a transmission electron microscope (H-800-1, Hitachi Co., Japan). The TEM sample was prepared at 100 °C with a Reichert-Jung Ultracut microtome (Leica Camera AG, Germany) and mounted onto a 200-mesh copper grid. Scanning electron microscope (SEM, S-4800, Hitachi Co., Japan) was used to characterize the microstructure of CNS/TPU composites and. The samples were platinum-coated by plasma sputtering before SEM observations.
The crystallization behavior of pure TPU and CNS/TPU composites were studied by a Differential Scanning Calorimetry (DSC) (STARe, METTLER-TOLEDO, Switzerland) under N2 gas atmosphere. All samples were first heated to 200 °C, and held at that temperature for 10 min to erase the thermal history; then cooled to −100 °C with a cooling rate of 10 °C min−1. The samples were heated again from −100 °C to 200 °C. The mass of samples tested was approximately 5 ± 0.2 mg. Each sample was placed in a 40 μL aluminium crucible with perforated lid.
The mechanical properties of the CNS/TPU composite were carried out on a tensile apparatus (Instron 11185, Instron Corporation, USA) at 25 °C with a stretching speed at 20 mm min−1. All samples were cut into the dumbbell shape (20 mm × 4 mm × 0.2 mm). Elastic modulus (Y) was calculated according to the slope of stress–strain curves within 0–5% of strain, which was obtained by a tensile apparatus (Instron 11185, Instron Corporation, USA) at 25 °C at a strain rate of 2 mm min−1.
The conductivity of CNS/TPU composites were measured at high resistivity meter (EST 121, Beijing Huajinghui Co., Ltd., China). ρv is calculated as follows:
| ρv = 4L/(RV × π × d2), |
A circular strain test was carried out to measure the actuation strain without prestrain. The compliant electrodes were fabricated by spraying graphite suspension composed of graphite, silicone oil and curing agent, on the two main surfaces of the film using an airbrush. The dielectric elastomer film was fixed on a circle frame. The strain was defined as the change in the pixel of the electrodes' area divided by the original pixel. The voltage was supplied by a high-voltage direct current generator (DTZH-60, Wuhan Dotek Electric Co., Ltd., China). In order to obtain the change in the pixel of the electrodes' area, a video camera was fixed above the film to capture the actuator plane before and after applying the voltage with the same focal length, and then the captured video pictures were processed with Photoshop software. The planar strain (actuation strain) is calculated according to
| SP = (A − A0)/A0 × 100% | (4) |
3. Results and discussion
3.1 Hydrogen bonding interaction between CNS and TPU
Hydrogen bonding interaction between CNS and TPU was studied by Fourier transform infrared (FTIR) spectrometer, and the results are shown in Fig. 1. The infrared spectrum of pure CNS is shown in Fig. 1(a). The peaks at 1629 cm−1 and 1728 cm−1 represent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of CNS, respectively. The peak at 3200–3600 cm−1 represent the stretching and the vibration of hydroxyl groups (–OH), demonstrating the existence of large numbers of –OH on CNS. The N–H stretching region of TPU is located between 3100 cm−1 and 3500 cm−1, the hydrogen bonded urethane N–H groups centers at approximately 3338 cm−1.36 As shown in Fig. 1(b), the peak of hydrogen bonded N–H group shifts to lower wave number with the increase of CNS, suggesting the formation of strong hydrogen bonds between N–H groups of TPU molecules and –OH groups of CNS. A curve-fitting procedure based on the Gaussian distribution was used to study the change of the C
O groups of CNS, respectively. The peak at 3200–3600 cm−1 represent the stretching and the vibration of hydroxyl groups (–OH), demonstrating the existence of large numbers of –OH on CNS. The N–H stretching region of TPU is located between 3100 cm−1 and 3500 cm−1, the hydrogen bonded urethane N–H groups centers at approximately 3338 cm−1.36 As shown in Fig. 1(b), the peak of hydrogen bonded N–H group shifts to lower wave number with the increase of CNS, suggesting the formation of strong hydrogen bonds between N–H groups of TPU molecules and –OH groups of CNS. A curve-fitting procedure based on the Gaussian distribution was used to study the change of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in TPU with the addition of CNS and the results are shown in Fig. 1(c). The peaks at 1700 cm−1 and 1725 cm−1 represent the hydrogen bonded C
O groups in TPU with the addition of CNS and the results are shown in Fig. 1(c). The peaks at 1700 cm−1 and 1725 cm−1 represent the hydrogen bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups and the free C
O groups and the free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of TPU, respectively.37 With the increase in the content of CNS, the intensity of the peak for the free C
O groups of TPU, respectively.37 With the increase in the content of CNS, the intensity of the peak for the free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups decreases, whereas the intensity of the peak for the hydrogen-bonded C
O groups decreases, whereas the intensity of the peak for the hydrogen-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups increases. The ratio of the peak area of free C
O groups increases. The ratio of the peak area of free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bands to the peak area of hydrogen-bonded C
O bands to the peak area of hydrogen-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bands gradually decreases from 0.88 for pure TPU to 0.81 for the composite with 5 wt% of CNS. Based on FTIR results, the interaction between TPU molecule and CNS is schematically represented in Fig. 2. The –OH groups of CNS can form strong hydrogen bonds with free N–H groups in hard segment of TPU molecules (O–H⋯N) or with free C
O bands gradually decreases from 0.88 for pure TPU to 0.81 for the composite with 5 wt% of CNS. Based on FTIR results, the interaction between TPU molecule and CNS is schematically represented in Fig. 2. The –OH groups of CNS can form strong hydrogen bonds with free N–H groups in hard segment of TPU molecules (O–H⋯N) or with free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in soft segment (O–H⋯O) of TPU. The enthalpy of “O–H⋯N” and “O–H⋯O” is 29 kJ mol−1 and 21 kJ mol−1, respectively, much higher than that of “N–H⋯O” (8 kJ mol−1); thus, “O–H⋯N” and “O–H⋯O” are much easier to be formed than “N–H⋯O” in the dilute solution. The strong hydrogen bonding interaction between CNS and TPU matrix facilitates the formation of good interfacial adhesion between CNS and TPU, and thus the good dispersion CNS in TPU matrix (see below).
O groups in soft segment (O–H⋯O) of TPU. The enthalpy of “O–H⋯N” and “O–H⋯O” is 29 kJ mol−1 and 21 kJ mol−1, respectively, much higher than that of “N–H⋯O” (8 kJ mol−1); thus, “O–H⋯N” and “O–H⋯O” are much easier to be formed than “N–H⋯O” in the dilute solution. The strong hydrogen bonding interaction between CNS and TPU matrix facilitates the formation of good interfacial adhesion between CNS and TPU, and thus the good dispersion CNS in TPU matrix (see below).
 | ||
| Fig. 1 (a) FTIR spectrum of CNS, (b) FTIR spectra of pure TPU and CNS/TPU composites, and (c) fitting curves of the carbonyl stretching region of pure TPU and CNS/TPU composites. | ||
 | ||
| Fig. 2 Schematic representation of the hydrogen bonding: (a) between TPU molecules, and (b) hydrogen bonding between CNS and TPU molecules. | ||
3.2 Dispersion of CNS in TPU matrix
Fig. 3(a) shows the TEM images of CNS. The average diameter of CNS is 100 nm. The dispersion of CNS in TPU matrix and the interfacial adhesion between CNS and TPU were observed by SEM. Good interfacial interaction between CNS and TPU is observed in the cross-section morphologies of all the CNS/TPU composites with 1 wt%, 3 wt% and 5 wt% of CNS, as shown in Fig. 3(b)–(d), respectively. This is ascribed to the hydrogen bonding interaction between –OH groups of CNS and TPU molecules. Meanwhile, a good dispersion of CNS in TPU matrix is observed in all the CNS/TPU composites with 1 wt%, 3 wt% and 5 wt% of CNS. The good dispersion is ascribed to both the good interfacial interaction of CNS/TPU composites and the fast evaporation of solvent by using the spin flash drying technique, which suppresses the aggregation of CNS. | ||
| Fig. 3 (a) TEM images of CNS and tensile-fractured cross-sectional SEM images of (b) 1 wt% CNS/TPU composite, (c) 3 wt% CNS/TPU composite and (d) 5 wt% CNS/TPU composite. | ||
3.3 Effect of CNS on the crystallization behavior of TPU
The effect of CNS on the crystallization behavior of TPU is studied by DSC, and the results are shown in Fig. 4. A melting peak at 56.5 °C is observed in pure TPU, indicating the crystallization of TPU, as reported in previous study.38 The melting peak of TPU shifts to lower temperature (about 34 °C) by adding 1 wt% of CNS, indicating that even a small content of CNS (1 wt%) disrupts the crystallization of TPU. The melting peak disappears for the composites with 3 wt% and 5 wt% of CNS, suggesting that the crystallization of TPU is severely disrupted by adding CNS to 3 wt% and 5 wt%.To further study the effect of CNS on the crystallization behavior of TPU, the crystal morphologies of CNS/TPU composites are observed by SEM, and the results are shown in Fig. 5. Clear spherulite with a diameter of 15 μm is observed for pure TPU, as shown in Fig. 5(a). Both the diameter and regularity of the spherulites decrease with the increase in content of CNS, as shown in Fig. 5(b)–(d), indicating the disruption of crystal structure of TPU. This result agrees well with the DSC result. The crystallization of pure TPU is initiated by the partial alignment of their molecular chains. These aligned chains fold, nucleate and then form lamellae, which finally form large spherulite. The addition of CNS can disrupt the alignment of molecular chains of TPU because of steric effect of CNS and the hydrogen bonding interaction between –OH of CNS and free N–H groups or free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of TPU, thus disrupt the crystallization of TPU, leading to the decrease in melting point of TPU. The disruption of crystallization of TPU by CNS results in the decrease in elastic modulus of CNS/TPU composites (see Section 3.4).
O groups of TPU, thus disrupt the crystallization of TPU, leading to the decrease in melting point of TPU. The disruption of crystallization of TPU by CNS results in the decrease in elastic modulus of CNS/TPU composites (see Section 3.4).
 | ||
| Fig. 5 Cryo-fractured cross-sectional SEM images of (a) pure TPU, (b) 1 wt% CNS/TPU composite, (c) 3 wt% CNS/TPU composite and (d) 5 wt% CNS/TPU composite. | ||
3.4 Mechanical properties of CNS/TPU composites
The stress–strain curves of pure TPU and CNS/TPU composites are shown in Fig. 6. The corresponding tensile strength and the elastic modulus are summarized in Table 1. The tensile strength of pure TPU is 24.6 MPa, much higher than that of traditional DE materials such as silicone elastomer22 and acrylic rubber hydrogenated nitrile-butadiene rubber.39 The tensile strength increases with the increase in content of CNS, indicating the good reinforcing effect of CNS on TPU. Meanwhile, a high elongation at break (>1600%) is obtained for all the samples. Interestingly, the elastic modulus (Y) of TPU first decreases with the increase in content of CNS from 0 wt% to 3 wt% and then increases with the further increase in content of CNS to 5 wt%. The change in Y of TPU by adding CNS is ascribed to the coeffect of disruption of TPU crystallization by CNS and the reinforcing of CNS on TPU. At low content of CNS (1 wt% to 3 wt%), the disruption of crystallization of TPU by CNS dominates, resulting the continuous decrease in Y. With the content of CNS increasing to 4 wt% and 5 wt%, the reinforcing effect of CNS on TPU dominates, which results in the slightly increase in Y. However, the Y of all the CNS/TPU composites is lower than that of pure TPU.| CNS content (wt%) | Dielectric constant at 103 Hz | Dielectric loss tangent at 103 Hz | Tensile strength (MPa) | Elastic modulus Y (MPa) | β = εr/Y (MPa−1) | Breakdown strength (kV mm−1) | Maximal actuation strain (%) | Actuation strain at 6 kV mm−1 (%) | Conductivity (S m−1) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.1 | 0.01 | 24.6 | 3.83 | 1.9 | 25 | 0.9 | 0.05 | 1.86 × 10−12 |
| 1 | 9.1 | 0.08 | 25.5 | 3.12 | 2.9 | 12.5 | 1.0 | 0.4 | 2.34 × 10−10 |
| 2 | 10.4 | 0.11 | 26.3 | 3.09 | 3.4 | 12 | 1.5 | 0.7 | 4.26 × 10−10 |
| 3 | 11.0 | 0.11 | 27.6 | 2.47 | 4.5 | 12 | 3.2 | 0.9 | 6.67 × 10−10 |
| 4 | 21.0 | 0.47 | 34.7 | 2.87 | 7.3 | 9.8 | 2.1 | 1.2 | 6.76 × 10−10 |
| 5 | 137.3 | 0.91 | 35.4 | 3.50 | 39.2 | 6.3 | 2.4 | 2.4 | 2.51 × 10−7 |
The cyclic stress–strain curves of pure TPU and CNS/TPU composites and the corresponding hysteresis loss at 10% of strain are shown in Fig. 7. The hysteresis loss is originated from the intra-macromolecular friction between TPU chains and the interfacial friction between CNS and TPU during stretching. The hysteresis loss first decreases from 30.2% for pure TPU to 18.3% and 15.3% for the composite with 1 wt% and 3 wt% of CNS, respectively, as shown in Fig. 7(b). In this case, the interfacial friction between CNS and TPU during stretching is relatively small because of the low content of CNS (1 wt% to 3 wt%). Meanwhile, the disruption of crystallization of TPU by CNS increases the chain mobility of TPU, and thus decreases the intra-macromolecular friction between TPU chains during stretching, resulting in the decrease in hysteresis loss. The hysteresis loss then increases to 28.3% for the composite with 5 wt% of CNS, still lower than that of pure TPU. In this case, the interfacial friction between CNS and TPU are largely increased with the content of CNS increasing to 5 wt%, leading to the much larger hysteresis loss of the composite with 5 wt% of CNS than that of the composites with 1 wt% and 3 wt% of CNS. However, the disruption of crystallization of TPU by 5 wt% of CNS can decrease the hysteresis loss of TPU, leading to the lower hysteresis loss of the composite with 5 wt% of CNS than that of pure TPU.
3.5 Electromechanical properties of CNS/TPU composites
The dielectric properties of pure TPU and CNS/TPU composites as a function of frequency are shown in Fig. 8, and the dielectric constant and dielectric loss at 103 Hz are summarized in Table 1. The dielectric constant at the same frequency increases with the increase in content of CNS, as shown in Fig. 8(a). εr is almost independent of the frequency when the content of CNS (1 wt% to 3 wt%) is below the percolation threshold. A great increase in εr at low frequencies is observed as the content of CNS reaches the percolation threshold (4 wt% and 5 wt%). For example, the dielectric constant at 103 Hz increases from 7.1 for pure TPU to 21 and 137.3 for the composite with 4 wt% and 5 wt% of CNS, respectively. Two reasons are responsible for the significant increase in dielectric constant. One is the accumulation of a large number of interfacial charges at the interface between CNS and TPU, which is known as interfacial polarization effect or Maxwell–Wagner–Sillars (MWS) effect.40,41 The second reason is the good dispersion of CNS in TPU matrix (see Section 3.1) and the formation of conductive network as the content of CNS reaches the percolation threshold (4 wt%).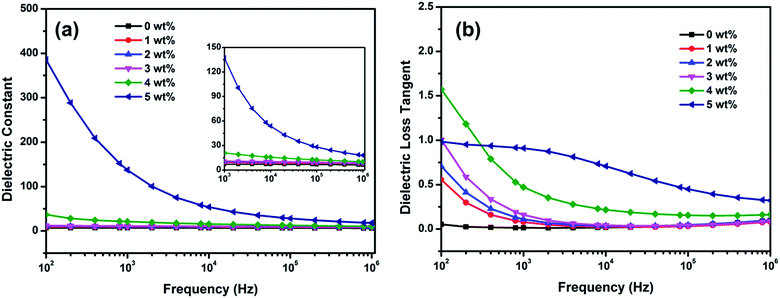 | ||
| Fig. 8 Dielectric properties of CNS/TPU composites: (a) dielectric constant, and (b) dielectric loss tangent of TPU and CNS/TPU composites. | ||
Meanwhile, the dielectric loss of all the composites also shows a strong frequency dependence in low frequencies (102 Hz to 103 Hz) and a weak frequency dependence in high frequencies (103 Hz to 106 Hz), as shown in Fig. 8(b). The dielectric loss at 103 Hz remains at low values (0.01–0.47) for the composites with 1 wt% to 4 wt% of CNS, ascribed to the low DC conductivity of these composites, as demonstrated by the low electrical conductivity (<10−9 S m−1) of these composites (see Table 1). The dielectric loss at 103 Hz obviously increases to 0.91 for the composite with 5 wt% of CNS because of the increase in DC conductivity, as demonstrated by the obviously increased electrical conductivity (2.51 × 10−7 S m−1) (see Table 1). The dielectric loss at 103 Hz of all these samples is less than 1, facilitating the application of these dielectric composites.
The electromechanical sensitivity (β) of pure TPU and CNS/TPU composites are summarized in Table 1. We can observe that β slightly increases with the content of CNS increasing from 0 wt% to 4 wt%, mainly attributed to the slight increase in εr and decrease in Y with increasing the content of CNS. β greatly increases to 39.2 with the further increase in content of CNS to 5 wt%, a 20-fold increase over that of pure TPU (1.9). This is ascribed to the great increase in εr of TPU by adding 5 wt% of CNS. The great increase in β facilitates the great increase in actuation strain of CNS/TPU composites at a low electric field (see below).
Fig. 9 shows the actuation strain as a function of electric field for pure TPU and CNS/TPU composites. The values of the breakdown strength, the maximum actuation strain and the actuation strain at 6 kV mm−1 are summarized in Table 1. Before breakdown, the actuation strain at the same electric field is obviously increased with the increase in content of CNS. For example, the actuation strain at 6 kV mm−1 increases from 0.05% for pure TPU to 2.4% for the composite with 5 wt% of CNS, indicating 48-fold increase in actuation strain by the addition of 5 wt% of CNS. The large increase in actuation strain is ascribed to the large increase in β caused by the great increase in εr and the decrease in Y by adding 5 wt% of CNS. The breakdown strength decreases from 25 kV mm−1 for pure TPU to 12 kV mm−1 for the composites with 1 wt% to 3 wt% of CNS and it further decreases to 6.3 kV mm−1 for the composite with 5 wt% of CNS, ascribed to the increase in DC conductance caused by the increase in the conductivity of CNS/TPU composites (see Table 1). As a result, the maximum actuation strain (3.2% at 12 kV mm−1) is obtained for the composite with 3 wt% of CNS, which is much higher than that of pure TPU (0.9% at 25 kV mm−1).
The history dependence, as an important property of DEAs, was also studied. As an example, the actuation strain of the composite with 3 wt% of CNS was measured for 10 cycles, and the results are shown in Fig. 10. The electric field of 6 kV mm−1 was applied periodically; each application period of 10 seconds was followed by an off-interval of 3 seconds. We can observe that the actuation strain (1.48 ± 0.11%) is stable with time, a desirable feature of CNS/TPU composite in DEA applications.
4. Conclusion
CNS/TPU dielectric composites with good mechanical strength, high dielectric constant, and largely improved actuation strain at low electric field were successfully prepared. The hydroxyl groups on the surface of CNS can form strong hydrogen bonds with the free N–H groups in hard segment of TPU molecules or with the free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in soft segment of TPU. As a result, a good interface adhesion between CNS and TPU matrix, a good dispersion of CNS in TPU matrix, and the obviously improved tensile strength of the CNS/TPU composites were obtained. CNS disrupted the crystal structure of TPU, decreasing the elastic modulus and hysteresis loss of CNS/TPU composites. Meanwhile, the addition of CNS increased the dielectric constant at 103 Hz from 7.1 for pure TPU to 137.3 for the composite with 5 wt% of CNS. The simultaneous increase in dielectric constant and decrease in elastic modulus result in 48-fold increase in actuation strain at low electric field (6 kV mm−1) by adding 5 wt% of CNS. The maximum actuation strain (3.2% at 12 kV mm−1) obtained for the composite with 3 wt% of CNS is much higher than that of pure TPU (0.9% at 25 kV mm−1). Meanwhile, a low dielectric loss at 103 Hz was obtained in all the as-prepared CNS/TPU composites. This study provides a simple and effect way to obtain TPU dielectric elastomer with good mechanical strength and largely improved actuation performance at low electric field for its wide application.
O groups in soft segment of TPU. As a result, a good interface adhesion between CNS and TPU matrix, a good dispersion of CNS in TPU matrix, and the obviously improved tensile strength of the CNS/TPU composites were obtained. CNS disrupted the crystal structure of TPU, decreasing the elastic modulus and hysteresis loss of CNS/TPU composites. Meanwhile, the addition of CNS increased the dielectric constant at 103 Hz from 7.1 for pure TPU to 137.3 for the composite with 5 wt% of CNS. The simultaneous increase in dielectric constant and decrease in elastic modulus result in 48-fold increase in actuation strain at low electric field (6 kV mm−1) by adding 5 wt% of CNS. The maximum actuation strain (3.2% at 12 kV mm−1) obtained for the composite with 3 wt% of CNS is much higher than that of pure TPU (0.9% at 25 kV mm−1). Meanwhile, a low dielectric loss at 103 Hz was obtained in all the as-prepared CNS/TPU composites. This study provides a simple and effect way to obtain TPU dielectric elastomer with good mechanical strength and largely improved actuation performance at low electric field for its wide application.
Acknowledgements
We would like to express our sincere thanks to the National Natural Science Foundation of China (Grant no. 51173007, and 51221002) for financial support.References
- R. Pelrine, R. Kornbluh and G. Kofod, Adv. Mater., 2000, 12, 1223–1225 CrossRef CAS.
- G. Ouyang, K. Wang and X. Chen, J. Micromech. Microeng., 2012, 22, 074002 CrossRef.
- Y. Jang and T. Hirai, Soft Matter, 2011, 7, 10818–10823 RSC.
- R. Shankar, T. K. Ghosh and R. J. Spontak, Soft Matter, 2007, 3, 1116–1129 RSC.
- Q. Pei, M. A. Rosenthal, R. Pelrine, S. Stanford and R. D. Kornbluh, Smart Structures and Materials, International Society for Optics and Photonics, 2003, pp. 281–290 Search PubMed.
- M. Aschwanden and A. Stemmer, Opt. Lett., 2006, 31, 2610–2612 CrossRef.
- A. O'Halloran, F. O'Malley and P. McHugh, J. Appl. Phys., 2008, 104, 071101 CrossRef PubMed.
- L. Z. Chen, C. H. Liu, C. H. Hu and S. S. Fan, Appl. Phys. Lett., 2008, 92, 263104 CrossRef PubMed.
- F. Carpi, G. Gallone, F. Galantini and D. De Rossi, Adv. Funct. Mater., 2008, 18, 235–241 CrossRef CAS.
- C. Huang and Q. Zhang, Adv. Funct. Mater., 2004, 14, 501–506 CrossRef CAS.
- H. Stoyanov, M. Kollosche, S. Risse, D. N. McCarthy and G. Kofod, Soft Matter, 2011, 7, 194 RSC.
- M. Molberg, Y. Leterrier, C. J. Plummer, C. Walder, C. Löwe, D. M. Opris, F. A. Nüesch, S. Bauer and J.-A. E. Månson, J. Appl. Phys., 2009, 106, 054112 CrossRef PubMed.
- F. Carpi, S. Bauer and D. De Rossi, Science, 2010, 330, 1759–1761 CrossRef CAS PubMed.
- I. Krakovský, T. Romijn and A. P. de Boer, J. Appl. Phys., 1999, 85, 628–629 CrossRef PubMed.
- S. A. Harich, D. Dai, C. C. Wang, X. Yang, S. D. Chao and R. T. Skodje, Nature, 2002, 419, 284–287 CrossRef PubMed.
- S. Risse, B. Kussmaul, H. Krüger and G. Kofod, Adv. Funct. Mater., 2012, 22, 3958–3962 CrossRef CAS.
- H. Stoyanov, M. Kollosche, D. N. McCarthy and G. Kofod, J. Mater. Chem., 2010, 20, 7558 RSC.
- P. Brochu and Q. Pei, Macromol. Rapid Commun., 2010, 31, 10–36 CrossRef CAS PubMed.
- F. Carpi and D. D. Rossi, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 835–843 CrossRef CAS.
- Z.-M. Dang, H.-P. Xu and H.-Y. Wang, Appl. Phys. Lett., 2007, 90, 012901 CrossRef PubMed.
- F. Galantini, S. Bianchi, V. Castelvetro and G. Gallone, Smart Mater. Struct., 2013, 22, 055025 CrossRef.
- M. Tian, Z. Wei, X. Zan, L. Zhang, J. Zhang, Q. Ma, N. Ning and T. Nishi, Compos. Sci. Technol., 2014, 99, 37–44 CrossRef CAS PubMed.
- J. Xu, M. Wong and C. Wong, Electronic Components and Technology Conference, 2004, Proceedings, 54th, IEEE, 2004, vol. 1, pp. 536–541 Search PubMed.
- H. Stoyanov, M. Kollosche, S. Risse, R. Wache and G. Kofod, Adv. Mater., 2013, 25, 578–583 CrossRef CAS PubMed.
- D. M. Opris, D. Crespy, C. Löwe, M. Molberg and F. Nüesch, International Society for Optics and Photonics, 2009, 7287, 72870L Search PubMed.
- A. Nieto-Márquez, R. Romero, A. Romero and J. L. Valverde, J. Mater. Chem., 2011, 21, 1664 RSC.
- G. E. Poinern, S. Brundavanam, M. Shah, I. Laava and D. Fawcett, Nanotechnol., Sci. Appl., 2012, 5, 49–59 CrossRef CAS PubMed.
- D. Yuan, J. Chen, J. Zeng and S. Tan, Electrochem. Commun., 2008, 10, 1067–1070 CrossRef CAS PubMed.
- M. Tian, Q. Ma, X. Li, L. Zhang, T. Nishi and N. Ning, J. Mater. Chem. A, 2014, 2, 11144–11154 CAS.
- N. Karak, R. Konwarh and B. Voit, Macromol. Mater. Eng., 2010, 295, 159–169 CAS.
- C. Triebel, S. Vasylyev, C. Damm, H. Stara, C. Özpınar, S. Hausmann, W. Peukert and H. Münstedt, J. Mater. Chem., 2011, 21, 4377–4383 RSC.
- K. Wongtimnoi, B. Guiffard, A. Bogner-Van de Moortèle, L. Seveyrat, C. Gauthier and J. Y. Cavaillé, Compos. Sci. Technol., 2011, 71, 885–892 CrossRef CAS PubMed.
- C. Prisacariu, Polyurethane elastomers: from morphology to mechanical aspects, Springer, Science & Business Media, 2011, ch. 2, pp. 35–42 Search PubMed.
- H. Tanaka and M. Kunimura, Polym. Eng. Sci., 2002, 42, 1333–1349 CAS.
- M. Chen, L. Bin, H.-h. Song and L.-j. Zhi, New Carbon Mater., 2010, 25, 199–204 CrossRef.
- M. Tian, B. Yan, Y. Yao, L. Zhang, T. Nishi and N. Ning, J. Mater. Chem. C, 2014, 2, 8388–8397 RSC.
- M. M. Coleman, D. J. Skrovanek, J. Hu and P. C. Painter, Macromolecules, 1988, 21, 159–165 CrossRef.
- M. F. Sonnenschein, Z. Lysenko, D. A. Brune, B. L. Wendt and A. K. Schrock, Polymer, 2005, 46, 10158–10166 CrossRef CAS PubMed.
- D. Yang, L. Zhang, N. Ning, D. Li, Z. Wang, T. Nishi, K. Ito and M. Tian, RSC Adv., 2013, 3, 21896 RSC.
- G. Gallone, F. Carpi, D. De Rossi, G. Levita and A. Marchetti, Mater. Sci. Eng., C, 2007, 27, 110–116 CrossRef CAS PubMed.
- D. Mc Carthy, S. Risse, P. Katekomol and G. Kofod, J. Phys. D: Appl. Phys., 2009, 42, 145406 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |





