Microscopic origin of MXenes derived from layered MAX phases
Abstract
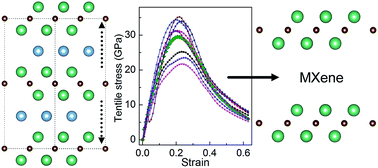
Two-dimensional transition metal carbides/nitrides Mn+1Xns labeled as MXenes derived from layered transition metal carbides/nitrides referred to as MAX phases attract increasing interest due to their promising applications as Li-ion battery anodes, hybrid electro-chemical capacitors and electronic devices. To predict the possibility of forming various MXenes, it is necessary to have a full understanding of the chemical bonding and mechanical properties of MAX phases. In this work, we investigated the chemical bonding changes of MAX phases in response to tensile and shear stresses by ab initio calculations using M2AlC (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo and W) as examples. Our results show that the M2C layer is likely to separate from the Al layer during the tensile deformation, where the failure of M2AlC is characterized by an abrupt stretch of the M–Al bonds. While under shear deformation, the M2C and Al layers slip significantly relative to each other on the (0001) basal planes. It is found that the ideal strengths of M2AlC are determined by the weak coupling of the M2C and Al layers, closely related to the valence-electron concentration. Our results unravel the possibility as well as the microscopic mechanism of the fabrication of MXenes through mechanical exfoliation from MAX phases.

 Please wait while we load your content...
Please wait while we load your content...