Optimisation of the process variables in production of activated carbon by microwave heating

Abstract

This study aims to investigate the optimal operating conditions in order to obtain cost effective production of activated carbon (AC) from palm kernel shell (PKS) by microwave heating. Interactions among the independent variables, namely irradiation time (T), microwave power (W), impregnation ratio between impregnating substances and PKS, and the concentration of impregnating substance (sulphuric acid) were considered for optimising the process parameters during the production of AC, aided by Central Composite Design. The optimum conditions for the independent process variables were 11.02 minutes of irradiation time, microwave power of 676 W and impregnation ratio of 0.68. The AC produced in this work had a surface area of 1011 m² g⁻¹ with high porosity as shown by scanning electron microscopy (SEM). Zinc was used to verify the potential of AC as an adsorbent. Zinc removal at the optimum conditions was found to be 13.72 mg g⁻¹. Such a Zn removal value is comparable with the earlier work of other researchers who used a conventional way of producing the AC. It is believed that microwave technology can be used for the production of AC in a short time with high energy efficiency, e.g., 11 minutes against 2–5 hours of reactivation for conventional methods.

---

1. Introduction

Activated carbon (AC) is a unique and versatile adsorbent that has been used since the ancient times by Egyptians and Indians for removal of unwanted odour, taste, dyes, heavy metals and organic substances. In modern times, it has been widely used by the chemical industry for removal, separation and pre-concentration of both metallic and organic species from water and waste water.^1–3 There have been persistent efforts to prepare AC from low cost materials⁴ to reduce the production cost. However, the cost of energy for the production of AC remains a concern. A typical production process of the AC requires heating the carbonaceous materials for one to seven hours to convert them into porous AC.^5–9 The requirement for this long heating time may be due to the fact that, heating occurs through convection, conduction, and radiation of thermal energy from the surface of the material towards the core. This creates a bottleneck in the manufacturing process.

Thus, the objective of this study was to investigate the optimal operating conditions for cost effective production of AC. The important factors that contribute to production cost are heating time as well energy and chemical use. The use of microwave technology could facilitate cost effective production,^10,11 as in the case of microwave heating, the thermal energy is produced due to molecular interaction with the microwave energy. The microwave penetrates the material and the microwave energy is converted to thermal energy. Thus, heat is generated throughout the bulk of the material and distribute more efficiently within the material. This can reduce the processing time and improve the overall product quality.¹²

Response surface methodology (RSM) is a collection of mathematical and statistical techniques which aid the analysis of experimental data and the optimisation of the result within a given range of operating parameters.¹³ A Box-Wilson Central Composite Design, more familiar by the name of central composite design (CCD), is one of the most popular response surface methodology (RSM) designs due to the advantages that, CCDs are very efficient in providing important information on effects of the experimental variables and experimental error in a minimum number of experimental runs. The flexibility of CCDs allows studying different experimental regions of interest and operability conditions with the help of several varieties of CCD.^14–16

In the conventional one-factor-at a time experiments, number of experiments are very large as well as, no interaction effects are studied. However, in RSM, reaction parameters can be varied simultaneously as required to generate data and that data can be used to propose an empirical model. This makes the RSM a better economical and quick analytical approach towards optimisation than the conventional approach.¹⁷ Hence, CCD and RSM methods were used in this study to determine the optimum operating conditions. Palm kernel shells (PKS) were used in this study as the raw material as this material is widely available as agricultural waste in Malaysia. This raw material was impregnated with sulphuric acid. Zinc was chosen as model adsorbate as a response to find out the effectiveness of the AC. Zinc is a carcinogenic heavy metal, and it causes internal organ damage and death to human being if taken in excessive dose. It is also harmful to the aquatic ecosystems.^18–20 To understand the physical character of the produced AC at the optimum conditions, scanning electron micrograph (SEM) imaging, Fourier transform infrared spectroscopy (FTIR) and BET surface area were used in this study.

2. Methodology

2.1. Materials used in the preparation of AC

Palm kernel shells (PKS) obtained from a local palm oil mill were washed to remove dust and dried in an oven at 105 °C until its mass became constant. Sulphuric acid and zinc nitrate used in this study were of analytical grade and obtained from R&M chemicals, Malaysia and Fluka Chemicals, UK. All solutions were prepared in distilled water. A stock solution of Zn(II) of concentration 1000 mg L⁻¹ was prepared with zinc nitrate. The desired concentrations were prepared by dilution method from the stock solution with distilled water.

2.2. Design of experiment

A CCD method was chosen so that a quadratic surface could be fitted to the response with minimum number of experiments. It was believed that the interaction between the effective process parameters could be identified and finally, the combination of operating parameters would be identified to optimise the response. The most effective parameters namely, irradiation time (T) coded as Factor A, microwave power (P) coded as Factor B, impregnation ratio (IR) coded as Factor C and sulphuric acid concentration coded as Factor D, responsible for the quality of the AC were taken at various levels as marked in Table 1. It shows the ranges and the levels of independent variables in this study. Here the low actual values of the factors were coded as −1 and the high actual values were coded as +1.

Table 1 Summary of experimental design of preparation of AC

Factor	Name	Units	Type	Low actual	High actual	Low coded	High coded	Mean
A	Time	Min	Numeric	5	20	−1	1	12.5
B	Power	W	Numeric	600	1000	−1	1	800
C	IR		Numeric	0.5	2	−1	1	1.25
D	Conc. of acid	%	Numeric	20	100	−1	1	60

---

The total number of runs in CCD consisted of factorial runs, axial runs and centre runs. Eqn (1) gives the number of total runs required to fit the quadratic surface where n is number of independent variables.

N = 2ⁿ + 2n + n_c (1)

In this study, a face-centred CCD for four variables, consisting of 16 factorial points, eight axial points and four replicates at the centre points with a total number of 28 experiments was applied to find the optimum condition. The four replicate experiments at centre point were used for estimating the experimental error and the duplicability of the data. Table 2 shows the different combinations of the independent variables suggested by the Design Expert software (version 7.1.6, Stat-Ease, Inc.)^21,22 as well as the response for each run.

Table 2 Experimental matrix for the preparation of AC and the response in terms of adsorption and yield

Std	Run	Type	Factor 1	Factor 2	Factor 3	Factor 4	Adsorption (mg g^−1)	Yield (%)
			A: time min	B: power W	C: IR	D: conc. of acid%
4	1	Fact	20	1000	0.5	20	1.305	90.17
6	2	Fact	20	600	2	20	4.895	58.65
28	3	Center	12.5	800	1.25	60	12.599	62.25
21	4	Axial	12.5	800	0.5	60	11.568	77.61
22	5	Axial	12.5	800	2	60	14.6955	49.7
1	6	Fact	5	600	0.5	20	3.445	93.64
9	7	Fact	5	600	0.5	100	6.9585	97.3
10	8	Fact	20	600	0.5	100	9.9105	68.62
16	9	Fact	20	1000	2	100	5.852	31.26
24	10	Axial	12.5	800	1.25	100	14.807	69.99
17	11	Axial	5	800	1.25	60	7.7605	78.59
8	12	Fact	20	1000	2	20	5.265	53.19
20	13	Axial	12.5	1000	1.25	60	11.8895	44.91
7	14	Fact	5	1000	2	20	6.905	85.03
11	15	Fact	5	1000	0.5	100	3.5015	66.06
26	16	Center	12.5	800	1.25	60	14.112	61.99
5	17	Fact	5	600	2	20	6.21	82.85
27	18	Center	12.5	800	1.25	60	14.787	48.95
19	19	Axial	12.5	600	1.25	60	14.6085	59.06
18	20	Axial	20	800	1.25	60	11.9525	51.15
23	21	Axial	12.5	800	1.25	20	12.285	74.73
25	22	Center	12.5	800	1.25	60	14.666	48.86
14	23	Fact	20	600	2	100	12.9625	39.45
2	24	Fact	20	600	0.5	20	5.14	82.94
3	25	Fact	5	1000	0.5	20	3.115	94.74
15	26	Fact	5	1000	2	100	8.958	70.66
13	27	Fact	5	600	2	100	4.926	91.28
12	28	Fact	20	1000	0.5	100	5.443	53.76

---

Yield of AC (y₁) and the adsorption of zinc (y₂) were taken as the response of the processes. ANOVA, regression analysis and the interaction among the parameters were also studied. A second order polynomial eqn (2) was used to model the relation between the process variables and the response.^23,24

where, y is the response or dependent variable, i and j are linear and quadratic coefficients, respectively; β is the regression coefficient; k is the number of factors studied and optimised in the experiment; ε is the random error.

2.3. Preparation of the adsorbent

The raw material was grinded to 1000–2000 μm size and washed thoroughly with distilled water. The grinded PKSs were impregnated with different concentration of sulphuric acid at different impregnation ratios. Undiluted sulphuric acid was considered as 100% that was subsequently diluted as per requirement. Twenty grams of the precursor was mixed with the required amount of acid for four hours with constant stirring at 120 rpm at room temperature. The slurry was then dried in a vacuum oven at 100 °C for 24 h. A microwave furnace with frequency 2450 MHz (SYNOTHERM corporation, model: HAMiLab-C) was used for heating purpose. The impregnated and dried samples were placed in a specially designed quartz tube, which was placed vertically in the microwave oven for the required length of time and at the required microwave power, based on the experimental design. The quartz tube was purged with nitrogen gas at a flow of 0.4 L m⁻¹ for 5 minutes before microwave treatment to outgas air. This flow rate was maintained during the activation and cooling stages. The product obtained was then washed thoroughly with distilled water until the pH of the washing solution reached a value between 5 and 6.

2.4. Experimental work

Batch adsorption experiments were conducted to eliminate volume correction. Experiments were performed in 250 mL Erlenmeyer flasks containing 100 mL of the solution and constantly agitated at 120 rpm until equilibrium was reached. All adsorption experiments were performed at pH 5 to eliminate the chance of precipitation. Hydrochloric acid was used to maintain the pH of the solution.

After the reaction, all samples were filtered with ‘Filtres Fioroni 601’ filter paper and the final concentration of zinc was measured with ICP-OES (Perkin-Elmer 7000DV). The following equation was applied to calculate the final concentration of zinc,

where, C₀ and C_e are the initial and final concentrations of zinc at equilibrium in mg L⁻¹, respectively; m is mass of adsorbent in gram (g) and V is volume of solution in L.

2.5. Characterisation of the surface

The pore structures of the prepared AC were analysed using N₂ adsorption and scanning electron microscopy (SEM). Nitrogen adsorption/desorption isotherms were used to measure the BET surface area, total pore volume and pore size distribution at 77 K by a Quantachrome Autosorb-6B. Field Emission Scanning Electron Microscopy (FESEM) (Brand Zeiss Model Auriga) was employed to study the surface morphology and pore development. Fourier transform infrared (FTIR) spectroscopy was carried out to analyse the surface functional groups of the precursor material and the prepared AC with the help of Bruker, IFS66v/S. Spectra are recorded at a range of 400 to 4000 cm⁻¹. These analyses were performed following the method mentioned by Acharya et al.²⁵ The size of the particles of the AC was measured by Malvern Mastersizer 2000. The instrument used laser diffraction technology based on the principle that laser scattering occurs when it hits a particle and the angle of scattering is directly related to the particle size.

3. Results and discussion

3.1. Statistical analysis and model development

Statistical analysis of the data obtained for zinc adsorption and the yield of the twenty eight different samples, prepared according to the design matrix, were analysed with the aid of Design Expert software. Data for adsorption of zinc can also be better fitted to the quadratic model. The adjusted R² value for the quadratic model for zinc adsorption is 0.8840, which is superior to the R² value of linear, 2FI and cubic polynomial model having R² value 0.0082, −0.2242, and 0.8435, respectively. For the yield of AC, the response was fitted to linear, two-factor interaction (2FI), quadratic and cubic polynomials to determine the most suitable model. The model fit summary showed that the quadratic model was a better fit for the data obtained as the adjusted R² value for the quadratic model for yield of AC was 0.8889, much closer to unity than the R² values of linear (0.5772), 2FI (0.6494) and cubic polynomials (0.8642). The respective p-values for quadratic, linear, 2FI and cubic were 0.8083, 0.2326, 0.2802, and 0.6830, that also suggests quadratic type as the most suitable model. The quadratic model equation for the yield of AC and the zinc adsorption in terms of the coded factors are given in the eqn (4) and (5):

Adsorption = 14.26 + 0.61A − 0.93B + 1.13C + 1.38D − 1.00AB − 0.18AC + 0.81AD + 0.63BC − 0.49BD − 4.98A² − 1.58B² − 1.70C² (4)

Yield = 57.92 − 12.83A − 4.67B − 9.04C − 7.09D + 1.71AB − 5.69AC − 3.81AD + 0.36BC − 5.0BD + 1.79CD + 5.34A² − 7.54B² + 4.13C² + 12.83D² (5)

ANOVA is an important tool, which tests the significance of the differences between means, thereby helps to understand the significance of a model.²⁶ ANOVA determines the impact of the independent variables on the dependent variables in a regression analysis. As shown in Table 3, ANOVA of the regression models shows that the quadratic type to be highly significant for assessing the metal ions removal. This is evident from the Fisher's F-test where the F_{model,adsorption} = 18.82 and F_model,yield = 16.43, with a very low probability value of P model > F = 0.0001 for both the adsorption and yield. There was only a 0.01% chance that a model value of this magnitude could occur due to noise. In the graph of the predicted values versus actual data points, the 45 degree line should evenly split the data set. In this case, it is clear that from Fig. 1(A) and (B), the points are evenly distributed around the 45 degree line. This observation suggests that the model can closely predict the response.

Table 3 ANOVA of regression models for adsorption and yield

	Response	Adsorption
ANOVA for response surface reduced quadratic model
Source	Sum of squares	df	Mean square	F value	p-value prob. > F
Model	479.06	12	39.92	18.82	<0.0001	Significant
A-time	6.66	1	6.66	3.14	0.0968
B-power	15.72	1	15.72	7.41	0.0157
C-IR	22.85	1	22.85	10.78	0.005
D-conc. of acid	34.04	1	34.04	16.05	0.0011
AB	15.97	1	15.97	7.53	0.0151
AC	0.49	1	0.49	0.23	0.6373
AD	10.39	1	10.39	4.9	0.0428
BC	6.35	1	6.35	2.99	0.1042
BD	3.9	1	3.9	1.84	0.195
A^2	69.74	1	69.74	32.88	<0.0001
B^2	7.07	1	7.07	3.33	0.0879
C^2	8.15	1	8.15	3.84	0.0688
Residual	31.81	15	2.12
Lack of fit	28.78	12	2.4	2.37	0.2589	Not significant
Pure error	3.03	3	1.01
Cor total	510.88	27
R^2 = 0.9377, adj. R^2 = 0.8879, pred. R-squared = 0.6997, adeq. precision = 14.342

---

	Response	Yield
ANOVA for response surface quadratic model
Source	Sum of squares	df	Mean square	F value	p-value Prob. > F
Model	8478.74	14	605.62	16.43	<0.0001	Significant
A-time	2963.47	1	2963.47	80.38	<0.0001
B-power	392.09	1	392.09	10.63	0.0062
C-IR	1471.89	1	1471.89	39.92	<0.0001
D-conc. of acid	903.98	1	903.98	24.52	0.0003
AB	46.58	1	46.58	1.26	0.2813
AC	517.79	1	517.79	14.04	0.0024
AD	231.8	1	231.8	6.29	0.0262
BC	2.02	1	2.02	0.055	0.8187
BD	399.6	1	399.6	10.84	0.0058
CD	51.41	1	51.41	1.39	0.2588
A^2	73.58	1	73.58	2	0.1812
B^2	146.81	1	146.81	3.98	0.0674
C^2	43.91	1	43.91	1.19	0.295
D^2	424.65	1	424.65	11.52	0.0048
Residual	479.3	13	36.87
Lack of fit	304.62	10	30.46	0.52	0.8083	Not significant
Pure error	174.67	3	58.22
Cor total	8958.04	27
R^2 = 0.9465, adj. R^2 = 0.8889, pred. R-squared 0.7671, adeq. precision = 15.133

---

Fig. 1 Predicted vs. actual plot for (A) adsorption of Zn and (B) yield of AC.

Predicted R² is an indication of the accuracy of the prediction of a response value by the model. Predicted R² can prevent over-fitting the model and can be more useful than adjusted R² for comparing models because it is calculated using observations not included in model estimation. A difference of 0.20 or less between adjusted R² and predicted R² is considered acceptable for the model to sufficiently predict the response. In the case of adsorption, the predicted R² value was 0.6997, which was within reasonable agreement with the adjusted R² value of 0.8879. In case of yield too, the predicted R² was in reasonable agreement with the adjusted R² as evident from the ANOVA table (Table 3). Adequate precision measures the signal to noise ratio, which indicates the preciseness of the model. A ratio greater than 4 is desirable. Signal to noise ratio of 14.342 in case of adsorption and 15.133 for yield of AC are considered adequate for this purpose. Thus, this model can be used to navigate in the design space. The influence of the ith observation on the fitted value in standard deviation units can be observed by the DFFITS. The DFFITS plot for zinc adsorption in Fig. 2(A) and (B) shows that only 3 data are outliers as these are outside the calculated limits. The DFFITS plot for yield in Fig. 2(B) shows that only 2 data were outliers.

Fig. 2 DFFITS plot for (A) zinc adsorption (B) yield of activated carbon.

3.2. Effect of multiple variables during in preparation of AC for the adsorption of Zn

The variables, namely irradiation time (T), microwave power (P), impregnation ratio (IR) and concentration of acid and the interaction between these variables determine the quality of the AC during production. ANOVA in Table 3 shows that P, IR, and concentration of acid to be very important factors as the p-value is less than 0.05.

3.2.1. Combined effect of irradiation time and microwave power. The interaction of the irradiation time and the microwave power can be observed in the three dimensional interaction plots of the variables given in Fig. 3(A). At the lower value, such as 5 min and 600 W, respectively, produced AC had much less adsorption capacity (6.3 mg L⁻¹). Increase in the irradiation time and microwave power led to the better quality of AC in terms of its adsorption capacity. The adsorption capacity of the AC produced at 12.5 min of irradiation time and 800 W of microwave power reached around 14 mg L⁻¹. However, after this level, the adsorption capacity of the produced AC again decreased. The reason for such adsorption trend may be attributed to incomplete conversion of the impregnated material to AC due to insufficient irradiation time and energy in the lower levels. When the irradiation time and the microwave power were at the higher end, the interaction between these factors led to the destruction of the pore structure and burning off of carbon due to over exposure and excessive energy²⁷ and thus the lack of adsorption site could not facilitate high adsorption capacity of the AC.

Fig. 3 Three dimensional graphical representation of the interaction between (A) time and power, (B) time and IR, (C) power-IR, and (D) time and concentration of acid for Zn adsorption.

3.2.2. Combined effect of irradiation time and impregnation ratio. It was observed that as the impregnation ratio (quantity of acid: quantity of PKSs) was increased the adsorption capacity was increased at first but then decreased after a certain level. This trend was observed when interaction between time and impregnation ratio (Fig. 3(B)) was studied. Lower levels as well as higher levels of impregnation ratio and irradiation time produced AC with low adsorption capacity of only 5.6 mg L⁻¹. At lower level of impregnation ratio, the amount of acid was too small to react with the amount of raw material adequately; therefore, the development of the micro and meso pores was not facilitated. At the high impregnation ratio, the excess amount of sulphuric acid could break down the lignocellulose structure of the palm kernel shell and therefore the pore formation was not possible. It was reflected in the low adsorption capacity of the AC.

3.2.3. Combined effect of impregnation ratio and microwave power. Interactive effect of impregnation ratio and microwave power suggested that at lower impregnation ratio, the adsorption capacity was reduced with increasing power possibly due to higher burning off of the insufficiently impregnated material. Higher impregnation ratio and microwave power also affected the quality of the AC negatively by destroying the pore structure, as can be observed from Fig. 3(C).

3.2.4. Combined effect of acid concentration and irradiation time. The concentration of the acid used for impregnation had a considerable effect on the adsorption capacity of the AC. With the increasing concentration of acid, the adsorption capacity was found to increase (Fig. 3(D)). It was highest when undiluted acid (considered as 100% acid) was used. The cellular structure of palm kernel shells was attacked by the acid, which led to the rupture of the linkages between the lignin and cellulose during the impregnation stage.^28,29 In the next stage, larger structural units and strong cross linked solids were formed by recombination reactions.³⁰ The undiluted acid facilitated this reaction best.

This adsorption behaviours at the lower levels and higher levels of the variables indicated that there exist optimum levels for these variables, which must be found out by optimisation of these factors.

3.3. Effect of multiple variables during the preparation of AC for yield of the AC

Yield of the product obtained from a process is an important factor considering the economic viability of the product. The selected factors T, W, IR and concentration of acid also had important effect on the yield of AC. The interaction of these variables took important role in determining the yield of the AC.

3.3.1. Combined effect of irradiation time and microwave power. At high irradiation time and power, yield of AC was only about 39%, possibly due to burnt off and excessive release of volatile matter and tar present in the raw material.³¹ Whereas, at lower irradiation time and power levels, the yield was higher, about 80%, due to incomplete conversion of the raw material to AC as may be observed from Fig. 4(A).

Fig. 4 Three dimensional graphical representation of the interaction between (A) time and power, (B) time and IR, (C) time and concentration, and (D) IR and conc. of acid for yield of AC.

3.3.2. Combined effect of impregnation ratio and irradiation time. It was also observed that, high impregnation ratio caused yield to decrease from 72% to about 40% when interaction with time was considered as can be seen from Fig. 4(B). At higher impregnation ratio, the cleavage of the lignin cellulose matter occurred in higher proportion and when exposed for longer time, the extent of carbon-chemical reaction increased thereby releasing more volatile matter and tar.^32,33

3.3.3. Combined effect of concentration of acid and irradiation time. Fig. 4(C) shows the trend when the interaction between irradiation time and concentration of acid was considered to assess the yield of the AC. It was observed that at low irradiation time, the yield decreased with increasing concentration of acid and after the acid concentration was more than 80%, the yield increased slightly from 70% to 81% probably due to the reason that very high concentration of acid in the range of 80–100%, may have blocked the pores and hindered the formation of tar,³² therefore resulting in the increase of the yield.

Similar interaction had been observed between impregnation ratio and concentration of acid as shown in Fig. 4(D).

The general trend was the yield of AC decreased with increase in the level of the variables used. This trend was also reported by Xia et al.³⁴ as well as Xin-hui et al.³²

3.4. Optimisation of the preparation of AC

The commercial production of AC demands higher product yield for economic reasons while the adsorption efficiency is an essential product attribute for marketing. Hence it was desirable to prepare AC with optimum yield, maximising the adsorption capacity. However, it was not always possible that the AC with highest yield would have the highest adsorption capacity. In order to compromise these two values, the desirability function was applied using the Design Expert software. The process condition that had the highest desirability was selected as the optimum condition. To identify this condition, the criterion was set as “in range” for the independent variables such as T, P, IR and concentration of acid. Criterion for the responses such as adsorption and yield were set as “maximise”. Based on the highest desirability value of 0.805, the optimum process condition obtained was 11.02 min of irradiation time, 676 W of microwave power, impregnation ratio of 0.68 and undiluted sulphuric acid. The predicted adsorption was 13.73 mg g⁻¹ and predicted yield was 77.73%. Validation experiments were conducted to confirm the values predicted from the model. In the validation experiment, it was found that the AC prepared in the optimum condition had adsorption capacity 14.6 mg g⁻¹ and yield of AC was 72%. The error in prediction was 6.41% and 7.1%, respectively. Table 4 enlists some results obtained in recent studies for adsorption of zinc.

Table 4 Comparative study for recent work for zinc adsorption

Adsorbent	Zinc adsorption capacity (mg g^−1)	Reference
Physic seed hull (PSH), Jantropha curcas L	12.29	35
Eichhornia crassipes biomass	12.55	36
Activated carbon prepared from Van apple pulp	11.72	37
Activated carbon prepared from Phaseolus aureus hulls	21.2	38
Activated carbon from Hevea brasiliensis	22.03	39
Activated carbon from Ceiba pentandra hulls	24.1	40

---

3.5. Characterisation of the AC

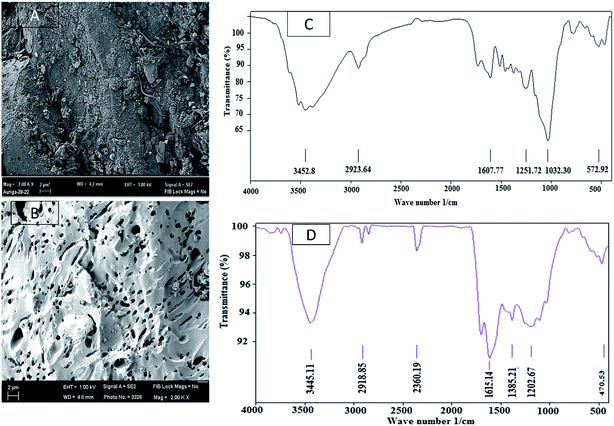
The AC was characterised by SEM, BET surface area and FTIR spectroscopy. The SEM image showed in Fig. 5(A) shows that the raw material had much less surface roughness and porosity on the surface. AC prepared in the optimum operating condition developed considerable amount of porosity after activation as evident from Fig. 5(B). The acid in the impregnation stage and microwave heating in the activation stage facilitated the formation of pores.

Fig. 5 SEM image (A and B) and FTIR spectra (C and D) of raw palm kernel shell AC, respectively.

FTIR data analysis showed that the intensity of the peak between 3500–3200 cm⁻¹, which was attributed to O–H stretching of alcohols or phenols, decreased to a great extent. Intensity of the band of 3000–2850 cm⁻¹ corresponding to C–H stretch of alkanes diminished in the AC. Both of these phenomena indicated that the sulphuric acid acted as dehydrating agent and had removed a considerable amount of hydrogen from the raw material⁴¹ to convert it to AC. The complex peaks around 1580–1650 cm⁻¹ in raw palm shell that could be attributed to N–H bend of primary amines and C–C stretch of aromatic ring. The intensity of this band had also reduced. The C–O stretch for alcohols, carboxylic acids, esters, ethers corresponding to the band 1300–1000 cm⁻¹ remained in the AC as in the raw material with a much lower intensity of the peak. This also suggested removal of hydrogen and oxygen part from the raw material.

Nitrogen adsorption/desorption isotherms determined the specific surface area through the utilisation of BET equation and was found to be 1011 m² g⁻¹. The pore size distribution curves showed that the AC contained mainly micro and meso pores which assisted in the adsorption process. The average pore diameter of the AC prepared at the optimum condition was 21.89 Å.

The adsorption/desorption isotherm of the AC prepared at the optimum condition in Fig. 6 shows that the curve is a “type I” isotherm, characterising micro-porous adsorbent for monolayer adsorption.⁴²

Fig. 6 Nitrogen adsorption/desorption isotherm for the AC prepared at the optimum condition showing type I isotherm.

4. Conclusion

The AC was prepared from PKS with sulphuric acid impregnation and by microwave heating. The heating time was only 11.02 min and this is considerably shorter than conventional production method. A statistical model was successfully adopted with the use of Design Expert software, which could predict the optimum condition efficiently. The suggested adsorption capacity and yield of AC was 13.73 mg g⁻¹ and 77.73%, respectively, at the optimum condition of 11.02 min of irradiation time, 676 W of microwave power, impregnation ratio of 0.68 and undiluted sulphuric acid. Experimental adsorption capacity of AC was found to be 14.6 mg g⁻¹ and yield was 72% with error in prediction of 6.41% and 7.1%, respectively. Characterisation study showed that the AC had highly porous surface and FTIR data confirmed dehydration and removal of hydrogen part from raw material to produce AC. BET surface area was found to be 1011 m² g⁻¹ which was considerably high.

Acknowledgements

The authors are grateful to University of Malaya (Project no. UM.C/HIR/MOHE/ENG/13 and IPPP University of Malaya, project no. PG040-2012B) for providing the fund for the research work.

References

1. H. Marsh and F. R. Reinoso, Activated carbon, Elsevier, 2006.
2. A. Bhatnagar, W. Hogland, M. Marques and M. Sillanpää, Chem. Eng. J., 2013, 219, 499–511.
3. E. Saputra, S. Muhammad, H. Sun and S. Wang, RSC Adv., 2013, 3, 21905–21910.
4. V. O. Njoku, K. Y. Foo, M. Asif and B. H. Hameed, Chem. Eng. J., 2014, 250, 198–204.
5. J. M. V. Nabais, C. E. C. Laginhas, P. J. M. Carrott and M. M. L. Ribeiro Carrott, Fuel Process. Technol., 2011, 92, 234–240.
6. R. Baccar, J. Bouzid, M. Feki and A. Montiel, J. Hazard. Mater., 2009, 162, 1522–1529.
7. M. U. Dural, L. Cavas, S. K. Papageorgiou and F. K. Katsaros, Chem. Eng. J., 2011, 168, 77–85.
8. G. San Miguel, G. D. Fowler and C. J. Sollars, Carbon, 2003, 41, 1009–1016.
9. T. Tay, S. Ucar and S. Karagöz, J. Hazard. Mater., 2009, 165, 481–485.
10. P.-T. Yeung, P.-Y. Chung, H.-C. Tsang, J. Cheuk-On Tang, G. Yin-Ming Cheng, R. Gambari, C.-H. Chui and K.-H. Lam, RSC Adv., 2014, 4, 38839–38847.
11. A. D. Russell, E. I. Antreou, S. S. Lam, C. Ludlow-Palafox and H. A. Chase, RSC Adv., 2012, 2, 6756–6760.
12. E. T. Thostenson and T. W. Chou, Composites, Part A, 1999, 30, 1055–1071.
13. M. A. Ahmad and R. Alrozi, Chem. Eng. J., 2010, 165, 883–890.
14. NIST/SEMATECH, in Process Improvement, ed. P. Tobias and L. Trutna, 2012, vol. 2013.
15. R. Verseput, Selecting the right central composite design for response surface methodology applications, 22 July 2014, http://www.qualitydigest.com/june01/html/doe.html.
16. M. Arulkumar, K. Thirumalai, P. Sathishkumar and T. Palvannan, Chem. Eng. J., 2012, 185–186, 178–186.
17. B. S. Kaith, R. Sharma, S. Kalia and M. S. Bhatti, RSC Adv., 2014, 4, 40339–40344.
18. R. J. E. Martins, R. Pardo and R. A. R. Boaventura, Water Res., 2004, 38, 693–699.
19. C. Lu, H. Chiu and C. Liu, Ind. Eng. Chem. Res., 2006, 45, 2850–2855.
20. V. K. Gupta and S. Sharma, Ind. Eng. Chem. Res., 2003, 42, 6619–6624.
21. F. Abnisa, W. M. A. Wan Daud and J. N. Sahu, Biomass Bioenergy, 2011, 35, 3604–3616.
22. F. Karacan, U. Ozden and S. Karacan, Appl. Therm. Eng., 2007, 27, 1212–1218.
23. E. Bayraktar, Process Biochem., 2001, 37, 169–175.
24. D. C. Montgomery, D. C. Montgomery and D. C. Montgomery, Design and analysis of experiments, Wiley, New York, 1984.
25. J. Acharya, J. N. Sahu, C. R. Mohanty and B. C. Meikap, Chem. Eng. J., 2009, 149, 249–262.
26. R. Sen and T. Swaminathan, Biochem. Eng. J., 2004, 21, 141–148.
27. H. Deng, G. Zhang, X. Xu, G. Tao and J. Dai, J. Hazard. Mater., 2010, 182, 217–224.
28. L.-Y. Hsu and H. Teng, Fuel Process. Technol., 2000, 64, 155–166.
29. M. Jagtoyen and F. Derbyshire, Carbon, 1998, 36, 1085–1097.
30. A.-N. A. El-Hendawy, A. J. Alexander, R. J. Andrews and G. Forrest, J. Anal. Appl. Pyrolysis, 2008, 82, 272–278.
31. R. Hoseinzadeh Hesas, A. Arami-Niya, W. M. A. Wan Daud and J. N. Sahu, Chem. Eng. Res. Des., 2013, 91(12), 2447–2456.
32. D. Xin-hui, C. Srinivasakannan, P. Jin-hui, Z. Li-bo and Z. Zheng-yong, Fuel Process. Technol., 2011, 92, 394–400.
33. K. Y. Foo and B. H. Hameed, Bioresour. Technol., 2012, 103, 398–404.
34. H.-y. Xia, J.-h. Peng, L.-b. Zhang, X.-y. MA, J.-h. TU and S.-m. Zhang, Chemical Engineering, 2007, 1, 012.
35. M. Mohammad, S. Maitra, N. Ahmad, A. Bustam, T. K. Sen and B. K. Dutta, J. Hazard. Mater., 2010, 179, 363–372.
36. C. Mahamadi and T. Nharingo, Bioresour. Technol., 2010, 101, 859–864.
37. T. Depci, A. R. Kul and Y. Önal, Chem. Eng. J., 2012, 200–202, 224–236.
38. M. M. Rao, D. K. Ramana, K. Seshaiah, M. C. Wang and S. W. C. Chien, J. Hazard. Mater., 2009, 166, 1006–1013.
39. H. Kalavathy, B. Karthik and L. R. Miranda, Colloids Surf., B, 2010, 78, 291–302.
40. M. M. Rao, G. P. C. Rao, K. Seshaiah, N. V. Choudary and M. C. Wang, Waste Manag., 2008, 28, 849–858.
41. R. H. Hesas, A. Arami-Niya, W. M. A. W. Daud and J. Sahu, BioResources, 2013, 8, 2950–2966.
42. O. Carmody, R. Frost, Y. Xi and S. Kokot, Surf. Sci., 2007, 601, 2066–2076.

---