Theoretical identification on the role of Lys15 for Sulfolobus tokodaii hexokinase

Abstract

Phosphorylation mechanisms of glucose catalyzed by complexes of glucose–ATP–Mg²⁺–StHK, glucose–ATP–Mg²⁺–K15A mutant and glucose–ATPγS–Mg²⁺–StHK have been extensively studied using the quantum mechanical/molecular mechanical (QM/MM) method. Structural analyses show that Mg²⁺ ion plays a key role in the stabilization of the β-phosphate in the whole catalytic reaction and contributes much to the departure of γ-phosphoryl (or γ-thiophosphoryl) group. Besides, the existence of K15 could also facilitate the stabilization of the β-phosphate directly and influence the binding of γ-phosphate (or γ-thiophosphate) with C6-hydroxyl group indirectly. For each complex, two catalytic processes (the phosphate transfer and proton transfer steps) are studied. The phosphate transfer process is calculated to be the rate-determining step in all three complexes, where the energy barrier of the phosphate transfer is 4.0, 11.7 and 10.9 kcal mol⁻¹ for glucose–ATP–Mg²⁺–StHK, glucose–ATP–Mg²⁺–K15A mutant and glucose–ATPγS–Mg²⁺–StHK complexes, respectively. Both the ATP and ATPγS bound StHK are exothermic, where the catalytic reaction is endothermic for K15A mutant. Calculations suggest that the influence of K15A mutation to the reactive activity is larger than that of the exchange of ATP to ATPγS. We suppose that K15 might play the similar role with those conserved arginine residue in human hexokinase I–IV.

---

1 Introduction

Phosphorylation of glucose to glucose 6-phosphate is important for both energy metabolism and biosynthesis in the cell. In eukaryotes, the enzyme that catalyzes the production of glucose 6-phosphate is catalyzed by hexokinases (EC 2.7.1.1), which can phosphorylate several hexoses, including mannose and fructose, in addition to glucose.¹ In bacteria, phosphorylation catalyzed by glucokinases (EC 2.7.1.2) is specific for glucose. Most Archaea use two types of glucokinase as follows: (i) ADP-dependent glucokinases,^2–7 or (ii) ATP-dependent glucokinases belonging to the repressors/open reading frames of unknown function/sugar kinases (ROK) family.^8,9 Various species of the hexokinase families have been studied, including human hexokinase,^10–14 rat and Schistosoma mansoni hexokinase,¹⁵ yeast hexokinase,^16–19 Escherichia coli glucokinase,²⁰ Arthrobacter sp. strain KM glucomannokinase,²¹ and Escherichia coli rhamnulose kinase.²²

Few studies have mentioned the hyperthermophilic archaeon Sulfolobus solfataricus.^23–25 Nishimasu et al. crystallized the ATP-dependent Sulfolobus tokodaii hexokinase (StHK)²⁶ structure for the first time. Kinetic analyses indicated that StHK was a novel hexokinase that could phosphorylate not only glucose but also glucosamine, mannose, and so on. So, StHK is distinct in its broad substrate specificity from other hexokinases. Nishimasu et al. also reported a crystal structure of the xylose–ADP–Mg²⁺–StHK tetrameric complex.²⁷ As no crystal structure bound to Mg²⁺ ion has been reported for the hexokinase family, this is the first report of the binding mode between StHK and Mg²⁺ in this family.

On the basis of experimental studies,^11,28 the catalytic base residue for human hexokinase I is D657, which functions as a proton acceptor to abstract the proton from the C6-hydroxyl group of glucose. This catalytic residue is structurally conserved in the hexokinase family. Besides, a conserved Arg residue (R539 for hexokinase I)^13,14 in the active site plays a key role in stabilizing the reaction intermediate using its positively charged side chain in human hexokinase I–IV, where it changes to K15 in StHK. This indicates that StHK would use a catalytic mechanism similar to those proposed for the other members of HK. However, an aspartate is not likely able to abstract the proton from the C6-hydroxyl group of glucose because the pK_a of an aspartate residue is low. It may be more likely that the phosphate transfer would proceed firstly through the metaphosphate-like transition state and an aspartate residue would accept the substrate proton at the later stage, as proposed for some other kinases.²⁹ A simplified theoretical model derived from the reported crystal structure of human pancreatic glucokinase (PDB ID: 3ID8)³⁰ was constructed using the two-layer ONIOM method incorporated in Gaussian 09,³¹ which only includes sugar (glucose and ribose), ATP, Mg²⁺, D205, and K169.³² The aim of their calculation is to understand the substituents effects of arsenic on phosphorylation. The goal of this work was to investigate the phosphorylation mechanism of StHK using the quantum mechanical/molecular mechanical (QM/MM) method. In order to investigate the importance of K15, the catalytic mechanism of K15A mutant was also studied. Moreover, a non-hydrolyzable ATP analog, ATPγS was used to replace ATP in order to further understand the catalytic mechanism of StHK.

2 Computational methods

2.1 Automated docking setup

The initial structure for this calculation was taken from a recently published crystal of StHK in complex with xylose, ADP, and Mg²⁺ (PDB ID: 2E2Q).²⁷ Since the crystal in complex with glucose and ATP had not been determined by experiment, the glucose and ATP were docked into the binding pocket using Autodock 4.0 program.³³ Before docking, substrates of glucose and ATP were optimized at the B3LYP/6-31G (d) level with Gaussian 03 package.³⁴ When docking, the grid scale was set as 60 Å × 60 Å × 60 Å based on grid module, with a spacing of 0.375 Å between grid points. Gasteiger charges³⁵ were set for both substrates and protein. 60 independent docking runs were performed. The protein was kept rigid, and all torsional bonds of the ligands were kept free. Based on a root-mean-square deviation criterion of 10 Å, docking results were clustered. Finally, the conformation with the more cluster member and the lowest protein–ligand interaction energy was chosen as the bioactive structure. The obtained docking tetrameric complex of glucose–ATP–Mg²⁺–StHK was overlapped with an adenosine 5-(β,γ-imino) triphosphate (AMP-PNP) containing glucokinase (glucose–(AMP-PNP)–Mg²⁺–glucokinase)³⁰ in order to check the reasonability of our mode. The whole superposition was shown in Fig. 1.

Fig. 1 Superposition of the docking conformation (gray) with the crystal structure of Mg²⁺-bound glucokinase in the presence of both glucose and AMP-PNP (PDB ID: 3ID8, cyan).

Based on the docking structure, the mutation of K15A was performed to obtain the tetrameric complex of glucose–ATP–Mg²⁺–K15A mutant, where one oxygen atom on the γ-phosphate group of ATP was replaced by a sulfur atom to obtain a non-hydrolyzable ATP analog (ATPγS) containing complex (glucose–ATPγS–Mg²⁺–StHK). For clarity, we use ATP-bound StHK, ATP-bound K15A mutant, and ATPγS-bound StHK to denote the tetrameric complex of glucose–ATP–Mg²⁺–StHK, glucose–ATP–Mg²⁺–K15A mutant, and glucose–ATPγS–Mg²⁺–StHK, respectively.

2.2 Computational model

The obtained docking structure, as well as the derived K15A mutant structure and ATPγS-bound complex were used as the initial structure of molecular dynamic (MD) simulation. The catalytic base residue D95 was modeled in deprotonated state. The protonation states and hydrogen atom positions of all other ionizable amino acid residues were altered based on PROPKA method.^36,37 Hydrogen atoms were added via the HBUILD facility in the CHARMM package.³⁸ Besides, the crystallographic water molecules found in the protein were retained at their original positions and the extra 6426 water molecules were added to form a 39 Å water sphere centered on D95. To neutralize each system, the number of adding Na⁺ ion is 3, 4 and 3 for the ATP-bound StHK, ATP-bound K15A mutant and ATPγS-bound StHK, respectively. To equilibrate the prepared system, several minimizations followed by a 1000 ps MD simulation were performed with the CHARMM22 forcefield.³⁹ During the subsequent QM/MM calculations, a total of 152,140,152 atoms in the active site were selected as the QM region for the ATP-bound StHK, ATP-bound K15A mutant and ATPγS-bound StHK, respectively, as shown in Fig. 2. The atomic coordinates of these atoms (QM part) are listed in ESI.† The remaining enzyme and waters were set as MM region. In the geometry optimizations, the QM region was treated with quantum mechanics by Turbomole module⁴⁰ and the MM part with molecular mechanics under the CHARMM22 forcefield by DL-POLY program.⁴¹ The whole calculations were carried out at B3LYP/6-31G(d)/CHARMM22 level. The charge shift model with hydrogen link atoms was adopted to simulate bonds and satisfy the valencies of covalently bonded atoms across the QM/MM boundary.⁴² Programs of ChemShell,⁴³ Turbomole and DL-POLY were combined to perform the QM/MM calculations. Geometry optimization was carried out by hybrid delocalized internal coordinates (HDLC) optimizer.⁴⁴ During the optimizations, stationary points were searched by the quasi-Newton limited memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm,^45,46 which was suitable for optimization problems with a large number of variables. Transition states were searched by the algorithm of partitioned rational function optimization (P-RFO).^47,48

Fig. 2 The selected QM and MM regions in the active site: (a) for ATP-bound StHK and ATP-bound K15A mutant; (b) for ATPγS-bound StHK.

3 Results and discussion

3.1 Docking structure

A global overlap of the docking conformation (gray) with a crystal structure of the Mg²⁺-bound glucokinase in the presence of both glucose and AMP-PNP (PDB ID: 3ID8, cyan) is given in Fig. 1. Residues D95 (catalytic base residue) and T116 in HK superpose well with D205 and T228 in glucokinase, respectively. The docked glucose and ATP overlap well with that of ligands glucose–(AMP-PNP)–Mg²⁺-bound crystal glucokinase. All these Asp residues of D71, D95 and D140 can form hydrogen bonds (HBs) with docked ligand glucose. Residue K15 has an electrostatic interaction with the oxygen atom on the β-phosphoryl group of ATP, where Mg²⁺ interact with both β- and γ-phosphoryl groups of ATP. It is shown that Mg²⁺ ion adopts an octahedral coordination, as was observed in the native structure.³⁰ All these descriptions indicate that the docking structure is reliable for the following QM/MM calculations.

In our study, the potential catalytic base residue is D95. However, since the pK_a of aspartate is low,²⁹ the aspartate itself can not be able to abstract the proton from C6-hydroxyl group of glucose. The most possible way is that the phosphate transfer would proceed before the proton transfer process from the substrate to D95.²⁹ In order to identify the role of K15, the catalytic mechanisms of wide type StHK and its K15A mutant were explored based on ATP as the phosphate donor. To further understand the catalytic mechanism of StHK, the non-hydrolyzable ATPγS was also used as the phosphate donor based on the wide type StHK. These mechanisms were studied separately in the following sections.

3.2 Catalytic mechanisms investigations

3.2.1 Catalytic mechanism investigation of ATP bound StHK. The final solvated model of prepared StHK after QM/MM optimization is displayed in Fig. 3a, and the active site of the optimized reactant (R1) is shown in Fig. 3b. For clarity, only the important residues surrounding the active site are listed. In this structure, the catalytic base residue D95 forms a strong HB (distance of 1.98 Å) with the C6-hydroxyl group of glucose. Other two Asp residues (D71 and D140) also form strong HBs with glucose. In fact, the two Asp residues always form strong HB interactions with glucose in the following phosphate transfer and proton transfer process, even in the ATP-bound K15A mutant, and ATPγS-bound StHK, which might contribute to the stability of glucose. Besides, the side chain of K15 forms a strong salt bridge interaction with the β-phosphate of ATP with a distance of 2.11 Å. The positively charged K15 contributes considerably to the cleavage of the P^γ–O^γ bond (labels are shown in Fig. 2). As an octahedral ion, Mg²⁺ coordinates with two phosphoryl oxygen atoms of ATP (distances of 2.07 Å and 2.10 Å) except with other four water molecules (Water 1–4). It assumes that these electrostatic interactions play a vital role in the following reactions. Similar to the function of positive K15, the strong electrostatic interactions formed between Mg²⁺ and phosphoryl oxygen atoms make the P^γ–O^γ bond be more weak, which might be favorable for the departure of the phosphoryl group.

Fig. 3 (a) The solvated model of prepared StHK for QM/MM calculation; (b) the active site of the optimized reactant (R1).

Structures of transition state (TS1 and TS2), intermediate (Int1), and product (P1) were searched using B3LYP/6-31G(d,p)//CHARMM22 geometrical optimization in an adiabatic mapping procedure.⁴⁹ The saddle and stationary points for the phosphory transfer were optimized to be TS1 and Int1 (as shown in Fig. 4), where saddle and stationary points for the proton transfer process were optimized to be TS2 and P1 (Fig. 5), respectively.

Fig. 4 Optimized structures in the phosphate transfer process of ATP-bound StHK: (a) for transition state (TS1); (b) for intermediate (Int1).

Fig. 5 Optimized structures in the proton transfer process of ATP-bound StHK: (a) for transition state (TS2); (b) for product (P1).

In TS1 (Fig. 4a), the linking P^γ–O^γ bond has changed from 1.77 Å in R1 to 2.29 Å. The γ-phosphorus atom has approached to the phosphate acceptor (C6-hydroxyl group of glucose) with a distance of 2.43 Å. Obviously, the γ-phosphate of ATP has partially transferred to the C6-hydroxyl group. During the γ-phosphate transfer process, the C6-hydroxyl group has strengthened its HB interaction with the catalytic base residue D95 (distance of which decreases to 1.85 Å). In this structure, the salt bridge formed between K15 and β-phosphate of ATP decreases to 1.94 Å, indicating that the established electrostatic interaction has been strengthened at this stage. The strengthened electrostatic interaction has two important roles: firstly, it contributes considerably to the cleavage of P^γ–O^γ bond; second, it is favorable for the stability of the departure part of ATP. The Mg–O (γ-phosphate) interaction distance is also longer in TS1 (2.13 Å) as compared to its reactant R1 (2.07 Å).

In Int1 (Fig. 4b), the older covalent P^γ–O^γ bond has elongated to 3.05 Å. The longer P^γ–O^γ bond distance reveals that the cleavage of the linking P^γ–O^γ bond has completed. The γ-phosphate of ATP has attached to the C6-hydroxyl group with the formation of a new covalent O6–P^γ bond (distance of 1.95 Å). With the departure of the leaving γ-phosphoryl group, ATP has changes to ADP. As the approach of the γ-phosphate to the phosphate acceptor, the ligand glucose has strengthened its HB interaction with D95 (distance of which decreases to 1.64 Å). The shorter distance indicates that the following proton transfer process is ready to occur. Though the γ-phosphate has moved to interact with the ligand glucose at this stage, the γ-phosphate still coordinates with Mg²⁺ ion (distance of 2.12 Å). Since Mg²⁺ could disperse its positive charge to γ-phosphate, this electrostatic interaction could stabilize the binding of γ-phosphate to C6-hydroxyl group. Furthermore, Mg²⁺ ion could also stabilize the leaving departure (ADP) because it still coordinates with β-phosphate of ADP. Besides, residue K15 also forms a sat bridge interaction with β-phosphate with a distance of 1.84 Å. It is shorter than that of the TS1, meaning the electrostatic interaction has been strengthened at this stage. The strengthened interaction is favorable for the stability of the leaving ADP.

The next step is the proton transfer process. When the catalytic base residue is D95, the proton abstract process corresponds one transition state (TS2) and product structure (P1), where the structures are shown in Fig. 5.

In the structure of TS2 (Fig. 5a), the proton of C6-hydroxyl group is abstracted by D95 and moves to a distance of 1.23 Å away from the carboxyl oxygen of D95, where the H–O bond of C6-hydroxyl is elongated to 1.24 Å. Besides, followed by the departure of the proton, the newly formed O6–P^γ bond decreases to 1.83 Å, indicating that this bond is strengthened during the proton transfer process. Though the O6–P^γ bond is further strengthened, the γ-phosphoryl group still coordinates with Mg²⁺ ion (distance of 2.10 Å). The charged Mg²⁺ makes the γ-phosphoryl group be more positive, which is favorable for the nucleophilic attack on the oxygen atom of C6-hydroxyl group. Similar to above structures, the residue K15 still coordinates with the β-phosphate of ATP and the salt bridge distance decreases to 1.82 Å, revealing that the salt bridge interaction is further strengthened.

In P1 (Fig. 5b), the H–O bond of C6-hydroxyl group increases to 1.68 Å, showing that the cleavage of this bond has completed. Obviously, D95 has abstracted the proton from glucose forming a new covalent H–O bond (1.02 Å). At this stage, the substrate of glucose has been phosphorylaed to glucose 6-phosphate. Though both phosphorylation and proton transfer processes has completed at this stage, the Mg²⁺ ion still coordinates with the β-,γ-phosphate tightly. For one thing, the electrostatic interaction formed between γ-phosphate and Mg²⁺ ion is favorable for the formation of glucose 6-phosphate, which might drive the proton transfer process. For another thing, the binding mode of Mg²⁺ with β-phosphate is also favorable for the stability of leaving ADP. Also, residue K15 further strengthens its interaction with β-phosphate of ADP with a distance of 1.80 Å, which is favorable for the stabilization the ADP.

3.2.2 Catalytic mechanism investigation of the ATP bound K15A mutant. The catalytic mechanism catalyzed by K15A mutant is explored at the same level. The optimized structures for the phosphorylation of glucose are shown in Fig. 6 and 7. For clarity, only important residues surrounding the active site are listed.

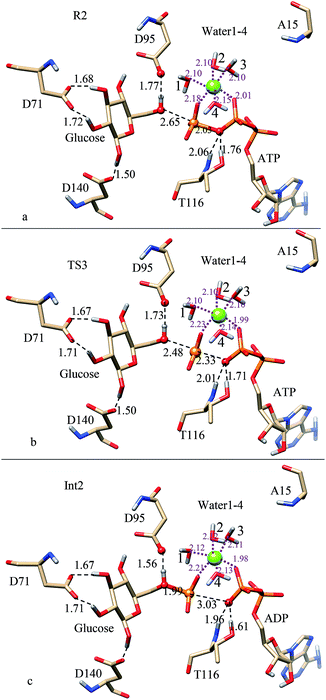Fig. 6 Optimized structures in the phosphate transfer process of ATP-bound K15A mutant: (a) for reactant (R2); (b) for transition state (TS3); (c) for intermediate (Int2).

Fig. 7 Optimized structures in the proton transfer process of ATP-bound K15A mutant: (a) for transition state (TS4); (b) for product (P2).

Fig. 6 gives the optimized reactant (R2), transition state (TS3), and intermediate (Int2) for the phosphate transfer process. Fig. 6a (R2) shows that the phosphoryl group of ATP adjusts to get closer to T116 when the electrostatic interaction formed between β-phosphate and K15 disappears. It can be seen that two HBs are formed (lengths of 1.76 and 2.06 Å) between them, meaning that the interaction between O^γ atom of ATP and T116 is strengthened. Though lacking contributions of positive charge supplied by K15, ATP could still coordinate with Mg²⁺ using its β-phosphate and γ-phosphate (distances of 2.01 and 2.18 Å, respectively). Besides, D95 forms a strong HB with the C6-hydroxyl group (distance of 1.77 Å). In this structure, P^γ atom of γ-phosphate is 2.65 Å away from the O6 atom of C6-hydroxyl group, which is 0.46 Å shorter than that of R1. The distance change may be due to the mutation of K15A, which results in the loss of electrostatic interaction formed between K15 and β-phosphate.

For TS3 (Fig. 6b), the length of P^γ–O^γ bond increases to 2.33 Å, where the distance between the O6 atom of C6-hydroxyl group and P^γ atom of γ-phosphate decreases to 2.48 Å. Obviously, the previous covalent P^γ–O^γ bond has broken at this stage, but the γ-phosphate has not been transferred to C6-hydroxyl group completely. As the breaking of P^γ–O^γ bond, the interaction formed between γ-phosphate and Mg²⁺ ion becomes weak (distance of 2.23 Å), where the β-phosphate strengthens its interaction with Mg²⁺ ion (distance of 1.99 Å). Besides, interactions formed between T116 and O^γ atom of ATP are also strengthened (1.71 and 2.01 Å). As the approach of the γ-phosphate, the C6-hydroxyl group strengthens its interaction with D95 (distance of 1.73 Å).

For Int2 (Fig. 6c), the P^γ–O^γ bond increases to 3.03 Å, where the distance between the O6 atom of C6-hydroxyl group and P^γ atom of γ-phosphate decreases 1.99 Å. So, the breaking of the P^γ–O^γ bond has completed at this stage, where ATP has changed to ADP. After the departure of the γ-phosphate, the β-phosphate strengthens its interactions with T116 and Mg²⁺ ion. It can be seen that HB distances between T116 and O^γ atom of ATP decrease to 1.61 and 1.96 Å, respectively. The strong HB interactions indicate that T116 might play an important role in the stability of the leaving ADP. As the approach of the γ-phosphate, the C6-hydroxyl group further strengthens its interaction with D95 (distance of 1.73 Å).

The optimized structures of transition state (TS4) and product (P2) for the proton transfer process are given in Fig. 7. In TS4 (Fig. 7a), the H–O bond length of C6-hydroxyl group increases to 1.19 Å, where the proton is abstracted by D95 to a distance of 1.24 Å. At the same time, the γ-phosphate group gets closer to O6 atom of C6-hydroxyl group followed by the departure of the proton (distance of 1.89 Å). Though the O6–P^γ bond is further strengthened, the γ-phosphoryl group still coordinates with Mg²⁺ ion with a distance of 2.17 Å. The charged Mg²⁺ might make the γ-phosphoryl group be more positive, which further facilitates the nucleophilic attack on O6 atom of C6-hydroxyl group.

In P2 (Fig. 7b), the H–O bond distance on C6-hydroxyl group increases to 1.75 Å, where the proton is only 1.00 Å away from the carboxyl oxygen atom of D95. Obviously, the proton abstraction process has completed at this stage, where the glucose has changed to glucose 6-phosphate. Similar to the wide type product P1, Mg²⁺ ion still coordinates with the β- and γ-phosphate tightly after the phosphorylation and proton transfer processes. Distance between Mg²⁺ and β-phosphate is shorter (1.96 Å) as compared to wide type product P1, where distance between Mg²⁺ and γ-phosphate is longer (2.13 Å). The length changes may be due to the mutation of K15. The positive charge of K15 may repulse Mg²⁺ to interact with β-phosphate, where in K15A mutant no such electric force exists.

3.2.3 Catalytic mechanism investigation of ATPγS bound StHK. To better understand the catalytic mechanism of StHK, the non-hydrolyzable ATP analog, ATPγS, was used to replace ATP. The catalytic mechanism of glucose–ATPγS–StHK complex is explored at the same level. Optimized structures of reactant (R3), transition state (TS5 and TS6), intermediate (Int3), and product (P3) for the phosphorylation and proton transfer processes are shown in Fig. 8 and 9, respectively.

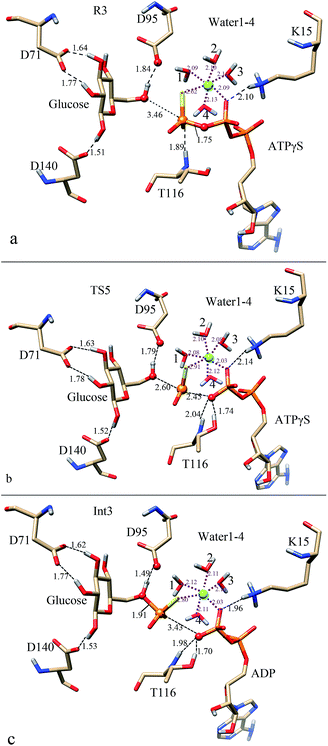Fig. 8 Optimized structures in the thiophosphate transfer process of ATPγS-bound StHK: (a) for reactant (R3); (b) for transition state (TS5); (c) for intermediate (Int3) structures.

Fig. 9 Optimized structures in the proton transfer process of ATPγS-bound StHK: (a) for transition state (TS6); (b) for product (P3).

The optimized structure R3 is shown in Fig. 8a. The distance between C6-hydroxyl group and D95 is 1.84 Å, and length between C6-hydroxyl group and γ-thiophosphoryl group of ATPγS is 3.46 Å. Since the γ-phosphate is replaced by γ-thiophosphoryl group here, Mg²⁺ ion weakens its interaction with γ-thiophosphoryl group (distance of 2.62 Å) and strengthens its interaction with β-phosphoryl group (distance of 2.09 Å) as comparing with R1. The weak electrostatic interactions formed between Mg²⁺ and phosphoryl group might facilitate the departure of the phosphoryl group. The positively charged K15 forms a strong salt bridge interaction with β-phosphate with a distance of 2.10 Å, which might contribute considerably to the cleavage of the P^γ–O^γ bond.

In TS5 (Fig. 8b), the linking P^γ–O^γ bond has changed from 1.75 Å in R3 to 2.45 Å. The γ-thiophosphorus atom has approached to the phosphate acceptor with a distance of 2.60 Å. Obviously, the γ-thiophosphoryl group has partially transferred to the C6-hydroxyl group. Comparing with TS1, the distance between γ-thiophosphate (γ-phosphate in TS1) and Mg²⁺ has elongated (2.91 Å vs. 2.13 in TS1). Besides, the S(γ-thiophosphate)–Mg interaction distance is also longer in TS5 as compared to its reactant R3 (2.62 Å). The increase of the S(γ-thiophosphate)–Mg interaction distance might reduce the positive charge distributions on the P^γ–O^γ bond, which is not favored for the breaking of P^γ–O^γ bond. Since the positively charged K15 still interacts with the β-phosphate with a distance of 2.14 Å, the breaking of the P^γ–O^γ bond might not be so difficult. As the approach of γ-thiophosphate to the phosphate acceptor, the C6-hydroxyl group has strengthened the HB interaction with D95 (distance of which decreases to 1.79 Å).

In Int3 (Fig. 8c), the older covalent P^γ–O^γ bond has elongated to 3.43 Å, and γ-thiophosphate is transferred to a distance of 1.91 Å away from the C6-hydroxyl group. These distance changes mean that the cleavage of the linking P^γ–O^γ bond has completed, where the ATP becomes ADP. As the approach of the γ-thiophosphate to the phosphate acceptor, the C6-hydroxyl group of glucose strengthens its HB interaction with D95 (distance of which decreases to 1.49 Å). Obviously, the proton of C6-hydroxyl group comes to a proper position, which is feasible following proton transfer process. Though phosphorylation of glucose takes place at this stage, the γ-thiophosphate still coordinates with Mg²⁺ ion (distance of 2.80 Å). But this distance is 0.68 Å longer than that in Int1. Since the charge of Mg²⁺ could be dispersed to γ-thiophosphate, the electrostatic interaction formed between γ-thiophosphate and Mg²⁺ ion is favorable for the binding of γ-thiophosphate to C6-hydroxyl group. Furthermore, Mg²⁺ ion could stabilize the leaving departure ADP because it coordinates with β-phosphate with a length of 2.03 Å. Besides, K15 also forms a sat bridge interaction with β-phosphate with a distance of 1.96 Å. It is shorter than that of the TS1, meaning the electrostatic interaction has been strengthened at this stage. The strengthened interaction is favorable for the stability of the leaving ADP.

Optimized structures of transition state (TS6) and product structure (P3) for the proton transfer step are shown in Fig. 9. In the structure of TS6 (Fig. 9a), the proton of C6-hydroxyl group moves to a distance of 1.29 Å from the carboxyl oxygen of D95, where the H–O bond of C6-hydroxyl elongates to 1.16 Å. Besides, followed by the departure of the proton, the newly formed O6–P^γ bond decreases to 1.86 Å, indicating that this bond is strengthened during the proton transfer process. Though the O6–P^γ bond is further strengthened, γ-thiophosphate still coordinates with Mg²⁺ ion with a distance of 2.78 Å. The charged Mg²⁺ makes the γ-thiophosphoryl group be more positive, which is favorable for the nucleophilic attack on O6 atom of C6-hydroxyl group. Similar to above structures, K15 still coordinates with the β-phosphate and the salt bridge distance decreases to 1.95 Å, indicating that the salt bridge interaction is further strengthened.

The final product (P3) is given in Fig. 9b. It shows that the H–O bond distance for C6-hydroxyl group increases to 1.81 Å, indicating that the cleavage of this bond has completed. Obviously, D95 has abstracted the proton from glucose with the formation of a covalent H–O bond (1.00 Å). Similar to P1, the γ-thiophosphate still coordinates with Mg²⁺ ion (distance of 2.75 Å). But this distance is 0.63 Å longer than that in P1, meaning that the electrostatic interaction formed between γ-thiophosphate and C6-hydroxyl group is relatively weak here. So, Mg²⁺ ion has less contribution to the binding of γ-thiophosphate in P3. However, the electrostatic interaction established between Mg²⁺ ion and β-phosphate is still very strong with a length of 2.03 Å. Besides, K15 also forms a sat bridge interaction with β-phosphate with a distance of 1.96 Å. Obviously, β-phosphate could be stabilized by positively charged Mg²⁺ and side chain of K15.

3.3 Analyses of the reaction energies for the catalytic mechanisms

After identifying the geometries of reactants, transition states, intermediates, and products, relative energies of these optimized structures are listed in ESI (Fig. S1†). More accurate energies are obtained by performing single point calculations at 6-31++G(2d,2p) basis set, as shown in Fig. 10. Since variation tendencies of the two figures are similar, only the more accurate energies shown in Fig. 10 are discussed below. In this figure, the energy barriers of ATP-bound StHK are shown in black line. The energy barrier of the γ-phosphate transfer process is calculated to be only 4.0 kcal mol⁻¹ (TS1). The relative energy of intermediate Int1 is −0.7 kcal mol⁻¹, indicating that the step of γ-phosphate transfer is a little exothermic. When D95 abstracts a proton from the C6-hydroxyl group, the energy barrier is calculated to be 3.5 kcal mol⁻¹. Comparing the two energy barriers with each other, we suppose that the γ-phosphate transfer process might be the rate-determining step. The relative energy of product (P1) is −0.9 kcal mol⁻¹, indicating that the final step is exothermic.

Fig. 10 The obtained relative energies in the phosphate transfer process and the proton transfer process. The curve colored in black, red and blue denotes the relative energies in ATP-bound StHK, ATP-bound K15A mutant, and ATPγS-bound StHK complexes, respectively.

The relative energies of ATP-bound K15A mutant are shown in red line. In general, mutation of K15 to A15 increases the energy barriers. It shows that the γ-thiophosphate transfer experiences a 11.7 kcal mol⁻¹ energy barrier to the intermediate Int2, the energy of which is much larger as compared to the corresponding wild type complex (TS1). The higher energy barrier contributes much to the disappearance of electrostatic interaction. As the departure of γ-phosphate to glucose, Mg²⁺ ion could interact easily with the β-phosphate without the repulse from positive K15. At the same time, it weakens its interaction with the γ-phosphoryl group. So, the energy barrier of the γ-phosphate transfer process becomes large. Here, the relative energy of intermediate Int2 is 11.6 kcal mol⁻¹ higher than that of the reactant, indicating that the γ-phosphate transfer step is endothermic. In the next proton transfer process, although the energy barrier is calculated to be 3.7 kcal mol⁻¹, the relative energy of TS4 (15.3 kcal mol⁻¹) is 3.6 kcal mol⁻¹ larger than that of TS3. Therefore, the proton transfer process might be the rate-determining step for the K15A mutant. The calculated energy of product P2 is 11.4 kcal mol⁻¹, showing that the final reaction is endothermic.

The relative energies of ATPγS-bound StHK are shown in blue line. It shows that the energy barrier of γ-thiophosphate transfer process is 10.9 kcal mol⁻¹ (TS5), which is similar to that of the K15A mutated complex. Though it is smaller than that of TS3, this energy is still much larger than that of TS1. Besides, the relative energy of intermediate Int3 is also larger as compared to the corresponding wild type complex (Int1). In the next proton transfer process, the energy barrier is calculated to be only 0.6 kcal mol⁻¹ and the relative energy of product P2 is only −0.1 kcal mol⁻¹. The γ-thiophosphate transfer process might also be the rate-determining step for this ATPγS-bound StHK.

Analyses of the energy profiles for three complexes of ATP-bound StHK, ATP-bound K15A mutant as well as ATPγS-bound StHK reveal that K15 plays a key role in StHK catalytic process. For one thing, the existence of K15 facilitates Mg²⁺ ion to interact with γ-phosphate (γ-thiophosphate), which facilitates indirectly the binding of γ-thiophosphate (γ-phosphate) with C6-hydroxyl group. For another thing, K15 can interact directly with β-phosphoryl group, which facilitates the cleavage of O6–P^γ bond. So, the influence of K15A mutation to the activity is larger than that of the exchange of ATP to ATPγS. We suppose that the residue K15 might play a similar role with the arginine residue in human hexokinase I–IV.

4 Conclusions

Phosphorylation mechanisms of glucose to glucose 6-phosphate in complexes of ATP-bound StHK, ATP-bound K15A mutant as well as ATPγS-bound StHK have been extensively studied using QM/MM approach. Structural analyses indicate that the existence of Mg²⁺ ion and K15 is favorable for the phosphorylation reaction to proceed. The Mg²⁺ ion always coordinates with β- and γ-phosphate (or γ-thiophosphate) in the whole catalytic reaction, and the binding mode can be changed when K15 mutates to A15. For one thing, the existence of K15 facilitates Mg²⁺ ion to interact with γ-phosphate (or γ-thiophosphate), which facilitates indirectly the binding of γ-phosphate (or γ-thiophosphate) with C6-hydroxyl group. For another thing, K15 can interact directly with β-phosphoryl group. Energy analyses reveal that the phosphate transfer step proceeds firstly followed by the proton transfer step, where the phosphate transfer step is always the rate-determining step in all three complexes. The energy barriers of the phosphate transfer steps are 4.0, 11.7 and 10.9 kcal mol⁻¹ for ATP-bound StHK, ATP-bound K15A mutant and ATPγS-bound StHK, respectively, suggesting that the influence of K15A mutation to the activity is larger than that of the exchange of ATP to ATPγS. Without the influence of K15 to Mg²⁺, catalytic reaction changes from an exothermic reaction to an endothermic one. We suppose that the residue K15 might play the similar role with those conserved arginine residue in human hexokinase I–IV.

Conflict of interest

The authors declare no competing financial interest.

Abbreviations

HK	Hexokinase
StHK	Sulfolobus tokodaii hexokinase
QM/MM	Quantum mechanical/molecular mechanical
ATPγS	Adenosine 5′-O-(thiotriphosphate)
R	Reactant
TS	Transition state
Int	Intermediate
P	Product
AMP-PNP	Adenosine 5-(β,γ-imino) triphosphate

Acknowledgements

This work is supported by NSFC (20875055, 21277081, 21477067), the Natural Science Foundation of China Postdoctoral Sustentation (2013M531603), Postdoctoral Innovation Project Special Funds of Shandong Province (201303109), Research Award Fund for Outstanding Young Scientists of Shandong Province (BS2013SW037), a Project of Shandong Province Higher Educational Science and Technology Program(J13LD04), Science-Technology Foundation for Middle-Aged and Young Scientists of Shandong Province (BS2011SF026).

References

1. M. L. Cárdenas, A. Cornish-Bowden and T. Ureta, Evolution and regulatory role of the hexokinases, Biochim. Biophys. Acta, Mol. Cell Res., 1998, 1401, 242–264.
2. S. W. Kengen, J. E. Tuininga, F. A. de Bok, A. J. Stams and W. M. de Vos, Purification and characterization of a novel ADP-dependent glucokinase from the hyperthermophilic archaeon Pyrococcus furiosus, J. Biol. Chem., 1995, 270, 30453–30457.
3. S. Kengen, F. De Bok, N. Van Loo, C. Dijkema, A. Stams and W. De Vos, Evidence for the operation of a novel Embden-Meyerhof pathway that involves ADP-dependent kinases during sugar fermentation by Pyrococcus furiosus, J. Biol. Chem., 1994, 269, 17537–17541.
4. S. Koga, I. Yoshioka, H. Sakuraba, M. Takahashi, S. Sakasegawa, S. Shimizu and T. Ohshima, Biochemical characterization, cloning, and sequencing of ADP-dependent (AMP-forming) glucokinase from two hyperthermophilic archaea, Pyrococcus furiosus and Thermococcus litoralis, Biochem. J., 2000, 128, 1079–1085.
5. C. Verhees, D. Koot, T. Ettema, C. Dijkema, W. de Vos and J. vander Oost, Biochemical adaptations of two sugar kinases from the hyperthermophilic archaeon Pyrococcus furiosus, Biochem. J., 2002, 366, 121–127.
6. H. Sakuraba, I. Yoshioka, S. Koga, M. Takahashi, Y. Kitahama, T. Satomura, R. Kawakami and T. Ohshima, ADP-dependent Glucokinase/Phosphofructokinase, a Novel Bifunctional Enzyme from the Hyperthermophilic ArchaeonMethanococcus jannaschii, J. Biol. Chem., 2002, 277, 12495–12498.
7. A. Labes and P. Schönheit, ADP-dependent glucokinase from the hyperthermophilic sulfate-reducing archaeon Archaeoglobus fulgidus strain 7324, Arch. Microbiol., 2003, 180, 69–75.
8. C. Dörr, M. Zaparty, B. Tjaden, H. Brinkmann and B. Siebers, The Hexokinase of the Hyperthermophile Thermoproteus tenax ATP-dependent hexokinases and ADP-dependent glucokinase, two alternatives for glucose phosphorylation in Archaea, J. Biol. Chem., 2003, 278, 18744–18753.
9. T. Hansen, B. Reichstein, R. Schmid and P. Schönheit, The first archaeal ATP-dependent glucokinase, from the hyperthermophilic crenarchaeon Aeropyrum pernix, represents a monomeric, extremely thermophilic ROK glucokinase with broad hexose specificity, J. Bacteriol., 2002, 184, 5955–5965.
10. K. Kamata, M. Mitsuya, T. Nishimura, J.-i. Eiki and Y. Nagata, Structural basis for allosteric regulation of the monomeric allosteric enzyme human glucokinase, Structure, 2004, 12, 429–438.
11. A. E. Aleshin, C. Kirby, X. Liu, G. P. Bourenkov, H. D. Bartunik, H. J. Fromm and R. B. Honzatko, Crystal structures of mutant monomeric hexokinase I reveal multiple ADP binding sites and conformational changes relevant to allosteric regulation, J. Mol. Biol., 2000, 296, 1001–1015.
12. C. Rosano, E. Sabini, M. Rizzi, D. Deriu, G. Murshudov, M. Bianchi, G. Serafini, M. Magnani and M. Bolognesi, Binding of non-catalytic ATP to human hexokinase I highlights the structural components for enzyme-membrane association control, Structure, 1999, 7, 1427–1437.
13. A. E. Aleshin, C. Zeng, G. P. Bourenkov, H. D. Bartunik, H. J. Fromm and R. B. Honzatko, The mechanism of regulation of hexokinase: new insights from the crystal structure of recombinant human brain hexokinase complexed with glucose and glucose-6-phosphate, Structure, 1998, 6, 39–50.
14. A. E. Aleshin, C. Zeng, H. D. Bartunik, H. J. Fromm and R. B. Honzatko, Regulation of hexokinase I: crystal structure of recombinant human brain hexokinase complexed with glucose and phosphate, J. Mol. Biol., 1998, 282, 345–357.
15. A. M. Mulichak, J. E. Wilson, K. Padmanabhan and R. M. Garavito, The structure of mammalian hexokinase-1, Nat. Struct. Mol. Biol., 1998, 5, 555–560.
16. W. S. Bennett Jr and T. A. Steitz, Structure of a complex between yeast hexokinase A and glucose: I. Structure determination and refinement at 3.5 Å resolution, J. Mol. Biol., 1980, 140, 183–209.
17. C. M. Anderson, R. E. Stenkamp and T. A. Steitz, Sequencing a protein by X-ray crystallography: II. Refinement of yeast hexokinase B Co-ordinates and sequence at 2.1 Å resolution, J. Mol. Biol., 1978, 123, 15–33.
18. T. A. Steitz, R. J. Flatterick, W. F. Anderson and C. M. Anderson, High resolution Xx-ray structure of yeast hexokinase, an allosteric protein exhibiting a non-symmetric arrangement of subunits, J. Mol. Biol., 1976, 104, 197–222.
19. P. R. Kuser, S. Krauchenco, O. A. Antunes and I. Polikarpov, The high resolution crystal structure of yeast hexokinase PII with the correct primary sequence provides new insights into its mechanism of action, J. Biol. Chem., 2000, 275, 20814–20821.
20. V. V. Lunin, Y. Li, J. D. Schrag, P. Iannuzzi, M. Cygler and A. Matte, Crystal structures of Escherichia coli ATP-dependent glucokinase and its complex with glucose, J. Bacteriol., 2004, 186, 6915–6927.
21. T. Mukai, S. Kawai, S. Mori, B. Mikami and K. Murata, Crystal Structure of Bacterial Inorganic Polyphosphate/ATP-glucomannokinase INSIGHTS INTO KINASE EVOLUTION, J. Biol. Chem., 2004, 279, 50591–50600.
22. D. Grueninger and G. E. Schulz, Structure and reaction mechanism of L-Rhamnulose kinase from Escherichia coli, J. Mol. Biol., 2006, 359, 787–797.
23. L. Chen, K. Brügger, M. Skovgaard, P. Redder, Q. She, E. Torarinsson, B. Greve, M. Awayez, A. Zibat and H.-P. Klenk, The genome of Sulfolobus acidocaldarius, a model organism of the Crenarchaeota, J. Bacteriol., 2005, 187, 4992–4999.
24. Q. She, R. K. Singh, F. Confalonieri, Y. Zivanovic, G. Allard, M. J. Awayez, C.-Y. Christina, I. G. Clausen, B. A. Curtis and A. De Moors, The complete genome of the crenarchaeon Sulfolobus solfataricus P2, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7835–7840.
25. Y. Kawarabayasi, Y. Hino, H. Horikawa, K. Jin-no, M. Takahashi, M. Sekine, S.-i. Baba, A. Ankai, H. Kosugi, A. Hosoyama, S. Fukui, Y. Nagai, K. Nishijima, R. Otsuka, H. Nakazawa, M. Takamiya, Y. Kato, T. Yoshizawa, T. Tanaka, Y. Kudoh, J. Yamazaki, N. Kushida, A. Oguchi, K. Aoki, S. Masuda, M. Yanagii, M. Nishimura, A. Yamagishi, T. Oshima and H. Kikuchi, Complete genome sequence of an aerobic thermoacidophilic crenarchaeon, Sulfolobus tokodaii strain7, DNA Res., 2001, 8, 123–140.
26. H. Nishimasu, S. Fushinobu, H. Shoun and T. Wakagi, Identification and characterization of an ATP-dependent hexokinase with broad substrate specificity from the hyperthermophilic archaeon Sulfolobus tokodaii, J. Bacteriol., 2006, 188, 2014–2019.
27. H. Nishimasu, S. Fushinobu, H. Shoun and T. Wakagi, Crystal structures of an ATP-dependent hexokinase with broad substrate specificity from the hyperthermophilic archaeon Sulfolobus tokodaii, J. Biol. Chem., 2007, 282, 9923–9931.
28. K. Arora, C. Filburn and P. Pedersen, Glucose phosphorylation. Site-directed mutations which impair the catalytic function of hexokinase, J. Biol. Chem., 1991, 266, 5359–5362.
29. M. Valiev, R. Kawai, J. A. Adams and J. H. Weare, The role of the putative catalytic base in the phosphoryl transfer reaction in a protein kinase: first-principles calculations, J. Am. Chem. Soc., 2003, 125, 9926–9927.
30. P. Petit, M. Antoine, G. Ferry, J. A. Boutin, A. Lagarde, L. Gluais, R. Vincentelli and L. Vuillard, The active conformation of human glucokinase is not altered by allosteric activators, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2011, 67, 929–935.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
32. A. Jissy and A. Datta, Can Arsenates Replace Phosphates in Natural Biochemical Processes? A Computational Study, J. Phys. Chem. B, 2013, 117, 8340–8346.
33. G. M. Morris, D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew and A. J. Olson, Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function, J. Comput. Chem., 1998, 19, 1639–1662.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C. 02, Gaussian, Inc., Wallingford, CT, 2004.
35. J. Gasteiger and M. Marsili, Iterative partial equalization of orbital electronegativity—a rapid access to atomic charges, Tetrahedron, 1980, 36, 3219–3228.
36. H. Li, A. D. Robertson and J. H. Jensen, Very fast empirical prediction and rationalization of protein pK_a values, Proteins, 2005, 61, 704–721.
37. D. C. Bas, D. M. Rogers and J. H. Jensen, Very fast prediction and rationalization of pK_a values for protein–ligand complexes, Proteins, 2008, 73, 765–783.
38. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, CHARMM: a program for macromolecular energy, minimization, and dynamics calculations, J. Comput. Chem., 1983, 4, 187–217.
39. A. D. MacKerell Jr, D. Bashford, M. Bellot, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. Reiher, W. E. B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins, J. Phys. Chem. B, 1998, 102, 3586–3616.
40. R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Electronic structure calculations on workstation computers: the program system TURBOMOLE, Chem. Phys. Lett., 1989, 162, 165–169.
41. W. Smith and T. R. Forester, DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package, J. Mol. Graphics Modell., 1996, 14, 136–141.
42. A. H. de Vries, P. Sherwood, S. J. Collins, A. M. Rigby, M. Rigutto and G. J. Kramer, Zeolite structure and reactivity by combined quantum-chemical-classical calculations, J. Phys. Chem. B, 1999, 103, 6133–6141.
43. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjovoll, A. Fahmi, A. Schafer and C. Lennartz, QUASI: A general purpose implementation of the QM/MM approach and its application to problems in catalysis, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28.
44. S. R. Billeter, A. J. Turner and W. Thiel, Linear scaling geometry optimisation and transition state search in hybrid delocalised internal coordinates, Phys. Chem. Chem. Phys., 2000, 2, 2177–2186.
45. J. Nocedal, Updating quasi-Newton matrices with limited storage, Math. Comput., 1980, 35, 773–782.
46. D. C. Liu and J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Program, 1989, 45, 503–528.
47. A. Banerjee, N. Adams, J. Simons and R. Shepard, Search for stationary points on surfaces, J. Phys. Chem., 1985, 89, 52–57.
48. J. Baker, An algorithm for the location of transition states, J. Comput. Chem., 1986, 7, 385–395.
49. H. L. Woodcock, M. Hodošček and B. R. Brooks, Exploring SCC-DFTB paths for mapping QM/MM reaction mechanisms, J. Phys. Chem. A, 2007, 111, 5720–5728.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra16652c

---