Separation of the molecular motion from different components or phases using projection moving-window 2D correlation FTIR spectroscopy for multiphase and multicomponent polymers
Tao Zhou*,
Ting Zhou and
Aiming Zhang
State Key Laboratory of Polymer Materials and Engineering of China, Polymer Research Institute, Sichuan University, Chengdu 610065, China. E-mail: zhoutaopoly@scu.edu.cn; Fax: +86-28-85402465; Tel: +86-28-85402601
First published on 26th January 2015
Abstract
This study developed a new analytical method called projection moving-window 2D correlation FTIR spectroscopy (Proj-MW2D) to separate the molecular motion of groups generated from different components or phases for multiphase and multicomponent polymers. The specific implementation steps for Proj-MW2D were enumerated after the theoretical derivation and algorithm research. Two types of two-component blends, poly(L-lactide)/poly(butylene succinate) and monodisperse polystyrene/monodisperse poly(ethylene-co-1-butene), were employed to validate the concept of separating the molecular motion of groups. Results showed that the Proj-MW2D FTIR correlation technique successfully separated the molecular motion of the specific functional groups. Although MW2D and PCMW2D have the capacity to determine the multiple transitions of polymers, they cannot identify the origin of correlation intensity peaks without the help of other characterization methods. Proj-MW2D allows researchers to study the mechanism of the complex transition process for multiphase and multicomponent polymer systems. This method can be easily extended to three- or four-component polymers and to other spectra (e.g., Raman, X-ray, and UV).
1. Introduction
Polymers have a complex transition behavior. Since the discovery of polymers in organic materials chemistry, scientists have successfully developed numerous techniques to characterize polymer transition behavior.1 The advancements in characterization methods have expanded our knowledge on polymer materials. Infrared (IR) spectroscopy is a classic method for polymers. It produced a vibrational spectrum that reflects the dipole vibrations of specific bonds in polymers.2,3 Therefore, IR spectroscopy provides molecular information at the functional group level.Generalized 2D correlation vibrational spectroscopy, which was inspired from 2D NMR, was proposed by Noda in 1993.4 This technique uses Fourier transform and convolution to apply correlation analysis for in situ IR with an external perturbation.5 Peoples can employ it to study the interaction mechanism of functional groups in detail during polymer transitions. Given its practicality, generalized 2D correlation spectroscopy has rapidly become a new popular method of characterization.6–11 However, 2D correlation spectroscopy cannot establish the relationship of correlation intensity peaks between spectral variables (e.g., wavenumber, Raman shift) and external perturbation variables (e.g., temperature, pressure). Thomas and Richardson12 proposed moving-window 2D correlation spectroscopy (MW2D) in 2000. The correlation intensity peaks of spectral variables directly associate with those of external perturbation variables in this technique; therefore, the transition points of polymers and the transition range can be precisely determined.13–19 Morita20 introduced perturbation-correlation moving-window 2D correlation spectroscopy (PCMW2D) in 2006. Summary findings of scientists over many years found that the combination of MW2D or PCMW2D, and generalized 2D correlation spectroscopy was the best way.17,18,21–26 In general, MW2D or PCMW2D is employed to determine the transition point and the transition range of polymers; then, generalized 2D spectroscopy is performed to study the mechanism of functional groups at a specific transition.17,18,21–26 Compared with generalized 2D spectroscopy, 2D correlation spectroscopy with moving-window (MW2D or PCMW2D) has inherent advantages on studying the multiple transitions of polymers.
Generalized 2D correlation IR spectra are sometimes complex in practical applications. Specifically, the overlapping of correlation peaks is serious or looks “crowded”. Explaining these spectra via Noda's rules is difficult because of the interference of correlation intensity peaks.4,5 This phenomenon is obvious in multiphase and multicomponent polymer systems. In some block copolymers (SBS, SIS, and SEPS) and polymer blends, the correlation intensity peaks of minor components tend to be masked when main components dominate the transitions. Therefore, caution must be implemented when using generalized 2D correlation FTIR spectroscopy to study multiphase and multicomponent polymer systems. Considering this problem, Noda27 proposed the projection technique for generalized 2D correlation spectroscopy in 2010. This method was extended from double 2D correlation analysis.28 The projection technique was specifically developed for complex systems. This technique simplifies the “crowded” 2D correlation spectra by distinguishing the corresponding correlation intensity from different components. The concept of projection has aroused great interest among scientists.29,30 However, generalized 2D correlation spectroscopy combined with projection still has some limitations on multiphase and multicomponent polymer systems because most polymers show multiple transitions under an external perturbation (e.g., temperature). Although MW2D or PCMW2D correlation spectroscopy has inherent capacity to determine the multiple transitions of polymers, it cannot identify the origin of correlation intensity peaks without the help of other characterization methods. To overcome these difficulties, this study developed a method called projection moving-window 2D correlation spectroscopy (Proj-MW2D) to separate the molecular motion of groups generated from different components in multicomponent polymers. The new approach not only has a capacity to precisely specify multiple transition points of polymers, but also can separate the molecular motion of groups. It will be particularly suitable to the study of the molecular movement mechanism of a specific transition for polymer systems.
In this paper, through theoretical derivation, algorithm research, and infrared spectroscopy experiments, the projection technique was successfully integrated into MW2D. Fig. 1 illustrates the proposed concept of separating the molecular motion of groups from different components. Proj-MW2D is a promising analytical method. This method possibly has potential outstanding and special applications in multiphase and multicomponent polymers.
 | ||
| Fig. 1 Schematic of the proposed concept of separating the molecular motion of groups from different components for multicomponent polymers. | ||
2. Method
2.1. Spectral data matrix
The theoretical derivation of the method is outlined below.Proj-MW2D needs to divide the entire spectral data matrix as a series of sub-matrices. Each sub-matrix is called as a window.
A is supposed to be an M × N matrix of spectral data with M rows and N columns. v and I represent the spectral variables (e.g., wavenumber) and external perturbation variables (e.g., temperature), respectively. Each row of A corresponds to the discrete data points of a spectrum.
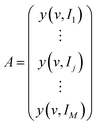 | (1) |
The sub-matrix Aj is extracted from the main matrix A. At this point, the serial number of the perturbation variable I ranges from j − m to j + m. Obviously, the sub-matrix Aj has 2m + 1 rows, whose column number is equal to the main matrix A. 2m + 1 is the window size.
The sub-matrix Aj can be expressed as
 | (2) |
In general, the reference spectrum and the dynamic spectrum of the jth sub-matrix are calculated by the following formulas.
 | (3) |
| ỹ(v, IJ) = y(v, IJ) − ȳ(v) | (4) |
The mean-centered jth sub-matrix can be described as follows.
 | (5) |
2.2. Projection matrix
A matrix Y has 2m + 1 rows and k columns, and the rows (2m + 1) of Y should be the same as those of Ãj. The matrix Y reduces to a single vector y when Y has only one column.The singular value decomposition (SVD) of matrix Y is defined as follows.
| Y = UYSYVTY + EY | (6) |
SVD is a common method of extracting important features from a mathematical concept.31 It can be applied to an arbitrary matrix. SVD is attributed to the important field of data mining. Many applications can be related to SVD. These applications include PCA with the feature extraction, the data compression algorithm (represented by the image compression), and the latent semantic indexing for search engine.
UY is a matrix of (2m + 1) × (2m + 1). VTY is a square matrix of k × k. SY is a (2m + 1) × k matrix, and its diagonal elements of σ1, σ2, …, σk are the singular values of the matrix Y. EY is the residual matrix. Generally, it is small enough to be negligible. Here, we give an index r, which makes the value of (σ1 + σ2 + … + σr)/(σ1 + σ2 + … + σr + … + σk) greater than or equal to 0.9 (90%), and the 1, …, (2m + 1) rows and the 1, …, r columns of UY are used for the subsequent calculations.
Then, the projection matrix RY from Y can be calculated as:
| RY = UYUTY | (7) |
RY is a (2m + 1) × (2m + 1) matrix. The used (2m + 1) × r part of UY avoids RY transform to an identity matrix. The corresponding null-space projection matrix is defined as:
| (I − RY) = I − UYUTY | (8) |
2.3. Generalized projection transformation
Ãj matrix can be transformed into a new matrix of ÃPj with the projection according to the following formula:| ÃPj = RYÃj | (9) |
The corresponding null-space projection matrix is:
| ÃNj = Ãj − ÃPj | (10) |
In the jth sub-matrix, the projection synchronous and projection asynchronous 2D correlation spectra can be calculated as:
| ΦPj = (ÃPj)TÃPj | (11) |
| ΨPj = (ÃPj)TNÃPj | (12) |
The corresponding null-space projection synchronous and null-space projection asynchronous 2D correlation spectra are calculated as:
| ΦNj = (ÃNj)TÃNj | (13) |
| ΨNj = (ÃNj)TNÃNj | (14) |
2.4. Positive projection transformation
According to Noda's proposal,27 the loading matrix L of ÃPj is defined as:| L = ÃTjUY | (15) |
Then, ÃPj can be expressed as:
| ÃPj = UYLT | (16) |
In this study, we introduce a positive loading matrix L+, which comes from L by data processing. L+ retains the elements of ≥0 in L, and the elements of <0 are replaced by 0. After positive projection transformation, we obtain a new projection matrix ÃP+j. ÃP+j only reserves the columns in ÃPj that have the same change (or orientation) direction as in matrix Y.
| ÃP+j = UYLT+ | (17) |
The corresponding null-space projection matrix is:
| ÃN+j = Ãj − ÃP+j | (18) |
Then, the projection synchronous and projection asynchronous 2D correlation spectra in the jth sub-matrix are calculated as follows:
| ΦP+j = (ÃP+j)TÃP+j | (19) |
| ΨP+j = (ÃP+j)TNÃP+j | (20) |
The corresponding null-space projection synchronous and null-space projection asynchronous 2D correlation spectra are calculated as follows:
| ΦN+j = (ÃN+j)TÃN+j | (21) |
| ΨN+j = (ÃN+j)TNÃN+j | (22) |
2.5. Moving-window
A series of sub-matrices are obtained by sliding the window position from j = 1 + m to j = M − m. The calculations are repeatedly performed using the above equations for each sub-matrix (window). Then, an overlay operation that is identical to the conventional MW2D algorithm is employed to gain a Proj-MW2D correlation spectrum13,17 and a null-space Proj-MW2D correlation spectrum. For convenient explanation and calculations, our study focuses on Proj-MW2D and null-space Proj-MW2D based on auto-correlation.2.6. Multiple projection for three to four components (or phases)
The algorithm mentioned above is only applicable to polymers with two components (or phases). The multiple projection operation should be introduced to investigate three- to four-component (phases) polymers.ÃNj or ÃN+j is specified as a new spectral data matrix. We select matrix Y1 as another projection to repeat eqn (6)–(10) or eqn (15)–(18). Then, the spectral data matrix ÃP1j or ÃP1+j with the second projection and the spectral data matrix ÃN1j or ÃN1+j with null-space second projection are obtained.
| ÃP1j = RY1ÃNj | (23) |
| ÃN1j = ÃNj − ÃP1j | (24) |
| ÃP1+j = UY1LT1+ | (25) |
| ÃN1+j = ÃN+j − ÃP1+j | (26) |
This algorithm allows Proj-MW2D to analyze polymer systems with three components (or phases). Similarly, using ÃP1j or ÃP1+j as a new spectral data matrix for the third projection, we can use Proj-MW2D to analyze polymer systems with four components (or phases).
2.7. Selection of the projection matrix Y
The projection matrix Y influences the final results. The matrix Y can be selected from the jth sub-matrix Ãj, which has the mean-centered processing. Generally, the matrix Y contains a few columns of Ãj. In the actual spectrum (e.g., IR), these columns contain some characteristic bands. It degenerates into a vector when Y has only one column of Ãj, which corresponds to a characteristic spectral peak. Selecting the projection matrix Y from the spectral data matrix Ãj can satisfy most of our needs. The projection matrix Y can also be chosen from other sources, such as from another experiment of IR or Raman spectra. External perturbations (such as temperature or concentration) can be also selected as the projection matrix Y. In some cases, specific mathematical functions can be used as a projection matrix for model-based analyses. In Proj-MW2D correlation spectroscopy, the construction method of the projection matrix Y is similar to Noda's proposal.2.8. Implementation steps for polymers
Polymer blends with two components (or phases), such as A + B, are used as an example to show the implementation steps of Proj-MW2D in separating the molecular motion of groups. The basic steps are outlined below:(1) In situ spectral data of polymer blend samples are collected in the presence of an external perturbation (temperature, concentration, etc.). Collecting the maximum number of spectra ensured by the signal–noise ratio and allowed by the spectrometer collection rate is recommended to accurately describe the physical or chemical processes of the samples.
(2) The projection matrix Y is constructed. In general, Y is selected from the interest characteristic bands in the in situ spectral data. For multiphase and multicomponent polymers, Y is often chosen from the most characteristic bands that can represent a phase or a component. This characteristic bands can distinguish the interest component from the other components (or phases). For two-component polymer blends, we choose certain characteristic bands of component A (denoted as a) to construct the projection matrix.
(3) Proj-MW2D correlation spectra are calculated using the positive projection transformation algorithm. The algorithm can be compiled into program using C and C++ computer language or using Matlab directly.
(4) Proj-MW2D correlation spectrum and null-space Proj-MW2D correlation spectrum are obtained. For two-component polymer blends, the response of correlation intensities from component A appear in Proj-MW2D correlation spectra, and the response of correlation intensity from component B presents in null-space Proj-MW2D correlation spectra. The reason for this result is that the response with the same variation feature as the characteristic bands (a) of component A is retained by the positive projection algorithm.
(5) The transition range of components A and B is determined according to the response of the correlation intensity. The individual physical and chemical transitions of A or B and collaborative transitions of A + B involved can be identified. Then, the mechanism and bands' assignment can be further analyzed.
3. Experimental section
In this study, two types of two-component polymer blends were prepared using different blending methods. The molecular motion of groups generated from different components was separated using Proj-MW2D correlation analysis.3.1. Materials
Poly(L-lactide) (4032D) was provided by NatureWorks LLC, USA. Poly(butylene succinate) (Bionolle 1001MD) was provided by Showa Highpolymer Co., Ltd, Japan. Monodisperse polystyrene (PS) and monodisperse poly(ethylene-co-1-butene) (EB, also known as fully hydrogenated polybutadiene) synthesized via anionic polymerization were supplied by Baling Petrochemical Industry Co., Ltd (Sinopec). Cyclohexane with 99.5% (AR) purity was produced by Chemical Reagent Union Co., Ltd. The weight average molecular weight of monodisperse PS was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, and its monodisperse coefficient was 1.04 (GPC). The weight average molecular weight of monodisperse EB was 120
000 g mol−1, and its monodisperse coefficient was 1.04 (GPC). The weight average molecular weight of monodisperse EB was 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, and its monodisperse coefficient was 1.05 (GPC). The molar content of 1-butene in EB was 29% (NMR). Poly(butylene succinate) (PBS), poly(L-lactide) (PLLA), monodisperse polystyrene (PS), and monodisperse poly(ethylene-co-1-butene) (EB) were directly used without further purification. The molecular structures of these materials are shown in Scheme 1.
000 g mol−1, and its monodisperse coefficient was 1.05 (GPC). The molar content of 1-butene in EB was 29% (NMR). Poly(butylene succinate) (PBS), poly(L-lactide) (PLLA), monodisperse polystyrene (PS), and monodisperse poly(ethylene-co-1-butene) (EB) were directly used without further purification. The molecular structures of these materials are shown in Scheme 1.
3.2. Preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. The temperature of melt blending ranged from 175 °C to 185 °C, and the screw speed was 180 rpm.
50. The temperature of melt blending ranged from 175 °C to 185 °C, and the screw speed was 180 rpm.3.3. Temperature-dependent FTIR spectroscopy
A Nicolet iS10 FTIR spectrometer equipped with a deuterated triglycine sulfate detector was used. The FTIR spectral resolution was 4 cm−1, and 20 scans were co-added for each FTIR spectrum.3.4. Proj-MW2D correlation analysis
Proj-MW2D correlation FTIR spectra were processed and calculated using 2DCS 6.1 software, developed by one of the authors using Visual C++. Before the analysis, the IR spectra were treated using a linear baseline correction. The window size was chosen as 2m + 1 = 11 to produce high-quality Proj-MW2D FTIR spectra and null-space Proj-MW2D FTIR spectra. The 1% correlation intensity of the Proj-MW2D and null-space Proj-MW2D correlation spectra was regarded as noise and was cut off. In the 2D spectra, red and blue areas represent positive and negative correlation intensities, respectively.4. Results and discussion
4.1. Separation of the molecular motion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O groups from the crystalline phase of the PBS component during PLLA/PBS crystallization upon cooling
O groups from the crystalline phase of the PBS component during PLLA/PBS crystallization upon cooling
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of PBS and PLLA.36–41 Some minor changes are observed within 1850 cm−1 to 1635 cm−1 when the temperature decreases from 120 °C to 50 °C. The peak intensity at 1759 cm−1 gradually increases, whereas the bands at 1714 cm−1 slightly move to the lower wavenumber. These results show that temperature-dependent FTIR cannot separate the molecular motion from the C
O stretching vibration of PBS and PLLA.36–41 Some minor changes are observed within 1850 cm−1 to 1635 cm−1 when the temperature decreases from 120 °C to 50 °C. The peak intensity at 1759 cm−1 gradually increases, whereas the bands at 1714 cm−1 slightly move to the lower wavenumber. These results show that temperature-dependent FTIR cannot separate the molecular motion from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in the PBS crystalline phase. Our target is to use Proj-MW2D to separate the C
O groups in the PBS crystalline phase. Our target is to use Proj-MW2D to separate the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O motion generated from the PBS crystalline phase during PLLA/PBS crystallization.
O motion generated from the PBS crystalline phase during PLLA/PBS crystallization.
| Wavenumber (cm−1) | Assignment | |
|---|---|---|
| PLLA | PBS | |
| 1759 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration O stretching vibration |
— |
| 1714 | — | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration O stretching vibration |
| 955 (960–930) | CH3 rocking + C–C stretching | C–O symmetric stretching |
| 919 (924–920) | 103 helical chain skeletal deformation | CH2 skeletal deformation |
| 806 | — | CH2 in-plane bending in OC(CH2)2CO |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| PS | EB | |
| 2925 | CH2 antisymmetric stretching vibration of the main chain | CH2 antisymmetric stretching vibration |
| 2856 | CH2 symmetric stretching vibration of the main chain | CH2 symmetric stretching vibration |
| 1462 | — | CH2 bending vibration |
| 1453 | CH2 bending vibration of the main chain | — |
| 757 | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH out-of-plane bending vibration of benzene rings CH out-of-plane bending vibration of benzene rings |
— |
| 720 | — | CH2 rocking of the ethylene units |
| 698 | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH out-of-plane bending vibration of benzene rings CH out-of-plane bending vibration of benzene rings |
— |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups from PBS crystalline phase, the projection matrix (or vector) should be the characteristic bands of PBS and the bands can accurately describe the functional group movements of the PBS crystalline phase during crystallization. In addition, the bands should not overlap with any bands of the PLLA component. In Fig. 2, also refer to the literature,38,42 we find three characteristic bands of PBS at 955, 919, and 806 cm−1. The bands at 955 cm−1 is assigned to the C–O symmetric stretching of PBS.42 The bands at 919 cm−1 is attributed to the CH2 skeletal deformation of PBS,38,42 and that at 806 cm−1 is attributed to the CH2 in-plane bending in OC(CH2)2CO.42 These three bands can be judged as the crystallization bands of PBS because their intensities gradually increase as the temperature decreases from 120 °C to 50 °C. The crystallization behavior of PBS in PLLA/PBS is clearly described by 955, 919, and 806 cm−1 upon cooling. However, according to the literature,43,44 the bands in 960 cm−1 to 930 cm−1 and 924 −1 to 920 cm−1 regions are also assigned to the CH3 rocking +C–C stretching and 103 helical chain skeletal deformation of the PLLA component, respectively. Therefore, in Fig. 2, only 806 cm−1 is fully attributed to PBS. The bands at 806 cm−1 does not overlap with any bands of PLLA, and it accurately describes the crystallization behavior of PBS. The molecular structure of PBS also shows that the corresponding CH2 groups of 806 cm−1 directly connect to the C
O groups from PBS crystalline phase, the projection matrix (or vector) should be the characteristic bands of PBS and the bands can accurately describe the functional group movements of the PBS crystalline phase during crystallization. In addition, the bands should not overlap with any bands of the PLLA component. In Fig. 2, also refer to the literature,38,42 we find three characteristic bands of PBS at 955, 919, and 806 cm−1. The bands at 955 cm−1 is assigned to the C–O symmetric stretching of PBS.42 The bands at 919 cm−1 is attributed to the CH2 skeletal deformation of PBS,38,42 and that at 806 cm−1 is attributed to the CH2 in-plane bending in OC(CH2)2CO.42 These three bands can be judged as the crystallization bands of PBS because their intensities gradually increase as the temperature decreases from 120 °C to 50 °C. The crystallization behavior of PBS in PLLA/PBS is clearly described by 955, 919, and 806 cm−1 upon cooling. However, according to the literature,43,44 the bands in 960 cm−1 to 930 cm−1 and 924 −1 to 920 cm−1 regions are also assigned to the CH3 rocking +C–C stretching and 103 helical chain skeletal deformation of the PLLA component, respectively. Therefore, in Fig. 2, only 806 cm−1 is fully attributed to PBS. The bands at 806 cm−1 does not overlap with any bands of PLLA, and it accurately describes the crystallization behavior of PBS. The molecular structure of PBS also shows that the corresponding CH2 groups of 806 cm−1 directly connect to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups, thereby reflecting the real C
O groups, thereby reflecting the real C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O movements of PBS. In this study, the bands at 806 cm−1 is certainly chosen as the projection. To simplify the calculations, we only select the spectral intensity at 806 cm−1 as the projection. Thus, the projection vector (not a matrix) is the spectral intensity at 806 cm−1.
O movements of PBS. In this study, the bands at 806 cm−1 is certainly chosen as the projection. To simplify the calculations, we only select the spectral intensity at 806 cm−1 as the projection. Thus, the projection vector (not a matrix) is the spectral intensity at 806 cm−1.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) O groups. Fig. 3 is the Proj-MW2D correlation FTIR spectra of PLLA/PBS upon cooling, and the spectral intensity at 806 cm−1 is the projection vector. Fig. 3(a) and (b) show the Proj-MW2D correlation spectrum and null-space Proj-MW2D correlation spectrum, respectively.
O groups. Fig. 3 is the Proj-MW2D correlation FTIR spectra of PLLA/PBS upon cooling, and the spectral intensity at 806 cm−1 is the projection vector. Fig. 3(a) and (b) show the Proj-MW2D correlation spectrum and null-space Proj-MW2D correlation spectrum, respectively.
The molecular motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups with the same motion feature as the projection vector at 806 cm−1 is retained in the Proj-MW2D correlation spectrum [Fig. 3(a)]. Results show that the correlation intensity appears at approximately 1714 cm−1, which represents the C
O groups with the same motion feature as the projection vector at 806 cm−1 is retained in the Proj-MW2D correlation spectrum [Fig. 3(a)]. Results show that the correlation intensity appears at approximately 1714 cm−1, which represents the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O motion involved in PBS crystallization. The response temperature is approximately 78 °C. This temperature is the crystallization temperature of PBS in PLLA/PBS. In the null-space Proj-MW2D correlation spectrum [Fig. 3(a)], the C
O motion involved in PBS crystallization. The response temperature is approximately 78 °C. This temperature is the crystallization temperature of PBS in PLLA/PBS. In the null-space Proj-MW2D correlation spectrum [Fig. 3(a)], the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O motion that is completely orthogonal (not identical) with the projection vector at 806 cm−1 is observed. Fig. 3(b) represents the molecular motion of the C
O motion that is completely orthogonal (not identical) with the projection vector at 806 cm−1 is observed. Fig. 3(b) represents the molecular motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of PLLA because 806 cm−1 is attributed to the PBS component. In Fig. 3(b), the corresponding correlation intensity is observed at around 1759 cm−1, and the response temperature is 98 °C. Therefore, the crystallization temperature of PLLA is 98 °C under the experimental conditions described in the present study.
O groups of PLLA because 806 cm−1 is attributed to the PBS component. In Fig. 3(b), the corresponding correlation intensity is observed at around 1759 cm−1, and the response temperature is 98 °C. Therefore, the crystallization temperature of PLLA is 98 °C under the experimental conditions described in the present study.
Aside from separating the molecular motion of functional groups from the different components, Proj-MW2D correlation analysis can also be used to assign the overlapping bands. In Fig. 3(a) and (b), it can be easily distinguished that the crystalline bands of PBS and PLLA are 1714 and 1759 cm−1, respectively. This result is similar to previous reports.37,39,41–44 However, these reports used conventional FTIR, and their experimental methods were more complex than the ones used in the present study. In addition, these reports used the pure substance to confirm the assignment of PLLA, whereas we directly specified the assignment at 1714 and 1759 cm−1 from the PLLA/PBS blend. Therefore, Proj-MW2D correlation analysis also provides a simple way to determine the spectral assignments for multiphase and multicomponent polymers.
Fig. 3(c) shows the conventional MW2D correlation FTIR spectrum of the PLLA/PBS blend for comparison. The conventional MW2D correlation FTIR spectrum is the combination of the Proj-MW2D [Fig. 3(a)] and null-space Proj-MW2D correlation FTIR spectra [Fig. 3(b)]. However, in-depth analysis shows that the conventional MW2D method can only determine two transition temperatures of PLLA/PBS upon cooling. In addition, it cannot specify the origin of the molecular motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in 1850 cm−1 to 1635 cm−1 region. The PCMW2D correlation FTIR spectra of the PLLA/PBS blend upon cooling are illustrated in Fig. 4, including synchronous [Fig. 4(a)] and asynchronous spectra [(Fig. 4(b)]. Similarly, PCMW2D can determine two transitions of PLLA/PBS at 98 °C and 78 °C, respectively. However, similar to conventional MW2D, PCMW2D also cannot specify the origin of the C
O groups in 1850 cm−1 to 1635 cm−1 region. The PCMW2D correlation FTIR spectra of the PLLA/PBS blend upon cooling are illustrated in Fig. 4, including synchronous [Fig. 4(a)] and asynchronous spectra [(Fig. 4(b)]. Similarly, PCMW2D can determine two transitions of PLLA/PBS at 98 °C and 78 °C, respectively. However, similar to conventional MW2D, PCMW2D also cannot specify the origin of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O motion at 1759 and 1714 cm−1. In Fig. 4(a), the negative correlation peaks of blue areas represent the increase in the spectral intensities at 1759 and 1714 cm−1 in the cooling direction.
O motion at 1759 and 1714 cm−1. In Fig. 4(a), the negative correlation peaks of blue areas represent the increase in the spectral intensities at 1759 and 1714 cm−1 in the cooling direction.
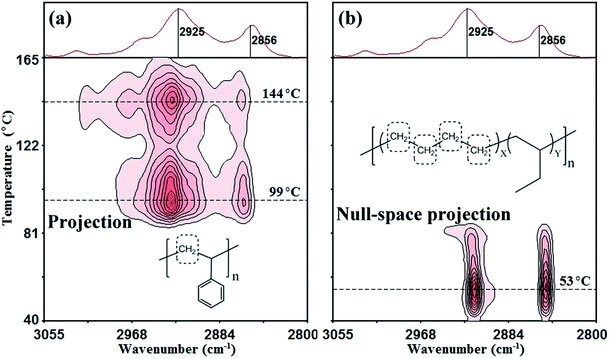
4.2. Extraction of the molecular motion of CH2 groups from ethylene units in the EB component during microcrystalline melting in PS/EB
In the null-space Proj-MW2D correlation spectra [Fig. 6(b)], the CH2 motion that is completely orthogonal (not identical) to the projection matrix is determined. That is, the molecular motion of CH2 groups is not related to the ethylene units of the EB component [Fig. 6(b)]. The correlation intensity peaks appear at 2925 and 2856 cm−1 but at high temperatures of 99 °C and 144 °C, respectively. Two transition temperatures represent the molecular motion of CH2 groups of the main chain from the PS component. According to the literature,53–62 99 °C is the glass transition temperature of PS.53–57 The temperature at 144 °C represents a liquid–liquid transition. Previous studies attributed this transition to the viscous flow of PS.58–62
Fig. 6(c) shows the conventional MW2D correlation FTIR spectrum, which is a combination of the Proj-MW2D and null-space Proj-MW2D correlation spectra. The correlation intensity peaks appear at 2925 and 2856 cm−1, and the corresponding temperatures are 53 °C, 99 °C, and 144 °C. Although three transition temperatures can be observed, the conventional method cannot separate the molecular motion of CH2 groups from EB or PS component without the help of other characterization methods. The conventional MW2D correlation FTIR spectra cannot indicate the source component of the transitions at the functional group level.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH of benzene rings.51 In the present study, the spectral intensity within 710 cm−1 to 687 cm−1 region (698 cm−1 as the center) is selected as the projection matrix. Within the entire temperature-dependent FTIR spectrum (Fig. 5), the bands within 710 cm−1 to 687 cm−1 are characteristic of the PS component. The spectral intensities of these bands are relatively large and do not coincide with any of bands of the EB component. Therefore, 710 cm−1 to 687 cm−1 (698 cm−1 as the center) is a suitable projection matrix for extracting the CH2 motion from PS component.
CH of benzene rings.51 In the present study, the spectral intensity within 710 cm−1 to 687 cm−1 region (698 cm−1 as the center) is selected as the projection matrix. Within the entire temperature-dependent FTIR spectrum (Fig. 5), the bands within 710 cm−1 to 687 cm−1 are characteristic of the PS component. The spectral intensities of these bands are relatively large and do not coincide with any of bands of the EB component. Therefore, 710 cm−1 to 687 cm−1 (698 cm−1 as the center) is a suitable projection matrix for extracting the CH2 motion from PS component.The Proj-MW2D and null-space Proj-MW2D correlation FTIR spectra are shown in Fig. 7(a) and (b), respectively. The molecular motion with the same motion feature as the projection matrix (710 cm−1 to 687 cm−1) is retained in Fig. 7(a). Once again, the molecular motion of CH2 groups from the PS component is successfully separated. These results confirm that the correlation intensity peaks of 2925 and 2856 cm−1 at 99 °C and 144 °C are the CH2 motion of the main chain from the PS component. Fig. 7(a) is almost the same as Fig. 6(b). Different from Fig. 6(b) and 7(b) shows that the molecular motion of CH2 groups of the ethylene units from the EB component is extracted in the null-space Proj-MW2D correlation FTIR spectrum. Similar to Fig. 6(a) and 7(b) shows that the correlation intensity peaks of 2925 and 2856 cm−1 appear at 53 °C. The use of 710 cm−1 to 687 cm−1 (698 cm−1 as the center) as the projection matrix can also separate the molecular motion of CH2 groups generated from the PS component.
5. Conclusions
Proj-MW2D was developed to separate the molecular motion of groups generated from different components or phases for multicomponent and multiphase polymers. The specific implementation steps for Proj-MW2D were enumerated after the theoretical derivation and algorithm research.Two types of two-component blends, namely, PLLA/PBS and PS/EB, were employed to validate the concept of separating the molecular motion of groups. The molecular motion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups from the crystalline phase in the PBS component was successfully extracted through the Proj-MW2D correlation FTIR spectra of PLLA/PBS upon cooling. The characteristic bands at 806 cm−1 of PBS was used as the projection vector. Meanwhile, the molecular motion of C
O groups from the crystalline phase in the PBS component was successfully extracted through the Proj-MW2D correlation FTIR spectra of PLLA/PBS upon cooling. The characteristic bands at 806 cm−1 of PBS was used as the projection vector. Meanwhile, the molecular motion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups from the PLLA component was separated in the null-space Proj-MW2D correlation FTIR spectrum. The PBS crystalline phase showed the C
O groups from the PLLA component was separated in the null-space Proj-MW2D correlation FTIR spectrum. The PBS crystalline phase showed the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O motion at 78 °C. The molecular motion of C
O motion at 78 °C. The molecular motion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups was generated from the PLLA component at 98 °C.
O groups was generated from the PLLA component at 98 °C.
The molecular motion of CH2 groups during the microcrystalline melting of the ethylene units from the EB component was successfully extracted at 53 °C using the Proj-MW2D correlation FTIR spectra of PS/EB upon heating. The projection matrix was the spectral intensity of 730 cm−1 to 712 cm−1 (720 cm−1 as the center). The molecular motion of CH2 groups of the main chain in the PS component was separated in the null-space Proj-MW2D correlation FTIR spectrum at 99 °C and 144 °C.
This study successfully used the Proj-MW2D correlation technique to separate the molecular motion of groups for multiphase and multicomponent polymers. This method allows researchers to study the mechanism of the complex transition process for multiphase and multicomponent polymer systems.
In the future, Proj-MW2D can be extended to three- or four-component polymers, to other materials (e.g., small organic, biological, inorganic, and non-metallic materials), and to other spectra (e.g., Raman, X-ray, and UV). In addition, the projection technique was directly applied to MW2D correlation spectroscopy in this study. Nevertheless, it can be incorporated into PCMW2D methods and other forms of moving-window methods.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant no. 51473104, 51003066), State Key Laboratory of Polymer Materials Engineering (Grant no. sklpme2014-3-06), and the Outstanding Young Scholars Foundation of Sichuan University (Grant no. 2011SCU04A13).Notes and references
- T. R. Crompton, Characterisation of Polymers, Smithers Rapra Technology Limited, Shrewsbury, 2008 Search PubMed.
- T. Theophanides, Infrared Spectroscopy-Materials Science, Engineering and Technology, InTech, Rijeka, 2012 Search PubMed.
- B. Stuart, Infrared Spectroscopy: Fundamentals and Applications, John Wiley & Sons, 2004 Search PubMed.
- I. Noda, Appl. Spectrosc., 1993, 47, 1329–1336 CrossRef CAS.
- I. Noda and Y. Ozaki, Two-dimensional Correlation Spectroscopy - Applications in Vibrational and Optical Spectroscopy, John Wiley & Sons, Chichester, 2004 Search PubMed.
- I. Noda, J. Mol. Struct., 2006, 799, 2–15 CrossRef CAS PubMed.
- I. Noda, J. Mol. Struct., 2008, 883–884, 2–26 CrossRef CAS PubMed.
- I. Noda, J. Mol. Struct., 2010, 974, 3–24 CrossRef CAS PubMed.
- X. Liu, T. Zhou, X. Wang and J. Zhang, Anal. Bioanal. Chem., 2010, 397, 339–343 CrossRef CAS PubMed.
- H. Lee, Y. M. Jung, K. I. Lee, H. S. Kim and H. S. Park, RSC Adv., 2013, 3, 25944–25949 RSC.
- Z. W. Wang and P. Y. Wu, RSC Adv., 2012, 2, 7099–7108 RSC.
- M. Thomas and H. H. Richardson, Vib. Spectrosc., 2000, 24, 137–146 CrossRef CAS.
- S. Morita, H. Shinzawa, R. Tsenkova, I. Noda and Y. Ozaki, J. Mol. Struct., 2006, 799, 111–120 CrossRef CAS PubMed.
- H. H. Richardson and D. Wang, J. Mol. Struct., 2010, 974, 52–55 CrossRef CAS PubMed.
- S. Sasic, Y. Katsumoto, N. Sato and Y. Ozaki, Anal. Chem., 2003, 75, 4010–4018 CrossRef CAS.
- L. Hou and P. Y. Wu, RSC Adv., 2014, 4, 39231–39241 RSC.
- T. Zhou, A. Zhang, C. S. Zhao, H. W. Liang, Z. Y. Wu and J. K. Xia, Macromolecules, 2007, 40, 9009–9017 CrossRef CAS.
- T. Zhou, Z. Y. Wu, Y. Y. Li, J. A. Luo, Z. G. Chen, J. K. Xia, H. W. Liang and A. M. Zhang, Polymer, 2010, 51, 4249–4258 CrossRef CAS PubMed.
- Y. Liu, W. L. Li, L. Hou and P. Y. Wu, RSC Adv., 2014, 4, 24263–24271 RSC.
- S. Morita, H. Shinzawa, I. Noda and Y. Ozaki, Appl. Spectrosc., 2006, 60, 398–406 CrossRef CAS PubMed.
- J. A. Luo, T. Zhou, X. L. Fu, H. W. Liang and A. M. Zhang, Eur. Polym. J., 2011, 47, 230–237 CrossRef CAS PubMed.
- Z. Chen, T. Zhou, J. Hui, L. Li, Y. Li, A. Zhang and T. Yuan, Vib. Spectrosc., 2012, 62, 299–309 CrossRef CAS PubMed.
- Y. Li, T. Zhou, Z. Chen, J. Hui, L. Li and A. Zhang, Polymer, 2011, 52, 2059–2069 CrossRef CAS PubMed.
- J. Shi, P. Wu and F. Yan, Langmuir, 2010, 26, 11427–11434 CrossRef CAS PubMed.
- S. Sun, W. Zhang, W. Zhang, P. Wu and X. Zhu, Soft Matter, 2012, 8, 3980–3987 RSC.
- S. Sun and P. Wu, Macromolecules, 2013, 46, 236–246 CrossRef CAS.
- I. Noda, J. Mol. Struct., 2010, 974, 116–126 CrossRef CAS PubMed.
- I. Noda, J. Mol. Struct., 2010, 974, 108–115 CrossRef CAS PubMed.
- H. Shinzawa, K. Awa, I. Noda and Y. Ozaki, Vib. Spectrosc., 2013, 65, 28–35 CrossRef CAS PubMed.
- M. K. Kim, S. R. Ryu, I. Noda and Y. M. Jung, Vib. Spectrosc., 2012, 60, 163–167 CrossRef CAS PubMed.
- G. H. Golub and C. F. Van Loan, Matrix Computations, Johns Hopkins University Press, Baltimore, 1996 Search PubMed.
- L. Zheng, C. Li, D. Zhang, G. Guan, Y. Xiao and D. Wang, Polym. Degrad. Stab., 2010, 95, 1743–1750 CrossRef CAS PubMed.
- H.-P. Zhao, J.-T. Zhu, Z.-Y. Fu, X.-Q. Feng, S. Yue and R.-T. Ma, Thin Solid Films, 2008, 516, 5659–5663 CrossRef CAS PubMed.
- Y. J. Phua, N. S. Lau, K. Sudesh, W. S. Chow and Z. A. Mohd Ishak, Polym. Degrad. Stab., 2012, 97, 1345–1354 CrossRef CAS PubMed.
- J. Zhang, K. Tashiro, H. Tsuji and A. J. Domb, Macromolecules, 2008, 41, 1352–1357 CrossRef CAS.
- H.-S. Kim, H.-J. Kim, J.-W. Lee and I.-G. Choi, Polym. Degrad. Stab., 2006, 91, 1117–1127 CrossRef CAS PubMed.
- H. S. Lee, H. D. Park and C. K. Cho, J. Appl. Polym. Sci., 2000, 77, 699–709 CrossRef CAS.
- C. Yan, Y. Zhang, Y. Hu, Y. Ozaki, D. Shen, Z. Gan, S. Yan and I. Takahashi, J. Phys. Chem. B, 2008, 112, 3311–3314 CrossRef CAS PubMed.
- J. Zhang, C. Li, Y. Duan, A. J. Domb and Y. Ozaki, Vib. Spectrosc., 2010, 53, 307–310 CrossRef CAS PubMed.
- P. Opaprakasit, M. Opaprakasit and P. Tangboriboonrat, Appl. Spectrosc., 2007, 61, 1352–1358 CrossRef CAS PubMed.
- E. Meaurio, E. Zuza, N. López-Rodríguez and J. R. Sarasua, J. Phys. Chem. B, 2006, 110, 5790–5800 CrossRef CAS PubMed.
- Y. Cai, J. Lv and J. Feng, J. Polym. Environ., 2013, 21, 108–114 CrossRef CAS.
- V. Krikorian and D. J. Pochan, Macromolecules, 2005, 38, 6520–6527 CrossRef CAS.
- J. Zhang, Y. Duan, H. Sato, H. Tsuji, I. Noda, S. Yan and Y. Ozaki, Macromolecules, 2005, 38, 8012–8021 CrossRef CAS.
- J. C. Sworen, J. A. Smith, J. M. Berg and K. B. Wagener, J. Am. Chem. Soc., 2004, 126, 11238–11246 CrossRef CAS PubMed.
- K. Jokela, A. Väänänen, M. Torkkeli, P. Starck, R. Serimaa, B. Löfgren and J. Seppälä, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 1860–1875 CrossRef CAS.
- B. Crist and E. S. Claudio, Macromolecules, 1999, 32, 8945–8951 CrossRef CAS.
- S. Krimm, Adv. Polym. Sci., 1960, 2, 51–172 CrossRef CAS.
- K. Holland-Moritz and E. Sausen, J. Polym. Sci., Polym. Phys. Ed., 1979, 17, 1–23 CrossRef CAS.
- T. Ishioka, H. Wakisaka, I. Kanesaka, M. Nishimura and H. Fukasawa, Polymer, 1997, 38, 2421–2430 CrossRef CAS.
- P. Sharma, P. Tandon and V. D. Gupta, Eur. Polym. J., 2000, 36, 2629–2638 CrossRef CAS.
- Y. Naka, N. Nemoto and Y. Song, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 1520–1531 CrossRef CAS.
- R. J. Roe and J. J. Curro, Macromolecules, 1983, 16, 428–434 CrossRef CAS.
- B. Vorselaars, A. V. Lyulin and M. A. J. Michels, Macromolecules, 2007, 40, 6001–6011 CrossRef CAS.
- J. D. Menczel and R. B. Prime, Thermal Analysis of Polymers, Fundamentals and Applications, John Wiley & Sons, Hoboken, 2009 Search PubMed.
- T. Hatakeyama and Z. H. Liu, Handbook of thermal analysis, John Wiley & Sons, Chichester, 1998 Search PubMed.
- P. Painter, M. Sobkowiak and Y. Park, Macromolecules, 2007, 40, 1730–1737 CrossRef CAS.
- C. Y. Liu and H. Morawetz, Macromolecules, 1988, 21, 515–518 CrossRef CAS.
- T. Kanaya, T. Kawaguchi and K. Kaji, J. Chem. Phys., 1996, 104, 3841–3850 CrossRef CAS PubMed.
- S. Shang, X. Wu and Z. Zhu, Phys. B, 2007, 396, 160–163 CrossRef CAS PubMed.
- S. Shuying, Z. Zhenguang, L. Zaijun and Z. Guangzhao, J. Phys.: Condens. Matter, 2007, 19, 416107 CrossRef.
- T. Zhou, L. Peng, Y. Liu, A. Zhang and Y. Huang, J. Mol. Struct., 2014, 1059, 8–14 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |