Theoretical studies of a 3D-to-planar structural transition in Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters

Abstract

Basin-hopping global searching and quantum chemistry calculations were performed to predict global minimum structures of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters in order to explore the intrinsic mechanism of 3D-to-planar structural transition and structural characteristics of planar tetracoordinate species. A structural similarity of isoelectronic Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters exists, and may generally be extended to similar clusters containing B, C, N, O, and P. The structural diagram and molecular orbital analysis reveal that a 3D-to-planar structural transition should be related to composition and total valence electron number of clusters. Our calculations indicate that the global minima of Si_nAl_5−n^+1,0,−1 (n = 0–5) with planar tetracoordinate Si (ptSi) should meet the 18-electron rule and take the charge of −1, 0, +1. Further, it is found that 18-electron M–Al₄ (M = B, C, N, O, and F) planar clusters prefer a central atom M with a low electronegativity and peripheral Al substituted with a lower-electronegativity atom. Based on the structural characteristics of planar clusters, we firstly predict a novel planar tetracoordinate C (PtC) structure C₂Al₃⁻ which is more stable in energy than the experimentally observed CAl₄²⁻. C₂Al₃⁻ may become a building block to assemble some larger supermolecule containing multiple planar hypercoordinate C (phC).

---

1. Introduction

Since Hoffmann et al. first predicted the possible existence of “planar tetracoodinate carbon (ptC)” in the early 1970s,¹ there has been a substantial research effort in theory and experiment to design new structures for planar hypercoordinated carbon (tetra-, penta-, hexa-, and heptacoordinate C) and assemble complicated 2D and 3D functional materials based on these structures with planar hypercoordinated elements (phE).^2–14 In the past two decades, a large number of ptC structures have been theoretically predicted.^2,12 However, many of them were further demonstrated in experiment not to be global minima.^15,16 Therefore, there is widespread interest in the chemical community to accurately predict a global minimum structure containing phE.

Several theories were developed to predict the stable structures containing phE. In 1970, Hoffmann et al. firstly suggested that ptC could be stabilized by introducing σ-donating/π-accepting substituents to delocalize the lone-pair electrons on the central C.¹ In the past two decades, such an electronic stabilization mechanism achieved a success in theoretically predicting the ptC structures of CAl₂Ge₂ and CGa₂Si₂,¹⁷ and experimentally identifying the ptC and ptSi structures such as CAl₄⁻,¹⁸ CAl₃Si⁻,¹⁹ CAl₃Ge⁻,¹⁹ CAl₄²⁻,²⁰ and SiAl₄⁻.²¹ For these larger carbon–boron clusters, the global minima of CB₆²⁻, CB₇⁻, and CB₈ initially were predicted in theory to take structures containing planar hypercoordinated carbon (phC).^15,16 However, experimental and theoretical studies indicated that carbon was very likely to avoid the central hypercoordinated position, taking phB structures. In 2010, combining experimental and theoretical studies, Wang et al. revealed a planar-to-linear structural transition of C_xB_5−x⁻ global minima is fully dependent on their composition.²² However, such a structural transition rule is still difficult to be applied to predict the structural characteristic of unidentified clusters because there are many unknown factors such as charge of cluster, different atom distribution, and boundary of structural transition. Understanding structural transition mechanism and reveal structural characteristic of phE clusters plays an important role in predicting a stable phE cluster.

The previous studies indicated that Si₅^+1,0,−1 clusters have trigonal bipyramid structure and Al₅^−1,0 clusters have planar tetracoordinate structure.^23,24 In 2000, the joint experimental and computational effort by Boldyrev et al. identified SiAl₄⁻ as the first and only available observation of ptSi molecule.²¹ Later, although many ptSi species were predicted in theory,^25–35 experimental confirmation of these global minima has been elusive. It is expected that a 3D-to-planar structural transition should exist in Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters due to different structure characteristic of Al₅^−1,0 and Si₅^+1,0,−1 clusters. Further, the stable analysis for extensive structures can yield deep insight into transition mechanism and structural characteristic of phE clusters.

In this paper, we performed extensive quantum chemistry calculations to predict global minimum structures of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters using the basin-hopping algorithm.^36,37 By analyzing relative stability, structural characteristic and molecular orbitals of these global minima, we expect to reveal intrinsic mechanism of 3D-to-planar structural transition. Further, we calculated the various derivative planar structures of M–Al₄ (M = B, C, N, O, and F) to elucidate structural characteristic of phE clusters. Finally, some new phC clusters are predicted based on the identified structure-stability relation. Therefore, the present study provides deep insight into the structural characteristic of phE clusters and is helpful to understand non-classical chemical bonding.

2. Computational methods

The basin-hopping global-searching algorithm combined with the B3LYP/6-31G optimization was used to sample the potential energy surfaces of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters.^36,37 The effectiveness of basin-hopping algorithm was demonstrated.^38,39 After the initial search, further geometrical optimization was performed to obtain more accurate geometrical and energetic information by using the same hybrid method (B3LYP) and applying polarized split-valence triple-ξ augmented with diffuse function basis set 6-311+G(2d). The additional MP2/aug-cc-pvtz calculations were performed to confirm structural and energetic consistency with the B3LYP calculation results. Vibrational frequency analysis was carried out to check whether the optimized structures are true minima or saddle points. To obtain more accurate relative energy of the optimized structure, we carried out high level single-point calculations for all B3LYP-optimized structures at the CCSD(T)/6-311+G(2d) level. All calculations in this work were performed by using Gaussian 09 package.⁴⁰

3. Results and discussion

3.1 Global minimum structures of Si_nAl_5−n^+1,0,−1

We collected all B3LYP-optimized structures and their relative energies of Si_nAl_5−n⁺, Si_nAl_5−n, and Si_nAl_5−n⁻ clusters in Fig. S1, S2, and S3,† respectively. The optimized structures of these clusters are labeled by Si_nAl_5−n-m where m represents the order of relative stability. These local and global minima exhibit rich structural variation including planarity, distorted planarity, hexahedron, and triangular dipyramid, and so on. In 2000, Wang et al. determined fan-shaped structures of Al₅, Al₅⁻, SiAl₄, and SiAl₄⁻ clusters based on their experimental and theoretical studies. They also concluded that a four-center peripheral bond played an important role in stabilizing their planar structures.^21,24,41 To determine the accuracy of our calculation, we compared our calculated geometries and relative energies with corresponding experimental and computational results.^21,24,41 Our calculated results are consistent with the previous report. In addition, we also performed triplet and quartet calculations for Si₃Al₂-1 and Si₂Al₃-1 clusters, respectively in order to check multiplicity effect of stability. Our calculations show that these clusters with high spin states are highly unstable with 22.05 and 21.94 kcal mol⁻¹ higher in energy than the corresponding low spin structures, respectively. This suggests that the ground state of these clusters should correspond to the lowest spin state of multiplicity.

In order to elucidate a structural transition mechanism of clusters, all global minimum structures identified in our calculation are collected in Fig. 1. The structures with the same charge state but different composition are arranged in the same column. In terms of Si_nAl_5−n and Si_nAl_5−n⁻, the structural transition from planar to tetrahedral structures can be observed with the change of composition. The 3D-to-planar transition points of Si_nAl_5−n and Si_nAl_5−n⁻ global minima occur in n = 3–4 and n = 2–3, respectively. In comparison, Wang et al. also observed a planar-to-linear transition of C_xB_5−x⁻ (x = 1–5) global minima according to their joint experimental and theoretical studies.²² They explained the structural transition from a mixture of doping C atoms in planar B₅⁻ to doping B atoms in linear C₅⁻. However, such a structural transition with a function of composition does not occur in the global minima of Si_nAl_5−n⁺. The global minima of pure species, Al₅⁺ and Si₅⁺, possess 3D structures, while those of mixing species of Si_nAl_5−n⁺ (n = 1–4) exhibit planar structure. Therefore, it is necessary to explore a more comprehensive structural transition mechanism of these structure-mixing clusters.

Fig. 1 Optimized global minimum structures of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters. The isoelectronic structures are connected by arrowed line. The structural symmetries are given. Bond lengths are presented in unit of Å.

As shown in Fig. 1, the isoelectronic clusters are connected by the arrowed lines. It indicates that the structural similarity of isoelectronic global minima exists in all these calculated clusters. In terms of Si_nAl_5−n^−1,0,+1 (n = 0–5) clusters, the global minima with 15–18 valence electrons have ptSi structures except for Si₂Al₃⁺, while those with 14, 19, and 20 valence electrons do 3D structures. In fact, the structural similarity of isoelectronic clusters could be verified by previously reported C_mB_n and C_mB_n⁻ (m = 1–4; n = 4–8)¹² and XAl_nSi_4−n (X = O, N, C, B; n = 1–4) clusters.⁴² It is worth mentioning that the structural similarity may be limited in the isoelectronic clusters formed by the main elements, for example, C–B, C–N, C–Al, C–Si, Si–Al, Si–P, and Al–P. The involvement of d-electrons may generate different structural characteristic.

In the past years, the C position in the planar C–B clusters, center or periphery, captures extensive research interest in experiment and theory.^8,9,43–46 A series of experimental and theoretical studies showed that in CB₄, CB₄⁻, CB₆²⁻, CB₇⁻, CB₈, and CB₈⁻ clusters C atom preferred a peripheral position and B atom in a central hypercoordinate position.^15,16 In contrast, CB₄⁺ was theoretically and experimentally determine to take a ptC structure that is a little more stable than ptB.^12,42 Our calculations identified that the global minima of Si_nAl_5−n^+1,0,−1 (n = 0–5) with total 16–18 valence electrons preferred ptSi structures which have much lower energies than the corresponding ptAl (planar tetracoordinate Al) structures.

In addition, the global minima of Si₃Al₂⁺ and Si₄Al⁺ have kite-shaped structures containing ptSi, which are ∼16.0 kcal mol⁻¹ lower in energy than the corresponding fan-shaped structures with ptSi. To the best of our knowledge, it is first time to report this kite-shaped structures containing ptSi so far. Electron structure analysis indicates that these kite-shaped structures with ptSi are formed as a result of reducing electron occupancy of 3c–2e bond in the Al–Si–Al structure.

3.2 Structural stability of ground state clusters

Although the structural similarity of isoelectronic clusters is established based on our calculated global minimum structures, their relative stability is unclear. On the basis of our calculated structures and energies, a structural diagram of neutral and charged Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters is constructed and shown in Fig. 2. The relative energies of Si_nAl_5−n clusters were calculated based on the equation of E_re = (E_SinAl5−n − nE_Si − (5 − n)E_Al)/5, where E_Si and E_Al are atomic energies of Si and Al. The structural diagram presents the relation of relative energies with composition, charge state, and valence electron number. First of all, a dissociation region is roughly plotted based on our extensive calculation for Si_nAl_5−n²⁺ (n = 1–4) clusters that presents a dissociation state. As a result, 3D structures are presented in these regions with the relatively low (≤14e⁻) and high valence electron (≥19e⁻). Secondly, our calculations for SiAl₄²⁻ and Al₅²⁻ show that high charge state of these clusters may not be very stable compared with the corresponding clusters in a lower charge state (SiAl₄⁻ and Al₅⁻). Therefore, it is expected that the ptSi global minima of Si_nAl_5−n (n = 0–5) clusters are generally restricted in the charge states of −1, 0, and +1 and with the total valence electrons of 15–18.

Fig. 2 The structural diagram of relative energies, total valence electron number, and composition of global minimum structures of Si_nAl_5−n^+1,0,−1 (n = 0–5). The relative energies are calculated based on the ground state energies of Si and Al atoms.

As shown in Fig. 2, the calculated clusters in the same charge state (see dash lines) have gradually decrease relative energies with increasing Si concentration in the Si_nAl_5−n (n = 0–5) clusters. This indicates that introduction of Si in the planar Al₅ makes clusters more stable, which may be ascribed to a stronger Al–Si bond. In contrast, the isoelectronic clusters have approximately increased relative energies with increasing Si concentration in the Si_nAl_5−n^+1,0,−1 clusters. In terms of thermodynamic stability, the anion cluster Si₂Al₃⁻¹ with 18 valence electrons is the most stable among all calculated Si_nAl_5−n^+1,0,−1 clusters.

Further, the interconversion transition state between the stable 3D and planar structures were calculated to elucidate relative stability of these ptSi cluster. The DFT-calculated profile of transition paths are presented in Fig. 3. It is worth noting that only neutral clusters are considered in order to reduce computational cost. But the transition trend in the neutral system may be consistent with those in the charged clusters. As shown in Fig. 3, the transition barriers from planar to 3D structures of Si₃Al₂, Si₂Al₃, SiAl₄, Si₄Al, and Si₅, corresponding to 18e, 17e, 16e, 19e, and 20e, are calculated as 22.51, 18.29, 14.98, 7.64, and 6.35 kcal mol⁻¹, respectively. This indicates that the planar structure of Si₃Al₂ is the most stable, which is consistent with our previously identified 18-electron rule.

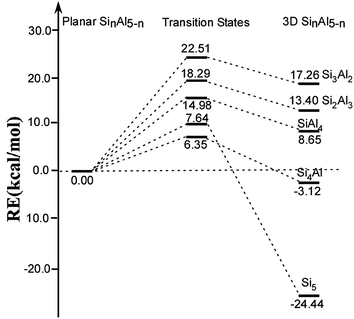Fig. 3 Energy profile of structural transitions between the most stable planar structure and 3D structures of neutral Si_nAl_5−n (n = 0–5) species.

3.3 Molecular orbital analysis

To understand the origin of structural similarity of isoelectronic clusters, we performed molecular orbital (MO) analysis for neutral Si_nAl_5−n (n = 0–3) structures containing ptSi. Fig. 4 presents their frontier MOs which play an important role in determining the structural stability of cluster. From Al₅ to Si₂Al₃, the shapes of frontier MOs are not changed too much with Si introduced. There are two categories of molecular orbitals for planar Al₅ cluster. On one hand, HOMO−2 (π) and LUMO (σ) of Al₅ take a role in stabilizing the central triangle structure and are favorable to stabilize the planar structure of Al₅ cluster. On the other hand, HOMO−1 and HOMO of Al₅ are formed by p-orbitals of peripheral atoms interacting with the orbitals of triangle structure make significant contribution on the planar-to-3D structural transition. LUMO+1 with antibonding characteristic disfavors planar structure. Therefore, adding up to 3 electrons into Al₅ still can maintain stability of planar structure, which is equivalent to a composition change from Al₅ to Si₃Al₂. However, more electrons added into LUMO+1 of Al₅ may make the planar structure unstable. It is consistent with our previous conclusion of ptSi structures with 15–18 valence electrons and the most stable structure meeting 18-electron rule.

Fig. 4 The frontier molecular orbitals of global minimums of neutral Si_nAl_5−n (n = 0–3) clusters. The iso-surface values are in 0.025 e per au.

Based on our structural diagram analysis, it is found that composition and total valence electron number of clusters synergistically play an important role in determining structural characteristic and stability of ptSi structures. The Si_nAl_5−n clusters with 15–18 valence electrons present planar structure and those with 19–20 valence electrons do 3D structure. Molecular orbital analysis indicates that the structural transition is attributed to the bonding pattern change from planar-favored bonding orbitals filled by up to 18 electrons to planar-disfavored antibonding orbitals filled by over 18 electrons.

3.4 Predicting some stable ptE clusters

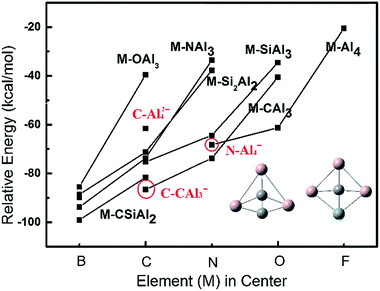
Based on our extensive calculations including structural stability and molecular orbital analysis, one can easily summarize that the ptE clusters derived from planar Al₅ must meet the 18-electron rule for maintaining the planarity of structure. Also, most of ptE clusters have the charge states of −1, 0, and +1. Accordingly, a series of ptE clusters with the formula of M–Si_nAl_4−n^+1,0,−1 (M = B, C, N, O, and F; n = 0–4) are predicted at the theory level of B3LYP/6-311+G(2d). The relative energies and optimized structures of these ptE clusters are presented in Fig. 5. Due to the small atomic size of the elements in center, the square or square-like structures are obtained instead of fan-shaped structure, as shown in the inset of Fig. 5. When an element of the second row in the period table is inserted into the peripheral skeleton, the square-shaped structure is changed into the triangle-shaped structure due to a strong chemical bonding between two small atoms. The solid lines are used to connect the structures with the same peripheral skeleton, but different element in center. As shown in Fig. 5, the calculated planar clusters in the same of central element have a reduced stability with a larger electronegativity of atom introduced into peripheral skeleton, which is consistent with isoelectronic Si_nAl_5−n^−1,0,+1 (n = 0–5) clusters. Under the same peripheral skeleton, the relative energies of planar clusters are decreased with changing to a larger electronegative central atom. In all optimized planar structures with 18 electrons, B–CSiAl₂⁻ is determined as the most stable cluster with the formation energy of 99.07 kcal mol⁻¹.

Fig. 5 The DFT-calculated relative energies of M–Si_nAl_4−n^+1,0,−1 (the central element M = B, C, N, O, and F; n = 0–4) clusters with 18-electron. The solid lines connect the structures with the same peripheral skeleton, but different element in center. The schematic structures in our calculations are presented in the inset.

Although B–CSiAl₂⁻ is identified as the most stable cluster in our calculations, its preparation may be very difficult since four compositions required in the ptB cluster. The relative energies of three planar species, C–Al₄²⁻, C–CAl₃⁻, and N–Al₄⁻, are labeled in Fig. 5. All these species are formed by two compositions and may be more practical to synthesize experimentally. Among three species, C–CAl₃⁻ is found to have the largest formation energies of −86.62 kcal mol⁻¹, which has 29.52 kcal mol⁻¹ lower in energy than the typical ptC species C–Al₄²⁻ identified in experiment.^18–20

Based on the building block of C–CAl₃⁻, two planar species C₂–Al₄ and C₃–Al₆ were obtained by geometric optimization and the corresponding relative energies are −74.85 and −76.63 kcal mol⁻¹, respectively. As indicated in Fig. 6, the C₂–Al₄ and C₃–Al₆ clusters have the structural characteristic of ptC and phC, respectively. Further, molecular orbital analysis reveals that the electrons of antibonding π orbitals in C–C and C–C–C fragments in these structures are delocalized to surrounding Al–Al and Al–C bonding orbitals. These frontier molecular orbitals play an important role in stabilizing planar structures of species. Unfortunately, so far these ptC and phC clusters were not reported experimentally and theoretically. It is expected that these ptC and phC clusters can be prepared in a future experiment.

Fig. 6 The optimized structures, relative energies, and frontier molecular orbitals of C–CAl₃⁻, C₂–Al₄, and C₃–Al₆ species. The iso-surface values of these molecular orbitals are in 0.025 e per au.

4. Conclusions

In this paper, we sampled the potential energy surfaces of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters by means of the basin-hopping algorithm combined with the DFT optimization. After the initial searching, more accurate quantum chemistry calculations for these clusters were carried out to obtain the global minimum structures in order to elucidate underlying 3D-to-planar structural transition mechanism and structural characteristic of ptE clusters. Our calculations indicate that the 3D-to-planar structural transition of Si_nAl_5−n^+1,0,−1 (n = 0–5) clusters is related to composition and total valence electron number of clusters. The structural stability and molecular orbital analysis show that the global minima with ptSi prefer the charge states of −1, 0, and +1 and total valence electrons of 18. In terms of an 18-electron M–Al₄ cluster containing ptE, a central atom M with a low electronegativity and peripheral Al substituted with low-electronegativity atom should be stable. Based on the structural characteristic, we further predict a novel ptC structure C–CAl₃⁻ which is more stable in energy than the observed C–Al₄²⁻ in experiment. It may become a building block to construct a larger supermolecule containing ptC structure.

Acknowledgements

This work is financially supported by “One-Hundred-Talent Project” and “the Key Research Program (Grant no. KGZD-EW-T06)” of the Chinese Academy of Sciences.

References

1. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
2. K. Exner and P. V. Schleyer, Science, 2000, 290, 1937–1940.
3. P. D. Pancharatna, M. A. Mendez-Rojas, G. Merino, A. Vela and R. Hoffmann, J. Am. Chem. Soc., 2004, 126, 15309–15315.
4. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
5. W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371.
6. L. M. Yang, Y. H. Ding and C. C. Sun, J. Am. Chem. Soc., 2007, 129, 658–665.
7. Y. Pei, W. An, K. Ito, P. V. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400.
8. X. J. Wu, Y. Pei and X. C. Zeng, Nano Lett., 2009, 9, 1577–1582.
9. M. H. Wu, Y. Pei and X. C. Zeng, J. Am. Chem. Soc., 2010, 132, 5554–5555.
10. L. M. Yang, Y. H. Ding and C. C. Sun, J. Am. Chem. Soc., 2007, 129, 1900–1901.
11. Z. X. Wang and P. V. Schleyer, Science, 2001, 292, 2465–2469.
12. Y. Pei and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 2580–2592.
13. J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778.
14. G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
15. B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250.
16. L. M. Wang, W. Huang, B. B. Averkiev, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2007, 46, 4550–4553.
17. A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972.
18. X. Li, L. S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
19. L. S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
20. X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3633.
21. A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3307–3310.
22. J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778.
23. C. Y. Zhao and K. Balasubramanian, J. Chem. Phys., 2002, 116, 3690–3699.
24. G. D. Geske, A. I. Boldyrev, X. Li and L. S. Wang, J. Chem. Phys., 2000, 113, 5130–5133.
25. S. D. Li, C. Q. Miao, J. C. Guo and G. M. Ren, J. Am. Chem. Soc., 2004, 126, 16227–16231.
26. R. Islas, T. Heine, K. Ito, P. V. R. Schleyer and G. Merino, J. Am. Chem. Soc., 2007, 129, 14767–14774.
27. P. V. Schleyer and A. E. Reed, J. Am. Chem. Soc., 1988, 110, 4453–4454.
28. P. Belanzoni, G. Giorgi, G. F. Cerofolini and A. Sgamellotti, J. Phys. Chem. A, 2006, 110, 4582–4591.
29. P. Belanzoni, G. Giorgi, G. F. Cerofolini and A. Sgamellotti, Theor. Chem. Acc., 2006, 115, 448–459.
30. W. Tiznado, N. Perez-Peralta, R. Islas, A. Toro-Labbe, J. M. Ugalde and G. Merino, J. Am. Chem. Soc., 2009, 131, 9426–9431.
31. D. Szieberth, M. Takahashi and Y. Kawazoe, J. Phys. Chem. A, 2009, 113, 707–712.
32. J. C. Guo and S. D. Li, J. Mol. Struct.: THEOCHEM, 2007, 816, 59–65.
33. S. D. Li, G. M. Ren and C. Q. Miao, Inorg. Chem., 2004, 43, 6331–6333.
34. S. D. Li, J. C. Guo, C. Q. Miao and G. M. Ren, J. Phys. Chem. A, 2005, 109, 4133–4136.
35. T. Heine and G. Merino, Angew. Chem., Int. Ed., 2012, 51, 4275–4276.
36. D. Schebarchov and D. J. Wales, Phys. Rev. Lett., 2014, 113, 156102–156106.
37. D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
38. S. Yoo, J. J. Zhao, J. L. Wang and X. C. Zeng, J. Am. Chem. Soc., 2004, 126, 16845–16849.
39. S. Bulusu, X. Li, L. S. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326–8330.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
41. C. Y. Zhao and K. Balasubramanian, J. Chem. Phys., 2002, 116, 10287–10296.
42. P. V. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 1536–1538.
43. Z. H. Cui, M. Contreras, Y. H. Ding and G. Merino, J. Am. Chem. Soc., 2011, 133, 13228–13231.
44. L. M. Wang, B. B. Averkiev, J. A. Ramilowski, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2010, 132, 14104–14112.
45. J. X. Liang, W. H. Jia, C. J. Zhang and Z. X. Cao, Acta Phys. Chim. Sin., 2009, 25, 1847–1852.
46. B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250.

---

Footnote

† Electronic supplementary information (ESI) available: All optimized geometries of global and local minima of neutral and charged Si_nAl_5−n^+1,0,−1 (n = 0–5). See DOI: 10.1039/c4ra15955a

---