The role of uniaxial strain in tailoring the interfacial properties of LaAlO₃/SrTiO₃ heterostructure

Abstract

The two-dimensional electron gas (2DEG) at the (LaO)⁺¹/(TiO₂)⁰ n-type interface in LaAlO₃/SrTiO₃ (LAO/STO) heterostructures (HS) opens up new opportunities in next-generation nanoelectronic devices because of its unique and tunable physical properties. In this respect, strain plays an important role in tailoring the 2DEG properties of STO-based HS systems. Our first-principles calculations reveal that a uniaxial strain along the [100]-direction of the STO substrate significantly affects the chemical bonding of LAO and STO near the interfacial region, which can further alter the interfacial electronic properties. We find that uniaxial tensile strain can considerably increase the interfacial charge carrier density, which is consistent with the recent experimental findings in [Moler et al., Nat. Mater., 2013, 12, 1091]. Our results also indicate that uniaxial compressive strain on STO can lead to higher interfacial charge carrier density and larger magnetic moments than uniaxial tensile strain, and further that the 2DEG in the compressively strained systems displays superior charge confinement in the c-direction. For the sake of comparison, the effects of ab-plane biaxial compressive and tensile strains applied on the STO substrate were also investigated. It is found that biaxial tensile strain improves the interfacial electronic properties and magnetic moments, while biaxial compressive strain shows the opposite effect.

---

1 Introduction

Heterostructures (HS) consisting of wide band gap perovskite oxide insulators have great potential to enhance the functionality of nanoelectronic devices due to their exceptional interfacial properties.^1–4 A classical example is the polar/non-polar LaAlO₃/SrTiO₃ (LAO/STO) epitaxial oxide HS. It exhibits many phenomena related to the interplay of strongly correlated electrons at TiO₂ terminated (TiO₂)⁰/(LaO)⁺¹ n-type interfaces, such as 2DEG with high charge carrier density (∼3.3 × 10¹³ cm⁻²) and mobility (∼10⁴ cm² V⁻¹ s⁻¹),⁵ coexistence of interfacial ferromagnetism and superconductivity,^6–10 and colossal magnetoresistance.^11,12 These unusual interfacial properties are interesting not only from a fundamental physics perspective but also for their exciting potential applications in nanoelectronic devices.^13–15 The typical explanation for the formation of such highly mobile 2DEGs at (TiO₂)⁰/(LaO)⁺¹ n-type interfaces is the so-called “polar catastrophe” mechanism.¹⁶ An electronic reconstruction occurs at the LAO/STO interface to compensate for the polar discontinuity by migrating electrons from the polar (LaO)⁺¹ layer of LAO to the adjacent non-polar (TiO₂)⁰ layers of the STO substrate. An insulator-to-metal transition occurs when the LAO film has a critical thickness of ≥4 unit cells.^17–19

Some experimental and theoretical efforts have been made to optimize the electron transport properties of the 2DEG in the LAO/STO HS.^20–23 On the one hand, the electronic properties of 2DEG have been adjusted by applying an external electric field,^11,17,24 enabling specific applications in 2DEG-based electronic devices.¹⁴ For example, both carrier concentration and the critical thickness of LAO for forming a 2DEG at the interface can be controlled with an external electric field.^2,24–26 On the other hand, strain engineering can also be used to tune 2DEG electron transport properties including charge carrier density and mobility. Some successful applications of strain engineering are found in traditional metal oxide semiconductor field effect transistors.^3,4 For example, strain can enhance the charge mobility in La-doped STO thin films by up to three-fold.²⁷ Likewise, by growing LAO/STO HS on different single crystal substrates, controllable ab-plane biaxial strains can be applied on the STO substrate. Such strains are capable of substantially influencing the interfacial charge carrier density and magnetic moments.^20,22

Very recently, Moler’s research team revealed that the STO substrate in the LAO/STO HS adopts a tetragonal domain structure near the interface, which significantly enhances the local conductivity.²¹ They found that the higher conductivity on the narrow domains of STO is due to a lengthened axis along either [100]_p or [010]_p, but that elongation along both directions yields no increase in conductivity. Previous experimental and computational studies, however, have indicated that applying a tensile biaxial strain improves the interfacial charge carrier density.^20,22 As demonstrated by this discrepancy, there must be some difference in the way uniaxial and biaxial strains influence 2DEG properties in the LAO/STO HS. Any strain-based optimization of these systems therefore demands a deeper understanding of precisely how uniaxial and biaxial strains influence the interfacial electronic properties.

In this work, we performed spin-polarized density functional theory calculations for the n-type (TiO₂)⁰/(LaO)⁺¹ interfaces of the (LAO)_4.5/(STO)_11.5 HS. The effects of both uniaxial compressive and tensile strains on the electron transport properties of 2DEG at this n-type interface were investigated in detail. For a complete comparison, the effects of biaxial strain were also studied. We show that both uniaxial compressive and tensile strains have a prominent effect on the interfacial Ti 3d orbital occupation, and hence significantly affect the interfacial charge carrier density and magnetic moments. The trend of interfacial charge carrier density and magnetic moment with respect to strain is explained in terms of buckling between cations and anions near the interfacial region due to the TiO₆ octahedral distortion.

2 Calculation methods

Spin-polarized calculations were performed by applying the Vienna Ab-initio Simulation Package.^28,29 The projected augmented wave (PAW) potentials were used for electron–ion interactions.^30,31 The generalized gradient approximation, parameterized by Perdew–Burke–Ernzerhof (PBE)³² plus the on-site Coulomb interaction approach, were used for the exchange-correlation potential with U = 5.8 eV and 7.5 eV for Ti 3d and La 4f orbitals, respectively. It is well established that the calculated U value of 5.8 eV for Ti 3d states from constrained density functional theory³³ is high enough to describe the correct Ti 3d states.^22,34,35 Similarly, U = 7.5 eV is a reasonable value for the strongly correlated La 4f electronic states.^15,36 A cutoff energy of 450 eV was used for the wave function expansion and a 10 × 10 × 1 k-space grid was found to be well-converged for self-consistent calculations. In order to resemble the experimental material growth process, all the atomic positions and lattice parameters along the z-axis of the strained and unstrained HS are fully relaxed by minimizing the atomic forces up to 0.02 eV Å⁻¹, while the cell parameters along the x- and y-axis are fixed in each system. Self-consistency was assumed for a total energy convergence of less than 10⁻⁵ eV. The accurate density of states (DOS) was calculated using a tetrahedron method with Blöchl corrections.³⁷ A supercell approach with periodic boundary conditions was used to model the LAO/STO HS, which contains two n-type (TiO₂)⁰/(LaO)⁺¹ symmetric interfaces. The experimental lattice constant of STO, 3.905 Å, was fixed in the ab-plane to construct the unstrained HS system and then varied corresponding to the applied strains.

3 Results and discussion

3.1 Unstrained heterostructure

To provide a frame of reference, we began by revisiting the electronic structure of the unstrained LAO/STO HS. We focused on the Ti 3d orbitals, as it is established that these orbitals are the primary contributors to the interfacial metallic states and form the 2DEG in the STO-based HS systems.²² We calculated the spin-polarized partial DOS projected on the Ti 3d orbitals for a fully relaxed n-type interface from three consecutive interfacial TiO₂ layers in the STO substrate. The 1st, 3rd, and 5th layers are defined as IF-I, IF-III, and IF-V, respectively. Fig. 1 clearly indicates that the Ti 3d orbitals from the 1st TiO₂ layer (IF-I) are mainly responsible for the metallic states, along with a small contribution from the 3rd layer (IF-III). The 5th layer (IF-V) of STO has nearly negligible contributions to the interfacial conductivity, and the layers further away from the interface show an insulating behaviour. Therefore, the metallic region extends up to 3 unit cells (9.6 Å thickness) into the STO substrate. The calculated interfacial magnetic moments of the Ti atoms of the IF-I/IF-III layers are 0.37 μ_B/0.11 μ_B, and the other layers away from the interface show no spin-polarization.

Fig. 1 Calculated spin-polarized partial DOS projected on the Ti 3d orbitals of an (LaO)⁺¹/(TiO₂)⁰ n-type interface in an unstrained LAO/STO HS near the interfacial region of STO. IF-I, IF-III, and IF-V represent the 1st, 3rd and 5th TiO₂ layers in STO, respectively. The positive and negative DOS curves indicate the spin-up and spin-down components, respectively. The Fermi level, E_F, is set as reference energy zero.

3.2 Uniaxial strain along the [100]-direction

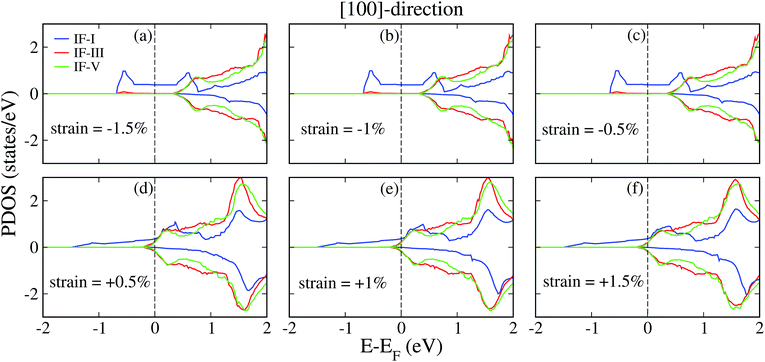
We next studied the effects of uniaxial compressive and tensile strains on the electronic properties of the 2DEG in the LAO/STO HS. The strained LAO/STO systems were modeled by adjusting the lattice parameters of the STO substrate in the [100]-direction. The experimental lattice parameter of STO, 3.905 Å, was used as a reference point and was then varied from −1.5% to +1.5%. The “−” and “+” signs indicate compressive and tensile strains, respectively. The strain effect in the [100]-direction on the electronic states near the interfacial region was analysed by plotting the partial DOS for −1.5% (a), −1% (b), −0.5% (c), +0.5% (d), +1% (e), and +1.5% (f) in Fig. 2. As we mentioned above, only the Ti 3d orbitals from the IF-I, IF-III, and IF-V TiO₂ layers were found to contribute to the interfacial metallicity (Fig. 1). Therefore, only these states were plotted in Fig. 2 for the various uniaxially strained systems.

Fig. 2 Calculated spin-polarized partial Ti 3d DOS at the (LaO)⁺¹/(TiO₂)⁰ n-type interfaces in the LAO/STO HS systems for −1.5% (a), −1% (b), −0.5% (c), +0.5% (d), +1% (e), and +1.5% (f) uniaxial strains along the [100]-direction on the STO substrate. The “−” and “+” signs indicate compressive and tensile strains, respectively.

Our results clearly indicate that all the strained systems form metallic states near the interfacial region, and that the interfacial conductivity mainly arises from the partial occupation of the Ti 3d orbitals in the IF-I TiO₂ layer. Interestingly, for all the compressively strained systems, the Ti 3d gap states on the IF-I layer shrink towards the conduction band and grow near the Fermi energy, thus increasing their orbital occupation (see Fig. 2a–c) with respect to tensile strain. One can also clearly see that the shape of the DOS in the compressively strained systems is very different than that of the tensile strained systems. The physical origin behind this phenomenon will be discussed later.

In contrast, the Ti 3d gap states from the IF-III and IF-V layers substantially recede into the conduction band and become unoccupied. This suggests that the 2DEG is tightly confined within a single unit cell of STO when the system is under compressive strain, because electron transfer from the polar (LaO)⁺¹ layer to the non-polar (TiO₂)⁰ IF-III and IF-V layers is strongly restricted. Hence, a superior charge confinement of the 2DEG along the c-direction is established for all the uniaxially compressively strained systems. On the other hand, when the LAO/STO HS undergoes uniaxial tensile strains, the Ti 3d gap states of the IF-I layer extend towards the valence band and their partial occupation increases (see Fig. 2d–f). However, a small but relevant number of charges are still transferred to the IF-III and IF-V layers, extending the 2DEG in the third dimension by ∼3 unit cells into the STO substrate. In conclusion, both compressive and tensile uniaxial strains increase the partial occupation of the Ti 3d orbitals in the first TiO₂ (IF-I) layer (Fig. 2) as compared to the unstrained system (Fig. 1), but superior charge confinement is found in the case of the compressively strained systems. In addition, it is noted that the lattice parameter along the z-axis of the HS model was fully relaxed in our simulation. As a result, the influence of the strain-induced c-lattice parameter variation on the electronic properties of the HS was also reflected by our calculations.

3.3 Biaxial strain along the [100] and [010]-directions

As a comparison to the [100]-oriented uniaxial strain cases detailed above, we now present the electronic structures of biaxially strained HS systems. The biaxially strained LAO/STO systems were modelled by tuning the lattice parameters of the STO substrate along both the [100] and [010]-directions. In other words, the strain applied along the x-axis was equal to that along the y-axis. As in the case of the uniaxially strained systems, we produced the partial DOS projected on the Ti 3d orbitals from the IF-I, IF-III, and IF-V TiO₂ layers for the LAO/STO HS systems with −1.5% (a), −0.5% (b), +0.5% (c), and +1.5% (d) biaxial strains, as shown in Fig. 3. The results demonstrate that all the biaxially strained systems retain metallic states at and near the interfacial region, as found in the case of uniaxially strained systems (Fig. 2). However, with respect to the unstrained system (Fig. 1), when the biaxial compressive strain is applied to the STO substrate, the partial occupation of the Ti 3d states of the IF-I TiO₂ layers is reduced and the states shrink towards the conduction band (see Fig. 3a and b). Yet, in the very same systems, the Ti 3d states in the IF-III and IF-V TiO₂ layers show the opposite response to the strain, whereby the occupation of the majority DOS increases with a concomitant decrease in the minority DOS. Thus the charge transfer from LAO to deeper TiO₂ layers in STO is magnified in compressively strained systems, leading to a 2DEG highly dispersed along the c-direction and a corresponding suppression of desirable quantum confinement effects.

Fig. 3 Calculated spin-polarized partial Ti 3d DOS at (LaO)⁺¹/(TiO₂)⁰ n-type interfaces in LAO/STO HS systems for −1.5% (a), −0.5% (b), +0.5% (c), and +1.5% (d) biaxial strains along the [100] and [010]-directions on the STO substrate.

When compared to biaxially compressively strained systems, the LAO/STO HS systems subjected to biaxial tensile strains show a precisely opposite trend. As tensile strain increases from +0.5% to +1.5%, the partial occupation of majority DOS for IF-I Ti atoms increases and states shift towards lower energies, see Fig. 3c and d as compared to compressively strained systems. On the other hand, the occupation of Ti 3d states in the IF-III and IF-V TiO₂ layers decreases and even disappears for the most tensile strained systems. Hence, the contribution to interfacial conductivity from IF-III and IF-V layers is nearly negligible. This strongly implies that the metallicity is primarily derived from the IF-I Ti 3d orbitals in these tensile strained systems. In particular, for the HS system with +1.5% strain (Fig. 3d), the Ti atoms on the IF-III and IF-V layers show nearly insulating behavior. This indicates that the 2DEG in this system exhibits a high degree of charge confinement, with an estimated depth of 3.9 Å along the c-direction. Hence, biaxial strain has a significant influence on the Ti 3d orbital occupation and spatial extension of the 2DEG along the c-axis. The compressive biaxial strains reduce the DOS for Ti 3d orbitals in the first TiO₂ (IF-I) layer around the Fermi energy as compared to the unstrained system (Fig. 1) and encourage charge transfer to deeper STO layers. In contrast, biaxial tensile strains lead to a strong confinement of 2DEG and a higher orbital occupation of Ti 3d orbitals at the IF-I layer.

3.4 Charge confinement along the c-axis

To illustrate the strain effects on the spatial extension of the electron gases along the c-axis, charge density plots projected on the bands forming the 2DEG for various uniaxially and biaxially strained systems are depicted in Fig. 4. Fig. 4a and b represent the systems with −1.5% uniaxial compressive and +1.5% uniaxial tensile strains along the [100]-direction, respectively. As a reference, the corresponding charge density for the unstrained HS is also shown in Fig. 4c. Similarly, the systems with −1.5% biaxial compressive and +1.5% biaxial tensile strains along the [100] and [010]-directions are illustrated in Fig. 4d and e, respectively. The results clearly indicate that when a −1.5% uniaxial compressive strain is applied on the STO substrate, the electrons transferred from the polar (LaO)⁺¹ layer to STO are totally confined within the (TiO₂)⁰ IF-I layer (Fig. 4a), forming a nearly ideal 2DEG. In the case of the +1.5% uniaxially tensile strained system, a small number of electrons are also transferred to the IF-III and IF-V TiO₂ layers, which extends the spatial thickness of the 2DEG along the c-axis (Fig. 4b). This spatial extension of the 2DEG in the third dimension dilutes the interfacial charge carrier density and weakens the quantum confinement effects. Biaxial strains seem to show an exactly opposite trend compared to uniaxial strain. In the −1.5% biaxially compressively strained HS, charge migrates to the deeper IF-V and even IF-VII (TiO₂)⁰ layers of STO (Fig. 4d), which expands the metallic region by ∼4.5 unit cells into the STO substrate along the c-axis. In the +1.5% biaxially tensile strained system (Fig. 4e), nearly all the electrons transferred from the polar (LaO)⁺¹ layer to STO are accumulated at the IF-I TiO₂ layer and a strong charge confinement to within only 1 unit cell of STO is found. These results confirm the calculated DOS shown in Fig. 2 and 3 for the uniaxially and biaxially strained systems, respectively, from a different perspective.

Fig. 4 Charge density plots projected on the bands forming the 2DEG in LAO/STO HS systems for −1.5% (a) and +1.5% (b) uniaxial strain along [100]-direction, 0% (unstrained) (c), −1.5% (d) and +1.5% (e) biaxial strain along [100] and [010]-directions on the STO substrate. The x, y, and z-axes are along the crystallographic a, b, and c-directions, respectively. The x-axis (a-direction) is pointing towards the observer.

In addition, it is noted that the shape of the charge density forming the 2DEG in the uniaxially compressively strained systems is vastly different from that in the unstrained and other strained systems. In the uniaxially compressively strained HS system, the charge density forming the 2DEG resides in the yz-plane, instead of the xy-plane as in other strained/unstrained systems (see Fig. 4a). This implies that the 2DEG comes from the partially occupied d_yz orbitals instead of the d_xy orbitals. This can also be seen from the DOS (Fig. 2a–c), which presents remarkably different shapes for uniaxially compressively strained systems compared to all the other systems considered in this study. According to crystal field theory, the Ti 3d orbitals in a regular octahedron are split into triply degenerate t_2g (d_xy, d_xz, and d_yz) and doubly degenerate e_g (d_3z²−r² and d_x²−y²) states. After the structural reconstruction, the distorted TiO₆ unit has a reduced symmetry, and the triply degenerate t_2g states are further split into non-degenerate d_xy, d_yz, and d_xz orbitals. To confirm this unusual behavior, we plotted the orbital-resolved DOS for −1.5% uniaxially compressively strained (Fig. 5a), unstrained (Fig. 5b), and −1.5% biaxially compressively strained (Fig. 5c) systems. From Fig. 5a, one can clearly see that in the case of the uniaxially strained system, only d_yz orbitals cross the Fermi level, and are thus singularly responsible for the 2DEG. The d_xy and d_xz orbitals remain unoccupied and stay at higher energies in the conduction band. In contrast, in the unstrained (Fig. 5b) and −1.5% biaxially compressively strained (Fig. 5c) systems, the metallicity mainly comes from d_xy orbitals. This peculiar electronic behavior in the uniaxially compressively strained system can be attributed to a different TiO₆ octahedral distortion as compared to other systems (discussed later).

Fig. 5 Orbital-resolved partial DOS of the Ti 3d orbitals from IF-I TiO₂ layers at (LaO)⁺¹/(TiO₂)⁰ n-type interfaces in LAO/STO HS systems for −1.5% (a) uniaxial compressive strain along the [100]-direction, 0% (unstrained) (b) and −1.5% (c) biaxial compressive strain along the [100] and [010]-directions on the STO substrate.

3.5 Interfacial charge carrier density and magnetic moment

For a qualitative comparison of these various strained systems, we calculated their interfacial (IF-I) charge carrier densities and magnetic moments, as shown in Fig. 6. To do this, we calculated the occupation number of the Ti 3d orbitals of the IF-I TiO₂ layer by integrating the DOS. The estimated values are 0.35/0.16, 0.35/0.16, 0.35/0.18, 0.285/0.285, 0.29/0.28, 0.30/0.30, and 0.31/0.32 for −1.5%, −1%, −0.5%, 0%, +0.5%, +1%, and +1.5% strains in uniaxially/biaxially strained systems, respectively. In both uniaxially compressive and tensile strained systems, orbital occupation is higher than that of the unstrained system (0.27e). However, uniaxial compressive strain is much more effective at increasing the d-orbital occupation as compared to uniaxial tensile strain. In contrast, the biaxially strained systems show a different trend. Lower and higher occupation is observed for the most compressive (−1.5%) and tensile (+1.5%) strained systems, respectively. Hence, in the biaxially strained systems, Ti 3d orbital occupation tends to increase when a transition from compressive to tensile strain occurs. The corresponding charge carrier densities for IF-I Ti 3d orbitals are exhibited in Fig. 6a for uniaxially and biaxially strained systems, which show significant interdependence with respect to lattice strain. These results indicate that a higher interfacial charge carrier density can be obtained in the uniaxially compressively (−1.5%) strained system, with lower values in the biaxially compressively strained (−1.5%) systems. In contrast, both the uniaxially and biaxially tensile strained systems show almost similar charge carrier densities, with an increase proportional to the applied tensile strain.

Fig. 6 Calculated interfacial (a) charge carrier densities and (b) magnetic moments of the Ti 3d orbitals from IF-I TiO₂ layers at (LaO)⁺¹/(TiO₂)⁰ n-type interfaces in LAO/STO HS systems with respect to strain for uniaxial strain along the [100]-direction and biaxial strain along the [100] and [010]-directions on the STO substrate.

We next examined the strain-induced variation of the magnetic moments in these HS systems. Due to charge transfer from the polar (LaO)⁺¹ layer to non-polar (TiO₂)⁰ layers, the Ti 3d orbitals are partially occupied, which results in magnetic moments on the Ti atoms. The calculated magnetic moments of the Ti atoms in the IF-I layer are plotted in Fig. 6b for both uniaxially and biaxially strained systems. The interfacial magnetic moments vary with strain in much the same way as the charge carrier density. The systems with −1.5% uniaxial and biaxial strain have the largest and smallest magnetic moments at the interfacial TiO₂ layer, respectively. The deeper TiO₂ layers in the uniaxially strained system do not exhibit any spin-polarization (Fig. 2a), while in the biaxially strained system, the Ti atoms in the IF-III/IF-V layers remain spin-polarized with magnetic moments of about 0.09 μ_B/0.07 μ_B (Fig. 3a). This is due to a smaller amount of charge transfer to the deeper layers of STO in the case of biaxial compressive strain. For uniaxially and biaxially tensile strained systems, the changing trend of the magnetic moments shows a similar behavior to that of the interfacial charge carrier density (see Fig. 6a).

Our calculations show that when uniaxial strain is adjusted from 0% to +1.5%, the charge carrier density and magnetic moment increase slightly. These results are in good agreement with recent experimental findings by Moler et al.²¹ They observed that the LAO/STO system exhibits an enhancement in local conductivity when strain is induced due to the tetragonal domain structure of the STO substrate with a lengthened axis along the [100] or [010]-directions near the interfacial region. However, here we also want to mention that a higher charge carrier density can be found in the uniaxially compressively strained systems than in the uniaxially tensile strained HS. Furthermore, in the uniaxially compressively strained systems, the metallic Ti 3d states forming the 2DEG come from the partially occupied d_yz orbitals instead of the d_xy orbitals (as observed for all the remaining systems). In biaxially strained systems, by contrast, the charge density and magnetic moment increase when strain is applied in the ab-plane from −1.5% to +1.5%. Hence, our results suggest that interfacial charge carrier density and magnetism could be significantly optimized by applying an appropriate strain on the STO substrate.

3.6 Structural distortion

To understand the different strain effects on the electronic properties of the LAO/STO system, we plotted the locally distorted TiO₆ octahedra along with the calculated three-dimensional charge density projected on the bands forming the 2DEG for different strained systems in Fig. 7. The distorted TiO₆ octahedra of the uniaxially compressive (−1.5%) and tensile (+1.5%) strained systems are depicted in Fig. 7a and b, while those of the biaxially compressive (−1.5%) and tensile (+1.5%) strained systems are shown in Fig. 7d and e. The distorted TiO₆ octahedron in the unstrained system is shown in Fig. 7c for comparison. It is found that the Ti–O bond length is elongated from 1.93 Å to 1.98 Å in the ab-plane when moving from biaxially compressive to tensile strained systems (see Fig. 7d and e). Due to the elongated Ti–O bond length in the tensile strained (+1.5%) system (Fig. 7e), Ti d_xy orbital electrons can be highly confined to the interfacial TiO₂ layer. Therefore, electron transfer to deeper STO layers is strongly restricted, as shown in Fig. 4e. In contrast, when a compressive (−1.5%) strain is applied on the STO substrate, the Ti–O bond length in the ab-plane decreases (Fig. 7d), and Ti d_xy orbitals on the interfacial layer cannot hold all the electrons, hence the remaining electrons will be transferred to deeper IF-III, IF-V, and even IF-VII STO layers compared to the unstrained system (see Fig. 4d).

Fig. 7 Locally distorted TiO₆ octahedra and the calculated three-dimensional charge density projected on the bands forming the 2DEG at the interfacial plane in LAO/STO HS systems for −1.5% (a) and +1.5% (b) uniaxial strains along the [100]-direction, 0% (unstrained) (c), and −1.5% (d) and +1.5% (d) biaxial strains along the [100] and [010]-directions on the STO substrate. The x, y, and z-axes are along the crystallographic a, b, and c-directions, respectively.

The variation in the Ti–O bond length in uniaxially compressively strained systems, however, differs markedly from that in biaxially strained systems. Along the x-axis, the Ti–O bond length decreases to 1.93 Å for compressively strained systems (Fig. 7a). However, along the y-axis, the bond length remains nearly unchanged from that of the unstrained system, ∼1.96 Å (not shown in Fig. 7a). Along the z-axis (perpendicular to the interfacial plane), compressive strains cause the Ti–O bond length to extend on both sides of the interfacial plane as compared to biaxially strained systems (see Fig. 7a and d). In conclusion, in the uniaxially compressively strained system, the Ti–O bond length along the x-axis is smaller than that along either the y or z-axis. In fact, the bond length of the two Ti–O bonds along the z-axis in the interfacial layer are even elongated relative to the systems subjected to biaxial compressive strain. Therefore, the elongated Ti–O bond length in the yz-plane leads to partially occupied electronic states in the Ti 3d_yz orbitals. In summary, this peculiar relaxation pattern could be a possible explanation for why, in uniaxially compressively strained systems, nearly all the electrons transferred from (LaO)⁺¹ reside in the interfacial plane and the 2DEG is composed of d_yz instead of d_xy orbitals. For the uniaxially tensile (+1.5%) strained system, the Ti–O bond length along the x-axis increases to 1.99 Å and shows a similar trend along the z-axis with that of the biaxially tensile (+1.5%) strained system (see Fig. 7b and e), while the Ti–O bond length along y-axis has a comparable value (1.96 Å) to that found in the unstrained system. Hence, the metallic states forming the 2DEG are still contributed by the Ti d_xy orbitals.

4 Conclusion

In summary, the electronic and magnetic properties of (TiO₂)⁰/(LaO)⁺¹ n-type interfaces in the unstrained and strained (uniaxial and biaxial) LAO/STO HS systems were studied using spin-polarized density functional theory electronic structure calculations. It is found that the charge carrier density and magnetic moment localized on the interfacial plane of 2DEG systems strongly depend on the type and magnitude of the lattice strain exerted on the STO substrate. Our results indicate that the Ti–O bond length has a substantial effect on the interfacial charge carrier density and the magnetic moment. In the uniaxially tensile strained system, the longer Ti–O bond length along the a-axis leads to higher interfacial charge carrier density and magnetic moment. In the uniaxially compressively strained system, the compressive strain along the [100]-direction leads to the longest Ti–O bonds along the c-axis nearest to LAO compared to those in all the other strained systems. This structural character determines that the metallic states forming the 2DEG come from the Ti 3d_yz orbitals instead of the Ti 3d_xy orbitals, which further results in the strongest charge confinement effects with the highest interfacial charge carrier densities and magnetic moments. In addition, our calculations suggest that a superior electron confinement at the interfacial layer can also be realized in the biaxially tensile strained system.

Acknowledgements

The authors thank Camille Bernal for useful discussions. This work is partially supported by ONR (N000141510030). KY acknowledges support from start-up funds from the University of California, San Diego.

References

1. J. Mannhart and D. G. Schlom, Science, 2010, 327, 1607–1611.
2. T. Yajima, Y. Hikita and H. Y. Hwang, Nat. Mater., 2011, 10, 198201.
3. H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Nat. Mater., 2012, 11, 103113.
4. Z. G. Sheng, M. Nakamura, W. Koshibae, T. Makino, Y. Tokura and M. Kawasaki, Nat. Commun., 2014, 5, 4584.
5. A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426.
6. L. Li, C. Richter, J. Mannhart and R. C. Ashoori, Nat. Phys., 2011, 7, 762.
7. J. A. Bert, B. Kalisky, C. Bell, M. Kim, Y. Hikita, H. Y. Hwang and K. A. Moler, Nat. Phys., 2011, 7, 767–771.
8. D. A. Dikin, M. Mehta, C. W. Bark, C. M. Folkman, C. B. Eom and V. Chandrasekhar, Phys. Rev. Lett., 2011, 107, 056802.
9. B. Kalisky, J. A. Bert, B. B. Klopfer, C. Bell, H. K. Sato, M. Hosoda, Y. Hikita, H. Y. Hwang and K. A. Moler, Nat. Commun., 2012, 3, 922.
10. J. S. Lee, Y. W. Xie, H. K. Sato, C. Bell, Y. Hikita, H. Y. Hwang and C. C. Kao, Nat. Mater., 2013, 12, 703–706.
11. A. Brinkman, M. Huijben, M. van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. van der Wiel, G. Rijnders, D. H. A. Blank and H. Hilgenkamp, Nat. Mater., 2007, 6, 493–496.
12. G. Herranz, M. Basletić, M. Bibes, C. Carrétéro, E. Tafra, E. Jacquet, K. Bouzehouane, C. Deranlot, A. Hamzic, J.-M. Broto, A. Barthélémy and A. Fert, Phys. Rev. Lett., 2007, 98, 216803.
13. C. Cen, S. Thiel, G. Hammerl, C. W. Schneider, K. E. Andersen, C. S. Hellberg, J. Mannhart and J. Levy, Nat. Mater., 2008, 7, 298–302.
14. C. Cen, S. Thiel, J. Mannhart and J. Levy, Science, 2009, 323, 1026–1030.
15. R. Arras, V. G. Ruiz, W. E. Pickett and R. Pentcheva, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125404.
16. N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204–209.
17. S. Thiel, G. Hammerl, A. Schmehl, C. W. Schneider and J. Mannhart, Science, 2006, 313, 1942–1945.
18. Z. Ristic, R. Di Capua, F. Chiarella, G. M. De Luca, I. Maggio-Aprile, M. Radovic and M. Salluzzo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045127.
19. T. C. Asmara, A. Annadi, I. Santoso, P. K. Gogoi, A. Kotlov, H. M. Omer, M. Motapothula, M. B. H. Breese, M. Rübhausen, T. Venkatesan, Ariando and A. Rusydi, Nat. Commun., 2014, 5, 3663.
20. C. W. Bark, D. A. Felker, Y. Wang, Y. Zhang, H. W. Jang, C. M. Folkman, J. W. Park, S. H. Baek, H. Zhou, D. D. Fong, X. Q. Pan, E. Y. Tsymbal, M. S. Rzchowski and C. B. Eom, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4720–4724.
21. B. Kalisky, E. M. Spanton, H. Noad, J. R. Kirtley, K. C. Nowack, C. Bell, H. K. Sato, M. Hosoda, Y. Xie, Y. Hikita, C. Woltmann, G. Pfanzelt, R. Jany, C. Richter, H. Y. Hwang, J. Mannhart and K. A. Moler, Nat. Mater., 2013, 12, 1091–1095.
22. S. Nazir, M. Behtash and K. Yang, Appl. Phys. Lett., 2014, 105, 141602–141605.
23. S. Nazir and K. Yang, ACS Appl. Mater. Interfaces, 2014, 6, 22351–22358.
24. A. Rastogi, A. K. Kushwaha, T. Shiyani, A. Gangawar and R. C. Budhani, Adv. Mater., 2010, 22, 4448–4451.
25. A. D. Caviglia, S. Gariglio, N. Reyren, D. Jaccard, T. Schneider, M. Gabay, S. Thiel, G. Hammerl, J. Mannhart and J. M. Triscone, Nature, 2008, 456, 624–627.
26. N. Reyren, S. Thiel, A. D. Caviglia, L. F. Kourkoutis, G. Hammer, C. Richter, C. W. Schneider, T. Kopp, A. S. Rüetschi, D. Jaccard, M. Gabay, D. A. Muller, J. M. Triscone and J. Mannhart, Science, 2007, 317, 1196–1199.
27. B. Jalan, S. J. Allen, G. E. Beltz, P. Moetakef and S. Stemmer, Appl. Phys. Lett., 2011, 98, 132102–132104.
28. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
29. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
30. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
34. K. Yang, Y. Dai, B. Huang and Y. P. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 033202.
35. K. Yang, Y. Dai, B. Huang and Y. P. Feng, J. Phys. D: Appl. Phys., 2014, 47, 275101.
36. R. Pentcheva and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205106.
37. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.

---