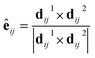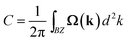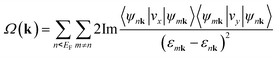Prediction of quantum anomalous Hall effect on graphene nanomesh

Abstract

A quantum anomalous Hall effect (QAHE) has been realized in the Cr-doped magnetic topological insulator at an extremely low temperature (∼30 mK). From first-principles, we predict that QAHE can also be achieved in a well-designed graphene nanomesh without the requirement of transition metal doping. The ferromagnetic ordering arises mainly from the in-plane p_xy orbitals, leading to a Curie temperature of 830 K. The bulk band gap due to the intrinsic spin–orbital coupling (SOC) of the p_xy orbitals is about 3.7 meV, corresponding to an operating temperature of 43 K. This work reveals a viable approach for realizing QAHE in metal-free graphene nanostructures.

---

Introduction

The quantum anomalous Hall effect (QAHE) is a topological nontrivial phase characterized by a finite Chern number and helical edge states within the bulk band gap. Without an external magnetic field, internal magnetization breaks time-reversal symmetry and spin–orbit coupling (SOC) opens a SOC-gap, giving rise to a quantized anomalous Hall conductivity. The Hall conductivity σ_xy develops plateaus at values (Chern number) quantized in unit of e²/h. The helical edge states are robust against backscattering and thus promising for low power consumption device applications.

Haldane first proposed a honeycomb-net model (known as Haldane model) for achieving QAHE. He demonstrated theoretically that the break of time-reversal invariance does not necessarily require external magnetic fields, but could occur as a consequence of magnetic ordering in a quasi-two-dimensional lattice.^1,2 The internal ferromagnetic (FM) ordering splits the spin-degenerated bands of topological insulators (TIs), leading to time-reversal symmetry-breaking. Magnetic topological insulators (TIs) are therefore expected to be promising for achieving QAHE.^3–7 In order to induce stable FM ordering, heavy transition metals are included in these systems, such as mercury-based quantum wells,⁸ topological insulator thin films containing heavy elements,^9,10 graphene^11–13 and silicene^14,15 based systems, and kagome lattice^16,17 systems. However, due to the difficulty in controlling magnetization and SOC, the QAHE has not been observed experimentally until very recently, when it was finally realized in a Cr-doped (Bi, Sb)₂Te₃ topological insulator at extremely low temperature (∼30 mK).¹⁸

Meanwhile, increasing attention has been paid to searching for metal-free topological insulators, since the first prediction on the quantum spin Hall (QSH) states of graphene.¹⁹ However, the SOC in graphene is extremely weak, leading to a unobservably small topologically nontrivial band gap, which limits the operating regime to unrealistically low temperatures. Several two-dimensional (2D) materials beyond graphene, such as silicene, germanene,²⁰ silicon carbide,²¹ graphyne,²² carbon nitride,²³ have been proposed as candidates for achieving QSH effect at an experimentally accessible temperature. These works enrich the database of 2D TIs and offer additional candidate materials for achieving QAHE by inducing stable FM ordering. Notably, theoretical works have showed that other than transition metal atoms, nitrogen atom can induce stable FM ordering in semiconductors, such as graphitic carbon nitrides^24–26 and silicon carbide.²⁷

In this work, based on first-principles calculations, we propose a nitrogen-doped graphene kagome nanomesh as a promising metal-free magnetic topological insulator, which can be used to realize QAHE at high temperature. Combined with a Monte Carlo (MC) simulation and anomalous Hall conductivity calculation, we demonstrate that this nanomesh has stable FM ordering with a Curie temperature of 830 K and a topologically nontrivial band gap of 3.7 meV (∼43 K) characterized by a Chern number of −1. The stable FM and relatively strong SOC are both related to the in-plane p_xy atomic orbitals rather than the p_z orbital. We also propose a single orbital tight binding (TB) model on an extended ruby lattice (named as extended ruby model) to reproduce the exotic properties of the nanomesh. The high Curie temperature and moderate SOC gap indicate the feasibility of the QAHE in the metal-free magnetic TI at experimentally accessible temperature.

Method and computational details

Our first principles calculations are performed in the framework of density-functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP).²⁸ The electron–electron interactions are treated within a generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE) for the exchange-correlation functional.²⁹ The electron–ion interaction is described by projector-augmented-wave (PAW) potentials. The electron wave functions are expanded using the plane-waves with the energy cutoff of 500 eV. Self-consistent solution of the Kohn–Sham equation is carried out with the convergence of 10⁻⁸. The supercells are repeated periodically on the x–y plane while a vacuum region of about 15 Å is applied along the z-direction to avoid mirror interaction between neighboring images. A symmetry reduced 13 × 13 × 1 Monkhorst-Pack sampling is used for the Brillouin zone (BZ) integration. Structural optimizations are performed using a conjugate gradient (CG) method until the remanent force on each atom is less than 0.002 eV Å⁻¹. Electron spin-polarization is involved in all calculations. The phonon spectra are calculated using a finite displacement method, as implemented in the phonon code^30,31 combined with the VASP code. The anomalous Hall conductivity was calculated using the Kubo formula based on the maximally localized Wannier functions.³²

Result and discussion

The optimized nitrogen-doped graphene kagome nanomesh is shown in Fig. 1a. It can be regarded as a porous graphene monolayer with the marginal carbon (C) atoms around the pores being substituted by nitrogen (N) atoms. We chose N dopant here considering that N have been widely used for chemical doping of carbon materials due to a comparable atomic size and five valence electrons for bonding with carbon atoms.³³ Meanwhile, N-doping of graphene was highly effective in modulating its band gap to achieve new properties for device applications.³⁴ It is clearly that the planar configuration and six-fold rotational symmetry of the nanomesh are both preserved, displaying characteristics of a structurally perfect kagome lattice. The equilibrium lattice constant is found to be 11.77 Å with an angle of 60° or 120° between the primitive vectors from present calculations. A vibrational analysis of phonon spectrum calculated from first-principles confirms the stability of the hypothetic nanomesh, because no modes with imaginary frequencies are found in the phonon spectrum along the highly symmetric points in BZ as shown in Fig. 1b.

Fig. 1 (a) Schematic representation and (b) phonon spectrums of the nitrogen-doped graphene kagome nanomesh.

Certainly, the experimental realization of the nanomesh remains challenging for chemists, though it is kinetically stable. Both unified pores in graphene and exactly N-doping are difficult to control in experiments. However, the recent refinements in the techniques of fabricating porous graphene nanomeshs (GNMs)^35–38 offer potential pathways to synthesizing a GNM with well-ordered, appropriately-sized pores. Meanwhile, started from the functionalization of graphene with nitrogen achieved by Wang et al.,³⁹ abundant strategies to prepare N-doped graphene has been reported in controlled ways.^40–43 The doping nitrogen tend to siting at the edge of pores^44,45 provides a promising prospect to controllable synthesis of the nanomesh proposed in Fig. 1a. Notably, the above top-down strategy involves the generation of well-ordered pores in graphene sheets, which may be limited by the quality of GNMs. Bottom-up approaches refer to the construction of nanomesh from small organic precursor molecules through catalytic or thermal treatment. The power of this synthetic approach lies in the fact that it is possible to design molecular precursors leading to uniquely defined structures. This approach was successfully applied to construct a two-dimensional framework from building blocks created via the trimerizaton of terephthalonitrile.⁴⁶ Hence, the N-doped graphene kagome nanomesh may also be synthesized by the controlled bottom-up approach with appropriate precursor monomers, such as N-doped graphene quantum dots (N-GQDs)⁴⁷ and melem pre-treated with absolute ethanol.^48–50

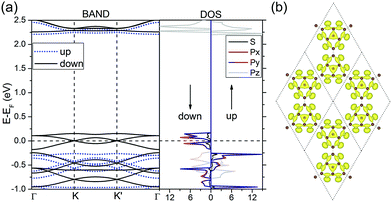
To understand the electronic properties of nanomesh, we performed electronic band structure calculations. Self-consistent calculations without SOC gave a stable spin-polarized state with a magnetic moment of 2.0 μ_B in one unit cell (containing a C₁₄N₁₂ formula). The spin-resolved band structures are plotted in Fig. 2a along the highly-symmetric points (K and K′) in BZ. We can clearly see the characteristics of kagome-like bands consisting of one flat band above two Dirac bands. Notably, because of the magnetization, the spin degeneracy of the kagome-like bands is lifted with spin-down channel being well separated from other bands and the Fermi level crossing the Dirac point exactly (a spin-gapless semiconductor). The Dirac points of the two spin channels remain touching at the K or K′ points in BZ, but with a split of about 0.42 eV. The features can be seen more clearly from the orbital-resolved electron density of states (DOS) shown in the right panel of Fig. 2a. Meanwhile, the DOS demonstrates that the local magnetic moments come mainly from the p_x and p_y electrons and minor from the s electrons, rather than the p_z electrons. This feature is further confirmed by the isosurfaces of Kohn–Sham wave functions of the three spin-polarized kagome-like bands. The shapes of the isosurfaces shown in Fig. 2b display clearly characteristics of hybridized p_xy orbitals, which are expected to have stronger SOC effect than p_z orbital.^23,51

Fig. 2 (a) Spin-resolved band lines (without SOC) and orbital-resolved electron density of states of the nanomesh. (b) The isosurfaces of Kohn–Sham wave functions of the three bands in proximity of the Fermi level with the isosurface value of 0.004 Å⁻³.

Since the nanomesh is magnetic, it is of interest to study the preferred magnetic coupling between local magnetic moments. We first carefully studied the magnetic interaction in one unit cell and found that there is no stable solution with an antiferromagnetic configuration (AFM), and the ferromagnetic (FM) ordering is the ground state which is more stable than the nonmagnetic (NM) state by about 145.6 meV. This result can be explained from the perspective of the energy levels of the isolated molecules (see Fig. 3a) constituting the nanomesh. After structural relaxation, self-consistent calculations demonstrated that the molecule favors a spin-polarized ground state. For the three energy levels nearest to the Fermi level, the spin-up branch is fully occupied and the spin-down branch is only partially (2/3) occupied, producing a net magnetic moment of 1.0 μ_B (see Fig. 3a). These partially-occupied states can act as acceptor levels and mediate a virtual hopping between adjacent magnetic moments for the FM arrangement as shown in Fig. 3b, leading to a stable FM state.⁵²

Fig. 3 Schematic diagrams of spin-resolved energy levels exchange mechanisms for (a) isolated molecule and (b) molecular dimer cutting from the nanomesh with the corner carbon passivated by hydrogen. (c) The exchange mechanisms for the graphene nanomesh. (d) FM and AFM orderings of the graphene nanomesh. The direction of magnetic moments are represented by dot or cross in circle. (e) Temperature-dependent average energy and magnetic moments per unit cell.

Consequently, we adopted large-size supercells containing four primitive cells (donated as 2 × 2) to further confirm the magnetic coupling and estimate Curie temperature. Starting from different initial spin arrangements of the local magnetic moments of 2.0 μ_B, self-consistent calculations lead to two types of magnetic orderings, FM and AFM, as shown in Fig. 3d, respectively. The AFM states can be seen as an antiferromagnetic combination of collinear ferromagnetic configuration. We found that the AFM phase is less stable than the FM phase by about 426.3 meV per 2 × 2 cell. Hence, The nearest-neighbor exchange parameterJ₀ of the local magnetic moments can be evaluated using the Ising model without an external field, , where m̂_i and m̂_j are the local magnetic moments at the nearest-neighbor sites i and j. By comparing the DFT total energies of FM and AFM phase, the value of J₀ is extracted as 6.66 meV using the following formula: J₀ = ΔE/16m². We then estimated the Curie temperature (T_C) from a Monte Carlo (MC) simulation within the Ising Hamiltonian. Starting from the initial spin arrangements of FM (see Fig. 3d) in a 100 × 100 supercell containing 10⁴ local magnetic moments, we got the variation of average energy and magnetic moment as a function of temperature shown in Fig. 3e. It can be seen that the average energy gradually rises with the increase of temperature and the magnetic moment per unit cell rapidly falls to 0.0 μ_B at the temperature of T_C = 830 K, indicating the system undergoes a transition from FM to paramagnetic (PM) at this temperature. Although this MC simulation only gives a rough estimation of the Curie temperature, it is consistent with the high stability of the FM state superior to the AFM state. This is related to the large split between the two spin channels in the region near the Fermi level. The partially-occupied acceptor levels allow virtual hopping for the FM arrangement,²⁷ as shown in Fig. 3c, whereas the AFM arrangement is highly energetically disadvantageous.

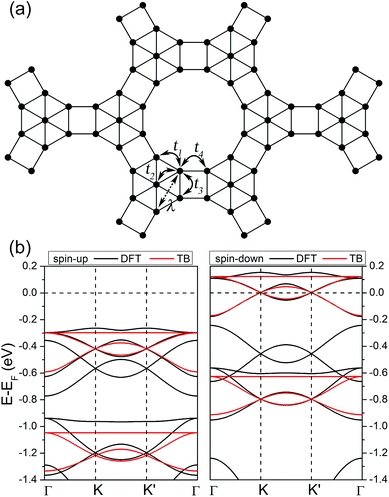
We now go back to the band structures of the ferromagnetic N-doped graphene kagome nanomesh and investigate its topological properties. In addition to the atomic orbitals discussed earlier in this article, the isosurfaces of Kohn–Sham wave functions shown in Fig. 2b also suggests the kagome-like bands come mainly from the marginal N and center C atoms and minor from the remaining atoms. Based on the features, we adopted a single-orbital tight-binding (TB) model with an exchange field and onsite energy to reproduce the spin-polarized kagome-like bands. In this model, we only consider the nearest-neighbor (NN) hopping between marginal N and center C atoms, leading to an extended ruby lattice, as shown in Fig. 4a. According to this approximation, the Hamiltonian is expressed as follows:

here, c⁺_iα and c_iα are creation and annihilation operators, respectively, for an electron with spin α on site i. ε_on is onsite energy for both spin up and down channels. t_ij is the distance-dependent nearest-neighbor hopping parameters labeled t₁, t₂, t₃, and t₄ in Fig. 4a. In addition to the nearest-neighbor hopping term (the first term), the exchange field with M is involved (the second term). Diagonalizing the above Hamiltonian in reciprocal space, we obtain its band structures, as shown in Fig. 4b. The band structures reproduce well the spin-polarized kagome-like bands given by DFT calculations with the optimal parameters of ε_on = 1.7032 eV, t₁ = −0.180 eV,t₂ = −0.100 eV, t₃ = −2.250 eV, t₄ = −0.375 eV, and M = −0.21 eV, respectively. This implies that the exchange field causes the spin-polarized kagome-like bands and adjusts the Dirac points to the Fermi level.

Fig. 4 (a) Schematic representation of the extended ruby lattice. t₁, t₂, t₃, and t₄ represent the nearest-neighbor hopping parameters and λ is the next-nearest-neighbor intrinsic SOC parameter. (b) A comparison between the band structures calculated from first-principles (DFT) and the extended ruby model.

Next, we investigated the SOC effects. The band structures with SOC are almost identical to those without SOC (see Fig. 2a), except a SOC band gap of 3.7 meV at K or K′ points in proximity of the Fermi level, which can be seen clearly from the magnified bands in Fig. 5a. The SOC band gap can be well described using the above extended ruby model combined with spin–orbital interaction, and the TB Hamiltonian is written as:

Fig. 5 (a) Enlarged view of the kagome-like bands with SOC nearest to the Fermi level calculated from DFT, TB, and Wannier90 (left panel), and anomalous Hall conductivity calculated from the maximally localized Wannier functions (right panel). (b) The 2D distribution of the Berry curvature for the Dirac bands (I and II) obtained from TB in the momentum space. The dashed lines mark the first Brillouin zone.

The spin–orbital interaction is defined as spin-dependent second-nearest-neighbor hopping. λ is spin–orbital coupling strength shown in Fig. 4a and s is the spin Pauli matrix. The unit vector ê_ij is defined as:

where d_ij¹ and d_ij² are bond vectors along the two bonds that the electron traverses when going from atom j to i. According to this definition, s·ê_ij = ±s^z. We note that this intrinsic SOC term forbids mixing of spin-up and spin-down channels due to the special nature of the 2D extended ruby model. Based on the above Hamiltonian with λ = 0.0013 eV, the two Dirac bands are well reproduced as shown in Fig. 5a. This implies that the SOC gap of the Dirac bands in the N-doped graphene kagome nanomesh is opened due to intrinsic SOC.

The nontrivial topology of the SOC gaps can be confirmed by the Chern number (C) calculated from the k-space integral of Barry curvature (Ω(k)) of all the states below the Fermi level using the Kubo formula:

with
where ψ_nk is the spinor Bloch wave function of band n with the corresponding eigenenergy ε_nk and v_i is the ith Cartesian component of the velocity operator. The right panel of Fig. 5a shows the calculated anomalous Hall conductivity as a function of energy based on maximally localized Wannier functions, which develops plateaus at the value of −1.0e²/h within the energy window of SOC gaps. This implies that the N-doped graphene kagome nanomesh has a topologically nontrivial state at the Fermi level with a Chern number of C = −1. The well match between Wannier and DFT bands shown in the left pannel of Fig. 5a ensures the accuracy of the anomalous Hall conductivity. Based on the extended ruby model, we also calculated the distribution of Berry curvatures for the lowest conduction band (I) and highest valence band (II) around the Fermi level, respectively, and plotted tham in Fig. 5b. It is obvious that the Berry curvature of the two Dirac bands resides mainly around the K or K′ point in BZ. More importantly, the nontrivial SOC gap in the graphene nanomesh is well separated from other bands and thus implementable in achieving the QAHE at low temperature (∼43 K).⁵³

Conclusions

Using first-principles calculations combined with a tight-binding model, we propose a nitrogen-doped graphene kagome nanomesh which has electronic structures characterized by kagome-like bands composing of one flat band above two Dirac bands. A moderate band gap of 3.7 meV is opened due to intrinsic SOC at the Fermi level. Anomalous Hall conductivity and Berry curvatures calculations show that the graphene nanomesh is a two-dimensional magnetic toplogical insulator characterized by a Chern number of −1, which may be implementable for achieving the QAHE at low temperature (∼43 K). The physical origins of QAHE are the relatively strong SOC effect and stable FM state provided by p_xy atomic orbitals. These features can be described by using an extended ruby model. This work suggests a promising approach to search for metal-free magnetic TIs for realizing QAHE at high temperatures.

Acknowledgements

This work is supported by the National Basic Research Program of China (no. 2012CB932302), the National Natural Science Foundation of China (nos 91221101 and 21433006), the 111 project (no. B13209), the Taishan Scholar Program of Shandong, and the National Super Computing Centre in Jinan.

References

1. F. D. M. Haldane, Phys. Rev. Lett., 1988, 61, 2015–2018.
2. M. Onoda and N. Nagaosa, Phys. Rev. Lett., 2003, 90, 206601.
3. H. Zhang, C. Lazo, S. Blügel, S. Heinze and Y. Mokrousov, Phys. Rev. Lett., 2012, 108, 056802.
4. H. Zhang, F. Freimuth, G. Bihlmayer, M. Ležaić, S. Blügel and Y. Mokrousov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205132.
5. Z. F. Wang, Z. Liu and F. Liu, Phys. Rev. Lett., 2013, 110, 196801.
6. Y. Zhang and J. Shi, Phys. Rev. Lett., 2014, 113, 016801.
7. R. Yu, W. Zhang, H. J. Zhang, S. C. Zhang, X. Dai and Z. Fang, Science, 2010, 329, 61–64.
8. C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Phys. Rev. Lett., 2008, 101, 146802.
9. K. Garrity and D. Vanderbilt, Phys. Rev. Lett., 2013, 110, 116802.
10. Y. Ma, Y. Dai, X. Li, Q. Sun and B. Huang, Carbon, 2014, 73, 382–388.
11. W.-K. Tse, Z. Qiao, Y. Yao, A. H. MacDonald and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155447.
12. Z. Qiao, W. Ren, H. Chen, L. Bellaiche, Z. Zhang, A. H. MacDonald and Q. Niu, Phys. Rev. Lett., 2014, 112, 116404.
13. Z. Qiao, S. Yang, W. Feng, W.-K. Tse, J. Ding, Y. Yao, J. Wang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161414.
14. H. Pan, Z. Li, C.-C. Liu, G. Zhu, Z. Qiao and Y. Yao, Phys. Rev. Lett., 2014, 112, 106802.
15. X.-L. Zhang, L.-F. Liu and W.-M. Liu, Sci. Rep., 2013, 3, 2908.
16. M. Zhao, A. Wang and X. Zhang, Nanoscale, 2013, 5, 10404–10408.
17. Z. Y. Zhang, J Phys Condens Matter, 2011, 23, 365801.
18. C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L. L. Wang, Z. Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S. C. Zhang, K. He, Y. Wang, L. Lu, X. C. Ma and Q. K. Xue, Science, 2013, 340, 167–170.
19. C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 146802.
20. C.-C. Liu, W. Feng and Y. Yao, Phys. Rev. Lett., 2011, 107, 076802.
21. M. Zhao and R. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195427.
22. M. Zhao, W. Dong and A. Wang, Sci. Rep., 2013, 3, 3532.
23. A. Wang, X. Zhang and M. Zhao, Nanoscale, 2014, 6, 11157–11162.
24. A. Du, S. Sanvito and S. C. Smith, Phys. Rev. Lett., 2012, 108, 197207.
25. X. Zhang, M. Zhao, A. Wang, X. Wang and A. Du, J. Mater. Chem. C, 2013, 1, 6265.
26. X. Li, J. Zhou, Q. Wang, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2013, 4, 259–263.
27. M. W. Zhao, F. C. Pan and L. M. Mei, Appl. Phys. Lett., 2010, 96, 012508.
28. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
31. K. Parlinski, Software PHONON, Cracow.
32. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
33. H. Liu, Y. Liu and D. Zhu, J. Mater. Chem., 2011, 21, 3335.
34. Y. Li, Z. Zhou, P. Shen and Z. Chen, ACS Nano, 2009, 3, 1952–1958.
35. G. Ning, Z. Fan, G. Wang, J. Gao, W. Qian and F. Wei, Chem. Commun., 2011, 47, 5976–5978.
36. Z. Fan, Q. Zhao, T. Li, J. Yan, Y. Ren, J. Feng and T. Wei, Carbon, 2012, 50, 1699–1703.
37. Y. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537–1541.
38. J. Bai, X. Zhong, S. Jiang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 190–194.
39. X. Wang, X. Li, L. Zhang, Y. Yoon, P. K. Weber, H. Wang, J. Guo and H. Dai, Science, 2009, 324, 768–771.
40. X. Li, H. Wang, J. T. Robinson, H. Sanchez, G. Diankov and H. Dai, J. Am. Chem. Soc., 2009, 131, 15939–15944.
41. L. Qu, Y. Liu, J.-B. Baek and L. Dai, ACS Nano, 2010, 4, 1321–1326.
42. Y. Wang, Y. Shao, D. W. Matson, J. Li and Y. Lin, ACS Nano, 2010, 4, 1790–1798.
43. Z.-H. Sheng, L. Shao, J.-J. Chen, W.-J. Bao, F.-B. Wang and X.-H. Xia, ACS Nano, 2011, 5, 4350–4358.
44. W. Zhao, O. Höfert, K. Gotterbarm, J. F. Zhu, C. Papp and H. P. Steinrück, J. Phys. Chem. C, 2012, 116, 5062–5066.
45. Q. Min, X. Zhang, X. Chen, S. Li and J. J. Zhu, Anal. Chem., 2014, 86, 9122–9130.
46. P. Kuhn, A. Forget, D. Su, A. Thomas and M. Antonietti, J. Am. Chem. Soc., 2008, 130, 13333–13337.
47. T. V. Tam, N. B. Trung, H. R. Kim, J. S. Chung and W. M. Choi, Sens. Actuators, B, 2014, 202, 568–573.
48. Y. Wang, X. Wang and M. Antonietti, Angew. Chem., Int. Ed., 2012, 51, 68–89.
49. T. Mu, J. Huang, Z. Liu, B. Han, Z. Li, Y. Wang, T. Jiang and H. Gao, J. Mater. Res., 2011, 19, 1736–1741.
50. G. Dong, K. Zhao and L. Zhang, Chem. Commun., 2012, 48, 6178–6180.
51. C. Wu and S. Das Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235107.
52. E. Kan, W. Hu, C. Xiao, R. Lu, K. Deng, J. Yang and H. Su, J. Am. Chem. Soc., 2012, 134, 5718–5721.
53. Z. F. Wang, N. Su and F. Liu, Nano Lett., 2013, 13, 2842–2845.

---