Light trapping in hematite-coated transparent particles for solar fuel generation

Abstract

Hematite (α-Fe₂O₃), due to its abundance and low-cost, is an attractive compound for photoelectrochemical splitting of water to produce hydrogen. However, one major obstacle preventing hematite from achieving the target efficiencies comprises its significantly smaller minority carrier transport distance relative to its optical absorption depth in the visible part of the optical spectrum. Here, we combine host–guest and Mie resonance concepts to achieve significant optical absorption in extremely thin layers of hematite. We propose and theoretically evaluate transparent particles coated with an extremely thin hematite shell as building blocks for hematite photoanodes. By full-field optical simulations we found out that maximal optical absorption is achieved when the particle supports two to three Mie resonance modes above the hematite optical absorption edge. Optical absorption efficiencies integrated over the air mass 1.5 global (AM1.5G) irradiance spectrum, 〈η_abs〉_AM1.5, reach more than 2 mA cm⁻² within a 10 nm thick hematite shell of a particle with optimal dimensions and 〈η_abs〉_AM1.5 comes close to 5 mA cm⁻² in a 25 nm thick hematite shell. Furthermore, we evaluate the performance when the particles are part of an array or stacked atop each other. The concept introduced here could be useful for improving optical absorption in semiconductors with extremely short carrier transport distances.

---

1 Introduction

Achievement of more than 5% solar to hydrogen efficiency in a solar hydrogen production device comprising a bismuth vanadate (BiVO₄) photoelectrochemical (PEC) device biased with a double junction thin film silicon solar cell^1,2 has illustrated the bright future for PEC cells in hydrogen production. Despite such progress with BiVO₄ (ref. 1–5) and also with compounds such as Ta₃N₅ (ref. 6–8) and oxynitrides,^9–11 α-Fe₂O₃, or hematite, is still the most attractive water oxidation semiconductor due to its earth-abundance and optical absorption edge of about 620 nm.^12,13

To achieve highly efficient hematite photoanodes a number of approaches have been pursued so far to bypass the short minority carrier transport distance of 10 nm in hematite.¹³ Networks of hematite nanowires,^14–16 host–guest approaches,^17–19 mesoporous hematite layers,^20,21 plasmonic nanostructures,^22,23 and using a reflective back-contact²⁴ are among the different approaches that have been pursued. In addition, several sophisticated light trapping approaches have been recently proposed for hematite in which Mie resonance and/or host–guest approach(es) are used.^17,25–29

Here, we propose a photoanode design in which we combine the host–guest approach with Mie resonance optical absorption. The host–guest approach is a method in which a thin layer of hematite is conformally coated onto a nanostructured conductive framework or onto an appropriate semiconductor with a large surface area. Mie resonances provide strong light trapping due to the optical resonance effect and they are identified by having a large portion of their energy density close to the particle center; something that is not ideal for hematite because only optical absorption for a hematite distance of 10 nm away from the hematite/electrolyte (EL) interface contributes to the water splitting process. For this reason, the Mie resonators we propose here comprise a transparent (for instance anatase TiO₂) core with a thin Fe₂O₃ shell. Transparency of the core is essential in building stacks of these spherical particles because the energy of light will not be dissipated within the core and therefore it can reach the layers underneath. On resonance the incident light is trapped inside the particle, the photon circulates within the particle, and hence light interaction with the hematite shell is enhanced. We optimize the dimensions of TiO₂ particles coated with extremely thin layers of hematite (TiO₂@hematite) to maximize the optical absorption within hematite. Furthermore, we evaluate the absorption efficiency of TiO₂@hematite particles integrated over the air mass 1.5 global (AM1.5G) irradiance spectrum. We explore and identify the parameter space giving maximal sunlight absorption within the carrier collection volume of hematite, described by a shell of 10 nm distance from the Fe₂O₃/EL interface. In addition, we evaluate optical absorption in stacks or in an array of these particles to take into account the effect of multilayer formation and particle packing.

2 Results and discussion

Fig. 1(a) shows a schematic of TiO₂@hematite particles studied in this work in which the carrier collection volume is distinguished from the rest of the hematite by a dashed line. The entire volume, illustrated by light-red color and defined by a shell of 10 nm distance from the hematite/EL interface, designates the volume from which the photogenerated electron–hole pairs can be extracted with nearly 100% efficiency. The optical absorption edge of anatase TiO₂ is about 3.2 eV (ref. 30), therefore it does not absorb visible light and as for ultraviolet light, it is absorbed in the hematite shell before reaching TiO₂. Therefore, we design the particle dimensions such that they support weakly localized or low quality factor (low-Q) Mie resonance modes in the visible part of optical spectrum so that their electric field profile has a large overlap with the hematite shell.

Fig. 1 (a) Schematic of the cross-section of a TiO₂@hematite particle in which the 10 nm carrier collection volume of hematite is illustrated. (b) Configuration of the hematite photoanode proposed in this work comprising a multilayer of resonant-size transparent (here TiO₂) particles coated with a thin shell of hematite. Such a configuration is proposed based on a successful, extremely thin hematite device presented in the past.³¹

The basic schematic of a photoanode that can be built from these core–shell TiO₂@hematite particles is depicted in Fig. 1b. It comprises a standard transparent conductive oxide (TCO) layer; i.e. F:SnO₂, also called fluorinated tin oxide (FTO), coated on glass. Directly on top of FTO there is an ultrathin (about 2 to 3 nm-thick) layer of Nb₂O₅ (ref. 31) that can be deposited by atomic layer deposition (ALD)^31,32 or chemical vapour deposition (CVD).^33,34 A 10 nm-thick hematite layer deposited by ALD on the Nb₂O₅ layer has been reported to result in about 0.5 mA cm⁻² photocurrent density at 1.23V_RHE under 1 sun illumination.³¹ V_RHE defines the reversible hydrogen electrode potential. Such a photoanode can be coated by a monolayer or several layers of the TiO₂@hematite particles studied in this work, as shown in Fig. 1, to boost the optical absorption while keeping the distance that minority carriers need to travel short.

From a practical point of view, there are well-established processes to produce TiO₂ spherical particles of controlled diameter³⁵ that are useful for the concept introduced here. Then, hematite can be coated onto these particles by, for instance, fluidized-bed ALD processes.^36,37 The particles can be fixed onto the substrate by sintering processes that are common in the synthesis of hematite photoanodes.²¹

We begin by modeling the interaction of light with isolated TiO₂@hematite particles. From the electromagnetic theory of spheres,³⁸ also known as Mie theory, we expect these spheres to support resonance modes at sub-wavelength and wavelength scale dimensions. These resonance modes lead to resonant optical antenna effects that significantly enhance the optical absorption.^39–42 These optical antenna effects also occur in non-spherical dielectric and semiconductor structures in which the modal properties are described in the framework of the recently established leaky mode resonance theory.^39,40,43

In spherical geometry the electromagnetic fields are expanded as the sum of spherical eigenmodes generally described as

ψ_nml = b_l(kr)p^m_lcos(θ)exp(±imϕ) (1)

where b_l(kr) is the spherical Bessel function and p^m_l(cos θ) is the associated Legendre function. Every spherical eigenmode is described by a set of (n, l, m) numbers where n is the number of field maxima inside the sphere in the radial direction, l is the polar, and m is the azimuthal mode numbers. The number of anti-nodes in the radial direction is described as the n quantum number and it is obtained from the zeros of b_l(kr). In the polar direction, along the θ-axis, the number of anti-nodes is obtained by (m − l + 1).^38,44

In our calculations we model sunlight as a plane wave described by E⃑_inc = E⃑₀ exp(−ik⃑·r⃑), where k⃑ is the wave-vector of the plane wave related to its frequency by and k⃑·r⃑ = kx given the configuration shown in Fig. 2a. The optical constants; i.e. refractive index and permittivity data, of Fe₂O₃ are acquired from the literature.⁴⁵ Complex refractive index data of TiO₂ and Fe₂O₃ are reported in the ESI.†

Fig. 2 (a) Schematic of a TiO₂@hematite spherical particle under plane wave excitation in which the coordinate is defined. (b) Absorption efficiency spectra for TiO₂@hematite particles with hematite shells of 10 nm and TiO₂ particle sizes of 200 nm, 300 nm, and 400 nm. Profile of (c) electric field amplitude and (d) dissipated power density in 200 nm TiO₂ particles with 10 nm hematite shells at four different wavelengths corresponding to the peaks and valleys of the absorption efficiency spectrum shown in part (b). (e) Profile of dissipated power density (P_d = E⃑·J⃑) in 300 nm TiO₂ particles with 10 nm hematite shells at four different wavelengths corresponding to the peaks in the absorption efficiency spectrum shown in part (b).

Interaction of this plane wave with isolated TiO₂@hematite particles in water is modeled at each wavelength in the 300–620 nm range by numerically solving full-field Maxwell equations using the finite element method (FEM). We solve the equations for scattered fields using a tetrahedral mesh and a perfectly matched layer (PML) boundary condition. The direct band gap of hematite is often reported between 1.9 and 2.2 eV (ref. 12) and here we consider a 2 eV direct bandgap for hematite in our calculations. Electromagnetic fields calculated by FEM simulations are then used for calculating the absorption efficiency η = C_abs/C_geom where C_abs is absorption cross-section and C_geom is geometrical cross-section of the TiO₂@hematite particles.⁴⁶ C_abs is described by the ratio of absorbed power P_abs in the particle, P_abs = ∫J⃑(r⃑, λ)·E⃑(r⃑, λ)d³r to the intensity of the incident light . J⃑(r⃑, λ) describes the Ohmic electric current induced by electromagnetic waves in the hematite shell and P_d = J⃑(r⃑, λ)·E⃑(r⃑, λ) describes the dissipated power density in (W m⁻³).

Fig. 2b shows the absorption efficiency spectra for TiO₂ particles of 200 nm, 300 nm, and 400 nm diameter coated with 10 nm thick hematite shells. In the optical absorption efficiency spectrum of the 200 nm TiO₂ particle, two peaks appear that are labeled as zeroth (m = 0) and first (m = 1) order Mie resonance modes. At wavelengths shorter than 620 nm, i.e. the direct absorption edge of hematite, three and four peaks are observed in the absorption spectra of 300 nm and 400 nm TiO₂ particles, respectively. Comparison of these three spectra shows that (i) the number of resonance peaks increases as the particle size becomes larger and (ii) coupling of the incident light to the hematite shell is largest for the 300 nm TiO₂ particles. The coupling extent is quantified by the amplitude of the absorption efficiency.

Profiles of the electric field amplitude at peaks and valleys of the absorption efficiency spectrum of the 200 nm TiO₂ particles are depicted in Fig. 2c. At peak wavelengths, the overlap of electric field with the hematite shell is strong whereas at the valleys this overlap is weak. This reconfirms the weak absorption in the valley positions because optical absorption is proportional to the intensity of the electric field, i.e. electric field amplitude squared. This is more clearly illustrated in Fig. 2d in which dissipated power densities (P_d = E⃑·J⃑) over the entire particle cross section are depicted.

We label the resonance modes based on the number of nodes in the profile of dissipated power density in hematite along the azimuthal direction. For instance, the zeroth Mie mode has no node within the hematite shell whereas the first Mie mode has two nodes. Higher order Mie modes, i.e. second and third order modes, are excited in 300 nm TiO₂ particles with 10 nm hematite shells. Fig. 2e shows P_d profile in which the second (m = 2) order mode is identified by four nodes and the third order (m = 3) resonance modes by six nodes.

To evaluate the broadband optical absorption in TiO₂@hematite particles over the entire absorption band of hematite (λ < 620 nm) we calculate the integrated weighted absorption efficiency described by^42,47–49

where ϕ_AM1.5 describes the irradiance spectrum of standard air mass AM1.5G illumination. 〈η_abs〉_AM1.5 basically describes the ratio of the number of photons absorbed in hematite to the total amount of the above band gap photon flux passing through the geometrical cross-section of the particle.

Fig. 3a–c show the calculated 〈η_abs〉_AM1.5 in the 10 nm outer hematite shell, in the entire hematite shell, and the difference between these two. Three peaks appear in the 〈η_abs〉_AM1.5 profile as TiO₂ particle size and hematite shell thickness vary from 100–500 nm and from 10–25 nm, respectively. The first peak corresponds to the case in which two Mie resonances exist in the 300–620 nm wavelength range. The second and the third peaks correspond to the cases in which three and four Mie resonance peaks exist in the wavelength range of interest for hematite.

Fig. 3 Integrated AM1.5G weighted absorption efficiency (a) in the outer 10 nm hematite shell, (b) in the entire hematite, and (c) the difference of the two as the size of the TiO₂ particles varies from 100 nm to 500 nm at shell thicknesses of 10 nm, 15 nm, 20 nm, and 25 nm.

〈η_abs〉_AM1.5 values in the 10 nm outer hematite shell show maxima slightly larger than 2 mA cm⁻² for all hematite shell thicknesses as the TiO₂ particle size varies (Fig. 3a). To determine the optimal thickness of the hematite shell we need to minimize the portion of optical energy that is absorbed in part of hematite that is not within the current collection volume because this energy is dissipated and it does not contribute to the water splitting process. Therefore, we can conclude that given the 10 nm minority carrier transport distance in hematite, the 10 nm hematite shell is ideal. The energy loss becomes important when we make a multilayer of these TiO₂@hematite particles because in thicker hematite shells a large portion of optical energy is dissipated within the first few layers of these particles (Fig. 3c).

Fig. 3b shows 〈η_abs〉_AM1.5 in the entire hematite shell, revealing that the particles delivering maximal optical absorption have overall dimensions of 200 nm to 320 nm. In these dimensions two or three Mie resonance modes are excited in the particles in the 300–620 nm wavelength range. The total 〈η_abs〉_AM1.5 reaches nearly 5 mA cm⁻² under these conditions highlighting the efficient optical absorption in properly designed TiO₂@hematite particles. We should mention that such a high optical absorption becomes interesting if the hole diffusion length of hematite could be extended to 25 nm, for instance by using impurity doping.⁵⁰

Stacks of several of these particles need to be used to achieve larger photocurrent densities, therefore, to obtain an estimate of how stacking influences the 〈η_abs〉_AM1.5 values we study a stack of two TiO₂@hematite particles. We consider two optimal 220 nm TiO₂@hematite particles with either 10 nm or 20 nm hematite shell thicknesses. Fig. 4b shows the absorption efficiency of a stack of two 200 nm TiO₂ particles with 10 nm hematite shells along with the absorption efficiencies of each sphere. The profiles of absorption efficiencies for individual particles and also for the stack of two particles are somewhat different from the absorption efficiency profile of a single particle shown in Fig. 2b. This indicates that in the two particles the scattered light from each particle interacts with the other particle and therefore Mie resonance is not the only mechanism involved. The absorption efficiency of the first particle (P1) is significantly larger than the absorption efficiency of a single particle (Fig. 2b) whereas in the second one (P2) the absorption efficiency is smaller.

Fig. 4 (a) Schematic illustrating two stacked TiO₂@hematite particles illuminated by a plane-wave in which the particles exposed to the light first and second are designated as P1 and P2. (b) Absorption efficiency spectra of a stack of two 200 nm TiO₂ particles with 10 nm hematite shells. In the graph, the contribution of optical absorption in each particle is specified. The bar in the inset shows 〈η_abs〉_AM1.5 of the stack and also the contribution of each particle. (c) Absorption efficiency spectra of a stack of two 180 nm TiO₂ particles with 20 nm hematite shells. In the graph, the contribution of optical absorption in each particle is specified; the solid line designates the optical absorption in the 10 nm outer shell whereas the dashed line designates the optical absorption within the 10 nm inner shell. (d) The bar on the left (right) shows 〈η_abs〉_AM1.5 within the 10 nm outer (inner) hematite shells.

The 〈η_abs〉_AM1.5 data were calculated for each particle and also for the stack of two particles and they are depicted as the bar chart shown in the inset of Fig. 4b. 〈η_abs〉_AM1.5 in P1, P2, and the stack of two particles are 3.6, 0.98, and 4.6 mA cm⁻² as shown in the inset of Fig. 4b. We should note that 4.6 mA cm⁻² is produced in a hematite volume with nearly 100% carrier collection efficiency. Fig. 4c shows the absorption efficiencies of the 10 nm inner/outer hematite shells for the stack of two 180 nm TiO₂ particles with 20 nm hematite shells along with the same data for each particle. This shows that a total of 7 mA cm⁻² of AM1.5G light is absorbed in hematite out of which only 3.6 mA cm⁻² is generated within 10 nm from the hematite/EL interface. This is clearly smaller than the 4.6 mA cm⁻² that is generated in the stack of two 200 nm TiO₂ particles with 10 nm hematite shells. In addition, an equivalent of 3.4 mA cm⁻² is dissipated in hematite, which cannot be recovered even if we use extra layers of the particles.

In an actual PEC device, an array or a stack of arrays of a large number of TiO₂@hematite particles is used (Fig. 1). Therefore, we need to evaluate how the presence of adjacent particles influences the optical absorption mechanism. Previous studies,^45,47 both theoretical and experimental, have shown that the results of isolated particles cannot be directly translated to large area devices composed of a large number of particles. This is due to two reasons: (i) coupling among adjacent particles^47–49 and (ii) the presence of Fabry–Perot resonance modes in an ordered array of dielectric particles.^41,47,51

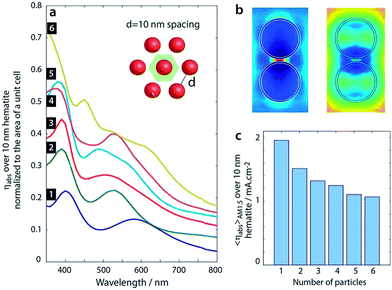
To take the effect of adjacent particles into account we model the interaction of a plane wave with 2 to 6 TiO₂ (200 nm)@hematite (10 nm) particles packed in a hexagonal configuration with 10 nm spacing among the two particles, as shown in the inset of Fig. 5a. The absorption efficiency was calculated by normalizing the absorption cross-section to the area of a unit cell and is depicted in Fig. 5a. The unit cell is designated with a green hexagon in the inset of Fig. 5a. The profile of absorption efficiency of these clusters of particles is no longer the same as the one of a single particle. Several extra peaks appear in the absorption efficiency spectrum, arising from coupling among adjacent particles. The electric field amplitude profile at the peaks of absorption efficiency for the case of the 2-particle cluster does not show a Mie resonance profile but it arises from the even and odd coupled modes of the particles. The profile in which the electric field is maximal between the two particles is similar to the even (symmetric) mode and the other in which the electric field is rather stronger inside the particles comprises the odd (asymmetric) modal characteristics.

Fig. 5 (a) Optical absorption efficiency spectra of an array of one to six TiO₂ (200 nm)@hematite (10 nm) particles with 10 nm separation. Incident light impinges on the array from out of the plane. (b) The electric field profile at the position of the peaks of absorption efficiency spectra of two particles. (c) Integrated optical absorption efficiency normalized to the unit cell area for a hexagonal array of up to six of these TiO₂@hematite particles with 10 nm spacing.

We further evaluate the influence of these adjacent particles on the overall AM1.5G integrated optical absorption by calculating 〈η_abs〉_AM1.5 for the clusters of 2 to 6 particles with 10 nm interspacing between the particles. Fig. 5c shows 〈η_abs〉_AM1.5 and illustrates that due to the presence of adjacent particles the overall absorption decays from about 2 mA cm⁻² for a single particle to 1.15 mA cm⁻² for a cluster of 6 particles. Extrapolating the data results in slightly more than 1 mA cm⁻² for an infinite array of these particles. Therefore, we expect a minimum of 1 mA cm⁻² photocurrent for a monolayer of optimized 200 nm TiO₂ particles with 10 nm hematite shells.

3 Conclusion

Through full-field optical calculations, we have shown that transparent particles coated with an extremely thin layer of hematite, if designed properly, efficiently absorb light within the 10 nm carrier transport distance of hematite. We found that the main critical design parameter is the overall size of the particle, which should be large enough so that the particle supports two to three Mie resonance modes above the bandgap of hematite; i.e. the 300–620 nm wavelength range. In the stack of two particles, the performance scales linearly with the number of particles implying that a multilayer of these particles can be used for achieving maximal optimal absorption while keeping the distance that the minority carriers need to travel fixed. The presence of other particles in the vicinity of the particle deteriorates the optical absorption by nearly a half. This is the situation that takes place when we build an actual PEC electrode from a large number of these particles. These particles can be synthesized using a combination of polyol and liquid-/gas-phase deposition methods and once synthesized, they can be applied to the fabrication of large area devices using low-cost printing processes. Therefore, the concept of transparent particles with a light-absorbing semiconductor shell can be applied for enhancing optical absorption in solar energy materials with short carrier transport distances.

Acknowledgements

The authors thank Prof. A. Moshaii in the Department of Physics, Tarbiat Modarres University for providing computational facilities.

References

1. F. F. Abdi, L. Han, A. H. M. Smets, M. Zeman, B. Dam and R. van de Krol, Nat. Commun., 2013, 4, 2195.
2. L. Han, F. F. Abdi, R. van de Krol, R. Liu, Z. Huang, H. Lewerenz, B. Dam, M. Zeman and A. Smets, ChemSusChem., 2014, 7, 2832–2838.
3. F. F. Abdi and R. van de Krol, J. Phys. Chem. C, 2012, 116, 9398.
4. F. F. Abdi, N. Firet, A. Dabirian and R. van de Krol, MRS Proc., 2012, 1446,  DOI:10.1557/opl.2012.811.
5. F. F. Abdi, A. Dabirian, B. Dam and R. van de Krol, Phys. Chem. Chem. Phys., 2014, 16, 15272.
6. A. Dabirian and R. van de Krol, Appl. Phys. Lett., 2013, 102, 033905.
7. M. Higashi, K. Domen and R. Abe, Energy Environ. Sci., 2011, 4, 4138.
8. Y. Li, T. Takata, D. Cha, T. Minegishi, J. Kubota and K. Domen, Adv. Mater., 2013, 25, 125.
9. M. Higashi, K. Domen and R. Abe, J. Am. Chem. Soc., 2012, 134, 6968.
10. K. Maeda, M. Higashi, B. Siritanaratkul, R. Abe and K. Dome, J. Am. Chem. Soc., 2011, 133, 12334.
11. A. Dabirian, H. van’t Spijker and R. van de Krol, Energy Procedia, 2012, 22, 15.
12. J. H. Kennedy and K. W. Frese, J. Chem. Sci., 1978, 125, 709–714.
13. K. Sivula, F. Le Formal and M. Grätzel, ChemSusChem., 2011, 4, 432.
14. J. Y. Kim, G. Magesh, D. H. Youn, J. Jang, J. Kubota, K. Domen and J. S. Lee, Sci. Rep., 2013, 3, 2684.
15. D. A. Wheeler, G. Wang, Y. Ling, Y. Li and J. Z. Zhang, Energy Environ. Sci., 2012, 5, 6682.
16. Y. Ling, G. Wang, D. A. Wheeler, J. Z. Zhang and Y. Li, Nano Lett., 2011, 11, 2119.
17. Y. Qiu, S. Leung, Q. Zhang, B. Hua, Q. Lin, Z. Wei, K. Tsui, Y. Zhang, S. Yang and Z. Fan, Nano Lett., 2014, 14, 2123.
18. K. Sivula, F. L. Formal and M. Grätzel, Chem. Mater., 2009, 21, 2862.
19. Y. Lin, S. Zhou, S. W. Sheehan and D. Wang, J. Am. Chem. Soc., 2011, 133, 2398.
20. S. D. Tilley, M. Cornuz, K. Sivula and M. Grätzel, Angew. Chem., Int. Ed., 2010, 122, 6549.
21. K. Sivula, R. Zboril, F. Le Formal, R. Robert, A. Weidenkaff, J. Tucek, J. Frydrych and M. Grätzel, J. Am. Chem. Soc., 2010, 132, 7436.
22. I. Thomann, B. A. Pinaud, Z. Chen, B. M. Clemens, T. F. Jaramillo and M. L. Brongersma, Nano Lett., 2011, 11, 3440.
23. M. Akbari, M.-R. Kikhavani, K. Sheshyekani and A. Dabirian, RSC Adv., 2013, 3, 17837.
24. H. Dotan, O. Kfir, E. Sharlin, O. Blank, M. Gross, I. Dumchin, G. Ankonina and A. Rothschild, Nat. Mater., 2013, 12, 158.
25. K. X. Wang, Z. Yu, V. Liu, M. L. Brongersma, T. F. Jaramillo and S. Fan, ACS Photonics, 2014, 1, 235.
26. M. L. Brongersma, Y. Cui and S. Fan, Nat. Mater., 2014, 13, 451.
27. S. J. Kim, I. Thomann, J. Park, J. Kang, A. P. Vasudev and M. L. Brongersma, Nano Lett., 2014, 14, 1446.
28. F. Boudoire, R. Toth, J. Heier, A. Braun and E. C. Constable, Energy Environ. Sci., 2014, 7, 2680.
29. S. Ramadurgam, T. Lin and C. Yang, Nano Lett., 2014, 14, 4517.
30. T. Tang, K. Prasad, R. Sanjines, P. E. Schmid and F. Levy, J. Appl. Phys., 1994, 75, 2042.
31. T. Hisatomi, H. Dotan, M. Stefik, K. Sivula, A. Rothschild, M. Grätzel and N. Mathews, Adv. Mater., 2012, 24, 2699.
32. S. M. George, Chem. Rev., 2010, 110, 111.
33. A. Dabirian, Y. Kuzminykh, E. Wagner, G. Benvenuti, S. A. Rushworth and P. Hoffmann, ChemPhysChem, 2011, 12, 3524.
34. A. Dabirian, Y. Kuzminykh, E. Wagner, G. Benvenuti, S. A. Rushworth and P. Hoffmann, Thin Solid Films, 2014, 571, 94.
35. X. Jiang, T. Herricks and Y. Xia, Adv. Mater., 2003, 15, 1205.
36. J. R. Scheffe, A. Francés, D. M. King, X. Liang, B. A. Branch, A. S. Cavanagh, S. M. George and A. M. Weimer, Thin Solid Films, 2009, 517, 1874.
37. A. B. F. Martinson, M. J. DeVries, J. A. Libera, S. T. Christensen, J. T. Hupp, M. J. Pellin and J. W. Elam, J. Phys. Chem. C, 2011, 115, 4333.
38. L. Tsang, J. A. Kong and K. Ding, Scattering of Electromagnetic Waves, Theories and Applications, Wiley Interscience, 2000.
39. L. Cao, J. S. White, J. Park, J. A. Schuller, B. M. Clemens and M. L. Brongersma, Nat. Mater., 2009, 8, 643.
40. L. Cao, P. Fan, A. P. Vasudev, J. S. White, Z. Yu, W. Cai, J. A. Schuller, S. Fan and M. L. Brongersma, Nano Lett., 2010, 10, 439.
41. S. Kim, R. W. Day, J. F. Cahoon, T. J. Kempa, K. Song, H. Park and C. M. Lieber, Nano Lett., 2012, 12, 4971.
42. S. A. Mann and E. C. Garnett, Nano Lett., 2013, 13, 3173.
43. Y. Yu and L. Cao, Opt. Express, 2012, 20, 13847.
44. A. Dabirian and N. Taghavinia, RSC Adv., 2013, 3, 25417.
45. J. A. Glasscock, P. R. F. Barnes, I. C. Plumb, A. Bendavid and P. J. Martin, Thin Solid Films, 2008, 516, 1716.
46. C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, 1983.
47. T. J. Kempa, R. W. Day, S. Kim, H. Park and C. M. Lieber, Energy Environ. Sci., 2013, 6, 719.
48. Y. Yu, V. E. Ferry, A. P. Alivisatos and L. Cao, Nano Lett., 2012, 12, 3674.
49. X. Zhang, C. W. Pinion, J. D. Christesen, C. J. Flynn, T. A. Celano and J. F. Cahoon, J. Phys. Chem. Lett., 2013, 4, 2002.
50. J. A. Glasscock, P. R. F. Barnes, I. C. Plumb and N. Savvides, J. Phys. Chem. C, 2007, 11, 16477.
51. A. Dabirian, J. Opt., 2014, 16, 075001.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra15848b

‡ These authors contributed equally to this work.

---