An experimental and theoretical study of the kinetics of the reaction between 3-hydroxy-3-methyl-2-butanone and OH radicals

Abstract

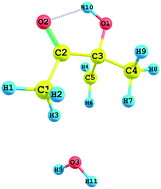
Absolute experimental and theoretical rate constants are determined for the first time for the reaction of 3-hydroxy-3-methyl-2-butanone (3H3M2B) with OH radicals as a function of temperature. Experimental studies were carried out over the temperature range of 277 to 353 K and the pressure range of 5 to 80 Torr, by using a cryogenically cooled cell coupled to the PLP-LIF technique. OH radicals were generated for the first time from the photodissociation of the reactant 3H3M2B at 266 nm and the OH formation yield in 3H3M2B photolysis at 266 nm was measured under our experimental conditions. In addition, the reaction of 3H3M2B with OH radicals was studied theoretically by using the Density Functional Theory (DFT) method under three hydrogen abstraction pathways. According to these calculations, H-atom abstraction occurs more favourably from the methyl group adjacent to the hydroxyl group with a small barrier height. The calculated theoretical rate constants are in good agreement with the experimental data over the temperature range of 278 to 1000 K. No significant temperature dependence can be observed although a very slight effect was observed within the error bars.