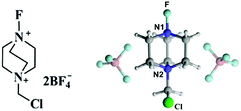
Theoretical study on the mechanism of selective fluorination of aromatic compounds with Selectfluor

Abstract

The selective fluorination of aromatic compounds with Selectfluor has been studied theoretically. The structural and energetic features of π complexes of substituted benzenes with Selectfluor are investigated, and the fluorine bond (F⋯π) has been found to make an important contribution to the stabilization of the π complexes. Our calculations indicate that the SET mechanism, which involves one electron transfer from the aromatic substrate (D) to Selectfluor (A), is preferred over the S_N2 mechanism. The analysis of the minimum energy path (MEP) suggests that the DABCO moiety of Selectfluor seems to take an active role in the fluorination of aromatic compounds with Selectfluor. In addition, a two-state model analysis, as well as the characteristics of avoiding crossing between the DA and D⁺A⁻ states of benzene/Selectfluor are addressed to obtain deep insight into the features of the SET mechanism.

---

1. Introduction

Fluorinated aromatic compounds have attracted growing interest due to their extensive application as pesticides, medicinal agents, and various functional materials.^1–3 Thus, the development of mild and selective synthetic methods for incorporating fluorine into organic aromatic compounds is of great importance. Recently, the N–F reagents with common structures of R₂N–F or R₃N–F are increasingly applied to selective fluorination of aromatic compounds,^4–10 since they are stable and easy to handle. Among many electrophilic N–F reagents, the commercially available 1-chloromethyl-4-fluoro-1,4-iazoniabicyclo[2.2.2]octanebis-tetra-fluoroborate (F-TEDA-BF₄, Selectfluor) is the most popular one (Scheme 1).^11,12

Scheme 1 The typical skeleton structure and related optimized geometry of Selectfluor.

Selectfluor is usually considered as sources of ‘pseudopositive’ or ‘electrophilic’ fluorine involved in the fluorination process of aromatic compounds (Scheme 2).¹³ Two mechanisms, the nucleophilic substitution (polar mechanism, S_N2) and single-electron transfer (SET) mechanism, have been proposed to interpret this electrophilic fluorination reaction.^12,14 Differding and coworkers^15,16 have reported several studies concerning the mechanism of fluorination using N–F reagents to support the S_N2 mechanism. Later, based on the observed ESI-MS and ESI-MS/MS spectra data, Zhang¹⁷ suggested that the fluorination reactions of triphenylethylene and tetraphenylethylene with Selectfluor proceed via the SET mechanism. Stavber and coworkers⁶ also proposed that single electron transfer (SET) is the dominant process in the functionalization of methyl-substituted benzene derivatives with Selectfluor. Complementally, the possibility of SET mechanism for some electrophilic aromatic substitutions has also been discussed previously.^18–20 Recently, more clear evidences for SET mechanism between Selectfluor and chloride were reported.²¹ However, no definitive mechanism of electrophilic aromatic fluorination reaction with Selectfluor has been identified at present.

Scheme 2 Fluorination of aromatic compounds with Selecfluor, where X = F, H, CH₃, NH₂ etc.

In this work, a systematic theoretical investigation of the fluorination reaction for a few aromatic compounds with Selectfluor was performed by computational analysis. The spin density maps (SDM) was used to predict sites of higher reactivity and interpret the observed regiochemistry for the fluorination reactions. The molecular electrostatic potential (ESP) of Selectfluor was displayed to characterize the nature of non-covalent interactions between Selectfluor and the aromatic compounds. The Bader's atoms in molecules (AIM) approach, as well as natural bond orbital (NBO) analysis were also applied to understand the non-covalent interactions of the π complexes. Moreover, the exploration of the minimum energy path (MEP) provides more details about the fluorination of aromatic compounds with Selectfluor. In order to get a direct view of the inner-sphere SET process, the characters of the charge localized diabatic states along the fluorine transfer pathway are also discussed.

2. Theoretical methods

Considering M06-2X provides reasonable energetics of non-bonded interactions,^22,23 the geometries of all minima and transition states for the fluorination of aromatic compounds with Selectfluor were computed at the M06-2X/6-311++G** level. The frequency calculations were carried out at the same level to identify all of the stationary points as minima (zero imaginary frequencies) or first-order saddle points (one imaginary frequency). The intrinsic reaction coordinate (IRC)²⁴ calculations were performed to confirm that the optimized transition states correctly connect the relevant reactants and products. All the variances of the geometrical parameters, Mulliken charge and vibrational frequencies along the IRC for the aromatic fluorination were analysed. Natural bond orbital (NBO) analysis²⁵ was carried out to study the nature of bonding in the π complexes. And binding energies of π complexes were calculated by taking into account of the basis set superposition error (BSSE)²⁶ and thermal corrections. The spin density maps (SDM) of the aromatic ring radical cations were used to interpret the observed regioselectivity in the fluorination reactions. Solvent effects (acetonitrile) have been considered at the M06-2X/6-311++G** level using the polarizable continuum model (PCM),²⁷ and single-point energies in acetonitrile were combined with gas phase thermal correction computed at the same level of theory. Unless specifically mentioned, the reported energies are Gibbs free energies with thermal corrections. Free energies were evaluated based on the molecular partition functions derived from the rigid-rotor and harmonic oscillator approximations. Then, the relative free energy is given by the following equation:

ΔG = ΔU + ΔH_tr + ΔH_rot + ΔH_vib − TΔS

ΔS = ΔS_tr + ΔS_rot + ΔS_vib

All calculations were carried out using the GAUSSIAN 09 program.²⁸

The atoms in molecules (QTAIM) analysis²⁹ was performed at M06-2X/6-311++G** level, using AIMALL program.³⁰ The energy decomposition analysis (EDA) is a powerful method for quantitative interpretation of the interaction energy. Here, the localized molecular orbital energy decomposition (LMO-EDA) analysis³¹ implemented in GAMESS (US)³² was used to study non-covalent interactions. In addition, a two-states model analysis is performed for the SET mechanism, and the constrained DFT calculations were adopted to map out the potential energy curves along the fluorine transfer process for the charge localized diabatic states.^33,34 Furthermore, the Löwdin population was used to constrain the charge as implemented in NWCHEM package³⁵ at M06-2X/6-31G* level.

3. Results and discussions

3.1 Evaluation of density functionals

It was reported that M06-2X performs well for main-group thermochemistry, barrier heights, and noncovalent interactions.^22,23 In order to examine the effects of different density functionals on the fluorination reaction, we select M06-2X and other seven well-known and/or recently developed density functionals including B3LYP,³⁶ B3PW91,³⁷ B97D,³⁸ X3LYP,³⁹ M05-2X,²³ B2PLYP,⁴⁰, and LC-ωPBE,⁴¹ to calculate the energy barriers of the fluorination of aniline starting with the structures optimized at the M06-2X/6-311++G(d,p) level of theory in gas phase. The results are shown in Table 1. Clearly, M06-2X is satisfactory in predicting the electronic energy barriers of the fluorination because its deviation of activation energy from the average value is very small. It can also be seen that in each case, TS1^SET is more stable than TS1^S_N2 by over 3 kcal mol⁻¹, suggesting that the SET mechanism is more favorable than the S_N2 mechanism. In addition, the optimized structure of Selectfluor using the M06-2X/6-311++G** method is very close to the MP2/cc-pVTZ geometry as well as its X-ray crystallographic structure (See Table S1†),⁴² which indicates that the M06-2X with the 6-311++G** basis set was a suitable method for the following investigation on the mechanism of the fluorination with Selectfluor.

Table 1 The absolute electronic energy (E, a.u.) for the transition state structure of the rate-determining step (σ-complex formation) in S_N2 and SET mechanism, and the electronic energy difference (ΔE = E(SET) − E(S_N2), kcal mol⁻¹). The SET mechanism is preferred at different theoretical level

	E(SN2)	E(SET)	ΔE
M06-2X	−2080.9851	−2080.9982	−8.2
B3lyp	−2081.6088	−2091.6136	−3.0
B3pw91	−2080.9122	−2081.9171	−3.1
Lc-wpbe	−2080.4592	−2080.4843	−15.8
B97D	−2080.6832	−2080.6933	−6.3
X3LYP	−2080.9602	−2080.9659	−3.6
M05-2X	−2080.4419	−2080.4594	−11.0
B2plyp	−2078.5547	−2080.5818	−17.0

---

3.2 π complexes

The reaction between Selectfluor and aromatic compounds begins with the formation of π complexes.⁴³ In this section, several aromatic compounds (including fluorobenzene, benzene, toluene, aniline) have been selected to interact with Selectfluor, aiming to characterize the structural, energetic and electron features of π complexes.

3.2.1 The electrostatic potential of Selectfluor. To investigate how Selectfluor interacts with aromatic compounds, the molecular ESP iso-surface of Selectfluor has been extracted (Fig. 1). We focus on the N1–F region of Selectfluor, where the electrostatic potentials around F are all positive with a slightly more positive cap (σ-hole) which is narrowly confined on the elongation of the N1–F covalent bond axis.^44,45 Herein, the ESP value at the positive cap (V_max) is calculated to be 22.03 kcal mol⁻¹.^46,47 Evidently, although the degree of polarization is remarkably less pronounced in comparison to cases of Cl, Br, and I, the ESP of the covalent fluorine atom in Selectfluor is also distributed anisotropically, which indicates that the covalent fluorine atom of Selectfluor has the possibility to form fluorine bonding. In recent years, covalent fluorine atom as a donor of halogen bond has been frequently reported,⁴⁸ where fluorine atom is attached to strongly electron-withdrawing groups and has a positive σ-hole.⁴⁹ Thus, the fluorine has the ability to act as a halogen bond donor, which has been revealed by statistical analyses of the Cambridge Structural Database and theoretical studies.⁵⁰

Fig. 1 Ab initio molecular electrostatic potential surface (ESP) of Selecfluor at the M06-2X/6-311++G** level (positive potential in blue; negative potential in red). The ESP is mapped on the surface of molecular electron density at 0.001 e a.u.⁻³.

3.2.2 Structural properties and interaction energies. The stable geometries of the π complexes are shown in Fig. 2 and the essential geometric parameters are listed in Table 1. It can be seen that the calculated N–F⋯π and C–H⋯π distances are substantially less than the sum of van der Waals radii of carbon and fluorine or carbon and hydrogen atoms, which indicates the existence of fluorine bonding (N–F⋯π) and hydrogen bonding interactions (C–H⋯π) in the π complexes. It is known that the halogen bonding is highly directional.^45,51 As shown in Table 2, the optimized N1–F⋯π bond angles for all the dimers are around 140° and smaller than other halogen bonds. In addition, the C–H⋯π bond length in the π complexes is slightly shorter than that reported by Houk and Stoddart et al.⁵² These can be rationalized by less polarizable of fluorine as well as the coexistence of F-bond and H-bond in the π complexes.

Fig. 2 The optimized geometries of the π complexes at the M06-2X/6-311++G** level, where (a), (b), (c), and (d) involving fluorobenzene, benzene, toluene and aniline, respectively. Bond distances are given in Å.

Table 2 The geometric parameters of the π complexes N1–F/PhX (X = F, H, CH₃, NH₂) at the M06-2X/6-311++G** level. The bond lengths [d(N1–F), Å], changes of bond lengths [Δd(N1–F), Å], the binding distances [d(F⋯π) and d(H1⋯π) and d(H2⋯π), Å], bond angles (∠N1–F⋯π), and interaction energies corrected with BSSE (ΔE^CP, kcal mol⁻¹)

	–F	–H	–CH3	–NH2
d(N1–F)	1.373	1.373	1.374	1.372
Δd(N1–F)	−0.003	−0.003	−0.001	−0.003
d(F⋯π)	3.188	3.109	3.099	2.934
∠N1–F⋯π	115.7	139.0	142.0	142.6
d(H1⋯π)	3.231	2.660	2.509	2.534
d(H2⋯π)	2.779	2.552	2.634	2.672
ΔE	−8.60	−9.29	−9.45	−12.11
ΔE^CP	−6.60	−7.83	−7.88	−10.34

---

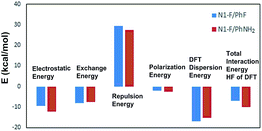
It is well known that, for a given positive site, the strength of halogen bond correlates with the species of halogen bond acceptor. Thus, we supposed that the substituent groups (F, H, CH₃, NH₂) would have pronounced effects on the bonding strength. Indeed, we found that the binding energies of the studied complexes follow the order of electron giving ability of the substituents, that is F < H < CH₃ < NH₂. The binding energies corrected with BSSE span over a broad range from −6.6 to −10.3 kcal mol⁻¹. The most optimal geometry of the π complex is determined by a subtle balance of noncovalent interactions, such as halogen bond and hydrogen bond. Then, we analyze the components of the binding energy by performing the LMO-EDA method. As Fig. 3 shows, it is clear that the dispersion, as well as electrostatic energies play the most important role in stabilizing of the π complexes.

Fig. 3 The energy decomposition analysis of the π complexes of fluorobenzene and aniline with Selectfluor based on the LMO-EDA method.

3.2.3 Population analysis. The energetic stabilization based on donor–acceptor interaction has been evaluated by second-order perturbation energy (E(2)). For these π complexes formed by Selectfluor and substituted benzene, the main contribution to the stabilization is the orbital interactions between the π-electron donor orbital σ(π) of the benzene ring and the N1–F acceptor orbital σ* (N1–F), and the C–H acceptor orbital σ* (C–H). The E(2) related to the H-bond interactions is slightly larger than the F-bond interaction (Table S2†), and the related E(2) values also follow the same trends as bonding energies.

Electronic density analysis by the AIM method suggests the existence of a bond path between the fluorine atom of Selectfluor and the nearest carbon atom in benzene ring, as well as a bond critical point (BCP), which is an important criterion to establish the existence of F-bond. For comparison, the BCP characteristics are summarized in Table 3. According to Rozas et al.,⁵² both F-bond and H-bond here belong to weak interactions with positive values for electron density Laplacian (∇²ρ) and total local energy density (Hc). It should be pointed out that, higher ε value can be obtained at F-bond critical point, which indicates that the electron density is unequally distorted.

Table 3 The electron density (ρ, a.u.), Laplacian of electron density (∇²ρ, a.u.), bond ellipticity (ε) and electron energy density (H, a.u.) at the F⋯C1 and H⋯π bond critical points (BCP) in the π complexes. The BCP of H₁⋯π for N1–F/PhF complex is not observed

Complex	F⋯π				H1⋯π				H2⋯π
	ρ	∇^2ρ	ε	H	ρ	∇^2ρ	ε	H	ρ	∇^2ρ	ε	H
N1–F/PhF	0.0085	0.0339	0.5469	0.0013	—	—	—	—	0.0087	0.0267	2.1940	0.0012
N1–F/PhH	0.0068	0.0265	3.1879	0.0010	0.0075	0.0202	0.0413	0.0008	0.0092	0.0274	0.2256	0.0012
N1–F/PhCH3	0.0069	0.0266	2.6507	0.0010	0.0098	0.0290	0.1629	0.0013	0.0079	0.0220	0.0243	0.0009
N1–F/PhNH2	0.0094	0.0362	1.5946	0.0012	0.0094	0.0273	0.2705	0.0011	0.0079	0.0224	0.2944	0.0010

---

3.3 Fluorination reaction mechanism

The fluorination of aromatic compound with Selectfluor involves an initial formation of an encounter π complex. Then, the fluorine atom or fluorine cation of Selectfluor further approaches and subsequently bonds to the aromatic carbon. This step would weaken the aromaticity of the benzene ring and produce the cationic intermediate (σ complex).⁵³ This σ intermediate is usually an unstable and highly reactive species. Finally, the subsequent proton abstraction recovers the aromaticity and affords the final fluorinated aromatic product (Scheme 2).

The classical interpretation of the fluorinations with N–F reagents is known as the polar S_N2 mechanism. The free energy profile of the fluorination of aniline via the S_N2 mechanism was given as an example (Fig. 4), and those for other PhX (X = F, H, CH₃) were collected in ESI (Fig. S1 and S2†). For aniline, we located two transition state structures for σ-complex formation and proton abstraction, and the formation of the σ-complexes is rate-determining. For other aromatic compounds, only a transition state structure involving σ-complex formation has been located, all attempts to locate a transition state for proton abstraction lead to the final fluorinated aromatic product, which indicates that at the level of theory considered, proton abstraction proceeds without barrier and transition state. Additionally, it can be found that the activation energy barrier (Fig. S1†) is largely dependent upon the substituent groups on the benzene ring. The electron donating group decreases the energy barrier, whereas the electron-withdrawing group (such as F atom) increases it.

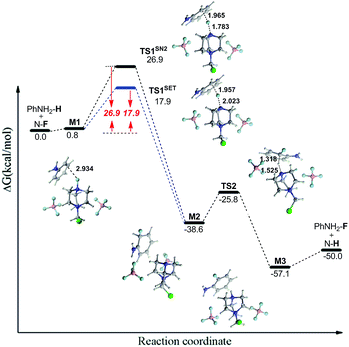Fig. 4 The energy curves of SET and S_N2 mechanisms for the fluorination of aniline with Selectfluor. Bond distances are given in Å.

As an alternate pathway, the SET mechanisms is also suggested to be possible for the formation of σ intermediate. In order to study the SET mechanism, we recomputed the transition states of fluorine transfer from Selectfluor to substituted benzenes with spin-broken wavefunction.⁴² Lower barriers were found for the SET than the S_N2 mechanism (with an energy difference of 4–9 kcal mol⁻¹, list in Table 4), indicating that the SET mechanism is preferred for the fluorination with Selectfluor. Ring substituents have markedly effects on the relative stability of the relevant transient states. Similar with the S_N2 mechanism, the electron donating groups decrease the energy barrier, and the electron-withdrawing group (such as F atom) increases it. To get a fuller picture of the effect of different substituents on the energy barriers, we have studied another six substituted aromatic compounds (see Table 4). The calculations further confirm the above result, and also indicate the stronger the electron-donating ability of the group, the lower energy barrier. The effect of different substituents on the fluorination can be explained by frontier molecular orbital (FMO) theory.⁵⁴ It is known that the values of LUMO/HOMO energy gap reflect the chemical activity of the molecule. The larger the HOMO/LUMO energy gap, the more stable and less reactive the molecule.⁵⁵ Thus, we computed the frontier orbital energies and HOMO/LUMO gaps for the selected substituted benzenes. As shown in Table S3,† the electron-donating groups (NH₂ and CH₃) reduce the HOMO/LUMO gap, and F atom slightly increases the HOMO/LUMO gap, indicating that the electron-donating groups activate the aromatic ring by increasing the electron density on the ring, while the electron-withdrawing group exerts the reverse effect. The results are in agreement with the effects of different substituents on the free energy barriers of the fluorination.

Table 4 The computed free energy barriers for the fluorination of different substituent benzenes involved in the S_N2 and SET mechanisms. Energies are given in kcal mol⁻¹

			TS1^SETgas	TS1^SETsol
Fluorobenzene	44.13	48.51	38.31	43.28
Chlorobenzene	43.06	47.58	37.05	42.11
Benzene	43.77	47.50	38.46	42.96
Toluene	40.69	44.29	35.67	39.95
Mesitylene	33.49	38.57	28.94	34.48
Anisole	32.40	39.17	28.55	35.22
4-Anisaldehyde	37.36	43.31	32.68	38.56
Naphthaline	35.85	40.81	29.53	35.35
Phenol	38.91	42.22	29.91	36.00
Aniline	26.86	32.58	17.89	22.42

---

It is well known that the regioselectivity of an electrophilic aromatic substitution is affected by the substituents on the benzene ring. In order to understand the regioselectivity of the electrophilic aromatic substitution with Selectfluor, the spin density maps (SDM) of odd electron character on the electron density surface of the aromatic ring radical cations were sketched. As shown in Fig. 5, it can be found that the highest spin density is located on both ortho and para positions, indicating that the electrophile (Selectfluor) favours attack at the ortho and para positions, which is consistent with the experimentally observed regioselectivity.⁸ As reported previously, the DABCO moiety of Selectfluor has a great impact upon the reactivity.¹² To gain detailed insight into what happens to the molecules, we discussed the changes of geometrical parameters along the fluorination reaction coordinate. In Fig. 6a, as the N1–F distance elongates, the C–N1 distance shortens at the same rate, which suggests that it was the approach of Selectfluor to the benzene ring that results in the breaking of N1–F bond. In addition, on the extension of the N1–F bond (Fig. 6b), the radius of DABCO moiety cage in Selectfluor, that is N1–N2 distance, reduced by almost 0.1 Å, but increased slightly after fluorine transfer from Selectfluor is complete. Thus, we may say that the DABCO moiety works in stabilization of the transition state structures and takes an active role in the fluorination of aromatic compounds with Selectfluor, although not conclusive. The present results suggest that one may modulate the reactivity of the fluorination reaction by tuning the flexibility of the DABCO moiety.

Fig. 5 Spin density maps of the radical anion of Selectfluor and the radical cations of substituted benzenes calculated at the UM06-2X/6-311++G** level.

Fig. 6 The C–N1 and N1–N2 distances (Å) projected onto the N1–F distance (Å) for the fluorinated reaction of PhX with Selectfluor (X = F, H, CH₃, NH₂).

The solvent effect has been studied using the PCM model with acetonitrile as the solvent. The relative Gibb's energies are collected in Table S4.† It can be found that in acetonitrile the relative free energies of all structures are higher than those in the gas phase, but the overall trend in solvent is similar to that in the gas phase, and in acetonitrile the formation of the σ-complexes is still the rate-limiting step for the fluorination with activation free barriers of 32.6 and 23.2 kcal mol⁻¹ for TS1^S_N2 and TS1^SET, respectively. In addition, it is shown that the free energy difference between TS1^S_N2 and TS1^SET is slightly larger after considering the solvent effects (9.5 vs. 9.0 kcal mol⁻¹). To be prudent, we re-optimized the structures of TS1^S_N2 and TS1^SET by PCM-M06-2X method, and a similar energy barrier of 10.0 kcal mol⁻¹ was obtained. The results indicate that the polarity of the solvent has a consistent effect on the SET and S_N2 processes, and in acetonitrile the SET mechanism is still preferred over the S_N2, which suggests that acetonitrile as a bulk solvent plays a negligible role in controlling the aromatic fluorination with Selectfluor.

3.4 Two-state model analyses of the SET mechanism

To get deep insight into the SET mechanism, a two-state model analysis was addressed, in which we defined substituted benzenes as an electron donor (D) and Selectfluor as an electron acceptor (A). For a reaction between donor D and acceptor A, initial formation of π-complex (M1) can lead to σ-complex (M2) through the fluorine transfer. In this process, the π-complex may be at a charge localized state (DA) where electron transfer is hypothetically deactivated, or a charge transfer state (D⁺A⁻) with completely one electron transfer between monomers. We computed the individual energies of π- and σ-complexes for constrained DA and D⁺A⁻ electronic states by performing a constrained DFT calculations, and obtained the charge localized (DA) and charge transfer (D⁺A⁻) states by minimizing the total energy under an explicit constraint of the electron density.³³ As summarized in Table 5, take benzene/Selectfluor for example, the energy of M1 at DA state is about 162 kcal mol⁻¹ lower than that at the D⁺A⁻ state. This energy corresponds to moving one electron from the benzene to the Selectfluor fragment (about 152.0 kcal mol⁻¹).⁴² Thus, the ground state of π complex is charge localized state (DA). Analogously, the ground state of σ-complex is proved to be charge transfer state (D⁺A⁻).

Table 5 The energy differences (ΔE, kcal mol⁻¹) of the charge transfer (D⁺A⁻) and charge localized (DA) states for π-complex (M1), fluorine transfer transient state (TS1) and σ-complex (M2) involving different substituent benzenes PhX (X = F, H, CH₃, NH₂) calculated by constrained DFT. Energies are given in kcal mol⁻¹

	M1	TS1	M2
–F	185.40	−14.54	−82.00
–H	162.27	−15.02	−89.31
–CH3	179.69	−12.69	−81.84
–NH2	168.39	−36.71	−103.71

---

For the transition state structures of fluorine transfer, we found that the D⁺A⁻ state is more stable by about 10 kcal mol⁻¹ than the DA state, indicating that the D⁺A⁻ state makes greater contribution to the ground state than the DA state. That is to say, the electron transfer and the fluorine transfer may occur successively rather than simultaneously. The transformation from the π-complex to the σ-complex involves two steps. Step I involves one electron transfer from the aromatic substrate (D) to Selectfluor (A). In step II, the collapse of the radical fluorine to the carbon in aromatic ring affords the classical σ intermediate, which undergoes further proton extraction to release the final fluoride aromatic substance.

Furthermore, owing to weak electronic coupling, the SET reaction may be nonadiabatic and involves avoided crossings around the transition state.⁵⁶ Avoided crossing (or interaction) of the two states DA and D⁺A⁻ at the intersection points also a way to look at the source of the SET reaction barrier. The potential energy curves of the DA and D⁺A⁻ states of benzene/Selectfluor along the reaction coordinate is plotted in Fig. 7. For simplicity, the molecular structures along the reaction coordinate is obtained through the IRC calculation, by a steepest descent path in mass-weighted Cartesian coordinates.⁵⁷ As we can see, an energy equality E(DA) = E(D⁺A⁻) is achieved at the crossing point, indicating that at this point the interaction of the two states is the strongest, which pushes the reaction to proceed on the lower energy curve rather than through the crossing point. An avoided crossing interaction (H_ab) could be defined as the difference in the relative energy of the crossing point and the activation barrier.⁵⁸ In this reaction, the relatively large avoided crossing interaction is calculated to be nearly 20 kcal mol⁻¹, indicating that the SET reaction can be described in the usual way using standard transition state theory.

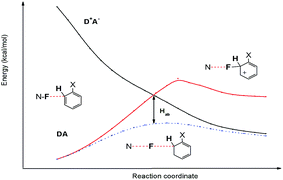Fig. 7 Potential energy curves of the charge transfer (D⁺A⁻) and localized (DA) states, as well as the reaction energy curve of SET mechanism (dotted line) as a function of the reaction coordinate.

4. Conclusions

In summary, a systematic theoretical investigation was performed to understand the fluorination process of aromatic compounds with Selectfluor. Our data confirms that the non-covalent fluorine bond is formed in the π complexes of aromatic compounds and Selectfluor, which works in the stability of the π complexes. In addition, our computation indicates that the SET mechanism is preferred over the S_N2. The energy barrier of the fluorination reaction reduces as the electron donating ability of the substituents increases. Moreover, the potential energy curves of the charge localized diabatic states along the fluorine transfer process provides a direct understanding of the SET process, and suggests that the electron transfer and the fluorine transfer occur successively rather than simultaneously. Due to a relatively large avoided crossing interaction (about 20 kcal mol⁻¹), the SET reaction is adiabatic, and thus it can be described by using transition state theory.

Acknowledgements

This work was supported by National Natural Science Foundation of China (no. 91127014, no. 21433006) and the Provincial Natural Science Foundation of Shandong, China (Grant 2014ZRE27295).

Notes and references

1. R. D. Chambers, Fluorine in Organic Chemistry, Blackwell Publishing Ltd., 2004, pp. 1–22.
2. K. Uneyama, Organofluorine Chemistry, Blackwell, Oxford, 2006, p. 3.
3. R. E. Banks, B. E. Smart, and J. C. Tatlow, Organofluorine Chemistry. Principles and Commercial Applications, Plenum Press, New York, 1994.
4. G. I. Borodkin, P. A. Zaikin, M. M. Shakirov and V. G. Shubin, Russ. J. Org. Chem., 2007, 43, 1451.
5. G. I. Borodkin, P. A. Zaikin and V. G. Shubin, Tetrahedron Lett., 2006, 47, 2639.
6. P. Kralj, M. Zupan and S. Stavber, J. Org. Chem., 2006, 71, 3880.
7. I. Pravst, M. P. Iskra, M. Jereb, M. Zupan and S. Stavber, Tetrahedron, 2006, 62, 4474.
8. R. V. Andreev, G. I. Borodkin and V. G. Shubin, Russ. J. Org. Chem., 2009, 45, 1468.
9. G. I. Borodkin, I. R. Elanov and V. G. Shubin, Russ. J. Org. Chem., 2010, 46, 1317.
10. K. K. Laali and G. I. Borodkin, J. Chem. Soc., Perkin Trans. 2, 2002, 953.
11. S. Stavber and M. Zupan, Acta Chim. Slov., 2005, 52, 13.
12. P. T. Nyffeler, S. G. Durón, M. D. Burkart, S. P. Vincent and C. Wong, Angew. Chem., Int. Ed., 2005, 44, 192.
13. S. D. Taylor, C. C. Kotoris and G. Hum, Tetrahedron, 1999, 55, 12431.
14. S. P. Vincent, M. D. Burkart, C.-Y. Tsai, Z. Zhang and C.-H. Wong, J. Org. Chem., 1999, 64, 5264.
15. E. Differding and G. M. Rüegg, Tetrahedron Lett., 1991, 32, 3815.
16. E. Differring and M. Wehrli, Tetrahedron Lett., 1991, 32, 3819.
17. X. Zhang, Y. Liao, R. Qian, H. Wang and Y. Guo, Org. Lett., 2005, 7, 3877.
18. J. K. Kochi, Acc. Chem. Res., 1992, 25, 39.
19. E. K. Kim, T. M. Bockman and J. K. Kochi, J. Am. Chem. Soc., 1993, 115, 3091.
20. J. F. d. Queiroz, J. W. d. M. Carneiro, A. A. Sabino, R. Sparrapan, M. N. Eberlin and P. M. Esteves, J. Org. Chem., 2006, 71, 6192.
21. X. Zhang, J. Mol. Struct., 2013, 1050, 21.
22. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
23. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
24. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
25. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, 1995.
26. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
27. V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma and V. G. Zakrzewski, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford CT, 2010.
29. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9.
30. K. A. Todd, AIMAll (Version 12.05.09), TK Gristmill Software, Overland Park KS, USA, 2012.
31. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
32. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
33. Q. Wu and T. Van Voorhis, J. Chem. Phys., 2006, 125, 164105.
34. J. C. Katharine and P. J. Richard, J. Org. Chem., 2013, 78, 1864.
35. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477.
36. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
37. J. F. Dobson, G. Vignale and M. P. Das, Electronic Density Functional Theory: Recent Progress and New Directions, Plenum, New York, 1998.
38. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
39. X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673.
40. S. Grimme, J. Chem. Phys., 2006, 124, 1.
41. O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109.
42. Y. A. Serguchev, M. V. Ponomarenko, L. F. Lourie and A. A. Fokin, J. Phys. Org. Chem., 2011, 24, 407.
43. D. Lenoir, Angew. Chem., Int. Ed., 2003, 42, 854.
44. T. Clark, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 13.
45. T. Clark, M. Hennemann, J. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291.
46. A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686.
47. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748.
48. Y. Lu, J. Zou, Q. Yu, Y. Jiang and W. Zhao, Chem. Phys. Lett., 2007, 449, 6.
49. P. Metrangolo, J. S. Murray, T. Pilati, P. Politzer, G. Resnati and G. Terraneo, Cryst. Growth Des., 2011, 11, 4238.
50. A. G. Dikundwar and T. N. G. Row, Cryst. Growth Des., 2012, 12, 1713.
51. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154.
52. A. R. Williams, B. H. Northrop, K. N. Houk, J. F. Stoddart and D. J. Williams, Chem.–Eur. J., 2004, 10, 5406.
53. R. B. Dawson and J. R. Escritt, Nature, 1946, 158, 448.
54. M. Shravani, S. Balaiah, K. Srinivas, K. Bhanuprakash and I. Huc, ChemPhysChem, 2012, 13, 3526.
55. M. A. Migahed, A. M. Al-Sabagh, E. A. Khamis, M. A. Raouf and E. G. Zaki, Chem. Mater. Res., 2014, 6, 46.
56. D. R. Yarkony, J. Phys. Chem., 1996, 100, 18612.
57. K. Fukui, S. Kato and H. Fujimoto, J. Am. Chem. Soc., 1975, 97, 1.
58. Y. Xing, X. Xu, L. Chen, Z. Cai, X. Zhao and J. Cheng, Phys. Chem. Chem. Phys., 2002, 4, 4669.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra15202f

---