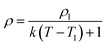Numerical study of melted PCM inside a horizontal annulus with threads in a three-dimensional model

Abstract

This paper presents a numerical investigation of the melting process of a phase change material (PCM) in a tube and shell geometry. Since previous literature mainly focused on the 2-D model, a 3-D model is established in the present work with CFD software to take the velocity and heat transfer along the axial direction into account. In order to enhance the tube's heat transfer performance, two types of threads with different geometry parameters are introduced. The inner cylinder is assumed to be at constant temperature and the outer cylinder insulated. Temperature contours and streamlines are obtained to cast light on the effect of the threads. The predicted result shows all the threads can accelerate the melting process in the top region where natural convection is dominant, and the magnitude of the enhancement is determined by geometry parameters to some extent. However, none of the applied threads has improved the melting rate at the bottom region where heat conduction is dominant.

---

1. Introduction

Over the last three decades, the thermal energy storage of phase-change materials (PCMs) has been intensively studied by numerous researchers because of their high thermal energy densities per unit volume/mass and their potential for applications in different engineering fields with wide temperatures ranges. PCM thermal energy storage is critical for eliminating the discrepancy between energy supply and demand as well as for improving the efficiency of solar energy systems.¹ Latent heat storage devices, which utilize phase change, are capable of providing high energy storage density while maintaining a relatively constant temperature during charging/discharging, making them a particularly attractive type of thermal storage system.² PCMs are used in different engineering fields, such as in the following: the thermal storage of building structures; building equipment, including domestic hot water; heating and cooling system, electronic products, drying technology, waste heat recovery, refrigeration and cold storage, solar air collectors, and solar cookers.³

Assis et al.⁴ investigated both numerically and experimentally on melting in a spherical shell. They performed their numerical studies using the commercial software Fluent 6.0. Computational results had a good agreement with experimental results for different wall temperatures and different shell diameters. Khillarkar et al.⁵ numerically investigated the melting process of a pure PCM in tube geometry of two various configurations (square external tube with a circular tube inside and circular external tube with a square tube inside). Thermal stratification was observed in the upper section of the cavity because of the natural convection. Ng et al.⁶ carried out a numerical simulation of convection melting of a PCM in a cylindrical annulus heated isothermally from the inside wall. The impact of Rayleigh number on the melting rate as well as the evolution of the fluid flow pattern was investigated. It was found that enhancement in Rayleigh number increased heat transfer rate. Also, melting of PCM in the bottom section was very ineffective because the energy modified to the system was mostly transferred to the upper section.

In terms of the PCMs, they are generally divided into three main categories, organic PCMs, inorganic PCMs and eutectics of organic and inorganic compounds.^7–9 Paraffinic PCMs have been used by many researches¹⁰ as a thermal storage material. One of the major reasons of using paraffin PCM is their very little or no sub-cooling and non-corrosive nature. Inorganic PCMs in general have a rather high heat of fusion and good thermal conductivity. These are cheap and non-flammable also compared to paraffin PCMs. However, most of them are corrosive to metals and undergo sub-cooling process. Sharma A. et al.^11,12 presented the eutectic materials as novel PCMs of thermal storage system applications in buildings. They prepared eutectics PCMs with different weight percentages. Based on their measurements, they found if CA (capric acid) mixed with any other lower melting temperature PCM than a desired eutectic can be developed for the building applications. Also, the thermal properties of binary mixtures measured by using the DSC technique showed that several developed materials have proper phase change temperature and high latent heat of fusion. To sum up, according to the work of Zalba et al.,¹³ the organic materials have some advantages over the inorganic ones: no corrosives, low or none undercool and chemical and thermal stability. However, the organic materials have disadvantages as well: lower phase change enthalpy and low thermal conductivity, and over 150 materials used in research as PCMs and about 45 commercially available PCMs are listed in their work.

Considerable researches have been done to explore the effect of various container geometries on latent heat thermal storage performance. Among the container geometries, latent heat thermal storage systems with shell and tube design are the most prevalent one, accounting for more than 70%.² Meanwhile, cylindrical geometry is considered most promising for devices of commercial heat exchangers, such as the double-pipe heat exchanger and shell and the tube heat exchanger, because of their high-efficiency in a minimum volume. Most researchers use this geometry, filling the PCM in the tube side or in the annulus (shell). Commercial products of PCMs are delivered in these geometries.³ However, due to the low thermal conductivity possessed by most phase change materials, heat transfer enhancement technique is required to improve charging/discharging rate of the latent heat thermal storage system.¹⁴ One of these techniques is to apply an optimized geometry for the PCM container.¹⁵ On the other hand, several researchers investigated heat transfer enhancement in PCMs using various techniques such as the use of finned tubes, insertion of a metal matrix in the PCM, multi-tube, bubble agitation in PCM, PCM dispersed with high-conductivity particles and multiple families of PCMs in LHTE. Various fin configurations are applied to PCM, including external and internal fin (circular, longitude, and rectangular).¹⁶ Velraj et al.¹⁷ have reviewed the attempts that have been made on heat transfer enhancement. They also tested different methods of heat transfer enhancement, which included the use of longitudinal internal finned tubes in a shell and tube heat storage unit, dispersing the PCM with high thermal conductivity particles and using metallic packing, such as Leasing rings, placed inside the tubes contain the PCM. Reddy¹⁸ modeled a PCM–water solar system consisting of a double rectangular cross section enclosure where the top enclosure is filled with paraffin wax and the bottom is filled with water. The numerical modeling has been carried out using the commercial CFD software Fluent. The geometry modeling and mesh were generated in GAMBIT. The results of simulation indicate that an optimal number of fins should be used to optimize the overall system performance. Ismail et al.¹⁹ studied PCM solidification inside a typical shell and tube container. The heat transfer fluid flowed inside the tubes and the PCM was filled in the shell around the tubes. The effects of varying Reynolds and Stefan numbers, different phase change temperatures, system length and outer radius of fusion for the tubes were studied. They showed that only the phase change temperature was insignificant to system performance, all other investigated parameters had significant impact. Hamada et al.²⁰ studied experimentally the effects of carbon fiber chips and the carbon brushes, as additives, on the heat transfer rate in the PCM for a shell and tube type apparatus. The investigated apparatus had four identical tubes arranged asymmetrically. Agyenim et al.¹⁵ made a comparison between two container geometries: a concentric annulus and a shell with four identical heat transfer tube. Their experimental results showed that the heat transfer rate during charging was improved using multi-tube in place of the single tube. By comparing the temperature gradients in the axial, radial and angular directions, they verified the validity of ignoring thermal conductivity in the direction parallel to the heat transfer fluids, and thus validating the representation of a cylindrical container two-dimensionally. Huawei Liu et al.²¹ proposed a hierarchical tube array design inside the shell. The tubes are designed non-uniformly both in terms of arrangement and in terms of size, following the general concept of “few large and many small”. Balikowski and Mollendorf²² studied the effect of using a spinned pipe tube and smooth pipe heat exchanger with two types of PCMs on the charging/discharging of a vertical double pipe heat exchanger with different PCMs in the annular gap. Agyenim et al.²³ used circular and longitudinal fins to enhance heat transfer. They found that the longitudinal-finned system is suitable for charging and discharging in a concentric tube PCM system because such system can achieve optimal charge performance with negligible sub-cooling during discharge. Erek et al.²⁴ investigated the behavior of thermal energy storage (shell and tube type) with a circular-finned tube and PCM in annular space. They developed a two-dimensional numerical model to predict the effect of fin and operation parameters (fin space, fin diameter, Re number, and heat transfer fluid inlet temperature) on the solidification and melting processes of PCM. Mesalhy et al.²⁵ performed a numerical study for increasing the thermal conductivity of PCM using porous matrix in two concentric cylinders. They found that the presence of porous matrix had effect on the melting rate of PCM while it damped the convection motion. In this way, the decreases of the porosity enhanced the melting rate. Ahmad Ali²⁶ presented numerical study of melting between two cylinders for concentric and eccentric state. This study was done to investigate the effect of position of inner cylindrical tube on melting of PCM (charging) in outer cylindrical shell.

The Fluent software by ANSYS is a computational fluid dynamic (CFD) program used successfully to simulate different engineering problems. This software has a specific model that can simulate a range of different melting and solidification problems in engineering, including casting, melting, crystal growth, and solidification. The program can be used to solve the phase change that occurs at a single temperature (pure metals) or over a range of temperatures (mixture, alloy). The applications and limitations of Fluent can be found in ref. 27. Hosseinizadeh et al.²⁸ numerically studied the effect of various volume fractions of nanoparticle copper on an unconstrained melting rate in a spherical container. Different volumes of nanoparticle copper (0, 0.02, 0.04) per volume were used, and 85% of the PCM was filled. They used Fluent to develop an axis-symmetric numerical model and added the Darcy law to the momentum equation to account for the effect of phase change on convection. Tan et al.²⁹ reported an experimental and numerical work on the constrained melting of PCM inside a transparent spherical glass capsule. The Darcy law was added to the momentum equation to account for the effect of phase change on convection. They used Fluent 6.2.16 for the numerical simulation and the simple method for solving the governing equations. The power law differencing scheme was used to solve the momentum and energy equations, whereas the PRESTO scheme was adopted for the pressure correction equation. Arasu and Mujumdar³⁰ presented a numerical investigation on the melting of paraffin wax dispersed with aluminum (Al₂O₃) as nano-PCM in a square enclosure heated from the bottom side and from a vertical side with different volume percentages (2% and 5%). They developed a numerical model using Fluent 6.3.26. The computational domain was resolved with a fine mesh near the hot and cold wall to resolve the boundary layer, and an increasingly coarse mesh was used in the rest of the domain to reduce computational time. They used a UDF to define the temperature-dependence of the thermo-physical properties of PCM. They reported that the effective thermal conductivity of a paraffin wax latent heat storage medium could be increased significantly by smaller volumetric concentrations of alumina particles in the paraffin wax. The CFD software is successively used to simulate the application of PCMs in different engineering applications and using CFD software to design LHTES is believed to be an effective way to save money and time.⁶

However, in the tube and shell geometry, most previous literatures using CFD software (Fluent) mainly focused on 2D-model, ignoring the molten PCM velocities along the axial direction, which may have influence on the melting time. This paper presents a numerical study of melting between two concentric cylinders with a 3-D mode: the inner cylinders with thread and the outer cylinder plain, taking the velocities along the axial direction into account. The inner cylinder with thread is assumed constant temperature and the outer cylinder insulated. Two types of threads and different geometry parameters are considered in present investigation. During the melting process, the effect of the thread on the temperature distribution, streamline is investigated.

2. Governing equations

Given the complexity of the constrained melting of PCM, some pertinent assumptions made are listed below:

(1) Both the liquid and solid PCM are isotropic and homogeneous, thus their thermo-physical properties are considered constant.

(2) At the liquid–solid interface, thermal equilibrium is reached.

(3) Boussinesq approximation: the density change within the liquid phase that drives natural convection is only considered in the body force terms.

Density variation is defined as:

where ρ_l is the density of PCM at the melting temperature at T_l, and k is the thermal expansion coefficient.

(4) Viscous dissipation is considered negligible due to low velocity.

Based on these assumptions, the present numerical study is considered transient, laminar, incompressible and 3-D, without viscous dissipation. Thermo-physical characteristics of the PCM such as the specific heat, thermal conductivity, and viscosity are given as constant in the analysis.

We use the finite volume method for computation. The melting process is simulated using an enthalpy-porosity technique, where a quantity called the liquid fraction, noted as γ, is used to indicate the melt fraction (MF) of a cell volume. As the PCM melts, γ increases from 0 to 1. PCM between the solidus and liquidus temperature is in a so-called mushy state. In the mushy zone, material property transformation of the phase-changing PCM is assumed to be linear. The mushy zone is modeled as a “pseudo” porous medium whose porosity equals γ. The governing conservation equations are the continuity equation, the momentum equation and the energy equation:

∂_t(ρ) + ∂_i(ρu_i) = 0 (1)

∂_t(ρu_i) + ∂_j(ρu_iu_j) = μ∂_jju_i − ∂_ip + ρg_i + S_i (2)

∂_t(ρh) + ∂_t(ρΔH) + ∂_i(ρu_ih) = ∂_i(β∂_iT) (3)

where h is the sensible enthalpy of the PCM, T is the temperature, ρ is density of the PCM, β is the thermal conductivity of PCM, u_i is the velocity and S_i is volumetric heat source term and is equal to zero in the present study.

The enthalpy of the material H is computed as the sum of the sensible enthalpy h, and the latent heat, ΔH.

H = h + ΔH (4)

Where h can be expressed as follows:where h_ref is the reference enthalpy at the reference temperature T_ref, and C_p is the specific heat.

ΔH = γL (6)

where L is the latent heat of fusion of the PCM, and γ is liquid fraction and is defined as:

The source term S_i in momentum equation, is defined as

where is the “porosity function” defined by Brent et al.³¹ that enables the momentum equations to “mimic” Carman–Kozeny equations for flow in porous media. C is the constant reflection of the mushy zone morphology. C describes how steeply the velocity is reduced to zero when the material solidifies. This constant varies between 10⁴ and 10⁷ (10⁵ is applied in this paper).³² ε is a small number (0.001) to prevent division by zero.

3. Numerical procedure

Numerical study of the present problem is solved using the CFD software, FLUENT 14.0. The original model is shown in the Fig. 1, flat inner cylinder and flat outer cylinder, which is simulated to verify the correctness of our model.

Fig. 1 Scheme of the original 3-D model.

The organic material used in our stimulation is Eicosane (alternative spelling Icosane), an alkane with the chemical formula C₂₀H₄₂. It has little use in the petrochemical industry, as its high flash point makes it an inefficient fuel. However, its moderate phase transition temperature makes it a candidate for PCM, which can be used to store thermal energy and control temperature and suggested as one of the most promising group of PCM according to Sharma A et al.³³ The thermo-physical properties are listed in Table 1.

Table 1 Thermo-physical properties of PCM

Properties	Symbol	Values
Melting temperature	Tliquidus–solidus	35–37 °C
Density	ρ	770 kg m^−3
Kinematic viscosity	μ	5 × 10^−6 m^2 s^−1
Specific heat	cp	2460 J kg^−1 K^−1
Thermal conductivity	β	0.1505 W m^−1 K^−1
Latent heat of fusion	L	247.6 kJ kg^−1
Thermal expansion coefficient	k	0.0009 K^−1

---

The inner cylinder's and outer cylinder's diameters are 20 mm and 40 mm, respectively. The inner tube is made of copper with a constant thermal conductivity of 400(W m⁻¹ K⁻¹), and the shell consists of copper and heat insulating material-PE, which is short for polyethylene. The length along the axial direction is 2 mm in order to investigate whether the axial velocity of molten PCM has effect on the temperature distribution, therefore influencing the melting time.

The actual heat transfer process is: hot water or other working medium flows inside the tube, and heat is abstracted from the working medium into the copper (in this paper). After a process of heat conduction in the metal, the PCM gains heat and begins to melt. However, in the overall heat transfer process, the convective heat transfer coefficient between the working medium and tube is very huge. And the thermal resistance of the metal is very small due to high thermal conductivity the copper possesses. If we neglect the temperature difference along the axial direction, the simplification that the tube possesses the temperature of the working medium is valid. In terms of the shell, heat can hardly escape from the system due to very low thermal conductivity of the heating insulating material. Thus this assumption should be valid as well.

Based on simplification and assumption above, the boundary conditions are set as follows:

The inner cylinder is considered possessing a constant temperature, 329.15 K, while the outer cylinder is considered insulated. At the beginning of the simulation, the temperature is distributed uniformly with a sub-cooling of 1 K. The comparison of present circumstance and the work of Assis⁴ is shown in Fig. 2. It can be figured out that the present model agreed well with the precedent work.

Fig. 2 Comparison of liquid fraction versus time between present study and Assis et al.⁴ work.

We used second order upwind scheme to solve the momentum and energy equations, and the PISO method for pressure–velocity coupling are used. Also the PRESTO scheme is adopted for the pressure correction equation. The under-relaxation factors for the pressure, density, body force momentum, liquid fraction update and energy are 0.3, 1, 1, 0.7, 1, respectively. The number of the grid is increasing rapidly and time-consuming as the model is turned to three-dimensional. Thus, only one grid size and a certain time step (0.001 s) were selected to do the simulations. However, all the error of the calculated result is limited in the simulation process. The number of iterations for every time step is fixed at 40, which is sufficient to satisfy the convergence criteria (10⁻³).

As shown in Fig. 3, it can be obviously seen the existence of the velocity along the Z axis (axial direction). However, the turbulence made little difference in the melting condition and melting time, since the axial velocity is relatively small compared to the velocity along X and Y (one to two order of magnitude), which also proves the 2-D simplification is adequate in such circumstances where the inner cylinders are plain. While such 2-D models can hardly be applied to other devices with apparatuses, for instance, threads and fins, which aim to promote a flow of heat and mass transfer in axial direction.

Fig. 3 Streamline captured at 180 s of the melting process at cross section.

It's known that there are two methods to improve the tube's heat transfer performance, one is expanding the efficient surface, namely rolling the tube into different surface, such as fin and threads which can bring about turbulent flow field, and another is to improve the performance of the tube's surface, such as porous surfaces which can promote coefficient of heat transfer in boiling condition to great extent.³⁴ In order to accelerate the melting rate of PCM, in present study, different types of thread are used to cause turbulence in the flow field, which can promote the heat transfer performance.

The model used to study the effect of the thread is shown in the Fig. 4.

Fig. 4 Scheme of the 3-D model with tri-angular thread.

The geometry parameters are as same as the model above except for the axial length. The axial length here is taken as the length of the pitch of the screw thread 10 mm, and the thread length is 2 mm and thread height is 0.8 mm, which is represented by 2-0.8 for convenience. The meshing of all these models is refined at the inner cylinders to describe the thread's geometry structure and the boundary layer for obtaining a more accurate outcome.

4. Results and discussion

Instantaneous colored contours of temperature at different time (60 s, 120 s, 180 s, 240 s, 360 s) are presented for plain cylinder and cylinder with 2-0.8 tri-angular thread in Fig. 5.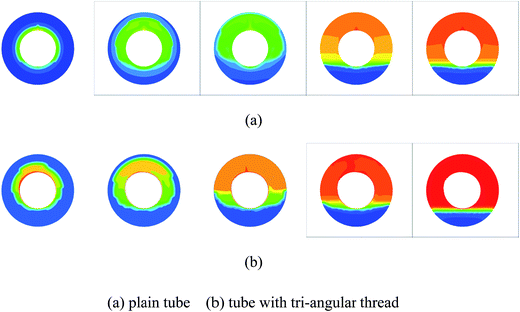

Fig. 5 Temperature contours of plain tube and tube with tri-angular thread (2-0.8) after 60 s, 120 s, 180 s, 240 s, 360 s.

In the tube without thread, it can be seen, at the beginning of the melting process (60 s), very thin melting layer is forming symmetrically. After 60 s, the layer began to expand asymmetrically, resulting in the shape and size of the liquid zone: PCM is more melted in the top region than the bottom region. This phenomenon is due to the effect of natural convection in the top region where warm liquid rises to the top region and cooler liquid replaces.¹ It is the natural convection of the top region that accelerates the melting rate until the time around 360 s. However, the natural convection has no effect on the melting rate when the solid PCM of the top region is almost melted. Therefore, the melting of solid PCM at bottom region, where the dominant heat transfer is heat conduction, is not influenced the natural convection above. And it can explain why the rate of melting is gradually decreasing when the liquid fraction is close to 1.

However, in the tube with thread (2-0.8) in the inner cylinder, the beginning of the melting process (60 s) shows asymmetrical. It is mainly because the initial heat conduction process is asymmetrical due to the added heated surface of thread. As time processes further, the shape of the liquid zone has shown great difference with the shape of the tube without thread: a more asymmetrical shape and greater melting rate. The result is due to the increase of heated surface and enhanced axial direction velocities caused by threads, leading to a more turbulent flow field which can greatly promote heat transfer. After the time of 240 s, the solid PCM of top region is almost melt, thus the melting process is governed by heat conduction in the bottom region. Therefore, in the liquid fraction versus time figure (Fig. 6), the two curves begin to converge.

Fig. 6 Comparison of liquid fraction versus time between plain tube and one with 2-0.8 thread.

To investigate the flow field of the tube with cylinder of thread, the streamlines were captured at 180 s when the natural convection is dominant in the melting process.

It can be observed in Fig. 7 that, because of the existence of the thread, the streamlines at the top and middle region of the tube have formed several recirculation regions, where hot melting liquid not only moves along radial direction, but also axial direction, which lead to mass and heat enhancement. It should be noted that the main recirculation region in the top region is created by some small recirculation ones which can be seen at earlier time. It agreed well with the predicted temperature contour shown above. However, the enhancement of mass and heat does not reach the bottom region, the dominant heat transfer is still heat conduction, which can also be verified by the figure of liquid fraction versus time.

Fig. 7 Streamline captured at 180 s (a) side view of the model (b) vertical view of the model.

In order to investigate the role the geometry of the tri-angular thread, thread length and thread height, two sets geometries of different parameters: 3-1.2, 4-1.6 are applied respectively. The boundary condition and initial condition remains the same as the case of 2-0.8, and the curves of the liquid fraction versus time of each are obtained and compared in Fig. 8.

Fig. 8 Comparison of liquid fraction versus time among different tri-angular threads.

It can be seen the increase of the geometry parameter has limited influence on the natural convection and little effect on the melting process overall. It can be partially explained that as the height and side length increases, the heated surface increases as well, resulting in a limited effect on the melting process, whereas such change does not have influence on the melting process in the bottom region where heat conduction takes the lead.

Then the rectangular thread is also investigated with geometry parameters of length of 2 mm, 3 mm, 4 mm and height of 0.8 mm, 1.2 mm, 1.6 mm respectively. The curves of liquid fraction versus time are shown in Fig. 9.

Fig. 9 Comparison of liquid fraction versus time among different rectangular threads.

It demonstrated that the thread in rectangular shape can also promote the natural convection of the top region to some extent, but does not have influence on the bottom region. Meanwhile, the change in the geometry applied has limited effect on the melting rate.

5. Conclusions

In present study, a 3-D model was established to investigate the role the inner cylinder's threads play in the melting process of the PCM melting in the tube and shell geometry. In the plain tube circumstance, the predicted result of 3-D model agreed well with experimental results, capturing the phenomenon: primary heat conduction in all region, then heat convection and conduction become dominant in top and bottom region respectively, verifying the correctness of the 3-D model.

In the tube with threads circumstance, both tri-angular thread and rectangular thread are predicted to cause flow turbulence and innegligible velocity along axial direction, resulting in the enhancement of the heat transfer performance in the top region, but has limited effect on melting of the bottom region where heat conduction is dominant. Predicted results also indicated that different geometry parameters applied of both types of threads has limited influence on the melting rate generally.

Nomenclature

C	Mushy zone constant, (kg m^−3 s^−1)
cp	Specific heat capacity, (J kg ^−1 K ^−1)
g	Acceleration of gravity, (m s^−2)
h	Sensible enthalpy, (J kg^−1)
href	Reference enthalpy at the reference temperature Tref, (J kg^−1)
H	Total enthalpy, (J kg^−1)
L	Latent heat of fusion, (J kg^−1)
Si	Darcy's law damping term
t	Time, (s)
T	Temperature, (K)
Tref	Reference temperature, (K)
uj	Velocity, (m s^−1)
k	Thermal expansion coefficient, (K^−1)

Greek letters

γ	Liquid fraction
[small tau, Greek, vector]	Shearing force, (Pa)
μ	Viscosity, (Pa s)
ρ	Density of PCM, (kg m^−3)
β	Thermal conductivity of PCM, (W m^−1 K^−1)
ε	A small number (0.001) to prevent division by zero

Subscripts

Liquidus	Liquid
Ref	Reference
Solidus	Solid

References

1. A. A. Al-abidi, S. Bin Mat, K. Sopian, M. Y. Sulaiman and C. H. Lim, A Review of thermal energy storage for air conditioning systems, Renewable Sustainable Energy Rev., 2012, 16, 5802–5819.
2. F. Agyenim, A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS), Renewable Sustainable Energy Rev., 2010, 14(2), 615–628.
3. A. A. Al-abidi and S. Bin Mat, CFD applications for latent heat thermal energy storage: a review, Renewable Sustainable Energy Rev., 2013, 20, 353–363.
4. E. Assis, L. Katsman, G. Ziskind and R. Letan, Numerical and experimental study of melting in a spherical shell, Int, J. Heat Mass Transfer, 2007, 50, 1790–1804.
5. D. B. Khillarkar, Z. X. Gong and A. S. Mujumdar, Melting of a phase change material in concentric horizontal annuli of arbitrary cross-section, Appl. Therm. Eng., 2000, 20, 893–912.
6. K. W. Ng, Z. X. Gong and A. S. Mujumdar, Heat transfer in free convection-dominated melting of phase change material in horizontal annulus, Int Comm., Heat Mass Transfer, 1998, 25(5), 631–640.
7. A. Abhat, Low temperature latent heat thermal energy storage heat storage materials, Sol. Energy, 1983, 30.
8. B. Zalba, J. M. Marin, L. F. Cabeza and H. Mehling, Review on thermal energy storage with phase change materials, heat transfer analysis and applications, Appl. Therm. Eng., 2003, 3, 251–283.
9. A. Khudhair and M. Farid, A review on energy conservation in building applications with thermal storage by latent heat using phase change materials, Energy Convers. Manage., 2004, 45, 263–275.
10. J. Marin, B. Zalba, F. Cabeza and H. Mehling, Free-cooling of buildings with phase change materials, Int. J. Refrig., 2004, 27, 839–849.
11. A. Sharma, A. Shukla, C. R. Chen and T.-N. Wu, Development of phase change materials (PCMs) for low temperature energy storage applications, Sustainable Energy Technologies and Assessments, 2014, 7, 17–21.
12. A. Sharma, A. Shukla, C. R. Chen and S. Dwivedia, Development of phase change materials for building applications, Energ. Build., 2013, 64, 403–407.
13. B. Zalba, J. M. Mar and L. F. Cabeza, Harald Mehling, Review on thermal energy storage with phase change: materials, heat transfer analysis and applications Applied, Therm. Eng., 2003, 23, 251–283.
14. M. M. Farid, A. M. Khudhai, S. A. K. Razack and S. Al-Hallaj, A review on phase change energy storage: materials and applications, Energy Convers. Manage., 2004, 45, 1597–1615.
15. F. Agyenim, P. Eames and M. Smyth, Heat transfer enhancement in medium temperature thermal energy storage system using a multi-tube heat transfer array, Renewable Energy, 2010, 35(1), 198–207.
16. S. Mat and A. A. Al-abidi, Enhance heat transfer for PCM melting in triplex tube with internal-external fins, Energy Convers. Manage., 2013, 74, 223–236.
17. R. Velraj, R. V. Seeniraj, B. Hafner, C. Faber and K. Schwarzer, Experimental analysis and numerical modeling of inward solidification on a finned vertical tube for a latent heat storage unit, Sol. Energy, 1997, 60, 281–290.
18. K. S. Reddy, Thermal modeling of PCM-based solar integrated collector storage water heating system, J. Sol. Energy Eng., 2007, 129, 458–464.
19. K. A. R. Ismail and M. M. Abugderah, Performance of a thermal storage system of the vertical tube type, Energy Convers. Manage., 2000, 41(11), 1115–1190.
20. Y. Hamada, W. Ohtsu and J. Fukai, Thermal response in thermal energy storage material around heat transfer tubes: effect of additives on heat transfer rates, Sol. Energy, 2003, 75(4), 317–328.
21. H. Li, S. Li and Y. Chen, The melting of phase change material in a cylinder shell with hierarchical heat sink array, Appl. Therm. Eng., 2014, 73, 973–981.
22. J. R. Balikowski and J. C. Mollendorf, Performance of phase change materials in a horizontal annulus of a double-pipe heat exchanger in a water-circulating loop, J. Heat Transfer, 2007, 129, 265–272.
23. F. Agyenim, P. Eames and M. Smyth, Experimental study on the melting and solidification behavior of a medium temperature phase change storage material (erythritol) system augmented with fins to power a LiBr–H₂O absorption cooling system, Renewable Energy, 2011, 36, 108–117.
24. A. Erek, Z. Ilken and M. A. Acar, Experimental and numerical investigation of thermal energy storage with a finned tube, Int. J. Energy Res., 2005, 29, 283–301.
25. O. Mesalhy, K. Lafdi, A. Elgafy and K. Bowman, Numerical study for enhancing the thermal conductivity of the phase change material (PCM) storage using high thermal conductivity porous matrix, Energy Convers. Manage., 2005, 46, 847–867.
26. A. Ali Rabienataj Darzi, M. Farhadi and K. Sedighi, Numerical study of melting inside concentric and eccentric horizontal annulus, Appl. Math. Model., 2012, 36, 4080–4086.
27. FLUENT 6.3 User's Guide, Fluent Inc., Lebanon, 2006.
28. S. F. Hosseinizadeh, A. A. R. Darzi and F. L. Tan, Numerical investigations of unconstrained melting of nano-enhanced phase change material (NEPCM) inside a spherical container, Int. J. Therm. Sci., 2012, 51, 77–83.
29. F. L. Tan, S. F. Hosseinizadeh, J. M. Khodadadi and L. Fan, Experimental and computational study of constrained melting of phase change materials (PCM) inside a spherical capsule, Int. J. Heat Mass Transfer, 2009, 52, 3464–3472.
30. A. V. Arasu and A. S. Mujumdar, Numerical study on melting of paraffin wax with Al₂O₃ in a square enclosure, Int. Commun. Heat Mass Transfer, 2012, 39, 8–16.
31. A. D. Brent, V. R. Voller and K. J. Reid, Enthalpy-porosity technique for melting convection-diffusion phase change: application to the melting of a pure metal, Numer. Heat Transfer, 1988, 13, 297–318.
32. W.-B. Ye, D.-S. Zhu and N. Wang, Numerical simulation on phase-change thermal storage/release in a plate-fin unit, Appl. Therm. Eng., 2011, 31, 3871–3884.
33. A. Sharma, V. V. Tyagi, C. R. Chen and D. Buddhi, Review on thermal energy storage with phase change materials and applications, Renewable Sustainable Energy Rev., 2009, 13, 318–345.
34. C. Lixin and C. Tingkuan, Study of vapor liquid two-phase frictional pressure drop in a vertical heated spirally internally ribbed tube, Chem. Eng., 2007, 3, 783–792.

---