DFT and two-dimensional correlation analysis for evaluating the oxygen defect mechanism of low-density 4f (or 5f) elements interacting with Ca-Mt

Abstract

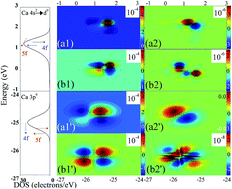
Understanding how f-shell electrons affect clay minerals is important in an ideal buffer/backfill material. Hitherto, however, there have been few reports that quantitatively simulated the effects of low-density 4f (or 5f) electrons on oxygen defects. Here, we used density functional theory (DFT) and two-dimensional correlation analysis (2D-CA) techniques to calculate the origins of the oxygen defect and electronic transitions of f-shell electrons/Ca type montmorillonite (Ca-Mt) system. We determined the number effect of f-shell electrons to explain the oxygen defects of aluminium–oxygen octahedron and silicon–oxygen tetrahedron at the valence band, which is consistent with the orbital fluctuation results. This study offers a new method for explaining the oxygen defect mechanism.