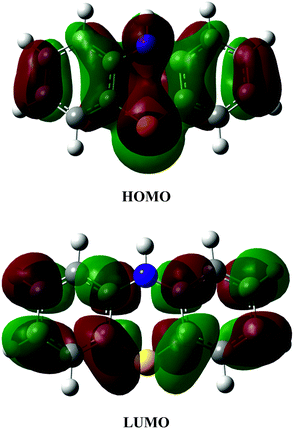Antioxidant vs. prooxidant action of phenothiazine in a biological environment in the presence of hydroxyl and hydroperoxyl radicals: a quantum chemistry study
C. Iuga*a,
A. Camperob and
A. Vivier-Bungeb
aDepartamento de Sistemas Biológicos, Universidad Autónoma Metropolitana-Xochimilco, Calzada del Hueso 1100, 04960 México, D. F., México. E-mail: ciuga@xanum.uam.mx
bDepartamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco No. 186, 09340 México, D. F., México
First published on 19th January 2015
Abstract
In this work, we have carried out a quantum chemistry and computational kinetics study on the reactivity of phenothiazine (PTZ) towards hydroxyl (˙OH) and hydroperoxyl (˙OOH) free radicals, in order to elucidate the antioxidant activity of phenothiazine in biological environments. We investigated three types of reaction mechanisms: (i) single electron transfer (SET), (ii) hydrogen atom transfer (HAT) and (iii) radical adduct formation (RAF). In order to mimic biological environments, we have considered both water and lipid media. We show that, in aqueous solution, PTZ acts as an excellent antioxidant while, in lipid media, it behaves as a prooxidant due to the formation of the phenothiazinyl radical that is very stable and toxic to biological systems. In addition, in water, we suggest that PTZ is able to regenerate by means of the reaction between the radical cation formed initially by electron transfer to the attacking radical, PTZ˙+, and a superoxide radical anion, O2˙−. In this process, PTZ would hence be able to scavenge two radicals per cycle (the ˙OH or ˙OOH original attacking radical, and a superoxide radical anion, O2˙−) and to form molecular oxygen O2 in situ. Finally, we show that the dication PTZ++ that has been observed experimentally in water, can be easily formed if PTZ˙+ reacts with a second ˙OH radical.
Introduction
Oxidative stress is a widespread condition in the pathology of several neurodegenerative diseases, and it has been reported that reactive oxygen species (ROS) are directly implicated in many neurologic disorders and brain dysfunction.1 Indeed, the brain is believed to be particularly vulnerable to oxidative stress for several reasons: it contains high concentrations of polyunsaturated fatty acids that are susceptible to lipid peroxidation; it consumes relatively large amounts of oxygen for energy production; and it has lower antioxidant defenses compared to other organs. In order to overcome free radical-mediated consequences, neuroprotective antioxidants have been considered as a promising approach to slow down disease progression and to limit the extent of functional neuronal loss in chronic neurodegenerative disorders. Within this context, it has been suggested that the molecules that have shown beneficial effects in the treatment of neurodegenerative diseases owe their therapeutic action, at least in part, to their antioxidant properties.Phenothiazines are biologically active heterocyclic compounds that belong to a class of drugs used clinically to treat psychiatric disorders since the early 1950's. They are endowed with dopamine receptor antagonistic activities in the central nervous system (CNS).2 In addition, these drugs are used for clinical purposes as sedative,3,4 antihelmintics,5,6 anti-inflammatory, antimalarials, antibacterial,7,8 and anticonvulsants.9 Since phenothiazines have low ionization potentials, there have been suggestions that phenothiazine tranquilizers may be good electron donors and thus act as charge or electron transfer donors.10 In addition, phenothiazine and related compounds could exhibit an elevated free radical trapping action. Furthermore, phenothiazines are capable of crossing easily the blood–brain barrier, since they exhibit a strong affinity to lipid bilayers of the cell membranes in neurons and other lipid-rich tissues,11 and therefore, they could perform their antirradical action within the brain tissues. This is particularly important since 50% of dry brain weight is lipid, in contrast to 6–20% for other organs.
Phenothiazines have a tricyclic structure, with two phenyl rings bound by sulfur and nitrogen atoms.12 Their general chemical structure is given in Fig. 1. In the basic molecule, phenothiazine (PTZ), R2 = R10 = H.
The PTZ crystal structure shows that the molecule is folded about the N–S axis with the two planes containing the phenyl rings making a dihedral angle of 158.5°.13 Upon formation of its radical cation, the phenothiazine molecule opens, and the dihedral angle increases to 172°.14 Photoionization work15 suggests that the amine part of phenothiazine is pyramidal in the neutral ground state and planar in the radical cation ground state, thus favoring the π-orbital overlap.16 In recent studies, the photooxidation behavior of phenothiazine and its radical cations has been studied using time-resolved laser flash photolysis experiments.17 The radical cation formed by one-electron transfer exhibits two strong and characteristic optical absorptions λmax = 270 and 530 nm that can easily be detected and studied by time-resolved pulse radiolysis experiments. In addition, the photoelectron spectra of phenothiazine and its derivatives indicate that the first ionization potential is N-centered, and the second ionization potential, of slightly lower energy, is S-centered.18
The sensitivity of phenothiazines towards chemical oxidation has been investigated experimentally. It has been reported that the radical cations derived from them are pharmacologically active in the metabolism of phenothiazine-based drugs,19 and that they might be important intermediates in their biochemical action, especially in aqueous environments.20
The phenothiazine molecule has a rather small N–H bond dissociation energy (BDE) 79.3 ± 0.2,21 when compared, for example, with the BDE of the O–H bond in some of the most active radical trapping phenols, such as α-tocopherol, galvinol, and 2,4,6-trimethoxyphenol.22,23 A mechanism consisting of an electron transfer to an ˙OOR free radical has been suggested as the first step, with the formation of the radical cation of the amine.24 This is supported by the fact that the experimental value for the PTZ ionization potential is low, about 7 eV.25 The radical cation of PTZ is stable, and its EPR spectrum is well-known.26,27
Despite the great potential and practical interest of this class of molecules, not much is known about their reactivity towards free radicals, and data available in the literature are often contradictory. V. Hadjimitova et al.28 studied experimentally the antioxidant activity in vitro of six neuroleptic drugs (chlorpromazine, levomepromazine, promethazine, trifluoperazine and thioridazine) and two antidepressants (imipramine and amitriptyline) applying luminol-dependent chemiluminescence, and they demonstrated that phenothiazines are powerful scavengers of hydroxyl and superoxide radicals.28 In the case of PTZ, in addition to its antioxidant activity, a prooxidant activity has been reported in erythrocytes when the concentration of PTZ is large. G.-X. Li et al.29 have studied the hemolysis of human erythrocytes at different concentrations of PTZ and of a peroxyl radical supplier, 2,2′-azobis(2-amidinopropane hydrochloride), (AAPH). They found that, although PTZ can protect erythrocytes against AAPH-induced hemolysis, it can also act as a prooxidant when high concentrations are used. Under these conditions, PTZ is able to initiate hemolysis even in the absence of a radical initiator. The authors propose that high concentrations of PTZ may permeate into erythrocytes and be oxidized to ˙PTZ, which can induce additional radical propagation to oxidize polyunsaturated fatty acids in the membrane.
The two main functions of antioxidants are (1) to inhibit oxidation and (2) to stop the oxidation chain reaction. As a consequence, the primary antioxidant activity is related to the capacity of a certain molecule to sacrifice itself by becoming oxidized instead of an important biological target, and the most common role of an antioxidant is to scavenge free radicals. This occurs by a radical–molecule reaction. From a chemical point of view, the study involves the determination of its mechanism and kinetics, and the rate of this reaction is considered to be a measure of the antioxidant capacity of the molecule. The density functional theory (DFT) method has successfully been used to study the thermodynamic and kinetic aspects of radical–molecule reactions.
In order to quantify the antirradical reactivity of a certain molecule, it is usual to use the BDE and IP as thermodynamic parameters. However, when studying the reactivity of a certain molecule towards various different free radicals, these parameters are not sufficient to quantify the inhibition of the oxidative stress caused by each one of these free radicals. BDE reveal the lowest possible energy of the abstracted H atom from an R–H bond, to form an R-centered radical; although it can be very useful, the BDE parameter exhibits only the extent of the difficulty of a molecule to form a radical, but it does not exhibit the stabilization of the formed radical. With respect to the ionization potential, it is clear that a good electron donor should have low ionization energy and will tend to give electrons to a good electron acceptor. However, as discussed by Galano et al.,30 reaction kinetics offer a more accurate picture of reactivity than other possible indexes such as IE or BDE. In addition, overall rate coefficients take into account environmental aspects and the contributions of different mechanisms and sites of reactions.
No molecular study of the reaction mechanism and kinetics of PTZ with oxygen radical species in general has been published. In the present work, we report for the first time the results of a quantum chemistry and computational kinetics investigation aiming to assess the thermochemical and kinetic aspects of the initial step in the reaction of phenothiazine with ˙OH and ˙OOH free radicals and the superoxide anion O2˙−, which are relevant oxidative species under oxidative stress conditions. In order to mimic different biological environments, both water and lipid media were considered. Thermodynamic and kinetic data are provided, as well as a quantitative assessment of the contributions of the different mechanisms and channels of reaction, to the overall reactivity of PTZ towards the ˙OH and ˙OOH radicals. The hydroxyl radical (˙OH) was chosen because it is the most electrophilic and reactive one among all the oxygen-centered radicals, and it has a very short half-life of ∼109 s.31 The hydroperoxyl radical, ˙OOH, is the protonated form of the superoxide radical anion, O2˙−.32 Its protonation/deprotonation equilibrium exhibits a pKa of 4.8, indicating that only about 0.3% of any superoxide present in a typical cell is in the protonated form. However, O2˙− is not a very reactive species, so the chemistry of superoxide in living systems is probably dominated by ˙OOH radical reactions.33 The possible antioxidant vs. prooxidant role of PTZ will be discussed.
Computational methodology
All electronic calculations were performed with the Gaussian 09 package,34 using the QM-ORSA methodology.30 Geometry optimizations and frequency calculations have been carried out using the M06-2X functional in conjunction with the 6-311++G(d,p) basis set. The M06-2X functional has been recommended for kinetic calculations by its developers.35 Moreover, in a very recent work,36 Galano and Alvarez-Idaboy carried out a detailed benchmark study of 19 chemical reactions between different free radicals and closed-shell molecules, in order to test the performance of 18 exchange correlation functionals in conjunction with the 6-311++G(d,p) basis set, to calculate reaction rate constants in aqueous solution. Among them, the M06-2X functional was shown to yield excellent results.The unrestricted open-shell formalism was used for optimization of radical species. Frequency calculations were performed on optimized geometries to establish the nature of the stationary point on the potential energy surface: local minima have only real frequencies, while transition states are identified by the presence of a single imaginary frequency that corresponds to the expected motion along the reaction coordinate. Relative energies are calculated with respect to the sum of the separated reactants. Zero-point energies (ZPE) and thermal corrections to the energy (TCE) at 298.15 K, which correspond to a 1 M standard state, are included in the determination of energy barriers.
In this work, solvent effects are introduced with the SMD continuum model37 using water and pentylethanoate as solvents, in order to mimic aqueous and lipid biological environments. SMD is considered to be a universal solvation model, due to its applicability to any charged or uncharged solute in any solvent or liquid medium for which a few key descriptors are known.37 In this work, for anionic species, we have used the following solvation energies derived from experiment: ΔGsolv(OH−) = −105 kcal mol−1 and ΔGsolv(OOH−) = −97.7 kcal mol−1, on the basis of the recommendation of Pliego and Riveros.38
Solvent cage effects have been included according to the corrections proposed by Okuno,39 taking into account the free volume theory.40 The expression used to correct the Gibbs free energy is:
| ΔGFVsol ≅ ΔG0sol − RT{ln[n10(2n−2)] − (n − 1)} | (1) |
Rate constants have been computed using conventional Transition State Theory (TST),41 according to:
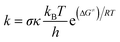 | (2) |
For mechanisms involving a single electron transfer (SET), the Marcus theory was used.44 It relies on the transition state formalism, defining the SET activation barrier (ΔG≠SET) in terms of two thermodynamic parameters, the free energy of reaction (ΔGSET) and the nuclear reorganization energy (λ):
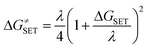 | (3) |
The reorganization energy (λ) is the energy associated with the nuclear rearrangement involved in the formation of products in a SET reaction, which implies not only the nuclei of the reacting species but also those of the surrounding solvent. The reorganization energy (λ) is calculated as:
| λ = ΔESET − ΔGSET | (4) |
When the reaction rate constants are within the diffusion-limited regime, they cannot be directly obtained from TST calculations. In this case, any encounter between reactants is limited by the rate at which they can diffuse within the solvent. Therefore, any rate constant larger than the diffusion rate lacks physical meaning. Moreover, any calculated rate constant intended to reproduce the actual behavior of a system under experimental (in vitro or in vivo) conditions must be directly comparable with the observable one.30 We will refer to the latter as the apparent rate constant (kapp). In the present work, the Collins–Kimball theory46 is used to correct the rate constant, and kapp is calculated as:
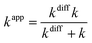 | (5) |
| kdiff = 4πRABDABNA | (6) |
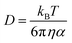 | (7) |
The total rate coefficient for each mechanism is calculated as the sum of the individual rate constants for all channels of this mechanism. The overall rate coefficient (koverall), in each solvent, is calculated as the sum of the total rate constants for all the considered mechanisms.
Results and discussion
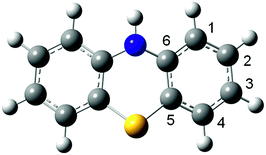
The PTZ structure has been determined using quantum chemistry calculations. The optimized structure is shown in Fig. 2, where we have also indicated the atomic numbering scheme. Hydrogen, carbon, nitrogen and sulphur atoms are in white, grey, blue and yellow colours, respectively.In the PTZ optimized structure, the two benzene rings form a dihedral angle along the line between S and NH.
Fig. 3 shows the shape of the phenothiazine molecule frontier orbitals. The red and green colors represent the positive and negative phases, respectively.
It can be observed that the HOMO is a π-bonding orbital strongly localized on the S and N atoms, while the LUMO is mainly an antibonding π*-orbital in character. Thus, it is expected that the reactivity of PTZ towards electrophilic free radicals such as ˙OH and ˙OOH, will involve most probably the S and N donating atoms.
PTZ exists in a neutral form in aqueous solution at physiological pH. Since blood can be modelled as an aqueous solution at pH = 7.4, in this work the neutral form will be used to study the reactivity of PTZ towards ˙OH and ˙OOH free radicals both in water and lipid media.
We have considered three possible reaction mechanisms:
(i) One electron transfer from the neutral molecule to the free radical (single electron transfer, SET):
| PTZ + ˙OH → PTZ˙+ + OH− |
| PTZ + ˙OOH → PTZ˙+ + OOH− |
(ii) Hydrogen atom transfer from the neutral molecule to the free radical (hydrogen atom transfer, HAT):
| PTZ + ˙OH → PTZ˙ + H2O |
| PTZ + ˙OOH → PTZ˙ + H2O2 |
and (iii) Radical addition to the neutral molecule (radical adduct formation, RAF):
| PTZ + ˙OH → [PTZ–OH]˙ |
| PTZ + ˙OOH → [PTZ–OOH]˙ |
These channels could occur in parallel, but at different rates. One of the objectives of the present paper is to determine which mechanism has the fastest rate constant in the reactions of PTZ with hydroxyl (˙OH) and hydroperoxyl (˙OOH) free radicals.
All of the above reactions may be responsible for some of the beneficial and/or adverse effects of administered phenothiazine drug. For example, in the HAT mechanism the phenothiazinyl radical is formed. This radical is known to be very stable and toxic to biological systems.
For the reaction of PTZ with ˙OH and ˙OOH radicals in aqueous environment, we have studied the HAT, RAF and SET mechanisms described above. In lipid media, only the HAT and RAF mechanisms are considered; the SET mechanism is not expected to occur in non-polar environments because it does not promote the necessary solvation of the intermediate ionic species yielded by this mechanism.
Since the most effective inhibition of oxidative stress occurs if the reaction chain is interrupted at the rate determining step, then it is necessary to calculate the reaction barriers and the absolute rate constants and branching ratios of all the individual feasible reaction channels, and the overall rate constants for each radical in the first step of the PTZ oxidation. In what follows, we have characterized the stationary points along the reaction coordinate for all the viable reaction channels. At this point, we wish to emphasize the need to reoptimize stationary structures in the solvent, rather than performing single-point calculations at the gas phase geometries. This is especially important in polar solvents, since they favor charge separation and may lead to significant geometrical changes.
I. Thermodynamic feasibility
For each mechanism, the thermochemical feasibility of all the different channels was investigated first, since it determines the viability of the referred chemical processes. For the HAT mechanism, we have only considered the hydrogen atom transfer from the N–H site to the free radical, with the formation of the corresponding aminoxyl radical and a water molecule. For the RAF mechanism, there are six possible reaction pathways that correspond to the oxygen atom of the free radical binding to any one of the carbon atoms in the molecule.Relative reaction Gibbs free energies (including TCE at 298.15 K) for the HAT, SET and RAF channels of the ˙OH and ˙OOH radicals have been calculated with respect to the sum of the separated reactants, in water and pentylethanoate, and they are reported in Table 1.
| Reaction channel | Water | Pentylethanoate |
|---|---|---|
| ΔG(˙OH) | ||
| SET | −32.29 | — |
| HAT | −42.47 | −37.34 |
| RAF 1 | −12.34 | −9.75 |
| RAF 2 | −10.79 | −7.79 |
| RAF 3 | −12.44 | −9.59 |
| RAF 4 | −10.40 | −7.51 |
| RAF 5 | −15.19 | −12.53 |
| RAF 6 | −11.33 | −8.56 |
| ΔG(˙OOH) | ||
|---|---|---|
| SET | −17.29 | — |
| HAT | −10.26 | −4.86 |
| RAF 1 | 12.77 | 16.51 |
| RAF 2 | 13.92 | 18.69 |
| RAF 3 | 12.71 | 16.86 |
| RAF 4 | 14.90 | 18.98 |
| RAF 5 | 12.52 | 15.96 |
| RAF 6 | 16.16 | 19.89 |
For the ˙OH radical, all reactions are exergonic, and the HAT reaction channel is clearly thermodynamically favored in both media. It can be observed that all paths are considerably more exergonic in water than in lipid media, due to the polarity of the solvent. Addition of ˙OH to position 5 yields the most stable RAF adduct.
For the ˙OOH radical, all the RAF reaction pathways are endergonic by more than 12.5 kcal mol−1 and they will not be considered further. The HAT reaction is exergonic in both media, and the SET reaction is exergonic in water. Although the reaction free energies are, in all cases, considerably smaller than with ˙OH, these mechanisms may still contribute significantly to the radical scavenging activity of PTZ.
For the kinetic study, we have not included those reaction paths that were found to be endergonic or close to zero, because, even if they took place at significant rates, they would be reversible, and the formed products would not be observed. However, they might still represent significant channels if their products, in turn, react rapidly. This would be particularly important if these further stages were sufficiently exergonic to provide a driving force, and if their reaction barriers were low.30
In conclusion, for the reaction of PTZ with ˙OH radicals in water, we have considered all three mechanisms, while for ˙OOH, only the HAT and SET mechanisms have been studied. In pentylethanoate, HAT and RAF are possible with ˙OH, while only HAT is exergonic for the ˙OOH radical. This is in line with the smaller reactivity of the ˙OOH radical compared with ˙OH.
II. Reactivity of PTZ towards ˙OH and ˙OOH radicals in water
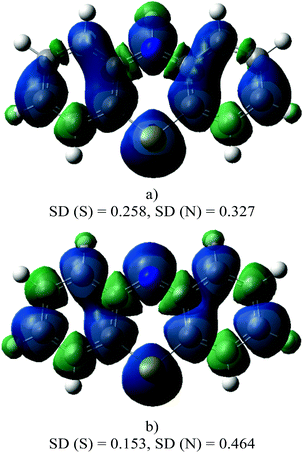
The spin density distribution on the radical cation and on the phenothiazinyl radical are shown in Fig. 5. In the radical cation, the electron is mainly located on the N atom (spin density on N = 0.327). It can be seen that, after the loss of the proton, the N atom spin density increases, while it decreases on the S atom.
The phenothiazinyl radical is stabilized through delocalization of the unpaired electron. The single electron of the N-centered radical is delocalized over the whole PTZ molecule. As mentioned before, in PTZ, the two benzene rings form a dihedral angle along the line between S and N–H, but in the PTZ˙ radical they are located on the same plane. The coplanarity of these two benzene rings allows the nitrogen p orbital to participate in the π-bond formed by the two benzene rings. The large conjugative system stabilizes the PTZ˙.
Gibbs free energies of activation (ΔG≠SET), free reaction energies (ΔGSET), reorganization energies (λ), diffusion rate constants (kdiffSET), thermal rate constants (kSET) and apparent rate constants (kappSET) for the SET reactions of PTZ with the studied radicals, in aqueous solution at physiological pH, are reported in Table 2. ΔG≠SET has been evaluated using the Marcus theory. Apparent rate constants (kappSET) were calculated using the Collins–Kimball theory. The diffusion rate constant kD has been calculated according to eqn (6), and it is also included in this table for comparison.
| SET reaction | ΔG≠SET | ΔGSET | λ | kdiffSET | kSET | kappSET |
|---|---|---|---|---|---|---|
| PTZ + ˙OH → PTZ˙+ + OH− | 0.00 | −18.43 | 18.64 | 8.31 × 109 | 1.52 × 1014 | 8.31 × 109 |
| PTZ + ˙OOH → PTZ˙+ + OOH− | 10.01 | 4.99 | 29.20 | 8.14 × 109 | 6.98 × 106 | 6.97 × 106 |
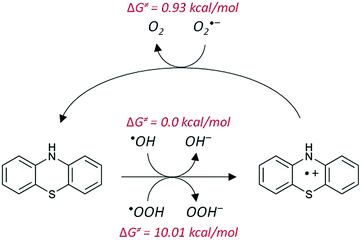
| PTZ˙+ + O2˙− → PTZ + O2 | 0.93 | −26.68 | 18.40 | 7.84 × 109 | 3.16 × 1013 | 7.84 × 109 |
The calculated activation energy for the ˙OH radicals is almost 0.0 kcal mol−1, as the reaction Gibbs free energy is almost equal to the negative value of the reorganization energy (λ). Thus, this reaction is located on the Marcus parabola vortex, and the activation free energy tends to 0, according to eqn (3). Consequently, in this case, the SET process for the ˙OH radical is diffusion-controlled. The subsequent proton transfer could be very fast in a polar medium, and its corresponding rate constant could also be diffusion-controlled.
For the ˙OOH radical, the calculated activation barrier is 10.01 kcal mol−1, much higher than in the case of ˙OH radicals. However, the calculated SET rate constant is also quite large.
Thus, PTZ is clearly a very efficient scavenger of both ˙OH and ˙OOH radicals through the SET mechanism in aqueous solution at physiological pH. Moreover, we will show that PTZ has the ability to regenerate and to scavenge more than one free radical. This point will be addressed in the next section.
In our case, once the PTZ molecule transfers an electron to the ˙OH or ˙OOH radical, the formed PTZ radical cation could react with a different radical species. As O2˙− is present in relatively large concentrations in biological media, we propose that PTZ˙+ accepts an electron from O2˙−; thus PTZ is regenerated and molecular O2 is formed. At this point, it is important to note that, since the superoxide radical anion does not cross membranes easily,51 its damaging effects would be restricted to the cells that generate it. This means that PTZ would be able to neutralize undesirable O2˙− and form beneficial O2 that is required for cellular respiration in situ. In contrast, the neutral protonated form of superoxide (˙OOH) could traverse biological membranes, although its low intracellular concentration provides a low driving force for diffusion into adjacent cellular compartments.51
Gibbs free energies of activation (ΔG≠SET), free reaction energies (ΔGSET), reorganization energies (λ), diffusion rate constants (kdiffSET), thermal rate constants (kSET) and apparent rate coefficients (kappSET) for the SET reactions in the regeneration mechanism of PTZ, in aqueous solution at physiological pH, are reported in Table 2.
The reaction barrier for the recombination of the reacting PTZ˙+ + O2˙− radicals is close to zero (0.93 kcal mol−1). This reaction corresponds to the inverted region of the Markus theory that is characterized by having the reaction free energy lower than the negative value of the reorganization energy (ΔG < −λ).52 However, it is close to the vertex of the Marcus parabola and therefore its barrier remains low, and the corresponding reaction rate will be very fast. Indeed, our calculations show that this reaction is limited by diffusion.
Hence, it is reasonable to assume that the proposed mechanism competes with the proton transfer, since both occur at diffusion-controlled rates. Furthermore, the recombination of two radicals (in this case, PTZ˙+ and O2˙−) is expected to be favored over the breaking of the N–H bond, which implies the motion of a proton instead of an electron. Thus, the regeneration process seems to be a very probable pathway for PTZ˙+ and, in the end, PTZ would then be able to scavenge two free radicals per cycle: the original attacking radical (˙OH or ˙OOH) and O2˙−.
The proposed mechanisms for PTZ regeneration in water is presented schematically in Fig. 6. We have indicated, in red, the values of the activation barriers in terms of Gibbs free energies.
In turn, we have investigated the reaction of the dication with O2˙−, which regenerates PTZ˙+. The results are presented in Table 2, for ˙OH and ˙OOH radicals.
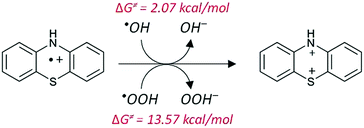
The results in Table 3 show that the reaction only happens with ˙OH radicals; while ˙OOH is not capable of removing a second electron to form the dication. The regeneration of PTZ˙+ by means of the PTZ++ + O2˙− reaction presents a very large and negative ΔG, and the corresponding rate constant is diffusion-controlled.
| SET reaction | ΔG≠SET | ΔGSET | λ | kdiffSET | kSET | kappSET |
|---|---|---|---|---|---|---|
| PTZ˙+ + ˙OH → PTZ++ + OH− | 5.14 | 4.51 | 9.37 | 8.35 × 109 | 2.59 × 1010 | 6.31 × 109 |
| PTZ˙+ + ˙OOH → PTZ++ + OOH− | 28.73 | 27.93 | 19.93 | 8.17 × 109 | 1.32 × 10−7 | 1.32 × 10−7 |
| PTZ++ + O2˙− → PTZ˙+ + O2 | 15.20 | −49.61 | 17.24 | 7.98 × 109 | 2.59 × 1010 | 6.10 × 109 |
The proposed mechanism for the formation of the dication is presented schematically in Fig. 7. We have indicated, in red, the values of the activation barriers in terms of Gibbs free energies.
The PTZ˙+ + ˙OH reaction is also expected to lead to a variety of addition adducts by means of radical recombination reactions (RAF).
The same should be true for PTZ˙+ + ˙OOH as well as for most any available radical. However, as an electron transfer can occur at distances between the reactants that are considerably larger than in addition reactions,53 it seems reasonable to expect that this mechanism will prevail.
The transition states for the PTZ + ˙OH and PTZ + ˙OOH reactions were easily located and characterized in the gas phase. However, it was not possible to locate them in water using full optimizations. A careful mapping of the potential energy surfaces indicates that, in water, H-abstraction from the N–H group of PTZ is a barrierless process, for both ˙OH and ˙OOH radicals, and it occurs without the formation of a pre-reactive complex. Using partial optimization with constrained N⋯H⋯OH bonds, we were able to obtain a structure that presents an imaginary frequency. The subsequent unfreezing of the two distances involved, followed by optimization to a saddle point, produces an increase of the H⋯OH distance, and a corresponding decrease of the imaginary frequency and of the gradient, leading to the separated reactants. A relaxed scan, obtained by decreasing the H⋯OH distance, produces an equivalent result: in this case, the energy decreases until the H atom is completely transferred. This means that the reaction is strictly diffusion-controlled, i.e. every encounter results in a reaction.
The diffusion rate constants for the ˙OH and ˙OOH radicals are calculated from eqn (6). The calculated rate for the diffusion of the ˙OH radical in water when reacting with PTZ through a HAT mechanism, is 2.82 × 109 M−1 s−1, and for ˙OOH is 2.70 × 109 M−1 s−1.
All the stationary points have been characterized on the potential energy surface of the reactions considered. The optimized geometries of the transition structures in the RAF pathways are presented in Fig. 8, along with the corresponding C⋯O non-bonding distances (in Å) and activation Gibbs free energies.
 | ||
| Fig. 8 Optimized transition structures in the RAF reaction channels between PTZ and ˙OH radicals, in water. | ||
All additions occur in a similar way and destroy the aromaticity of the ring. The ˙OH radical oxygen atom approaches a carbon atom of the benzene ring. The transition vector in the transition states (TS) structures corresponds to the vertical movement of the OH group in the direction of the carbon site. The H atom attached to the carbon atom folds back slightly to accommodate the incoming ˙OH radical. In these TS, the distance between the ˙OH radical and the C atom ranges from 2.092 to 2.315 Å. Only six adducts are formed, as the transitions states on both sides of the molecule yield the same final radical adduct.
Relative enthalpies of activation (ΔH≠RAF) including ZPE, and Gibbs free energies of activation (ΔG≠RAF) including TCE at 298.15 K, are calculated with respect to the sum of the separated reactants at 0 K, in aqueous solution at physiological pH, and they are reported in Table 4. The smallest Gibbs free energy of activation corresponds to the RAF-5 channel (1.63 kcal mol−1), followed by RAF-6 and RAF-3 (2.53 kcal mol−1 and 3.56 kcal mol−1, respectively). Thus, in water, the RAF-5 site is preferentially attacked by ˙OH radicals through a RAF mechanism. Analyzing the magnitude of d(O–C) in the transition states and the Gibbs free energy of reaction for the different RAF channels, it can be noticed that the earlier the transition state (more reactant-like) the lower the ΔG value, which is in line with the Hammond postulate.54
| RAF path | ΔH≠RAF | ΔG≠RAF | kRAF | kappRAF |
|---|---|---|---|---|
| Solvent = water | ||||
| 1 | −2.83 | 3.79 | 5.07 × 1011 | 1.56 × 109 |
| 2 | −0.48 | 5.85 | 1.57 × 1010 | 1.42 × 109 |
| 3 | −2.63 | 3.56 | 7.47 × 1011 | 1.56 × 109 |
| 4 | 0.14 | 6.85 | 2.90 × 109 | 1.02 × 109 |
| 5 | −5.16 | 1.63 | 1.94 × 1013 | 1.57 × 109 |
| 6 | −4.36 | 2.53 | 4.25 × 1012 | 1.57 × 109 |
| ktotalRAF | 8.70 × 109 | |||
Corresponding thermal rate constants (kRAF) and apparent rate constants (kappRAF) for the RAF channels are also reported in Table 4. The calculated rate for the diffusion of the ˙OH radical in water when reacting with PTZ through a RAF mechanism was calculated using eqn (6), and its value is 1.57 × 109 M−1 s−1. The distance required for the bimolecular reaction to take place is taken from the transition state, and it is equal to the distance between the two atoms that are involved in the forming bond. We have not calculated the tunneling correction, because the enthalpies of activation are very low, and they are negative in almost all cases. In addition, it is well-known that tunneling corrections are not important for reactions that do not involve light particles. The total rate constant for the RAF mechanism (ktotalRAF), calculated as the sum of all the independent RAF channels is also reported in Table 4.
The apparent rate coefficients for all the RAF channels of ˙OH radicals are also close to or diffusion-controlled, and therefore, no selectivity is observed, even though the Gibbs free energies of activation are different. Our conclusion is that ˙OH-addition to PTZ also constitutes an important mechanism that yields six possible ring-hydroxylated adducts.
In a water environment, phenothiazine reacts with ˙OH radicals at diffusion-controlled rates, independently of the reaction mechanism, and so, the overall rate constant must be mandatorily diffusion-controlled. The calculated overall rate constant for the ˙OH radical in water is 1.98 × 1010 M−1 s−1. However, as an electron transfer can occur at distances between the reactants that are considerably larger than in addition reactions,53 it seems reasonable to expect that the SET mechanism will prevail.
The ˙OOH radicals only react with PTZ mainly through the HAT mechanism, also at diffusion-controlled rate constant. As the product of the HAT reaction is the toxic phenothiazinyl radical, we suggest that PTZ could act as a prooxidant, as observed by G.-X. Li et al.29 The calculated overall rate constant for the ˙OOH radical in water is 2.70 × 109 M−1 s−1.
These findings mean that, kinetically, in aqueous solution at physiological pH, PTZ exhibits an extremely high reactivity towards both ˙OH and ˙OOH radicals. These results can be compared, for example, with calculated and experimental rate constants obtained for trolox (Table 5), which is frequently used as an antioxidant reference.
| Reaction | koverall | kexperimental |
|---|---|---|
| PTZ + ˙OH | 1.98 × 1010 | |
| Trolox + ˙OH | 2.78 × 1010 | 8.10 × 1010 |
| PTZ + ˙OOH | 2.70 × 109 | |
| Trolox + ˙OOH | 8.90 × 104 |
PTZ and trolox react with ˙OH at very similar reaction rates, while the reaction with ˙OOH is thirty thousand times faster for PTZ than for trolox. Based on kinetic considerations, the PTZ + ˙OOH reaction rate constant in water is predicted to be unusually high, much higher than for example, that of allicin (7.4 × 103 M−1 s−1),56 dopamine (2.2 × 105 M−1 s−1),57 canolol (2.50 × 106 M−1 s−1),58 glutathione (2.7 × 107 M−1 s−1),59 sesamol (2.4 × 108 M−1 s−1),60 propyl gallate (4.56 × 108 M−1 s−1),61 and fraxetin (4.12 × 108 M−1 s−1).62
As the ˙OOH damage to fatty acids is known to occur at much smaller rate constants,55 it is evident that PTZ protects efficiently against oxidative stress caused by ˙OOH radicals and also probably other peroxyl radicals. This is especially important because, contrary to ˙OH radicals that react very fast with any biological molecule, ˙OOH radicals are less reactive and have a much larger half-life. Therefore, their impact on oxidative stress is very high.
III. Reactivity of PTZ towards ˙OH and ˙OOH radicals in lipid media
The results presented in Table 1 indicate that, in the non-polar pentylethanoate solvent, the HAT mechanism is exergonic for both ˙OH and ˙OOH radicals. The RAF reaction channels of the ˙OH radical are also exergonic, while for the ˙OOH radicals, they all are considerably endergonic, as was the case in water. This means that, independently of the environment's polarity, the RAF mechanism for the ˙OOH radicals is not expected to contribute to the free radical scavenging activity of PTZ. Consequently, in what follows, we have investigated the HAT mechanisms for both ˙OH and ˙OOH radicals, and the RAF reaction channels only for ˙OH radicals. | ||
| Fig. 9 Transition structures in the HAT reaction of PTZ with ˙OH and ˙OOH radicals, in pentylethanoate. | ||
Thermal rate constants were calculated for these reactions. Relative enthalpies (ΔH≠) including ZPE, Gibbs free energies of activation (ΔG≠) including TCE at 298.15 K, and thermal rate constants (k), for the HAT reactions involving the studied radicals, in pentylethanoate, are reported in Table 7. The calculated diffusion rate for the ˙OH radical in pentylethanoate through a HAT mechanism is 2.15 × 109 M−1 s−1. In lipid media, the HAT reaction of PTZ with ˙OH radicals is close to the diffusion limit, while with ˙OOH radicals it is negligibly slow (15.56 M−1 s−1).
| Radical | ΔH≠HAT | ΔG≠HAT | kdiffHAT | kHAT | kappHAT |
|---|---|---|---|---|---|
| ˙OH | −1.40 | 6.88 | 2.11 × 109 | 1.37 × 109 | 8.32 × 108 |
| ˙OOH | 7.72 | 18.13 | 2.02 × 109 | 7.78 | 7.78 |
| RAF path | ΔH≠RAF | ΔG≠RAF | kRAF |
|---|---|---|---|
| Solvent = pentylethanoate | |||
| 1 | −1.40 | 7.53 | 9.19 × 108 |
| 2 | 1.73 | 10.94 | 2.91 × 106 |
| 3 | −0.21 | 8.66 | 1.36 × 108 |
| 4 | 1.74 | 10.80 | 3.68 × 106 |
| 5 | −0.83 | 8.83 | 1.02 × 108 |
| 6 | 0.21 | 9.36 | 4.19 × 107 |
| ktotalRAF | 1.20 × 109 | ||
In the HAT mechanism, PTZ behaves as a prooxidant due to the formation of the phenothiazinyl radical that is very stable and toxic to biological systems.
The lowest activation barrier corresponds to the RAF-1 channel, in contrast with the one found in aqueous solution (RAF-5). This indicates that the relative site reactivity, via RAF, is influenced by the environment.
In pentylethanoate solvent, the calculated values for the ˙OH RAF channels rate coefficients are quite large, between 106 and 108 M−1 s−1. For comparison, the calculated rate constant for the diffusion of the ˙OH radical in lipid media for the RAF mechanism is 1.62 × 109 M−1 s−1. The calculated total rate constant for the RAF mechanism (ktotalRAF) is 1.20 × 109 M−1 s−1.
Thus, in lipid media, PTZ is an excellent ˙OH radical scavenger that reacts through HAT and RAF mechanisms at a rate constant that is close to the diffusion of the radical, with an overall contribution from all the RAF channels that amounts to about the same as for HAT. Contrary to the PTZ + ˙OH reactions in water that are diffusion-controlled, in lipid media, these reactions are activation-controlled.
As mentioned in the case of the HAT reaction in water, in lipid media PTZ could also act as a prooxidant when reacting with ˙OH radicals, due to the formation of the toxic and relatively stable phenothiazinyl radical.
The ˙OOH radical only reacts through the HAT mechanism, but at a very low rate constant, and it is clear that PTZ does not efficiently act as an ˙OOH radical scavenger in lipid media.
Conclusions
In this work, we have carried out a mechanistic quantum chemistry study of the reactivity of the phenothiazine molecule towards ˙OH and ˙OOH radicals, in aqueous and lipid simulated biological environments. All thermodynamically feasible reaction pathways have been investigated.In water, we find that the overall rate constants for both ˙OH and ˙OOH radicals are diffusion-controlled, independently of the reaction mechanism. However, since the SET mechanism involves the motion of an electron instead of a proton or a radical, it can be argued that this mechanism would be the predominant one.
In addition, we have proposed a regeneration route by means of the reaction of a superoxide anion radical with the radical cation, PTZ˙+, formed in the SET reaction. According to this mechanism, PTZ would be able to inactivate two radicals (an ˙OH/˙OOH and an O2˙−) per cycle. Thus, PTZ could be considered to be an excellent antioxidant towards ˙OH, ˙OOH and O2˙− radicals, in aqueous solution at physiological pH, even if it is present in a relatively low concentration. Its radical scavenging capacity appears to be even superior to that of most known antioxidants.
It must be emphasized that the possibility to regenerate is essential and should be considered when evaluating the radical scavenging capacity of a certain antioxidant. If the predominant mechanism is addition of a free radical to form stable radical adducts (RAF), structural changes occur, and it would be difficult to regenerate the original molecule. In contrast, when the predominant mechanism is an electron transfer (SET), structural changes are minimal, and the possibility of regeneration through reactions with other free radicals could be very important.
Finally, in water, if PTZ˙+ reacts with a second ˙OH radical, we have shown that it easily forms a dication, PTZ++. This species has been observed experimentally.
In lipid media, only the HAT and RAF mechanisms occur. Thus, the regeneration mechanism is ruled out. The overall rate constant for the ˙OH radicals is close to the diffusion limit, but it is very small for ˙OOH radicals. In the PTZ + ˙OH reaction under these conditions, the HAT mechanism predominates over the RAF channels, and its overall rate constant is twice as large as the sum of the rate constants of all the RAF channels. The phenothiazinyl radical formed in the HAT mechanism is toxic to biological systems, and it has been reported that it oxidizes polyunsaturated fatty acids in erythrocytes membranes. Thus, PTZ would act as a prooxidant agent in lipid media.
The antioxidant vs. prooxidant activity of PTZ depends on the reacting radical as well as on the biological media.
Acknowledgements
We gratefully acknowledge the Laboratorio de Visualización y Cómputo Paralelo at Universidad Autónoma Metropolitana-Iztapalapa for computer time.Notes and references
- (a) H. A. Kontos and E. George, Circ. Res., 1985, 57, 508D16 Search PubMed; (b) B. K. Siesjo, C. D. Agardh and F. Bengtsson, Cerebrovascular and brain metabolism reviews, 1989, 1, 165D211 Search PubMed; (c) P. H. Chan, J. Brain Pathol., 1994, 4, 59D65 Search PubMed.
- W. W. Shen, Compr. Psychiatry, 1999, 40, 407 CrossRef CAS.
- R. Hazard, E. Corteggiani and A. Cornec, C. R. Soc. Biol., 1950, 143, 906 Search PubMed.
- Y. Kase and T. Yuizonto, Chem. Pharm. Bull., 1959, 7, 378 CrossRef CAS.
- L. E. Swanson, D. A. Porter and J. W. Connelly, J. Am. Vet. Med. Assoc., 1940, 96, 704 CAS.
- H. A. Oelbers and D. Bovet, Arzneim. Forsch., 1951, 5II, 139 Search PubMed.
- V. G. Longo and D. Bovet, Farm. Sci. e Techn., 1950, 4, 515 Search PubMed.
- J. Mahaux and K. K. Kowalewski, Arch. Int. Pharmacodyn. Ther., 1949, 80, 464 CAS.
- A. Balestrieri, Arch. Intern. Pharmacodynamie, 1955, 100, 361 CAS.
- J. E. Bloor, J. Med. Chem., 1970, 13, 922 CrossRef CAS.
- A. Seelig, R. Gottschlich and R. M. Devant, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 68 CrossRef CAS.
- H. Vakifahmetoglu, M. Olsson and B. Zhivotovsky, Cell Death Differ., 2008, 15, 1153 CrossRef CAS PubMed.
- (a) J. J. H. McDowell, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 5 CrossRef; (b) J. D. Bell, J. F. Blount, O. V. Briscoe and H. C. Freeman, Chem. Commun., 1968, 1656 RSC.
- A. Sighanbandhu, P. D. Robindon, J. H. Fang and W. E. Geiger, Inorg. Chem., 1975, 14, 318 CrossRef.
- N. L. Domelsmith, L. L. Munchausen and K. N. Houk, J. Am. Chem. Soc., 1977, 99, 6506 CrossRef.
- D. Clarke, B. C. Gilbert, P. Hanson and M. C. Kirk, J. Chem. Soc., Perkin Trans. 1, 1978, 2, 1103 RSC.
- (a) Q. X. Guo, Z. X. Liang, B. Liu, S. D. Yao and Y. C. Liu, J. Photochem. Photobiol., A, 1996, 93, 27 CrossRef CAS; (b) C. Garcia, G. A. Smith, W. M. McGimpsey, I. E. Kochevar and R. W. Redmond, J. Am. Chem. Soc., 1995, 117, 10871 CrossRef CAS.
- N. L. Domelsmith, L. L. Munchausen and K. N. Houk, J. Am. Chem. Soc., 1977, 99, 6506 CrossRef.
- (a) C. M. Gooley, H. Keyzer and F. Setchell, Nature, 1969, 223, 81 CrossRef; (b) G. Testylier, D. Daveloose, F. Leterrier, O. Buchman and M. Shimoni, Photochem. Photobiol., 1984, 39, 273 CrossRef CAS PubMed; (c) S. Ohnishi and H. M. McConnell, J. Am. Chem. Soc., 1965, 87, 2293 CrossRef CAS.
- (a) P. P. Kelder, N. J. de Mol and L. H. M. Janssen, Biochem. Pharmacol., 1991, 42, 1551 CrossRef CAS; (b) A. Vasquez, J. Tudela, R. Varon and F. A. Garcia-Canovas, Biochem. Pharmacol., 1992, 44, 889 CrossRef; (c) Y. Moroi, A. M. Braun and M. Gratzel, J. Am. Chem. Soc., 1979, 101, 567 CrossRef CAS; (d) M. C. Hovey, J. Am. Chem. Soc., 1982, 104, 4196 CrossRef CAS; (e) N. Younthan, W. E. Jones Jr and T. J. Meyer, J. Phys. Chem., 1991, 95, 488 CrossRef; (f) N. J. Turro, I. V. Khudyakov and H. van Willigen, J. Am. Chem. Soc., 1995, 117, 12273 CrossRef CAS; (g) K. Nakagawa, A. Katsuki, S. Tero-Kubota, N. Tsuchihashi and T. Fujita, J. Am. Chem. Soc., 1996, 118, 5778 CrossRef CAS.
- M. Lucarini, P. Pedrielli, G. F. Pedulli, L. Valgimigli, D. Gigmes and P. Tordo, J. Am. Chem. Soc., 1999, 121, 1999 CrossRef.
- M. Lucarini, G. F. Pedulli and M. Cipollone, J. Org. Chem., 1994, 59, 5063 CrossRef CAS.
- M. Lucarini, P. Pedrielli, G. F. Pedulli, S. Cabiddu and C. Fattuoni, J. Org. Chem., 1996, 61, 9259 CrossRef CAS.
- I. A. Kabanova, A. M. Dubinskaya, N. I. Yurchenko and V. I. Goldenberg, Kinet. Katal., 1987, 28, 816 CAS.
- L. Domelsmith, L. Munchausen and K. Houk, J. Am. Chem. Soc., 1977, 99, 6506 CrossRef CAS.
- M. F. Chiu, B. C. Gilbert and P. Hanson, J. Chem. Soc. B, 1970, 1700 RSC.
- F. L. Rupérez, J. C. Conesa and J. Soria, Spectrochim. Acta, Part A, 1984, 40, 1021 CrossRef.
- V. Hadjimitova, T. Traykov, M. Mileva and S. Ribarov, Psychotropic Drugs and Chemiluminescence in Model Systems, 2002 Search PubMed.
- G.-X. Li, Y.-Z. Tang and Z.-Q. Liu, J. Biochem. Mol. Toxicol., 2009, 23, 81 CrossRef PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430 CrossRef CAS PubMed.
- I. G. Draganic and Z. D. Draganic, The Radiation Chemistry of Water, Academic Press, New York, 1971 Search PubMed.
- A. D. N. J. de Grey, DNA Cell Biol., 2002, 21, 251 CrossRef CAS PubMed.
- E. J. Land and M. Ebert, Trans. Faraday Soc., 1967, 63, 1181 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- J. R. Pliego Jr and J. M. Riveros, Chem. Phys. Lett., 2000, 332, 597 CrossRef.
- Y. Okuno, Chem.–Eur. J., 1997, 3, 212 CrossRef CAS PubMed.
- S. W. Benson, The Foundations of Chemical Kinetics, Krieger, FL, 1982 Search PubMed.
- (a) H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS PubMed; (b) M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875 RSC; (c) D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2264 CrossRef.
- D. G. Truhlar and A. Kuppermann, J. Am. Chem. Soc., 1971, 1840 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- (a) R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155 CrossRef CAS; (b) R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS; (c) R. A. Marcus, Pure Appl. Chem., 1997, 69, 13 CrossRef CAS.
- (a) S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677 CrossRef CAS; (b) S. F. Nelsen, M. N. Weaver, Y. Luo, J. R. Pladziewicz, L. K. Ausman, T. L. Jentzsch and J. J. O'Konek, J. Phys. Chem. A, 2006, 110, 11665 CrossRef CAS PubMed.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425 CrossRef CAS.
- M. Smoluchowski, Z. Phys. Chem., 1917, 92, 129 Search PubMed.
- D. G. Truhlar, J. Chem. Ed., 1985, 62, 104 CrossRef CAS.
- (a) A. Einstein, Ann. Phys., 1905, 17, 549 CrossRef CAS; (b) G. G. Stokes, Mathematical and Physical Papers, Cambridge University Press, Cambridge, 1903, vol. 3, esp. sect. IV, p. 55 Search PubMed.
- (a) A. Galano and A. Pérez-González, Theor. Chem. Acc., 2012, 131, 1265 CrossRef PubMed; (b) M. E. Medina, A. Galano and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2014, 16, 1197 RSC; (c) M. E. Medina, C. Iuga and J. R. Alvarez-Idaboy, RSC Adv., 2014, 4, 52920 RSC.
- M. Ganesana, J. S. Erlichman and S. Andreescu, Free Radical Biol. Med., 2012, 53(12), 2240 CrossRef CAS PubMed.
- See for example: (a) J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358 CrossRef CAS PubMed; (b) R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS; (c) R. A. Marcus, Angew. Chem., Int. Ed. Engl., 1993, 32, 1111 CrossRef.
- See for example: (a) C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. B, 2011, 115, 12234 CrossRef CAS PubMed; (b) C. Iuga, J. R. Alvarez-Idaboy and N. Russo, J. Org. Chem., 2012, 77, 3868 CrossRef CAS PubMed.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334 CrossRef CAS.
- M. E. Alberto, N. Russo, A. Grand and A. Galano, Phys. Chem. Chem. Phys., 2013, 15, 4642 RSC.
- A. Galano and M. Francisco-Márquez, J. Phys. Chem. B, 2009, 113, 16077 CrossRef CAS PubMed.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. B, 2011, 115, 12234 CrossRef CAS PubMed.
- A. Galano, M. Francisco-Márquez and J. R. Alvarez-Idaboy, J. Phys. Chem. B, 2011, 115, 8590 CrossRef CAS PubMed.
- A. Galano and J. R. Alvarez-Idaboy, RSC Adv., 2011, 1, 1763 RSC.
- A. Galano, J. R. Alvarez-Idaboy and M. Francisco-Marquez, J. Phys. Chem. B, 2011, 115, 13101 CrossRef CAS PubMed.
- M. E. Medina, C. Iuga and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2013, 15, 13137 RSC.
- M. E. Medina, C. Iuga and J. R. Alvarez-Idaboy, RSC Adv., 2014, 4, 52920 RSC.
| This journal is © The Royal Society of Chemistry 2015 |