Coupled effects of hydrophobic layer and vibration on thermal efficiency of two-phase closed thermosyphons
Wei Li Tonga,
Ming K. Tana,
Jit Kai Chinb,
K. S. Ongc and
Yew Mun Hung*a
aSchool of Engineering, Monash University, 46150 Bandar Sunway, Malaysia. E-mail: hung.yew.mun@monash.edu
bFaculty of Engineering, University of Nottingham Malaysia Campus, Jalan Broga, 43500 Semenyih, Selangor, Malaysia
cFaculty of Engineering and Green Technology, Universiti Tunku Abdul Rahman, 31900 Kampar, Perak, Malaysia
First published on 6th January 2015
Abstract
Condensed droplets in a two-phase closed thermosyphon (TPCT) are subject to two competing forces: contact line pinning force between the droplet and the wall of the TPCT and the body force due to gravity. Either reducing the contact line pinning force or increasing the body force can lead to significant enhancement in the heat transport capability. This study aims to scrutinize the coupled effects of hydrophobic surface coating at the condenser wall and high-acceleration induced vibration on the thermal efficiency of a TPCT. We explore an approach to reduce the contact line pinning force by applying a thin layer of hydrophobic coating, which also facilitates dropwise condensation to further increase the heat transport capability. The body force of the condensed droplets can be increased by introducing a low-frequency (f ∼ 102 Hz) high-acceleration (![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ∼ 103 m s−2) vibration. The formation of elongated liquid jets and entrainment of droplets induced by the high-acceleration vibration counteracts the enhancing effect from the increased body force of condensed droplets. Nanofluid with distinguished thermo-physical properties is charged to the TPCT to further enhance the thermal efficiency. By incorporating the coupled effects of hydrophobic layer and vibration, we can obtain a maximum augmentation in the heat transfer coefficient exceeding 47.7%. The factors contributing to the enhancement of thermal efficiency of a TPCT are identified and the underlying physical significance of the coupled effects is delineated.
∼ 103 m s−2) vibration. The formation of elongated liquid jets and entrainment of droplets induced by the high-acceleration vibration counteracts the enhancing effect from the increased body force of condensed droplets. Nanofluid with distinguished thermo-physical properties is charged to the TPCT to further enhance the thermal efficiency. By incorporating the coupled effects of hydrophobic layer and vibration, we can obtain a maximum augmentation in the heat transfer coefficient exceeding 47.7%. The factors contributing to the enhancement of thermal efficiency of a TPCT are identified and the underlying physical significance of the coupled effects is delineated.
Introduction
Since its inception in the early twentieth century, two-phase closed thermosyphon (TPCT) has been employed extensively in cooling or heating related applications due to its effective heat transport capability, passive operation, and, also its simplicity in design and operation.1 This two-phase heat transfer device offers significant advantages over other cooling devices, providing an economical yet reliable solution to the demanding heat removal challenges in thermal management. Typical terrestrial applications of TPCT range from the cooling of automobile engines, heat exchanger of solar heating system and industrial refrigeration system to electronics cooling for computer processors. Essentially, a basic TPCT consists of a tube filled with a working fluid in low-pressure (vacuum) condition to reduce saturation temperature. The tube is divided into three sections: evaporator, adiabatic section, and condenser. It relies on the phase-change processes, namely evaporation and condensation, and the circulation of working fluid to function as heat transfer equipment. The heat applied to the evaporator section diffuses toward the liquid–vapor interface where it is taken up as the latent heat of evaporation by the liquid phase. The resultant vapor flows through the adiabatic section toward the condenser section, where the vapor condenses and the heat is dissipated to the surroundings. The thermal efficiency of a TCPT is governed by several pertinent parameters such as the fluid properties and the filling ratio of the working fluid,2,3 evaporator to condenser length ratio,4 inclination angle,5 operating limitations6 and the structure geometry.7 On the other hand, the maximum heat transport capacity of a thermosyphon can be limited by a number of operating limitations such as dry-out limit, burn-out or boiling limit, sonic limit and entrainment limit.8–10Condensation occurs at the saturation temperature when the vapor comes into contact with a cool surface at the condenser section where the condensate is formed. The latent heat of vaporization is released through the condenser wall surface. Depending on the condition of the surface, condensation may occur either in filmwise or dropwise mode. Film condensation primarily takes place on clean and uncontaminated surfaces while dropwise condensation materializes on non-wettable surfaces.11 Dropwise condensation is superior to film condensation as the heat transfer rate of the former is more than an order of magnitude larger than that of the latter.11–13 The condensation in TPCT is a typical example of film condensation where thick liquid condensate layers cover the surface, incurring a larger thermal resistance to heat transfer between the vapor and the surface.4,14 It is a common practice to utilize non-wettable (hydrophobic) surface coating with low surface energy to promote dropwise condensation. A multistage process is involved in the mechanism of dropwise condensation which includes nucleation of initial droplet, droplet growth, droplets coalesce, departure of droplet and coalesce of more droplets as the droplet sweeps downward.15 The enhancement of surface refreshment rate and droplet removal stimulates continuous condensation and consequently augments both the heat and mass transfer coefficients.16 Therefore, it is desirable to achieve dropwise condensation on the condenser surface of a TPCT for thermal efficiency enhancement.
The sustained evaporation of liquid in a TPCT is replenished by the circulation of condensate from the condenser section. A deficient circulation rate induces the occurrence of flooding at the condenser section, impeding the performance of TPCT. The flooding phenomenon in TPCT has been extensively investigated.17–19 Major factors such as heat input, thermo-physical properties of the vapor, vapor velocity and the critical aspect ratio (defined as the radius over length) incur adverse effect on the circulation of the condensates.18,19 Under high evaporation rate, extreme vapor velocity, and small critical aspect ratio, the countercurrent interfacial shear acting on the condensate surface prevents the circulation back to the evaporator. As a result, accumulation of condensate in the condenser greatly reduces the condensation heat transfer. The evaporator section is subsequently depleted with working fluid. Thus, circulation of the condensate is vitally important in the heat transfer mechanism of TPCTs.
As the condensed liquids accumulate and increase in size at the condenser, two dominant competing forces – body force Fb and contact force Fc – exert on these condensed liquids. The bond number, Bo ≡ Fb/Fc, is used to characterize this force balance. When the body force becomes larger than the contact line pinning, i.e., Fb > Fc or Bo > 1, the condensed liquids fall to the evaporator, completing a loop circulation from evaporator to condenser. There have been many attempts to enhance the circulation of the working fluid. For instance, wick structure can be inserted in the TPCT to assist the flow of condensed liquids via capillary force. Alternatively, the circulation rate can be improved by introducing centrifugal force,20,21 electro-kinetic force,22,23 magnetic force,24 or, vibration force.25 Amongst these approaches, inducing vibration on the TPCT is considered the most convenient approach to integrate with the conventional TPCT design. By inducing vibrations, the body force of the condensed liquids is increased due to the increase in acceleration, i.e., Fb ∝ mf![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) , where mf is the mass of the fluids/droplets, and
, where mf is the mass of the fluids/droplets, and ![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) is the acceleration. However, very few prior studies dealt explicitly with the effect of vibration on the circulation effectiveness of a TPCT. Up to date, the only relevant study was focused on low-frequency vibrations (f ∼ 100 Hz).25 While improved performance was observed, the increase of body force exerted on the liquids was only in a very small order of magnitude as a result of accelerations in the order of
is the acceleration. However, very few prior studies dealt explicitly with the effect of vibration on the circulation effectiveness of a TPCT. Up to date, the only relevant study was focused on low-frequency vibrations (f ∼ 100 Hz).25 While improved performance was observed, the increase of body force exerted on the liquids was only in a very small order of magnitude as a result of accelerations in the order of ![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ∼ 10−3 m s−2.
∼ 10−3 m s−2.
This study aims to scrutinize the combined effects of hydrophobic surface coating at the condenser wall and high-acceleration induced vibration (![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ∼ 103 m s−2) on the thermal efficiency of a mini TPCT for electronic equipment cooling. As both approaches reduce the contact forces between the condensed liquids and the TPCT wall, the circulation effectiveness inside a TPCT is expected to be substantially enhanced. We propose a well-defined parameter for the falling rate of condensed droplets and the strength of evaporation to elucidate their relationship. To ensure these approaches are working on different working fluids, water and silver-oxide nanofluid are employed. The use of nanofluid, which is essentially a base fluid with nanoparticle suspension,26 has been reported to be able to enhance the heat transfer characteristic of the conventional fluids.27,28 Nanofluid poses distinct thermal and hydrodynamic characteristics from the conventional fluid associated with its distinguished transport properties such as thermal conductivity, heat capacity, viscosity and surface tension. It is instructive to investigate the coupled effects of the hydrophobic surface at condenser wall and the high-acceleration induced vibration on the nanofluid judging from the prominent changes induced in its thermo-physical properties. In this study, imperative information is obtained from the exposition of the size and distribution of condensate droplets in the analysis of circulation effectiveness. The underlying physical significance of the coupled effects of hydrophobic layer and vibration on the thermal efficiency is outlined.
∼ 103 m s−2) on the thermal efficiency of a mini TPCT for electronic equipment cooling. As both approaches reduce the contact forces between the condensed liquids and the TPCT wall, the circulation effectiveness inside a TPCT is expected to be substantially enhanced. We propose a well-defined parameter for the falling rate of condensed droplets and the strength of evaporation to elucidate their relationship. To ensure these approaches are working on different working fluids, water and silver-oxide nanofluid are employed. The use of nanofluid, which is essentially a base fluid with nanoparticle suspension,26 has been reported to be able to enhance the heat transfer characteristic of the conventional fluids.27,28 Nanofluid poses distinct thermal and hydrodynamic characteristics from the conventional fluid associated with its distinguished transport properties such as thermal conductivity, heat capacity, viscosity and surface tension. It is instructive to investigate the coupled effects of the hydrophobic surface at condenser wall and the high-acceleration induced vibration on the nanofluid judging from the prominent changes induced in its thermo-physical properties. In this study, imperative information is obtained from the exposition of the size and distribution of condensate droplets in the analysis of circulation effectiveness. The underlying physical significance of the coupled effects of hydrophobic layer and vibration on the thermal efficiency is outlined.
Experimental investigation
Preparation of hydrophobic coating
Teflon AF-1600 amorphous fluoroplastics which was purchased from DuPont, Inc. is used to form a hydrophobic layer in TPCT. The hydrophobic coating is deposited onto the inner section of a standard glass tube via spin-coating technique to assure the uniformity of the coating. A total of 10 millilitres of Teflon solution is gently flushed through the glass tube which is then spin coated at a constant speed of 1500 rpm for 30 minutes. Subsequently, the coated glass tube is heated in a furnace with a gradual increase in temperature to a maximum of 250 °C for 30 minutes. Finally, a uniform thin transparent layer of hydrophobic coating on the inner wall surface of TPCT is obtained.Experimental setup
A schematic diagram of the experimental setup is illustrated in Fig. 1. The setup includes a mini TPCT, electrical heater, water cooling jacket, vibrator and measuring instruments. The TPCT is fabricated with a glass tube of inner diameter of di = 13.5 mm and length of L = 110 mm. The glass tube is sealed by using a rubber stopper connected with an access valve for charging of working fluid into the tube [see Fig. 1(a)]. To ensure the TPCT is airtight, epoxy is applied at all connections. | ||
| Fig. 1 (a) Schematic diagram of the basic components of a two-phase closed thermosyphon (TPCT). (b) Experimental setup for the thermal efficiency evaluation of TPCT. | ||
Two different types of working fluid are selected: distilled water and a nanofluid. For nanofluid preparation, silver-oxide (Ag2O) nanoparticles (Sigma-Aldrich, Inc.) with an average particle size of 30 nm and volume fraction of 1% are dispersed in deionized water under mild ultrasonication treatment. The mixtures are ultrasonicated (20 kHz, 700 W) with an ultrasonic processor (Q700 Sonicator®, Qsonica, LLC.) for 5 hours with fluid temperature maintained below 80 °C to prevent evaporation. The TPCT is charged with 1 ml of working fluid, which is equivalent to 16.67% of volume fill ratio. It is a common practice to charge the TPCT with a volume fill ratio which is in the range of 13.5–20%.2,29 This range of fill ratio is considered as the optimal fill ratio in which case there is neither dryout nor flooding taking place in the TPCT. Once the working fluid is charged into the tube, the pressure within the tube is reduced using a vacuum pump, which is connected to the access valve, as shown in Fig. 1(a). The pressure in the tube prior to heating is maintained at 0.2 Pa for all tests. The evaporator section is heated with an electrical heating element, whereas the condenser section is cooled with a water cooling jacket, as depicted in Fig. 1(b).
The experiments are conducted in a controlled environment with a room temperature maintained at 26 °C with a fluctuation of ±1.5 °C. Power input to the electrical heater is controlled by a DC power supply (EA-PSI 8160-04 LCD, EA Elektro-Automatik). Surface temperature on the TPCT is measured using six type-T thermocouple wires with an overall accuracy of 2%, which are connected to a MIDI logger (GL820, Graphtec Co.), with an accuracy of 0.05%. Fig. 1(a) shows the locations of the thermocouple wires. For each test, the temperatures are recorded for 60 minutes, with an interval of two seconds between each recording. To investigate the effect of vibrations, the TPCT is positioned on a vibrating plate excited by a speaker (vibrator), which is connected to an amplifier and a function generator, as shown in Fig. 1(b). The TPCT is placed atop a thin plate attached to a speaker (TD 8′′, Motivity®), to provide lateral vibration to the system. The signal generated by the function generator (TG5011, Thurlby Thandar Instruments limited) is amplified by an amplifier (LZY-22, Mini-Circuits®) before it is transmitted to the speaker. The frequency of excitation is 63 Hz.
Thermal efficiency of TPCT
The thermal efficiency of a TPCT is governed by the circulation effectiveness and the strength of latent heat of evaporation of the working fluid. The thermal efficiency of a TPCT can be quantified with the performance indicators such as the effective thermal resistance Reff and the average evaporator heat transfer coefficient![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) e. Lower thermal resistance indicates better overall thermal performance while larger value of evaporator heat transfer coefficient manifests higher strength of latent heat of evaporation. The overall thermal performance can be characterized using the effective thermal resistance which is obtained by evaluating the axial temperature drop, ΔT = Tevap − Tcond, along the longitudinal direction of TPCT for a heat input. The effective thermal resistance is calculated as:
e. Lower thermal resistance indicates better overall thermal performance while larger value of evaporator heat transfer coefficient manifests higher strength of latent heat of evaporation. The overall thermal performance can be characterized using the effective thermal resistance which is obtained by evaluating the axial temperature drop, ΔT = Tevap − Tcond, along the longitudinal direction of TPCT for a heat input. The effective thermal resistance is calculated as:
 | (1) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a is the heat transport rate of the TPCT. Notably, Tcond is taken here as the averaged temperatures measured across the condenser section. The heat transport rate,
a is the heat transport rate of the TPCT. Notably, Tcond is taken here as the averaged temperatures measured across the condenser section. The heat transport rate, ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a, which is calculated based on the principle of energy conservation whereby the net heat transported across the TPCT is equivalent to the heat dissipated from the condenser section. The total convection heat transfer of the water flowing across the water jacket is determined as
a, which is calculated based on the principle of energy conservation whereby the net heat transported across the TPCT is equivalent to the heat dissipated from the condenser section. The total convection heat transfer of the water flowing across the water jacket is determined as ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a = ṁcp(To − Ti), where ṁ represents the mass flow rate of the water flow, cp is the specific heat capacity of water. Ti and To denote the inlet and outlet water temperatures of the cooling jacket mounted onto the condenser section.
a = ṁcp(To − Ti), where ṁ represents the mass flow rate of the water flow, cp is the specific heat capacity of water. Ti and To denote the inlet and outlet water temperatures of the cooling jacket mounted onto the condenser section.
The average evaporator heat transfer coefficient, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) e, is used to quantify the strength of evaporation, given by
e, is used to quantify the strength of evaporation, given by ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) e =
e = ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a/πdLe(Tevap − Tsat), where Tsat is the saturation temperature of the working fluid, d is the inner diameter of the TPCT and Le is the axial length of the evaporator section. During the experiments, the heat input is kept at a constant value and the evaporator heat transfer coefficient augmentation ratio can be expressed as:
a/πdLe(Tevap − Tsat), where Tsat is the saturation temperature of the working fluid, d is the inner diameter of the TPCT and Le is the axial length of the evaporator section. During the experiments, the heat input is kept at a constant value and the evaporator heat transfer coefficient augmentation ratio can be expressed as:
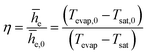 | (2) |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) e,0 is the average evaporator heat transfer coefficient for the case of uncoated TPCT using water as working fluid. To scrutinize the heat transfer enhancement at the evaporator section, η is the relative comparison of the evaporator heat transfer coefficients by using the value of uncoated TPCT as the basis for comparison. The heat transfer is enhanced when η is greater than unity and vice versa.
e,0 is the average evaporator heat transfer coefficient for the case of uncoated TPCT using water as working fluid. To scrutinize the heat transfer enhancement at the evaporator section, η is the relative comparison of the evaporator heat transfer coefficients by using the value of uncoated TPCT as the basis for comparison. The heat transfer is enhanced when η is greater than unity and vice versa.
Evaluation of static contact angle
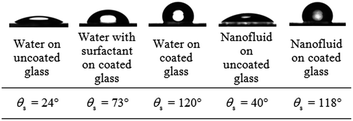
The static contact angle θs between the liquid and the substrate under different conditions are measured using a standard goniometer (Model 590, Ramé-Hart Instrument Co.) under atmospheric pressure and a room temperature of 26 °C. Table 1 shows the results of the contact angle measurements under different conditions. For glass coated with a thin hydrophobic layer, the contact angle is slightly lower for nanofluid (θs ≈ 118°) as compared to the distilled water (θs ≈ 120°). With the addition of surfactant to the distilled water on the hydrophobic surface, the static contact angle decreases (θs ≈ 73°). The reduction in static contact angle of the nanofluid was studied by Wasan and Nikolov.30 It was found that the nanoparticles near the liquid-contact line tend to increase the spreading of the nanofluid, resulting in the decrease of the static contact angle.Results and discussion
Effect of hydrophobic surface
Fig. 2 shows the plots of the effective thermal resistances Reff as a function of heat transport rate,![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a, for three different contact forces between the working fluid and the TPCT wall: water on bare glass (θs ≈ 24°), water added with surfactant on coated glass (θs ≈ 73°), and, water on coated glass (θs ≈ 120°), representing the cases for high, mid, and low contact force, respectively. In the cases of low and mid contact force, Reff is lower compared to that of high contact force. At
a, for three different contact forces between the working fluid and the TPCT wall: water on bare glass (θs ≈ 24°), water added with surfactant on coated glass (θs ≈ 73°), and, water on coated glass (θs ≈ 120°), representing the cases for high, mid, and low contact force, respectively. In the cases of low and mid contact force, Reff is lower compared to that of high contact force. At ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a = 15.5 W, for the cases of low and mid contact force, Reff records a reduction of 16.9% and 11.4%, respectively. A smaller Reff indicates a higher heat transport capability of the TPCT. The reduction in the Reff can be attributed to the presence of hydrophobic coating that lowers the contact force Fc, which then facilitates the falling of condensed droplets back to the evaporator. It is observed that by reducing the contact force Fc between the condensed droplets and the wall of TPCT, the effective thermal resistance Reff is further reduced due to the enhanced circulation of the working fluid.
a = 15.5 W, for the cases of low and mid contact force, Reff records a reduction of 16.9% and 11.4%, respectively. A smaller Reff indicates a higher heat transport capability of the TPCT. The reduction in the Reff can be attributed to the presence of hydrophobic coating that lowers the contact force Fc, which then facilitates the falling of condensed droplets back to the evaporator. It is observed that by reducing the contact force Fc between the condensed droplets and the wall of TPCT, the effective thermal resistance Reff is further reduced due to the enhanced circulation of the working fluid.
On the other hand, the strength of evaporation is observed to be indirectly affected by the contact force, as shown in Fig. 3, which depicts the evaporator heat transfer coefficient augmentation ratios η for two cases: water added with surfactant on coated glass (θs ≈ 73°), and, water on coated glass (θs ≈ 120°), using the case of water on bare glass (θs ≈ 24°) as the baseline for comparison. For the range of heat transport rate under investigation, we can observe that the enhancement of heat transfer coefficient increases with the decrease in the contact force. For the case of smaller contact force (water on coated glass), the enhancement in the heat transfer coefficient can exceed 20.4% at high heat transport rate. It is shown that the enhancement in circulation effectiveness and strength of evaporation is inherently simultaneous.
The size and distribution of the droplets are important factors in governing the mechanism of condensation heat transfer in a TPCT. We shall, therefore, be concerned with the size and distribution of the droplets in the following. Fig. 4(a) and (b) show the time-lapse images of the morphology of condensed droplets on the interior wall of the uncoated and coated TPCT with the hydrophobic layer, respectively. Evidently, the diameters of the condensed droplets on the coated glass tube are observed to be significantly smaller than those on the uncoated glass. We also note that dropwise condensation is prevalent in the former while film condensation occurs in the latter. As observed in Fig. 4(b) for dropwise condensation, when the droplet size increases to a diameter of 650 μm (as indicated with an arrow), the droplet starts to detach from the wall surface and move downwards coalescing with other droplets. The sliding speed increases as more droplets are combined. Subsequently, nucleation of new droplets can be observed as illustrated in the dashed circles. This shows that the surface refreshment rate (departure rate of condensed droplets on a hydrophobic surface) is high, allowing a continuous dropwise condensation to occur on the wall surface. On the contrary, Fig. 4(a) illustrates the droplet growth cycle of an uncoated glass surface. The departure diameter is found to be larger than that of the hydrophobic surface. The largest droplet diameter is measured to be more than 2500 μm with no sign of droplet departure. It has been shown that the typical droplet departure diameter on an uncoated glass surface under film condensation is between 2 mm to 3 mm.12 Continuous coalescence of neighbouring droplets forms non-circular droplets, indicating a weak three-phase contact line with a large contact angle hysteresis.31,32 The large droplets on the wall surface form a thermal barrier which inhibits the condensation of the vapour, and hence reducing the overall condensing heat transfer coefficient. Furthermore, large droplets which occupy the surface reduce the area for vapour condensation, hindering the droplet growth rate in a TPCT.
 | ||
| Fig. 4 Time-lapse images of the morphology of condensed droplets on the interior wall of the (a) uncoated TPCT, and, (b) coated TPCT. | ||
To have a detailed view on the size and distribution of droplets on the mechanism of condensation, we quantify the average diameter range and the number of droplets condensing on the TPCT wall surface. SigmaScan® Pro (Systat Software, CA, USA) is used for image processing and analysis of droplet distribution and droplet size. Fig. 5(a) and (b) depict the average droplet count, N, as a function of droplet diameter, D, for the uncoated and coated surfaces, respectively. The diameters of the condensed droplets on the uncoated glass tube (100 μm–2500 μm) are observed to be significantly larger than those on the coated glass (50 μm–650 μm).
 | ||
| Fig. 5 Average droplet count, N, as a function of droplet diameter, D, for the (a) uncoated and (b) coated surfaces. | ||
To scrutinize the droplet distribution over the entire wall surface of the condenser, we use the total surface area of condenser as the basis for comparison. A relative comparison parameter between the covering surface area of droplet, Ad, and the total surface area, At, is quantified as δ = Ad/At. The δ value is evaluated by analyzing the marked surface area covered by the droplets on the condenser wall using SigmaScan® Pro image processing software. At a fixed heat transport rate of 15.5 W, high definition images are taken continuously for every minute during the steady state of the experiments. To ensure the accuracy of the measurement of randomly distributed droplets on the surface, a total of 24 images from 3 independent sets of experiment are analyzed. The surface area covered by the droplets, Ad, on a specific region on the condenser wall with an area of At = 10 mm × 10 mm, is marked. By setting a reference length scale, SigmaScan® Pro is used to measure the total surface area covered by the droplets. The δ value is calculated based on the statistical mean of a sample size of 24. It is found that at an instant of steady operation of a TPCT, we measure δ = 33.7% for the coated hydrophobic surface and δ = 67.7% for the uncoated surface. This attests the fact that the hydrophobic surface which repels water molecules yields higher circulation rate for the condensate from the condenser to the evaporator. In addition, the hydrophobic surface provides larger liquid-free and sub-cooled surface for nucleation of new droplets and hence the condensation rate is enhanced.
As the condensate liquids accumulate and increase in size at the condenser, two dominant competing forces - body force Fb and the contact line pinning force Fc exert on these condensed liquids. The shear force at the liquid–vapor interface Fs is assumed to be negligible. This point has been justified by comparing the order of magnitude of the interfacial shear force and that of the body force in an independent set of experiments. By virtue of low relative velocities associated with the vapor flow and the droplet motion, it is found that the body force Fb is at least 104 times of the shear force Fs. Therefore, together with the assumption of a uniform vapor temperature, the interfacial shear force acting on the surface of the liquid droplet can be neglected. To characterize the two dominant forces acting on a droplet, the bond number is used and it is given by Bo ≡ ρlg![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/γ(cos
2/γ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA − cosθR) ≡ Fb/Fc, where ρl is the liquid density, g is the gravitational acceleration,
θA − cosθR) ≡ Fb/Fc, where ρl is the liquid density, g is the gravitational acceleration, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the characteristic length defined as the radius of droplet, γ is the coefficient of interfacial surface tension, θA is the advancing contact angle and θR is the receding contact angle of the droplet. When the body force becomes larger than the contact line pinning force, i.e., Fb > Fc or Bo > 1, the condensed liquids fall to the evaporator, completing a loop circulation from evaporator to condenser. The contact line pinning force increases with the decrease of contact angle. The decrease in static contact angle greatly affects the dynamic behavior of the droplet. The contact line of the three phases (solid, liquid, and vapor) deteriorates with the decrease of the static contact angle, increasing the contact area of the droplet.31 As a result, the contact line can be easily deformed, resulting in an increase of contact angle hysteresis. Contact angle hysteresis is defined as the difference between the advancing and the receding angles. High contact angle hysteresis impedes the movement of the droplet and higher external force is required for the droplet to overcome the pinning force Fc. Hence, for the droplet to depart, accumulation in size is required to increase the body force Fb. As noted earlier that Bo ≡ Fb/Fc and the liquids start to fall back to the evaporator when Fb > Fc. Therefore, by reducing the Fc, the condensed droplets begin to fall back to the evaporator at a smaller body force. Since the body force is directly proportional to the volume of the condensed liquid, i.e., Fb = mg = ρVg, for the TPCT coated with the hydrophobic layer, the diameter of the condensed droplets should be much smaller than those without coating. This is consistent with the experimental images shown in Fig. 4 for condensed droplets on the interior wall of the TPCT with and without the hydrophobic coating. The diameters of the condensed droplets on the uncoated glass tube are observed to be significantly larger (100 μm–2500 μm) than those on the coated glass (50 μm–650 μm), inferring that the former is film condensation whereas the latter is dropwise condensation. For film condensation, a thick layer of condensed liquid covers the wall surface, lowering the heat transfer rate. On the other hand, dropwise condensation allows for more continuous condensation to occur on the wall surface. This in turn results in high surface refreshment rate, i.e. the departure rate of condensed droplets, thereby improving the resultant heat transfer rate. It has been shown that the heat transfer coefficient for dropwise condensation is an order of magnitude higher than that for film condensation.12 Therefore, the hydrophobic surface not only improves the circulation by increasing the falling rate of condensed droplets, it also facilitates the formation of dropwise condensation, which further improves the heat transport capability of the TPCT.
is the characteristic length defined as the radius of droplet, γ is the coefficient of interfacial surface tension, θA is the advancing contact angle and θR is the receding contact angle of the droplet. When the body force becomes larger than the contact line pinning force, i.e., Fb > Fc or Bo > 1, the condensed liquids fall to the evaporator, completing a loop circulation from evaporator to condenser. The contact line pinning force increases with the decrease of contact angle. The decrease in static contact angle greatly affects the dynamic behavior of the droplet. The contact line of the three phases (solid, liquid, and vapor) deteriorates with the decrease of the static contact angle, increasing the contact area of the droplet.31 As a result, the contact line can be easily deformed, resulting in an increase of contact angle hysteresis. Contact angle hysteresis is defined as the difference between the advancing and the receding angles. High contact angle hysteresis impedes the movement of the droplet and higher external force is required for the droplet to overcome the pinning force Fc. Hence, for the droplet to depart, accumulation in size is required to increase the body force Fb. As noted earlier that Bo ≡ Fb/Fc and the liquids start to fall back to the evaporator when Fb > Fc. Therefore, by reducing the Fc, the condensed droplets begin to fall back to the evaporator at a smaller body force. Since the body force is directly proportional to the volume of the condensed liquid, i.e., Fb = mg = ρVg, for the TPCT coated with the hydrophobic layer, the diameter of the condensed droplets should be much smaller than those without coating. This is consistent with the experimental images shown in Fig. 4 for condensed droplets on the interior wall of the TPCT with and without the hydrophobic coating. The diameters of the condensed droplets on the uncoated glass tube are observed to be significantly larger (100 μm–2500 μm) than those on the coated glass (50 μm–650 μm), inferring that the former is film condensation whereas the latter is dropwise condensation. For film condensation, a thick layer of condensed liquid covers the wall surface, lowering the heat transfer rate. On the other hand, dropwise condensation allows for more continuous condensation to occur on the wall surface. This in turn results in high surface refreshment rate, i.e. the departure rate of condensed droplets, thereby improving the resultant heat transfer rate. It has been shown that the heat transfer coefficient for dropwise condensation is an order of magnitude higher than that for film condensation.12 Therefore, the hydrophobic surface not only improves the circulation by increasing the falling rate of condensed droplets, it also facilitates the formation of dropwise condensation, which further improves the heat transport capability of the TPCT.
To elucidate the relationship of the falling rate of condensed droplets and the strength of evaporation, in the uncoated and coated TPCT, we recast the experimental data in terms of a new dimensionless number
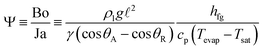 | (3) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) a for uncoated and coated TPCTs are shown in Fig. 6. At each fixed heat transport rate, the Ψ for the coated (hydrophobic) TPCT is higher than that for the uncoated (hydrophilic) TPCT, indicating the falling rate of condensed droplets in the coated TPCT is higher than that in the uncoated TPCT. On the other hand, as the heat transport rate is proportional to the heat input power of the heater, for both uncoated and coated TPCT, the Ψ reduces with the increase of the heat input power due to the increase in the evaporation rate (higher Ja).
a for uncoated and coated TPCTs are shown in Fig. 6. At each fixed heat transport rate, the Ψ for the coated (hydrophobic) TPCT is higher than that for the uncoated (hydrophilic) TPCT, indicating the falling rate of condensed droplets in the coated TPCT is higher than that in the uncoated TPCT. On the other hand, as the heat transport rate is proportional to the heat input power of the heater, for both uncoated and coated TPCT, the Ψ reduces with the increase of the heat input power due to the increase in the evaporation rate (higher Ja).
Coupled effects of hydrophobic surface and high-acceleration vibration
As discussed earlier, to further increase the circulation rate, we can either reduce the contact force Fc by introducing a thin layer of hydrophobic coating (Fig. 2), or, increase the body force Fb by inducing vibrations. Fig. 7 shows the experimental results of the effect of vibrations on the effective thermal resistance. The results show that for all cases, the effective thermal resistance Reff is reduced once the vibration is introduced. The reduction in Reff is within the range of 1.9–5.8% for uncoated hydrophilic TPCT, as depicted in Fig. 7(a). Interestingly, for coated hydrophobic TPCT shown in Fig. 7(b), the reduction in Reff which ranges from 5.2% to 21.9% is almost triple to that of the uncoated TPCT. The reduction in Reff is attributed to the increase in the rate of falling of condensed droplets to the evaporator. When the TPCT tube is subjected to vibratory force, the body force increases due to the additional acceleration generated by the vibrating plate, i.e., Fb ≈ m(g +![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ). For a 63 Hz excitation with surface displacement in the order of 10−3 m, the estimated surface acceleration is in the order of
). For a 63 Hz excitation with surface displacement in the order of 10−3 m, the estimated surface acceleration is in the order of ![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ∼ 103 m s−2, which is two order of magnitudes higher than the gravitational acceleration g ∼ 101 m s−2, therefore the falling rate of droplets is enhanced. As these droplets slide along the condenser wall, more liquid-free sub-cooled surfaces are available for the nucleation of new condensate droplets. In light of its distinguished thermophysical properties, Ag2O-water nanofluid is also used as a working fluid in the uncoated and coated TPCTs. The results demonstrate a similar trend of improvement, as shown in Fig. 7(a) and (b). Under similar experiment conditions (uncoated with vibration), the TPCT filled with nanofluid as working fluid has lower thermal resistance as compared to the TPCT filled with water; the reduction in thermal resistance is in the range of 18.3–21.2%.
∼ 103 m s−2, which is two order of magnitudes higher than the gravitational acceleration g ∼ 101 m s−2, therefore the falling rate of droplets is enhanced. As these droplets slide along the condenser wall, more liquid-free sub-cooled surfaces are available for the nucleation of new condensate droplets. In light of its distinguished thermophysical properties, Ag2O-water nanofluid is also used as a working fluid in the uncoated and coated TPCTs. The results demonstrate a similar trend of improvement, as shown in Fig. 7(a) and (b). Under similar experiment conditions (uncoated with vibration), the TPCT filled with nanofluid as working fluid has lower thermal resistance as compared to the TPCT filled with water; the reduction in thermal resistance is in the range of 18.3–21.2%.
 | ||
| Fig. 7 Effect of vibration on the effective thermal resistance of (a) uncoated TPCT and (b) coated TPCT using water and nanofluid as working fluid. | ||
The effect of vibration on the strength of evaporation is investigated and the evaporator heat transfer coefficient augmentation ratios are evaluated using eqn (2) and plotted as a function of heat transport rate for both uncoated and coated TPCTs in Fig. 8. As discussed earlier, the contact force between the droplets and the condenser wall is associated with the circulation effectiveness of condensate. We observe that the effect of vibration on the strength of evaporation is also prevalent although it is not dominant. This observation is congruous with a recent study investigating the effect of electrically induced droplet oscillation on evaporation.33 However, interestingly, it is observed that the suspension of nanoparticles significantly augments the heat transfer coefficient augmentation ratio which characterizes the strength of evaporation, for both cases without and with vibration. The increases in heat transfer coefficient are observed to exceed 35.2% and 47.7% for the cases without and with vibration, respectively, in a coated TPCT, as depicted in Fig. 8(b). This augmentation is attributed to the deposition of nanoparticles on the evaporator surface which significantly enhances the nucleate boiling mechanism and surface wettability.34–36 The effect of deposition of nanoparticles on the performance enhancement is worth further investigation.
 | ||
| Fig. 8 Effect of vibration on the evaporator heat transfer coefficient augmentation ratios of (a) uncoated TPCT and (b) coated TPCT using water and nanofluid as working fluid. | ||
Despite these favorable factors enhancing the circulation of the condensate, the maximum reductions in thermal resistance Reff are only about 12.1% and 14.3% for water charged TPCT and nanofluid charged TPCT, respectively. It is evident that the effect of vibration on the improvement of overall circulation rate is not as significant as predicted. To investigate the underlying physical justification of the marginal increase in the circulation effectiveness rendered by the high-acceleration vibration, a digital high-speed camera (Phantom Miro M 310, Vision Research™) coupled with a long-distance microscope is employed to record the high-speed events of transient phenomena in the TPCT with particular attention paid to the liquid–vapor interfacial structure. It is observed that in addition to higher body force experienced by the condensed droplets at the evaporator, the high acceleration induced by the vibrator generates elongated liquid jets which subsequently break up into multiple droplets, as illustrated in Fig. 9. The diameter of these droplets is between 2 to 3 mm. Based on the images recorded at 1000 frames per second, the estimated jet Weber number Wej is approximately 100, indicating a strong inertial force dominating the jet motion. The jet Weber number is defined as Wej ≡ ρUj2Rj/γ, where Rj is the radius of the jet, and Uj is the velocity of the jet. The excitation from the vibration induces large surface waves at the liquid–vapor interface at the evaporator section, creating instabilities in the liquid flow. This leads to the formation of elongated liquid jets which eventually break up into finer droplets. The droplets formed from the breakup of the elongated jets are observed to be entrained in the vapor flow and returned to the condenser. This entrainment of liquid droplets induced by the high-acceleration vibration can be analogous to the typical entrainment phenomenon caused by high shear forces developed at the liquid–vapor interface due to the high relative velocity between the counter-current liquid and vapor flows when the axial heat flux imposed on a TPCT is substantially high.8,37,38 The latter which is associated with the entrainment limit in the operation of a TPCT provokes a depletion of liquid supply to the evaporator, incurring a local dry-out at the evaporator and flooding at the condenser if the entrainment is sufficiently intense.8 When the entrained droplets deposit on the condenser wall surface, the thermal resistance increases and the condensation heat transfer deteriorates. Consequently, the axial heat flux and the performance of the TPCT decline. In the present study, the vibration-induced entrainment of droplets acts in a similar manner in returning the liquid back to the condenser, impeding the circulation rate of the condensate. Up to this point, the marginal increase in the circulation effectiveness rendered by the high-acceleration vibration can be reasoned out. The high-acceleration vibration yields two opposing effects on the liquid circulation effectiveness in a TPCT. The increase in the rate of falling of condensed droplets to the evaporator is apparent and explicit while the entrainment of droplets back to the condenser is a subtle phenomenon. The former is viable in enhancing the circulation effectiveness while the latter generates an adverse effect that counteracts with the enhancing effect of the increased falling rate of condensed droplets, inhibiting the circulation rate. The observation of liquid jets and entrained droplets provides valuable experimental insights into the physical process of the liquid–vapor interaction induced by the high-acceleration vibration in a TPCT.
 | ||
| Fig. 9 Elongated liquid jet generated at the evaporator due to the strong vibration. The jet breaks up into multiple finer droplets which are entrained in the vapor flow. | ||
Conclusions
We have studied the effects of contact force and vibration on the thermal efficiency of TPCTs. By comparing the experimental results for uncoated (hydrophilic) glass tube and coated (hydrophobic) glass tube, the reduction in the effective thermal resistance Reff, which is used to characterize the overall thermal performance, is between 3.2% and 16.9%. This reduction is primarily due to the increase in the falling rate of the condensed droplets and the formation of dropwise condensation. The strength of evaporation which is characterized by the evaporator heat transfer coefficient augmentation ratio is observed to be indirectly affected by the contact force. The enhancement in the circulation effectiveness and the strength of evaporation is inherently simultaneous. The high-acceleration vibration (![[greek xi with two dots above]](https://www.rsc.org/images/entities/i_char_e1ae.gif) ∼ 103 m s−2) on the TPCT also reduces the Reff; the reduction is between 1.9% and 5.8%. By combining both the effects of contact force and vibration, the total reduction of Reff is between 5.2% and 21.9%. For nanofluid, the effects of contact force and vibration on the reduction in Reff are similar. However, it is observed that the utilization of nanoparticles substantially increases the heat transfer coefficient augmentation ratios, exceeding 35.2% and 47.7% for the cases without and with vibration, respectively, in a coated TPCT. Interestingly, the observation of elongated liquid jets and entrained droplets from the liquid–vapor interface induced by the high-acceleration vibration delineates the underlying physical justification of the marginal increase in the circulation effectiveness. This observation provides valuable experimental insights into the physical process of the liquid–vapor interaction phenomena induced by the high-acceleration vibration in a TPCT. To eliminate the entrainment of droplets back to the condenser which impedes the circulation rate of the condensate, high-frequency and low-acceleration vibrations (f > 100 kHz) can be employed in the future investigation.
∼ 103 m s−2) on the TPCT also reduces the Reff; the reduction is between 1.9% and 5.8%. By combining both the effects of contact force and vibration, the total reduction of Reff is between 5.2% and 21.9%. For nanofluid, the effects of contact force and vibration on the reduction in Reff are similar. However, it is observed that the utilization of nanoparticles substantially increases the heat transfer coefficient augmentation ratios, exceeding 35.2% and 47.7% for the cases without and with vibration, respectively, in a coated TPCT. Interestingly, the observation of elongated liquid jets and entrained droplets from the liquid–vapor interface induced by the high-acceleration vibration delineates the underlying physical justification of the marginal increase in the circulation effectiveness. This observation provides valuable experimental insights into the physical process of the liquid–vapor interaction phenomena induced by the high-acceleration vibration in a TPCT. To eliminate the entrainment of droplets back to the condenser which impedes the circulation rate of the condensate, high-frequency and low-acceleration vibrations (f > 100 kHz) can be employed in the future investigation.
Acknowledgements
The authors would like to thank the financial support by Green Electronics, Advanced Engineering Platform, Monash University Malaysia.Notes and references
- G. S. H. Lock, The tubular thermosyphon – variation on a theme, Oxford University Press, 1992 Search PubMed.
- B. Jiao, L. M. Qiu, X. B. Zhang and Y. Zhang, Appl. Therm. Eng., 2008, 28, 1417–1426 CrossRef CAS PubMed.
- H. Jouhara and A. J. Robinson, Appl. Therm. Eng., 2010, 30, 201–211 CrossRef CAS PubMed.
- S. H. Noie, Appl. Therm. Eng., 2005, 25, 495–506 CrossRef CAS PubMed.
- H. Jouhara and R. Meskimmon, Energy, 2010, 35, 4592–4599 CrossRef PubMed.
- M. S. El-Genk and H. H. Saber, Int. J. Heat Mass Transfer, 1999, 42, 889–903 CrossRef CAS.
- H. M. S. Hussein, H. H. El-Ghetany and S. A. Nada, Energy Convers. Manage., 2006, 47, 1539–1549 CrossRef CAS PubMed.
- H. Nguyen-Chi and M. Groll, J. Heat Recovery Syst., 1981, 1, 275–286 CrossRef CAS.
- D. Reay and P. Kew, Heatpipes, Theory, Design and Applications, Butterworth-Heinemann, Burlington, 5th edn, 2006 Search PubMed.
- G. P. Peterson, An Introduction to Heat Pipes Modeling, Testing and Applications, John Wiley & Sons Inc., New York, USA, 1994 Search PubMed.
- F. P. Incropera, A. S. Lavine, T. L. Bergman and D. P. DeWitt, Principles of heat and mass transfer, Wiley, 2013 Search PubMed.
- X. Chen, J. Wu, R. Ma, M. Hua, N. Koratkar, S. Yao and Z. Wang, Adv. Funct. Mater., 2011, 21, 4617–4623 CrossRef CAS.
- N. A. Patankar, Soft Matter, 2010, 6, 1613–1620 RSC.
- R. Kempers, A. J. Robinson, D. Ewing and C. Y. Ching, Int. J. Heat Mass Transfer, 2008, 51, 6039–6046 CrossRef PubMed.
- S. Yongji, X. Dunqi, L. Jifang and T. Siexong, Int. J. Heat Mass Transfer, 1991, 34, 2827–2831 CrossRef.
- S. Lee, H. K. Yoon, K. J. Kim, S. Kim, M. Kennedy and B. J. Zhang, Int. J. Heat Mass Transfer, 2013, 60, 664–671 CrossRef PubMed.
- S. J. Chen, J. G. Reed and C. L. Tien, Int. J. Heat Mass Transfer, 1984, 27, 1587–1594 CrossRef CAS.
- U. Gross, Int. J. Heat Mass Transfer, 1992, 35, 279–294 CrossRef CAS.
- Y. Pan, Int. Commun. Heat Mass Transfer, 2001, 28, 311–322 CrossRef CAS.
- N. Waowaew, P. Terdtoon, S. Maezawa, P. Kamonpet and W. Klongpanich, Appl. Therm. Eng., 2003, 23, 1019–1032 CrossRef CAS.
- S. W. Chang and C. Y. Lin, Int. J. Heat Mass Transfer, 2013, 62, 40–54 CrossRef PubMed.
- S. Wangnipparnto, J. Tiansuwan, T. Kiatsiriroat and C. C. Wang, Energy Convers. Manage., 2003, 44, 1163–1175 CrossRef CAS.
- S. Z. Heris, F. Mohammadpur and A. Shakouri, Mater. Res. Bull., 2014, 53, 21–27 CrossRef CAS PubMed.
- E. Fornalik, P. Filar, T. Tagawa, H. Ozoe and J. S. Szmyd, Int. J. Heat Mass Transfer, 2006, 49, 2642–2651 CrossRef CAS PubMed.
- H. Z. Abou-Ziyan, A. Helali, M. Fatouh and M. M. A. El-Nasr, Appl. Therm. Eng., 2001, 21, 813–830 CrossRef CAS.
- S. Chol, Am. Soc. Mech. Eng., 1995, 231, 99–106 Search PubMed.
- S. K. Das, S. U. S. Choi and H. E. Patel, Heat Transfer Eng., 2006, 27, 3–19 CrossRef CAS.
- R. Saidur, K. Leong and H. Mohammad, Renewable Sustainable Energy Rev., 2011, 15, 1646–1668 CrossRef CAS PubMed.
- H. Imura, K. Sasaguchi, H. Kozai and S. Numata, Int. J. Heat Mass Transfer, 1983, 26, 1181–1188 CrossRef CAS.
- D. T. Wasan and A. D. Nikolov, Nature, 2003, 423, 156–159 CrossRef CAS PubMed.
- Z. Yoshimitsu, A. Nakajima, T. Watanabe and K. Hashimoto, Langmuir, 2002, 18, 5818–5822 CrossRef CAS.
- R. Blossey, Nat. Mater., 2003, 2, 301–306 CrossRef CAS PubMed.
- M. Chakraborty, A. Ghosh and S. DasGupta, RSC Adv., 2014, 4, 1074–1082 RSC.
- V. Trisaksri and S. Wongwises, Renewable Sustainable Energy Rev., 2007, 11, 512–523 CrossRef CAS PubMed.
- S. M. You, J. H. Kim and K. H. Kim, Appl. Phys. Lett., 2003, 83, 3374–3376 CrossRef CAS PubMed.
- S. J. Kim, I. C. Bang, J. Buongiorno and L. W. Hu, Appl. Phys. Lett., 2006, 89, 153107 CrossRef PubMed.
- G. Peterson and B. Bage, J. Energy Resour. Technol., 1991, 113, 147–153 CrossRef.
- D. Shatto, J. Besly and G. Peterson, J. Thermophys. Heat Transfer, 1997, 11, 579–581 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |