Anisotropic vacancy-defect-induced fracture strength loss of graphene

Abstract

The mechanical strength of graphene is much larger than any other materials, but is orientation-dependent and can be significantly weakened by vacancy defects existing in the lattices. In this work, we investigated the orientational anisotropic effect on the fracture strength of vacancy-defective graphene using molecular dynamics simulations. The results show that the fracture strength of graphene at the orientation angle of 15° has the smallest sensitivity to vacancy defects due to the minimization of stress concentration in this direction. Although the fracture strength of defect-free graphene in the zigzag direction is larger than that in the armchair direction, the fracture strength in the zigzag direction is much more sensitive to the vacancy defects. This study is helpful not only for understanding the physical properties of defective graphene but also providing guidance for developing graphene-based materials or devices in engineering.

---

1. Introduction

Graphene, a two-dimensional monolayer graphite, has attracted intensive research interest during the past decade owing to its unprecedented mechanical, thermal, electric and optical properties.^1–9 For example, the tensile strength of pristine graphene is over 100 GPa and its Young's modulus can reach up to 1 TPa,^2,3 much stronger than any other materials that have been discovered. The outstanding mechanical properties of graphene have been explored for a broad range of applications such as graphene nanocomposites,⁷ chemical sensors,⁵ supercapacitors,^8,9 surface coatings,⁴ and nanoelectronics.^1,6 However, in preparing the graphene for all these applications, the defects in the graphene lattice, such as vacancy defects,¹⁰ impurity defects,¹¹ and absorption defects,¹² are inevitable due to the production process^13,14 and the environmental/operation conditions.¹⁵ On the other hand, defect engineering of graphene is also employed to modify graphene with novel functions in nanoelectronics and biodevices.^15,16 Therefore, it is of fundamental importance to understand the mechanical properties of defective graphene for developing novel graphene-based materials or devices under various operation conditions.

The failure strength of graphene has been investigated using both experimental and numerical methods, including atomic force microscopy (AFM) nanoindentation,² molecular dynamics (MD) simulation^17,18 and finite element method¹⁹ etc. It has been reported that graphene exhibits distinct anisotropic mechanical behaviors because of its hexagonal network structure.^20–22 Zhao et al.²³ investigated the mechanical strength of graphene under uniaxial tensile test by combining MD simulations and tight-binding (TB) method, and found that the fracture strength of monolayer graphene in zigzag direction is 18.8% larger than that under armchair-directional elongation. Mortazavi et al.²⁴ performed MD simulations to study the orientation-dependency of the fracture property of graphene. Their results have shown that the ultimate tensile strength increases as the loading direction transits from armchair to zigzag direction. Jhon et al.²⁵ systematically studied the fracture behavior of graphene under uniaxial tensile loading in varying directions. They found that as the applied tensile loading rotates by an angle of ∼12° from the armchair (0°) direction, the fracture strength of graphene is almost constant up, and then increase dramatically until the loading direction reaches at the zigzag direction (30°).²⁵

Simulations and quantized fracture mechanics have shown that the fracture strength of graphene is sensitive to vacancy defect and a remarkable loss of fracture strength can be occurred by the presence of vacancy defect.^26–28 However, little is known on the sensitivity of the fracture strength of defective graphene in various directions, and most previous studies on the orientation-dependent fracture behavior of graphene have been mainly devoted to defect-free graphene.^23,25 Therefore, in this letter, we perform MD simulations to study the orientational anisotropic effect on the fracture strength of a monolayer graphene sheet with a central vacancy defect and to explore the underlying deformation mechanism.

2. Methods

The carbon atoms in a graphene sheet are arranged in a honeycomb lattice. As shown in Fig. 1a, the orientation of graphene can be described by a chiral vector C = na₁ + ma₂, where a₁ and a₂ are the unit vectors of the graphene lattice, n and m are two integers.¹⁸ The integer pair (n, m), called the chiral index, defines a chiral vector. Orientation (n, n) and (n, 0) are mapping to the armchair and zigzag direction, respectively. The angle between the armchair direction (n, m) and the arbitrary direction (n, m) is called the orientation angle θ, which is in the range of 0° ≤ θ ≤ 30° due to the six-fold rotation symmetry of the graphene atomic lattice. Thus, the orientation angle θ for the armchair and zigzag directions are 0° and 30°, respectively.

Fig. 1 Simulation model. (a) Orientation of graphene. The orientation angle θ is defined as the angle between the armchair direction and the tensile loading direction. (b) MD model of graphene in uniaxial tension test. The displacement loading condition is applied by stretching the periodic simulation box in the x direction. (c) Enlarged view of boundary. Coordinates of carbon atoms closed to the boundary are discreetly examined to avoid unwanted atom losses or overlaps. (d) Enlarged drawing of vacancy defect, introduced by deleting the carbon atom in the center of graphene sheet.

Here we consider a single graphene sheet with a central vacancy defect for the simulation, as shown in Fig. 1b. The system dimensions of the graphene sheet are L = 200 Å and W = 200 Å. In this work, eleven typical tensile orientations and their corresponding chiral index (n, m), as listed in Table 1, are selected for investigating the orientation dependence of the fracture strength of the defective graphene sheet. We define x-axis along the loading direction, and z-axis normal to the graphene plane. Period boundary conditions are applied in all the three directions to remove boundary effect. Fig. 1c shows the enlarged view of boundary. Coordinates of carbon atoms near the boundary are carefully checked to ensure exactly one atom at the boundaries (on either side of the simulation box), and to avoid unwanted atom overlaps or losses at the boundaries. The enlarged drawing of vacancy defect is depicted in Fig. 1d. Atoms around the vacancy defect are painted as red color. The vacancy defect in the simulation model is generated as follows. Firstly, the coordinates of carbon atoms are checked to seek the center atom; and secondly, this center atom is moved out from the graphene sheet.

Table 1 Typical tensile orientations and their corresponding chiral index

Orientation angle θ (°)	Chiral index (n, m)
0	(1, 1)
3.67	(6, 5)
5.82	(10, 7)
8.95	(7, 4)
12.01	(13, 6)
14.70	(8, 3)
17.78	(7, 2)
21.05	(5, 1)
23.82	(15, 2)
27.00	(16, 1)
30	(1, 0)

---

We perform MD simulations using LAMMPS package with the adaptive interatomic reactive empirical bond-order (AIREBO)²⁹ potential. This potential has been demonstrated to be quite useful in describing the interactions of carbon atoms in the graphene or other carbon materials.^30,31 In LAMMPS, the default value of C–C bond cutoff distance in the switching function for the AIREBO potential is 1.70 Å. Using such a cutoff distance, however, may result in unphysical simulation results, e.g. higher bond forces before cracking.²³ Thus, to avoid spurious post-hardening mechanical behaviors, Jhon et al.²⁵ adjusted the cutoff distance in AIREBO potential to 2.0 Å, and Carpenter et al.²⁶ selected the cut-off distance to be 1.92 Å. Recently, He et al.³² systematically studied the relationship between the tensile strength and C–C bond cutoff distance in MD simulation of graphene, and finally selected the cut-off distance of 1.95 Å. In this work, we select the same value as they recommended in their work.

Before loading, the defective graphene is relaxed to the minimum energy configuration using conjugate gradient method. Then, the system is thermally equilibrated by employing a Nosé–Hoover thermostat for 50 ps. After relaxation, uniaxial tension of displacement loading is applied by stretching the cubic box along the x direction. The strain rate of loading is set as 10⁹ s⁻¹, which is commonly used in MD simulations.^33,34 We run all the simulations at the temperatures of 1 K and 300 K, respectively. To avoid thermal noise in the case of 300 K, we present the simulation results of 1 K in this work. The time step is chosen as 1 fs, and the atomic stresses are calculated using Virial theorem.³⁵ The calculations performed with the system are carried out in a parallelized simulation environment, where multiple processors are used to solve the equations of motion. Visualization is carried out by using the Visual Molecular Dynamics (VMD)³⁶ tool.

3. Results and discussions

The tensile stress–strain curves for the defective graphene under various loading directions are shown in Fig. 2a. As the applied strain increases, the stress increases until it reaches the maximum value, which is assumed to be fracture strength σ_f. It can be seen that the resulting tensile strength increases when loading direction transits from armchair direction to zigzag direction. The fracture strength of the defective graphene in zigzag direction (30°) is 110.5 GPa, 20.9% larger than that of graphene in armchair direction (0°).

Fig. 2 Orientational anisotropic effect on the fracture strength of vacancy-defective graphene. (a) Tensile stress–strain curves of the graphene sheet with a vacancy defect in the center subjected to tensile loadings in various directions. The orientation angle θ can be changed from 0° (armchair) to 30° (zigzag) due to the six-fold rotation symmetry of graphene. (b) Relationship between fracture strength of defect-free graphene and the orientation angle θ.

The fracture strength of the defective graphene as a function of the orientation angle θ is plotted in Fig. 2b. For comparison, we also simulated the fracture behavior of defect-free graphene. The dependence of fracture strength of defect-free graphene on the orientation angle θ is given in Fig. 2b. It is observed that both the defect-free and defective graphene exhibit a clear dependence on orientation. For defect-free graphene, Jhon et al.²⁵ proposed a fracture model to predict the relationship between the fracture strength σ_c and the orientation angle θ,

where σ^AC_c is the fracture strength of defect-free graphene with tensile loading in armchair direction, e^AC_c = 0.182 is the corresponding fracture strain of defect-free graphene along the armchair direction. This model can reproduce the MD simulation results, and is able to describe the variation of the fracture strength of defect-free graphene with orientation angle.²⁷ For defective graphene, however, the vacancy defect can cause significant reduce in the fracture strength of graphene.¹⁸ Taken the vacancy defect in graphene as a crack, the fracture strength σ_f of defective graphene with n vacancies can be expressed as,where ρ is the crack tip radius and a is bond length of C–C. With eqn (1) and (2), the dependence of the fracture strength σ_f of defective graphene on the orientation angle θ is derived aswhere the parameter constant C₁ can be calculated based on eqn (1) to be C₁ = 0.716. Since C₂ is not easy to be determined due to the difficulty in estimating the crack tip radius ρ, we fit C₂ with the simulation results in Fig. 2b by eqn (3), and obtain C₂ = 0.785. It is should be noted that for graphene with n-vacancy defect, the parameter C₂(n) is related to two factors, i.e., the vacancy number n and the crack tip radius ρ. According to eqn (2),

For longer crack length n > 1, the crack tip radius ρ(n) is different from ρ(n = 1). So the parameter C₂(n = 1) fitted from simulation result can't be extended to the larger crack (n > 1).

To discuss the effect of vacancy defect on the fracture strength of various orientations, a relative strength is defined as the ratio of the fracture strength of defective graphene and that of defect-free graphene, i.e., η = σ_f/σ_c. In eqn (2), the quantized fracture model does not take the orientational anisotropic effect into account, i.e., the ratio η = σ_f/σ_c in each direction is considered to be a constant C₂. However, we find that this ratio is sensitive and dependent on the orientation angle θ. Fig. 3 shows the variation of η as a function of θ. It can be observed that η in the armchair and zigzag direction are 0.78 and 0.74, respectively. As the uniaxial tensile loading rotates from armchair direction (0°) to zigzag direction (30°), the fracture strength oscillatingly increases to 0.81 at an orientation angle of ∼15°, then they dramatically decrease to 0.74 at the orientation angle of 30°. The defective graphene has the largest ratio η = 0.81 at an orientation angle of ∼15°, indicating that graphene has the least vacancy-defect-induced loss of fracture strength in this direction. On the other side, although the fracture strength in the zigzag direction is larger than that in the armchair direction, the fracture strength in the zigzag direction is more sensitive to the vacancy defect.

Fig. 3 Relative strength ratio η and stress concentration parameter κ as functions of orientation angle θ for graphene with the 1-vacancy defect. There exists an optimal orientation angle θ = 15°, at which the graphene has the minimum stress concentration and largest relative strength.

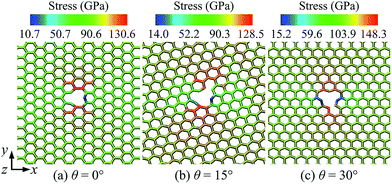
The initial failure states and their corresponding stress distributions for different orientation angles are shown in Fig. 4 to identify the underlying mechanism responsible for the observed behavior. It is obvious that there exists a significant stress concentration around the vacancy defect, which will induce the nucleation of crack. Carbon atoms with the maximum stresses are located in the y direction (perpendicular to the loading direction) around the vacancy defect, while the atoms with minimum stresses are located in the x direction (along the tensile direction). The maximum stresses of the vacancy defective graphene with orientation angles θ = 0°, 15° and 30° are 130.6, 128.5, 148.3 GPa, respectively.

Fig. 4 Initial failure states and their corresponding stress distributions at different orientation angles (a) θ = 0°, (b) θ = 15° and (c) θ = 30°. Carbon atoms in graphene are colored according to the magnitude of their stresses.

In order to describe the stress concentration for different orientations, herein we defined a new parameter κ = σ_t/σ_a, in which σ_t is the average stress for the atoms with the top percentage of stresses (e.g., top 0.1%), σ_a is the average stress of all the atoms. Therefore, a larger κ indicates an uneven distribution of the stress among the atoms while a smaller κ means a more uniform distribution. The relationship between stress concentration parameter κ and orientation angle θ is given in Fig. 3. As the orientation angle increases from 0° to 15°, the stress concentration parameter κ reduces from 1.26 to 1.18, which indicates a relative variation about 6.8%. As the orientation angle θ further increases, the stress concentration parameter κ increases to 1.33, indicating that there is an optimal orientation angle θ = 15° for the defective graphene to have the minimum stress concentration and largest relative strength.

To identify whether the intrinsic material property or the local curvature of the defect causes the orientational anisotropic effect, the fracture strength of a graphene with a larger defect is calculated. As depicted in the inset of Fig. 5, the number of the vacancy is 3 and this 3-vacancy defect is placed in the center of the graphene. Carbon atoms around the 3-vacancy defect are colored in red. The 3-vacancy defect is more closer to the round shape than 1-vacancy defect. The parameter η = σ_f/σ_c of graphene with the 3-vacancy defect as a function of the tensile direction θ is shown in Fig. 5. η can be used to describe the sensibility to defect. It is observed that η for graphene with the 3-vacancy defect is in the range of [0.67, 0.71]. The interval is 0.04, which is much less than that for graphene with the 1-vacancy defect. η for graphene with the 3-vacancy defect shows an weak dependence upon the tensile direction θ, means that the main reason for orientational anisotropic effect is the local curvature of defect. Moreover, the shape and the orientation of the vacancy are relevant. It is should be noted that non-hexagonal carbon rings also exist in graphene. For non-hexagonal carbon rings, the tilting angles and orientation effects of Stone–Thrower–Wales (5-7-7-5) defects on the mechanical properties of graphene have been investigated.³² The fracture strength of STW defective graphene decreases when the tilting angle increases. The shape-orientation coupling for vacancy structures with non-hexagonal carbon rings is complicated, which will be further explored in future work.

Fig. 5 Relative strength ratio η as a function of orientation angle θ for graphene with the 3-vacancy defect. Inset shows the simulation model of 3-vacancy defect.

4. Conclusions

In summary, we have used MD simulations to explore the unique anisotropic vacancy-defect-induced fracture strength loss of graphene. Simulations results showed that the fracture strength in the zigzag direction is more sensitive to the vacancy defect than that in the armchair direction. We also found that the fracture strength of the vacancy-defective graphene has the least sensitivity to the defect at the orientation angle θ = 15°. Our findings are helpful in understanding the orientation-dependent properties of defective graphene and in developing new graphene-based devices for practical applications.

Acknowledgements

This work was supported by China Postdoctoral Science Foundation (Grant no. 2014M562055), the Open Research Fund Program (Grant no. 2042014kf0002) of Wuhan University. C.C. acknowledges the financial support from the Office of Naval Research (Grant N00014-10-1-0907) and NSF's Research Triangle MRSEC (DMR-1121107).

References

1. M. Freitag, Nat. Nanotechnol., 2008, 3, 455.
2. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
3. G. H. Lee, R. C. Cooper, S. J. An, S. Lee, A. van der Zande, N. Petrone, A. G. Hammerberg, C. Lee, B. Crawford and W. Oliver, Science, 2013, 340, 1073.
4. D. Prasai, J. C. Tuberquia, R. R. Harl, G. K. Jennings and K. I. Bolotin, ACS Nano, 2012, 6, 1102.
5. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652.
6. F. Schwierz, Nat. Nanotechnol., 2010, 5, 487.
7. S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282.
8. M. D. Stoller, S. J. Park, Y. W. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498.
9. J. F. Zang, C. Y. Cao, Y. Y. Feng, J. Liu and X. H. Zhao, Sci. Rep., 2014, 4, 6492.
10. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870.
11. K. Brenner and R. Murali, Appl. Phys. Lett., 2011, 98, 113115.
12. C. Ataca, E. Aktürk, H. Şahin and S. Ciraci, J. Appl. Phys., 2011, 109, 013704.
13. Y. M. Chang, H. Kim, J. H. Lee and Y. W. Song, Appl. Phys. Lett., 2010, 97, 211102.
14. S. Badhwar, J. Sibik, P. R. Kidambi, H. E. Beere, J. A. Zeitler, S. Hofmann and D. A. Ritchie, Appl. Phys. Lett., 2013, 103, 121110.
15. A. Zandiatashbar, G. Lee, S. J. An, S. Lee, N. Mathew, M. Terrones, T. Hayashi, C. R. Picu, J. Hone and N. Koratkar, Nat. Commun., 2014, 5, 3186.
16. S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190.
17. H. Bu, Y. Chen, M. Zou, H. Yia, K. Bi and Z. Ni, Phys. Lett. A, 2009, 373, 3359.
18. F. Hao, D. N. Fang and Z. P. Xu, Appl. Phys. Lett., 2011, 99, 041901.
19. S. K. Georgantzinos, G. I. Giannopoulos, D. E. Katsareas, P. A. Kakavas and N. K. Anifantis, Comput. Mater. Sci., 2011, 50, 2057.
20. T. Ma, B. Li and T. Chang, Appl. Phys. Lett., 2011, 99, 201901.
21. K. Min and N. R. Aluru, Appl. Phys. Lett., 2011, 98, 013113.
22. L. Wang and Q. Zhang, Curr. Appl. Phys., 2012, 12, 1173.
23. H. Zhao, K. Min and N. R. Aluru, Nano Lett., 2009, 9, 3012.
24. B. Mortazavi, S. Ahzi, V. Toniazzo and Y. Rémond, Phys. Lett. A, 2012, 376, 1146.
25. Y. I. Jhon, Y. M. Jhon, G. Y. Yeom and M. S. Jhon, Carbon, 2014, 66, 619.
26. C. Carpenter, D. Maroudas and A. Ramasubramaniam, Appl. Phys. Lett., 2013, 103, 013102.
27. M. C. Wang, C. Yan, L. Ma, N. Hu and M. W. Chen, Comput. Mater. Sci., 2012, 54, 236.
28. R. Khare, S. Mielke, J. Paci, S. Zhang, R. Ballarini, G. Schatz and T. Belytschko, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075412.
29. S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472.
30. J. Kotakoski, F. R. Eder and J. C. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201406.
31. X. Li, J. Chen, C. Yu and G. Zhang, Appl. Phys. Lett., 2013, 103, 013111.
32. L. He, S. Guo, J. Lei, Z. Sha and Z. Liu, Carbon, 2014, 75, 124.
33. Y. Dong, Y. He, Y. Wang and H. Li, Carbon, 2014, 68, 742.
34. T. Tang, S. Kim, J. B. Jordon, M. F. Horstemeyer and P. T. Wang, Comp. Mater. Sci., 2011, 50, 2977.
35. A. J. Cao and Y. G. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 214108.
36. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.

---