Mechanical properties and stabilities of g-ZnS monolayers
Abstract
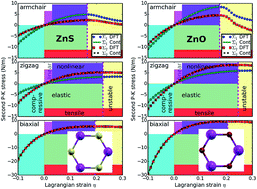
We investigate the mechanical properties and stabilities of the planar graphene-like zinc sulfide (g-ZnS) monolayers under various large strains using electronic structure calculations. The g-ZnS has a low in-plane stiffness, about 1/8 of that of graphene. The potential profiles and the stress–strain curves indicate that the free standing g-ZnS monolayers can sustain large tensile strains, up to 0.16, 0.22, and 0.19 for armchair, zigzag, and biaxial deformations, respectively. However, both the strength and flexibility are reduced compared to graphene-like zinc oxide monolayers. The third, fourth, and fifth order elastic constants are indispensable for accurate modeling of the mechanical properties under strains larger than 0.02, 0.04, and 0.08 respectively. The second order elastic constants, including in-plane stiffness, are predicted to monotonically increase with pressure, while the trend in the Poisson ratio is reversed. Our results imply that g-ZnS monolayers are mechanically stable under various large strains. The elastic limits provide a safe-guide for strain-engineering the g-ZnS based electronics.

 Please wait while we load your content...
Please wait while we load your content...