Structural and magnetic properties of tetragonal perovskite BaFe1−xBixO3−δ†
Abstract
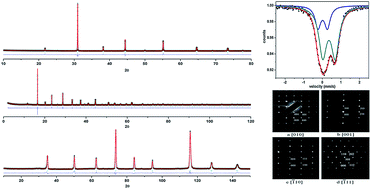
A series of BaFe1−xBixO3−δ (0.09 ≤ x ≤ 0.35) has been synthesized by a traditional solid state method. They all crystallize in space group P4/mmm (with a = 4.0759(1) Å, c = 4.0782(1) Å for x = 0.15) confirmed by the combinational use of powder X-ray, synchrotron, neutron, and electron diffractions. The magnetic susceptibility measurements show that the antiferromagnetic transition for these materials occurs from 64 to 50 K.

 Please wait while we load your content...
Please wait while we load your content...