Effects of strain on the band gap and effective mass in two-dimensional monolayer GaX (X = S, Se, Te)

Abstract

First-principles calculations have been performed to study the mechanical and electronic properties of two-dimensional monolayer GaX (X = S, Se, Te) under strain. It was found that the in-plane stiffness decreases from 86 N m⁻¹ for GaS and 68 N m⁻¹ for GaSe to 57 N m⁻¹ for GaTe, which is in good agreement with experimental results and is attributed to the weakening interactions between Ga and X atoms with the increasing atomic number of the X atoms. The band gaps of the GaX monolayers decrease approximately linearly with increasing tensile strain, while the variation in their band gaps with compressive strain does not show linearity, because the conduction band maximum is transferred among several high symmetry k-points. The effective masses of electrons and holes also exhibit strong anisotropy and can be modulated by applying both compressive and tensile strains, which indicates that monolayer GaX could be very useful for device modeling.

---

1 Introduction

Two-dimensional nanomaterials, such as graphene, transition metal dichalcogenide (TMD) and boron nitride, have been widely studied due to their remarkable physical properties and numerous promising applications.^1–5 Among these, graphene has been the most extensively studied because of its high mobility and rich physics, and because its electronic properties can be controlled by a gate electrode.^2,6,7 Its applications, however, are limited by the absence of a band gap in pristine graphene. In order to become suitable for different applications, the modification of its intrinsic properties is often required. For example, a broad range of chemical decoration^8,9 and substitutional doping^10,11 methods have been investigated to open and tune the band gap of graphene. It has been demonstrated both experimentally and theoretically that the band gap and optical properties of graphene can be controlled and tuned by applying strain.^12,13 Monolayer TMDs, such as molybdenum disulfide (MoS₂), are ideal candidates for using strain engineering as an effective tool to modify their electronic and magnetic properties.^14–17 Additionally, lattice point defects can act as very efficient traps for electrons, holes and excitons, and strongly influence the transport and optical properties of the host materials.¹⁸

Very recently, a stable class of two-dimensional metal dichalcogenide materials, GaX (X = S, Se, Te) monolayers, has been extensively studied for potential applications in photodetectors, gas sensors and optoelectronic devices. Monolayer GaS and GaSe sheets have already been successfully synthesized.^19–22 Compared to graphene, GaX monolayers are intrinsically semiconducting materials with wide band gaps. Each layer of GaX consists of four covalently bonded X–Ga–Ga–X atoms, as illustrated in Fig. 1. Experiments have provided evidence that monolayer GaS and GaSe are perfect candidates for use in field-effect transistors.²¹ Aside from these intriguing features, GaX monolayers show promise for application in nanophotonic devices.¹⁹ Much effort has been devoted to studying the structural, elastic and electronic properties of GaX. Also, the band gap of a GaX monolayer can be widely tuned by mechanical deformation.²³ Accurate hybrid functional and quasiparticle methods predict that GaX structures are suitable photocatalysts for water splitting.²⁴ Although the response of the band gaps of GaS and GaSe to uniaxial and biaxial strain has recently been calculated, other properties, such as their effective masses, have not been considered yet. Additionally, the way in which the band gaps of GaX would behave under compressive strain has not been examined. What is more, the compressive strain can easily be realized in the experiments. These issues actually play an important role in the interpretation of experiments and device modeling. In order to address these issues, a systematic investigation of strain effects on the electronic properties and effective masses of GaX would be highly desirable.

Fig. 1 (a) Side view and (b) top view of monolayer GaX. The green and yellow balls denote Ga and chalcogen atoms, respectively. The rectangular and rhombic regions present the unit cells used to calculate the elastic and electronic properties, respectively. ε_a and ε_z are the strain along the armchair and zigzag directions with respect to the lattice constant, respectively.

In this work, we studied the mechanical and electronic properties of GaX monolayers, but focused on their effective carrier mass and the possible implications of their effective carrier mass. We calculated the elastic parameters of GaX, including in-plane stiffness and Poisson’s ratio. Band gaps of GaX were discussed using both GGA and hybrid functional calculations. The band gaps of GaX could be reduced by both homogeneous tensile (H-strain) and uniaxial tensile strains in either a zigzag (Z-strain) or an armchair (A-strain) direction, while compressive strains tended to have much less influence on the band gap than tensile strains. We also calculated the variation of the effective masses of carriers in GaX with H-strain.

2 Methods

The calculations were performed using the projector augmented wave (PAW) method²⁵ with the generalized gradient approximation of the Perdew–Burke–Ernzerhof (GGA-PBE)²⁶ exchange-correlation functional and the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.²⁷ A (9 × 9 × 1) Monkhorst–Pack²⁸ k-point grid and a plane-wave basis set with an energy cutoff of 500 eV were used for all calculations. A large vacuum layer of more than 12 Å was adopted to prevent interactions between adjacent images. All the structures were fully relaxed with a force tolerance of 0.02 eV Å⁻¹. Numerical calculations were performed using the Vienna ab initio simulation package (VASP).²⁹

3 Results and discussion

3.1 Mechanical properties

We first presented the structural parameters of single-layer GaX (Fig. 1) with PBE functionals, as shown in Table 1. The optimized lattice constants of 3.63 Å for GaS, 3.82 Å for GaSe and 4.13 Å for GaTe using the GGA-PBE functional are consistent with those of previous studies.²⁴ These values are a little larger than the ones (3.59 Å for GaS, 3.75 Å for GaSe) in bulk.^30,31 Because the X and Ga bonds are strongly ionic, the charge transferring from Ga to the X atom can reflect the strength of the X and Ga bonding. Bader charge analysis shows that a little more charge is transferred from Ga to the X atoms in the 3D GaX semiconductors (0.8150 e transferred to each S atom in the GaS monolayer) than in the 2D counterparts (0.8104 e transferred to each S atom in bulk GaS). Stronger bonding between the Ga and X atoms in bulk GaX leads to shorter Ga–X bonds and smaller lattice constants.

Table 1 The structural parameters and elastic parameters of single-layer GaX on the GGA-PBE level. d₁ and d₂ are the distances between two Ga atoms and two X (X = S, Se, Te) atoms, respectively. t₁ and t₂ are the fitting parameters. ν and C represent Poisson’s ratio and in-plane stiffness, respectively

	d1 (Å)	d2 (Å)	a0 (Å)	t1	t2	ν	C (N m^−1)
GaS	4.63	2.47	3.63	32.75	12.67	0.244	85.87
GaSe	4.82	2.47	3.82	28.15	12.53	0.248	67.14
GaTe	5.02	2.47	4.13	26.16	12.9	0.246	56.46

---

Next, we discussed the strain energy before analyzing the elastic properties of GaX. Strain energy gives an insight into the influence of strain on the structural and elastic properties and it can be illustrated as E_S = E_T(ε) − E_T(ε = 0), where E_T(ε) is the total energy at a given axial strain ε, and E_T(ε = 0) is the total energy at equilibrium state. The evolution curves of strain energy of GaS, GaSe and GaTe with the three types of strain illustrated above are shown in Fig. 2. For both tensile and compressive strains within the loaded range, the strain energy increases monotonically with the corresponding increasing strain. The harmonic approximation is well applied with −0.02 < ε < 0.02, beyond which the E_S – ε curve becomes inharmonic because the contributions of higher order terms are larger than 10% and noticeable.

Fig. 2 The evolution of the strain energy E_S of (a) GaS, (b) GaSe and (c) GaTe with strain.

All the curves show their minima at zero strain. It is clear that the A-strain and Z-strain exert almost the same influence on the strain energy of GaX. This can be attributed to the hexagonal lattices with honeycomb structures of the GaX monolayers. Their mechanical properties, including in-plane stiffness, are isotropic even under small strains, which results in the equal contribution of intralayer interactions between Ga and X atoms along both the A-direction and Z-direction. From the atomic configuration of GaX in Fig. 1, we can see that the intralayer interaction mainly comes from the Ga–X bonding. The three Ga–X bonds for each X atom result in the equal contribution along the A-direction and Z-direction.

We then discussed the elastic properties of GaX, which are usually characterized by two independent constants: Young’s modulus Y and Poisson’s ratio ν. However, it is difficult to calculate the thickness of the sheet system, which is required in calculating Young’s modulus. Calculating the in-plane stiffness is an alternative way with respect to Young’s modulus. The in-plane stiffness C can be defined as C = (1/S₀)(∂²E/∂ε²), where S₀ is the equilibrium area, E is the total energy, and ε is uniaxial strain (ε = Δa/a). The other parameter, Poisson’s ratio ν, is the ratio of transverse strain to axial strain, namely, v = −ε_strans/ε_axial. To calculate the elastic properties of GaX, we constructed a rectangular unit cell of GaX, which contains two GaX molecules, as seen in Fig. 1.^32–34 In our calculations, the two lattice constants, a_z and a_a, are changed from −2% to 2% in increments of 1%. The system is fully re-optimized and the corresponding total energy is obtained at each (ε_a, ε_z) point. Afterwards, the total energy can be written as E = t₁ε_z² + t₁ε_a² + t₂ε_zε_a + E₀, in which E₀ is the total energy at equilibrium state; ε_z and ε_a are the strains along the zigzag and armchair directions, respectively; and t₁ and t₂ are related coefficients. The in-plane stiffness and Poisson’s ratio finally can be calculated using C = (1/S₀)(2t₁ − t₂²/2t₁) and v = t₂/t₁.

Table 1 gives the fitting parameters t₁ and t₂ as well as elastic constants C and ν. These elastic parameters were determined by using the method based on strain energy calculation in the harmonic elastic deformation range. The in-plane stiffness C values of GaS, GaSe and GaTe are 86, 68 and 57 N m⁻¹, respectively. Also, their Poisson’s ratios are 0.244, 0.248 and 0.246. The calculated results of in-plane stiffness C are in good agreement with the reported results of 98 N m⁻¹ for GaS, 79 N m⁻¹ for GaSe and 66 N m⁻¹ for GaTe.²⁴ It is clear that the in-plane stiffness is decreased with the increasing atomic number of the chalcogen atoms, whereas the Poisson’s ratio varies by a small amount among them. From the formula of in-plane stiffness, we can see that the C is dominated by t₁ when t₁ is larger than t₂. t₁, to some extent, reflects the strength of the intralayer interactions of the GaX monolayer. With the increasing atomic number of the chalcogen atoms, the bonding between the Ga atoms and chalcogen atoms becomes weaker, leading to a smaller t₁ and relatively smaller in-plane stiffness.

In order to gain a further insight, the binding energies of the chalcogenide atoms in the GaX monolayer were calculated and are presented in Table 2. We constructed a supercell containing 4 × 4 × 1 unit cells in the binding energy calculations. The binding energy was defined as the difference between the total energy of a GaX supercell and the sum of the total energy of a GaX supercell with a vacancy at the chalcogenide atom site and that of an isolated chalcogenide atom:

E_b = E_supercell − E_withvacancy − E_chalcogenide

where E_supercell and E_withvacancy are the total energies per unit cell of the supercell without and with a vacancy at chalcogenide atom site, respectively, and E_chalcogenide is the energy of an isolated chalcogenide atom. Consistent with the above analysis, as the atomic number of the chalcogenide increases, its binding energy in the corresponding GaX monolayer decreases numerically, which implies the weakening of the bonding between X atoms and Ga atoms with X changing from S to Te. Furthermore, as the Ga–Ga bonds are perpendicular to the plane of the GaX monolayers, the bonds between the Ga atoms and X atoms make the main contribution to the in-plane stiffness. It can be concluded that stronger binding between the Ga atoms and chalcogen atoms results in a larger in-plane stiffness.

Table 2 The binding energy (E_b) values of chalcogenide atoms in GaX monolayers on the GGA-PBE level and the band gaps of these monolayers on both the GGA-PBE and HSE06 levels are listed here. The average charge values of every atom of GaX in the equilibrium state are given too

	Eb (eV)	Charge of X	Charge of Ga	Band gap (PBE, eV)	Band gap (HSE06, eV)
GaS	−6.963	6.8104	12.1896	2.48	3.19
GaSe	−6.354	6.6615	12.3385	1.83	2.71
GaTe	−5.709	6.4438	12.5562	1.44	2.02

---

3.2 Electronic properties

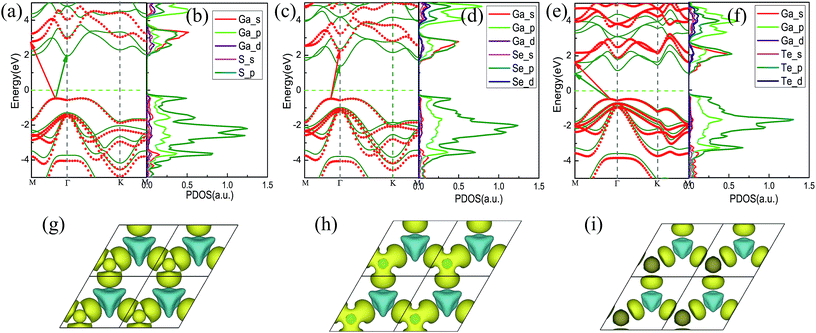
We then studied the band structures of the unstrained GaX monolayers using both PBE and HSE06 calculations. As shown in Fig. 3(a), (c) and (e), all three monolayers are indirect-band gap semiconductors. Their band gaps, calculated on the PBE and HSE06 levels, are listed in Table 2. The general features of the band structures calculated using PBE and HSE06 are similar, except that the band gap calculated using HSE06 is much larger than the other, because PBE usually underestimates band gaps. Our results are in great agreement with previous results.^23,24

Fig. 3 Band structures and the projected density of states of monolayer GaX without strain are shown in (a)–(e). The solid lines and filled circles in the band structures represent the results calculated using GGA-PBE and HSE06, respectively. The solid arrows indicate the lowest energy transition. (g)–(i) show the charge redistribution diagrams of GaS, GaSe and GaTe, respectively.

In order to determine the constituents of the electronic bands, the projected densities of states (PDOSs) were also calculated using the PBE functional and are shown in Fig. 3(b), (d) and (f). Each of them shows a gap near the Fermi level, which is smaller than the corresponding calculated value of the band structure due to the shift of the conduction band minimum (CBM) and the valence band maximum (VBM) towards the Fermi level. For the unstrained GaS, the CBM and the VBM are mainly constituted by S – p states and Ga – p states.

From Fig. 3 and Table 2, it can be seen that the band gap of the unstrained GaX monolayer decreases as we go down the column of X atoms in the periodic table. This is possibly caused by the increasing delocalization of the atomic orbitals, which leads to reduced interactions between the Ga and X atoms and an increased lattice constant. These conclusions are further supported by the redistribution of charges, which is calculated by taking the difference of the total charge of GaX and the sum of the charges of isolated chalcogenide and Ga atoms, as shown in Fig. 3(g)–(i). In the GaX monolayers, the Ga–X bond is strongly ionized and the delocalization could reflect the strength of the atomic interaction, similar to the TMDs.^35–37 In this work, the GaS monolayer shows the maximum redistribution of the charge of the three GaX monolayers. The increased charge transfer from the Ga atom to the chalcogen atom and the smaller lattice constant of GaS lead to stronger interactions between the Ga and S atoms.

We then studied the behavior of the band gap of GaX under strain by using GGA-PBE. We considered three types of strain: uniform biaxial strain (H-strain), uniaxial strain along the armchair direction (A-strain) or zigzag direction (Z-strain). Fig. 4 presents the Brillouin zone (BZ) of GaX monolayers under strain. The irreducible BZ of GaX remains unchanged under H-strain, as the hexagonal symmetry is preserved. In Fig. 4(a), the R point and S point are equivalent to the K point and M point, respectively. In the cases of A-strain and Z-strain, the structure of the BZ is deformed as the hexagonal symmetry is degenerated to rhombic symmetry, and the irreducible BZ becomes a right trapezoid from the original triangular shape. Moreover, the high-symmetry k-points increase from three (Γ, K, M) to five (Γ, K, M, R, S).

Fig. 4 Brillouin zone with high-symmetry points of monolayer GaX under (a) H-strain, (b) A-strain and (c) Z-strain.

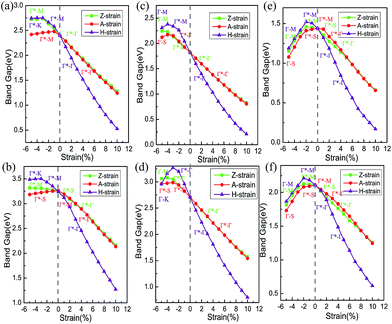
We constrained the tensile strain within the range of 0 to 10% in our calculations and a small compressive strain ranging from −5 to 0% was imposed. The variation of the band gaps of GaX calculated using GGA-PBE as a function of strain is summarized in Fig. 5. Γ* denotes the maximum points of the valence band located at the side of the Γ point and the label of k–k* along each curve denotes that the VBM and CBM are located at the k point and k* point, respectively, under the corresponding strain. In the case of tensile strain, the band gaps of GaX decrease approximately linearly. While the variation of band gaps with compressive strain does not show linearity because the conduction band maximum is transferred among several high symmetry k-points. Take GaS under H-strain as an example, the variation of its band gap calculated by PBE is plotted with a violet line in panel (a) of Fig. 5. The CBM and VBM are marked along the curve. Under tensile strain, the curve is labelled with Γ*–Γ, which means the VBM is located at the Γ* point and the CBM is located at the Γ point. When under compressive strain, the VBM remains at the Γ* point. The CBM, however, is transferred from the Γ point to the M point, then to the K point. On the other hand, A-strain and Z-strain exert a similar influence on the band gap of GaX. All the results show that the band gaps of GaX can be modified over a wide range by applying tensile strain.

Fig. 5 (a), (c) and (e) show the GGA-PBE results of the variation in the band gaps of GaS, GaSe and GaTe versus strains, respectively. The panels below these correspond to the HSE06 results. Γ* denotes the maximum points of the valence band, which is located at the side of the Γ point, and the label of k–k* along each curve denotes that the VBM and CBM are located at the k point and k* point, respectively, under the corresponding strain.

We checked the variation of the band gaps of GaX with applied strains by calculating the band structures using the HSE06 functional method, which is also shown in Fig. 5. Although the calculated HSE06 band gaps of GaX are larger than the PBE ones, the nature of the band structure remained unchanged.

The decreasing band gap of GaX with increasing tensile strain implies a reduced interaction between Ga and X atoms, which could be caused by the increasing distance between them. Due to the increase in the chalcogen atomic radius, the bond length between Ga and X atoms also increases in the sequence of GaS < GaSe < GaTe, which results in the weakening of the bonding between Ga and X. This can be clearly seen from the binding energies listed in Table 2. Our PBE calculations show that the binding energies are −6.963 eV for GaS, −6.354 eV for GaSe and −5.709 eV for GaTe. Using Bader charge analysis,^38–40 we obtained the values for the charge transfer from Ga to the chalcogen atoms (Fig. 6). Each Ga atom loses 0.81 e in the GaS sheet, 0.66 e in the GaSe sheet and 0.44 e in the GaTe monolayer. Due to the small charge transfers and increased lattice constants, the binding energies of the GaS, GaSe and GaTe monolayers decrease. This, essentially, results in weaker interactions between the M and X atoms and a decreasing band gap from GaS to GaTe, which is in good agreement with our above interpretation.

Fig. 6 Average Bader charges of Ga and X atoms for GaX monolayers as a function of strain. For the respective GaX monolayers, the charges of the Ga and X atoms are plotted in the same color.

Strain also has an effect on the curvature of the band structure, reflected in a change in the effective masses of electrons and holes. The effects of strain on the effective masses of the electrons and holes of GaX under H-strain are reported in Fig. 7. The effective mass is calculated using m = ħ²/(∂²E/∂k²), and the k points closely approach the corresponding k-point, such as VBM and CBM. In Fig. 7, Γ_R and Γ_L denote the Γ* points to the right (in the K point direction) and left (in the M point direction) of the Γ point, respectively. The variation curve of the effective mass of an electron (or hole) at k-point in the k*-point direction is labeled by k–k*. For example, the curve labeled Γ–M shows the evolution of the effective mass of electrons at the Γ point in the M point direction. For simplification, only the effect of H-strain on effective masses was taken into consideration in this work. The R point and S point, as a result, are equivalent to the K point and M point, respectively.

Fig. 7 The variation of effective masses (in units of electron mass m₀) of (a) electrons and (b) holes at high symmetry points of GaS with H-strain. (c and d) and (e and f) are the corresponding contents of GaSe and GaTe, respectively. Γ_R and Γ_L denote the Γ* points to the right (in the K point direction) and left (in the M point direction) of the Γ point, respectively. The masses are labeled by the band extremum and the direction along which the mass is calculated.

Because the effective mass of electrons (holes) is determined by the dispersion of energy at the CBM (VBM), the jumping of CBM (VBM) will lead to a dramatic change in the associated effective mass value. Take GaS as an example, when a compressive strain is imposed, the CBM shifts from the Γ point to the M point and then to the K point. The mass of the electron at the M point in the K direction is smaller than at the K point and is larger than at Γ. The jumping of the CBM, essentially, results in a dramatic change in the effective mass of the electron. For holes, the relevant VBM is near the Γ point, without jumping to other points with strain. The masses of the holes at the Γ_L point and Γ_R point show similar variation in trend and degrade slowly with increasing strain. This suggests that the effective mass of the holes of GaS will not change dramatically.

When under a tensile strain of more than 2%, it is worth noting that the VBM and CBM are located at the Γ* and Γ points, respectively, and remain unchanged with increasing tensile strain. The effective mass of electrons for the band extremum at Γ is not very sensitive to strain, while the effective mass of holes decreases slowly with the tensile strain, implying the maintenance of the quality of the conductivity. The modification of the band gap without significant alteration of the dispersion of the bands is very important for electronic applications. Furthermore, the mass of electrons is much smaller than that of holes regardless of the applied stain, implying that the GaX will have important applications as an n-type material in field effect transistors. What’s more, the effective mass of electrons in stretched GaX increases from GaS to GaTe, which suggests that GaS may show better transport properties than GaSe and GaTe.

4 Conclusions

In summary, first-principles calculations were carried out to reveal the elastic and electronic properties of GaX (X = S, Se, Te) under strain. GaS, GaSe and GaTe show similar elastic, electronic and transport properties, because they share the same atomic configuration and spatial symmetry group. The in-plane stiffness was found to decrease gradually with the increasing atomic number of the chalcogen atoms, whereas the Poisson’s ratio values varied by a small amount among them. Upon the application of strain, the band gaps of GaX could be modified and tuned over a relatively large range. In the case of tensile strain, the band gaps of GaX decreased approximately linearly, while the variation of the band gaps with compressive strain did not show linearity, because the conduction band maximum is transferred among several high symmetry k-points. Besides, the A-strain and Z-strain exert a similar effect on the band gap of GaX. The effects of strain on the effective masses of electrons and holes are reported in Fig. 7. The jumping of the CBM leads to dramatic changes in the associated effective mass value. Additionally, the plots of the effective carrier mass also provide a meaningful insight into the transport performance of strained monolayer GaX structures. In practice, these strains could potentially be realized by epitaxial growth on suitable substrates. Our results will be useful for interpreting the variable mobilities and transport properties of strained GaX electronic devices in experiments. Besides, the band gap of GaX can be modified by tensile strain without a significant change in the dispersion of the bands, which is very important for electronic applications.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant no. 91233120 and the National Basic Research Program of China (2011CB921901).

References

1. K. Novoselov, D. Jiang, F. Schedin, T. Booth, V. Khotkevich, S. Morozov and A. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
2. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
3. A. C. Neto, F. Guinea, N. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
4. C. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 195505.
5. H. L. Zhuang and R. G. Hennig, J. Phys. Chem. C, 2013, 117, 20440–20445.
6. K. Novoselov, A. K. Geim, S. Morozov, D. Jiang, M. Katsnelson, I. Grigorieva, S. Dubonos and A. Firsov, Nature, 2005, 438, 197–200.
7. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204.
8. D. Elias, R. Nair, T. Mohiuddin, S. Morozov, P. Blake, M. Halsall, A. Ferrari, D. Boukhvalov, M. Katsnelson and A. Geim, et al., Science, 2009, 323, 610–613.
9. H. Şahin and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035452.
10. Z.-H. Sheng, H.-L. Gao, W.-J. Bao, F.-B. Wang and X.-H. Xia, J. Mater. Chem., 2012, 22, 390–395.
11. Y. Wang, Y. Shao, D. W. Matson, J. Li and Y. Lin, ACS Nano, 2010, 4, 1790–1798.
12. G. Cocco, E. Cadelano and L. Colombo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 241412.
13. G. Gui, J. Li and J. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075435.
14. E. Scalise, M. Houssa, G. Pourtois, V. Afanasev and A. Stesmans, Nano Res., 2012, 5, 43–48.
15. W. S. Yun, S. Han, S. C. Hong, I. G. Kim and J. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 033305.
16. H. Peelaers and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 241401.
17. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695–1701.
18. S. Tongay, J. Suh, C. Ataca, W. Fan, A. Luce, J. S. Kang, J. Liu, C. Ko, R. Raghunathanan and J. Zhou, et al., Sci. Rep., 2013, 3, 2657.
19. P. Hu, L. Wang, M. Yoon, J. Zhang, W. Feng, X. Wang, Z. Wen, J. C. Idrobo, Y. Miyamoto and D. B. Geohegan, et al., Nano Lett., 2013, 13, 1649–1654.
20. D. J. Late, B. Liu, H. Matte, C. Rao and V. P. Dravid, Adv. Funct. Mater., 2012, 22, 1894–1905.
21. D. J. Late, B. Liu, J. Luo, A. Yan, H. Matte, M. Grayson, C. Rao and V. P. Dravid, Adv. Mater., 2012, 24, 3549–3554.
22. S. Lei, L. Ge, Z. Liu, S. Najmaei, G. Shi, G. You, J. Lou, R. Vajtai and P. M. Ajayan, Nano Lett., 2013, 13, 2777–2781.
23. Y. Ma, Y. Dai, M. Guo, L. Yu and B. Huang, Phys. Chem. Chem. Phys., 2013, 15, 7098–7105.
24. H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238.
25. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 9906.
28. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
29. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11–169.
30. A. Kuhn, A. Chevy and R. Chevalier, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 983.
31. A. Kuhn, A. Chevy and R. Chevalier, Phys. Status Solidi A, 1975, 31, 469–475.
32. M. Topsakal, S. Cahangirov and S. Ciraci, Appl. Phys. Lett., 2010, 96, 091912.
33. Q. Yue, S. Chang, J. Kang, S. Qin and J. Li, J. Phys. Chem. C, 2013, 117, 14804–14811.
34. J. Kang, J. Li, F. Wu, S.-S. Li and J.-B. Xia, J. Phys. Chem. C, 2011, 115, 20466–20470.
35. Y. Ding, Y. Wang, J. Ni, L. Shi, S. Shi and W. Tang, Phys. B, 2011, 406, 2254–2260.
36. J. Kang, S. Tongay, J. Zhou, J. Li and J. Wu, Appl. Phys. Lett., 2013, 102, 012111.
37. S. Bhattacharyya and A. K. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075454.
38. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
39. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
40. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.

---