New insights into the relationship between structure and photocatalytic properties of TiO₂ catalysts

Abstract

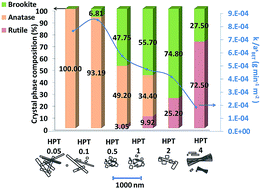
This work systematically investigated the relationship between structure, morphology, photoelectrochemical (PEC) and photocatalytic (PC) properties of TiO₂ catalysts. A series of TiO₂ catalysts with various phase compositions (anatase-, brookite- and finally rutile-rich samples) and morphologies (1D morphology, rhomboid nanoparticles (NPs) and flower-like assemblies of nanorods) were prepared by an acidic hydrothermal treatment of hydrogen titanate nanofibres (H-TNFs). The structures of the samples, such as crystal phase composition and their spatial distribution, were extensively characterised, and the samples were tested for photocatalytic degradation of ethanol. A strong correlation is found between PEC and PC properties. PEC measurements revealed that the brookite-rich samples generated high but unstable photocurrents. The anatase and rutile-rich samples showed good stability, but for the rutile-rich samples low photocurrents were detected due to the poor conductivity of this polymorph. In contrast, the sample containing 93.2% anatase and 6.8% brookite with elongated morphology not only showed the ability to generate high photocurrents but also maintained a stable photoresponse upon an extended period of time, because of its well-balanced bi-crystalline structure and elongated morphology. Therefore, the abilities to generate high photocurrents and to maintain a stable photoresponse are equally important and probably a prerequisite for a good photocatalyst.

---

1. Introduction

Because of the increasing pollution of water resources and air, there is a growing interest to find cheap and sustainable solutions to purify these media. TiO₂ has been widely investigated in the last several decades as a photocatalyst and may offer promising solutions to decompose harmful organic contaminants in air and in water. However, to efficiently apply TiO₂ in practice as an air and water cleaning agent, two main drawbacks should be overcome. One is its wide band gap (E_g of anatase = 3.2 eV; E_g of rutile = 3.0 eV), which limits the utilisable light in the wavelength range to ≤390 nm to trigger the essential electron–hole separation, which is the initial step of the photocatalytic process; the other is its low quantum efficiency owing to the fast recombination of the generated electrons and holes which normally happens in the time domain of 10⁻¹¹ to 10⁻⁶ s,¹ limiting the diffusion of many charge carriers from the bulk to the surface of the particles.

The photocatalytic behaviour of TiO₂ is closely related to its structure and phase composition. TiO₂ is known to have several crystal phases among which the most common are the thermodynamically stable rutile (tetragonal, P4₂/mnm) and the meta-stable phases of anatase (tetragonal, I4₁/amd) and brookite (orthorhombic, Pbca). Anatase has been widely reported as the most active crystal phase.^2–5 It might be due to it comparatively long life-time of generated electron–hole pairs in the bulk which was proven by transient photoconductivity measurements.⁶ Another explanation is that, although it has a wider band gap than rutile that will narrow the wavelength range of the incoming light, its conduction band minimum is more likely to lie above the reduction potential of the adsorbate, and the valance band maximum below the oxidation potential of the adsorbate, which are necessary conditions for the occurrence of electron and hole transfer in a photocatalytic reaction.⁷ Also, it is reported that polycrystalline TiO₂ has better activity than the single crystalline counterparts due to the suppressed electron–hole recombination as a result of the rapid transport of electrons between different crystal phases.^8,9 In addition, surface area, pore volume, pore size and crystallinity,¹⁰ defect sites,¹¹ exposed facets^12–14 as well as the particle morphology are reported as the physical parameters that can influence the activity. The particle morphology not only relates to the exposed facets, but also impacts the electron transport mechanisms within the structure. It has been reported that the number of generated charge carriers is higher on elongated nanostructures, as this morphological feature gives rise to fast transport of electrons along the 1D morphology hindering the recombination of charge carriers.^15,16 Therefore 1D and self-branching titania nanostructures are gaining more prominence to be used in photoelectrochemical devices as it has been shown by latest reports.^17–19 Although extensive efforts have been made to elucidate the structure–photocatalytic property relationship for the TiO₂ catalysts, there is still no final conclusion that has been reached on this issue.

Since the crystal phase composition and structure play important roles in determining the catalytic performance, it is extremely important to have a good control on these properties in catalyst preparation. Zhu et al. first demonstrated that hydrothermal treatment of hydrogen titanates with dilute nitric acid solution could topochemically convert hydrogen titanate nanofibres (H-TNFs) into anatase nanocrystals, and observed an enhanced photocatalytic decomposition of synthetic dye sulforodamine on the catalysts.²⁰ This method provides not only a practical approach to the synthesis of TiO₂ catalysts in aqueous solution under relatively mild conditions, also a good control over the physical and chemical properties of the resulted material by changing the reaction conditions such as reaction time, temperature or pH using a variety of acids.^20–23 Moreover, compared to the conventional heat treatment method, the hydrothermal treatment often yields TiO₂ with higher surface area,²⁴ relatively higher degree of crystallinity and better control over the particle size.²⁵

In this study, we prepared a series of TiO₂ samples by the hydrothermal treatment of H-TNFs. By adjusting the acid concentration of the reaction medium, we systematically tuned the crystal phase composition of TiO₂ and investigated how the structural and morphological characteristics affected the electronic features and the photocatalytic properties. It is found that the abilities to generate enhanced photocurrents and maintain a stable photoresponse are equally important and probably are prerequisites of a good TiO₂ photocatalyst.

2. Experimental

2.1. Synthesis of materials

Typically, Na-TNFs were synthesised by dispersing 3.84 g TiO₂ nanopowder (P25 grade, Aeroxide) in 80 mL 10 M aqueous solution of NaOH (reagent grade pellets, Sigma-Aldrich) in a Teflon-lined autoclave, then the mixture was hydrothermally treated at 180 °C for 48 h. The as-synthesised Na-TNFs product was washed with 2 L ultrapure water then re-dispersed and stirred in 1 L of 0.5 M HCl (reagent grade, Sigma-Aldrich, 37 wt%) overnight (∼50–55 mmol HCl per g solid) to obtain H-TNFs by ion exchange. The sample was washed again with ca. 1.5 L ultrapure water until pH ∼ 5 then dried in an oven at 60 °C. Various titania nanostructures were prepared by the acidic hydrothermal treatment as follows: 1.0 g of the as-prepared H-TNFs was hydrothermally treated at 120 °C for 24 h in 80 mL 0.05–4 M HNO₃ solutions to obtain samples denoted as HPT0.05; HPT0.1; HPT0.5; HPT1; HPT2 and HPT4, respectively, in which HPT stands for hydrothermal post treatment and the number indicates the acid concentration of reaction medium in mol (M). The samples were washed with ca. 1.0 L ultrapure water until pH ∼ 5 then dried in an oven at 60 °C and were annealed at 300 °C for 1 h in air (with a heat up rate of 5 °C min⁻¹). Finally, the samples were ground in a mortar and kept in closed glass vessels until use.

2.2. Characterisation

The powder X-ray diffraction (PXRD) data of the samples were measured in Bragg–Brentano geometry using a Bruker D8 diffractometer (Bruker-AXS GmbH, Karlsruhe, Germany) equipped with a Cu-Kα source, 2.5 degree soller slits, 0.5 degrees divergence slit, an air scattering screen and a gas-filled position sensitive detector. Rietveld refinements were performed with Topas v4.2 (Bruker-AXS-GmbH, Karlsruhe, Germany) using the fundamental parameter approach.²⁶ The background was fitted with a Chebychev polynomial of order 15. Zero-shift, lattice parameters, an overall isothermal displacement parameter, scale factors and Lorentz crystallite size broadening were refined. The composition of the crystalline components was obtained from the Rietveld scale factors of the crystalline phases using the method developed by Howard and Hill.²⁷ The crystallite size was determined based on the volume weighted integral peak width according to the fundamental parameter approach²⁶ as implemented in Topas. This means that a value averaged over all diffraction peaks (crystal directions) is obtained. This type of analysis assumes that all crystallites are spherical which is, of course, unrealistic and can lead to some discrepancy between the XRD and the TEM results. Transmission electron microscopy (TEM) measurements were conducted on a TECNAI TF20 SuperTwin (200 kV) microscope. The Raman spectra were recorded on a Renishaw InVia Raman microscope (Renishaw plc, New Mills, UK) using a near-IR laser (785 nm) and a ×50 objective. The analysis of signals and deconvolution of spectra were performed with an in-house developed algorithm Band-Target Entropy Minimization (BTEM®), using MATLAB® 7.12.0 R2011a (The MathWorks, Natick, MA, USA). Numerical calculations were performed on an Intel Pentium CPU G640 2.80 GHz processor with 4 GB of RAM. N₂ sorption measurements were carried out at 77 K using a Micromeritics ASAP2420 type instrument. Prior to the measurements, the samples were degassed at 200 °C for 24 h. UV/VIS spectra were recorded on a UV-3600 UV-VIS-NIR spectrophotometer (Shimadzu, Japan). BaSO₄ was used to prepare pellets of the solid samples. All electrochemical measurements were performed on an Autolab PGSTAT302 instrument in a classical one-compartment and three-electrode electrochemical cell. TiO₂ NPs were coated on ITO glass electrodes (0.16 mg cm⁻²) via spray coating and used as the working electrode. A large Pt foil counter-electrode and an Ag/AgCl/3 M KCl reference electrode completed the cell setup. The light source was a 300 W Hg–Xe arc lamp (Hamamatsu L8251). The radiation source was placed 2 cm away from the working electrode surface. Photovoltammetry profiles were recorded in both 0.1 M Na₂SO₃ and 0.1 M Na₂SO₄ electrolyte, using a slow potential sweep (2 mV s⁻¹) in conjunction with interrupted irradiation (0.1 Hz) on the semiconductor coated electrodes. All above procedures were performed at the laboratory ambient temperature (20 ± 2 °C).

Photocatalytic degradation of ethanol vapour on the photocatalysts was conducted in a flat film reactor (V = 0.165 L) at room temperature (25 ± 0.1 °C). The light source was a low-pressure mercury lamp (GCL303T5/4 type, LightTech, Hungary) mostly emitting light above 360 nm. The concentration of ethanol vapour was monitored by a Shimadzu GC-14B type gas chromatograph equipped with a thermal conductive detector (TCD) and with a flame ionization detector (FID). The initial amount of ethanol in the reactor was 2.76 mg (c = 0.36 mM).

3. Results and discussion

3.1. Phase composition, morphology and textural properties

The sodium titanate nanofibres (Na-TNFs), obtained from the high alkali hydrothermal treatment of P25 TiO₂, are well crystallised and identified as Na₂Ti_nO_2n+1 (n = 3, 4, 9) according to the reference data (JCPDS 31-1329, 33-1294 and 33-1293, respectively). The solid was thoroughly washed with DI water to remove the excess amount of NaOH then stirred in dilute HCl solution to exchange intercalated Na⁺ with H⁺ ions. This step initiated the conversion of Na₂Ti_nO_2n+1 (n = 3, 4, 9) into hydrogen titanates (H-TNFs). After washing with water and drying, H-TNFs were crystallised as a mixture of hydrogen titanium oxide (H₂Ti₂O₇, JCPDS 00-047-0561) and hydrogen titanium oxide hydrate (H₂Ti₅O₁₁3H₂O, JCPDS 00-044-0130). These results show good agreement with previous work of another group.²⁸ The XRD patterns of the as-prepared Na-TNFs and H-TNFs are shown in ESI Fig. 1.† H-TNFs were further exposed to the acidic hydrothermal post-treatment (HPT) at 120 °C for 24 h in 0.05–4 M HNO₃ to obtain TiO₂ with various crystal phase compositions and morphologies. The XRD patterns of these products are shown in Fig. 1. Reflections at 2θ = 25.28°, 37.80°, 48.05°, 53.89° and 55.06° were observed in HPT0.05, HPT0.1, HPT0.5 and HPT1 and assigned to (101), (004), (200), (105) and (211) planes of anatase, respectively. The samples of HPT0.1, HPT0.5, HPT1, HPT2 and HPT4 showed reflections indicative of brookite at 25.36°, 25.71°, 30.83° and 36.28°, 48.06° and 55.28°, which were referred to (210), (111), (211), (102), (321) and (421) planes, respectively. Rutile phase was identified in samples from HPT0.5 to HPT4 from reflections at 2θ = 27.24°, 35.81°, 40.93°, 53.90°, 56.20° and 68.45°, which were referred to (110), (101), (111), (211), (220) and (301) planes of rutile, respectively. By visually comparing the PXRD patterns in Fig. 1, it can readily recognise that anatase-, brookite, and finally rutile-rich samples have been obtained by decreasing the pH of the reaction medium.

Fig. 1 XRD patterns of HPT TiO₂ samples: ◊ anatase; ○ brookite; ● rutile.

Quantitative comparison of the crystalline phase composition of the samples was assessed from the XRD patterns using Rietveld refinement (ESI Fig. 2†). It is worth noting that there was a small amount of amorphous TiO₂ present in all samples which was not quantitatively determined. The composition of crystalline phases of the samples are summarised in Table 1. Anatase was present in samples HPT0.05–HPT1. While HPT0.05 contained solely anatase in the crystalline phase, a low amount of brookite (6.8%) was formed in HPT0.1 besides the dominant anatase phase. Further increasing the acid concentration, the amount of brookite phase became more significant and reached its highest proportion (74.8%) in sample HPT2. After this point (≥2 M HNO₃), the formation of brookite was hindered due to the progressive evolution of rutile. This latter phase was first detected in sample HPT0.5 in a small quantity (3.05%). The volume-weighted domain size of the anatase, brookite and rutile crystallite sizes were determined from XRD patterns based on Lorentz crystallite size-broadening, as shown in Table 1. The anatase crystallites were observed to be relatively small (9.5–7.9 nm) in samples HPT0.05 to HPT1 and the average dimension slightly decreased with the progressive evolution of brookite at lower pH values. It was a competitive process between the different crystal phases: the size of anatase crystallites was gradually decreased as the proportion of brookite was increased. The brookite phase appeared first in HPT0.1 with an average crystallite size of 37.0 nm. This value was determined to be larger at higher acidic conditions for samples HPT0.5 and HPT1 (53.1 and 50.3 nm, respectively). After this significant increase in crystallite size, the growth was suppressed with the gradual increase of rutile, which first appeared in HPT1. The average crystallite size for rutile was first measured to be 47.0 nm for HPT0.5. When the pH was further decreased, the crystal size for rutile first increased to 63.4 nm (HPT1), and then gradually decreased to 24.0 nm (HPT4).

Table 1 Crystal phase composition of HPT TiO₂ samples obtained from XRD measurements by Rietveld refinement and volume weighted integral crystallite sizes were calculated from Lorentz crystallite size broadening

Sample ID	Crystal phase composition (%)			Crystallite size (nm)
	Anatase	Brookite	Rutile	Anatase	Brookite	Rutile
HPT0.05	100	—	—	9.5 ± 2.0	—	—
HPT0.1	93.2 ± 1.2	6.8 ± 1.2	0	9.2 ± 3.1	37.0 ± 11	—
HPT0.5	49.2 ± 2.9	47.7 ± 2.9	3.05 ± 2.9	8.0 ± 3.9	53.1 ± 3.7	47.0 ± 1.4
HPT1	34.4 ± 2.6	55.7 ± 2.7	9.9 ± 1.0	7.9 ± 5.4	50.3 ± 2.8	63.4 ± 7.3
HPT2	—	74.8 ± 1.1	25.2 ± 1.1	—	33.9 ± 0.5	49.7 ± 1.4
HPT4	—	27.5 ± 1.5	72.5 ± 1.5	—	15.9 ± 0.5	24.0 ± 0.3

---

The structural differences essentially led to the formation of various morphologies of TiO₂ such as fibres, rhomboid NPs and flower-like aggregates (Fig. 2A–I). Under the relatively mild acidic conditions (0.05–0.1 M HNO₃), the elongated morphology of H-TNFs was conserved when the crystal phase was transformed from hydrogen titanate into anatase as it is shown in the TEM images of HPT0.05 and HPT0.1 in Fig. 2B and of HPT0.1 in Fig. 2C and D, respectively. Further increase of the acid concentration (0.5–2 M HNO₃), however, resulted in disappearance of the fibre-like structures and instead, rectangular (cube-like) NPs were formed with an edge length of ∼100 nm for samples HPT0.5, HPT1 and HPT2 (Fig. 2E–G, respectively).

Fig. 2 TEM images of (A) as-prepared H-TNFs, (B) HPT0.05, (C) HPT0.1, (D) HRTEM image of HPT0.1; inset shows the area marked by red circle (E) HPT0.5, (F) HPT1, (G) HPT2, and (H) HPT4 TiO₂ products (I) HRTEM of HPT4.

The above phase and structural evolution can be explained as follows: under mild acidic conditions, the titanate – anatase transformation takes place as an in situ rearrangement of the TiO₆ building blocks due to the similar structural arrangement. This process is therefore considered as a topochemical reaction.²⁰ ESI Fig. 3A and B† illustrate the crystal structures of titanate and anatase, respectively. On the other hand, under highly acidic conditions (as it was the case for HPT0.5–HPT2) the titanate is dissolved and a dissolution-re-crystallisation process takes place to form TiO₂. Ti–OH is protonised to generate Ti–OH₂⁺ thus, due to the large amount of H⁺ ions, the dehydration process of the structures is not favoured. The other reason for the hindrance of the formation of anatase is due to the repulsive forces between Ti–OH₂⁺ and ⁺H₂O–Ti, causing the TiO₆ octahedral units mainly being arranged via edge-sharing and giving rise to the formation of corner- and edge-sharing brookite (ESI Fig. 3C) and rutile (ESI Fig. 3D†) polymorphs.²³ The sample HPT0.1 was found to show interesting structural characteristics where the two reaction mechanisms (topochemical acid catalysed dehydration and dissolution – re-crystallisation) took place simultaneously. As a consequence of that rectangular NPs were also observed besides the nanofibres. It was found from HRTEM image (Fig. 2D) that the crystal structure was brookite (d₁₁₁ = 0.346 nm) and anatase (d₁₀₁ = 0.352 nm) for the nanocubes and for the nanofibres, respectively.

In the case of HPT4, where extremely acidic medium was used, the morphological features were significantly different from those observed for the previous samples. HPT4 showed flower-like assemblies with a length of ca. 1 μm. These structures were found to be built of radially aligned nanowires with a length of ∼0.8–1 μm and a width of ∼15 nm (Fig. 2H). HRTEM image shows that the thinner fibres were epitaxially attached to each other (Fig. 2I) as a result of dehydration and consecutive rearrangement and splitting of titanate nanostructure along the connecting corners of four TiO₆ repeating units.²⁹ The lattice distance was read as d = 0.346 nm from the inverse FFT image (not shown here) and was assigned to the (111) plane of brookite (Fig. 2I).

Fig. 3 shows the Raman spectra of the HPT0.05–4 TiO₂ samples. The characteristic Raman bands of anatase at 144 (E_g), 198 (E_g), 397 (B1g), 516 (A1g, B1g) and 639 cm⁻¹ (E_g) were recognized in HPT0.05, confirming the presence of pure anatase phase in the sample. For HPT0.1, weak vibrational bands of brookite were also visible at 247 and 322 cm⁻¹ besides anatase. When higher acid concentration was used (≥0.5 mol L⁻¹), the sharp vibrational band at 144 cm⁻¹ slightly shifted towards 153 cm⁻¹, representative for brookite.³⁰ Further vibrational peaks, assigned to brookite, were observed at 172, 214, 247, 288, 322, 366, 396, 454, 585 and at 636 cm⁻¹ in HPT0.5, HPT1, HPT2 and HPT4. Finally, in HPT1, HPT2 and HPT4 samples obtained at extreme low pH (below pH ∼1.1), vibrational Raman modes for rutile were also found besides anatase and brookite with wide bands at 143, 235 and 320 cm⁻¹ and sharp bands at 449 and 610 cm⁻¹.³¹

Fig. 3 Raman spectra of HPT TiO₂ samples. A, B and R are referring to the representative vibrations of anatase, brookite, rutile, respectively.

Raman microscopy measurements were further combined with the BTEM® algorithm as a complementary experiment to PXRD to study the crystal phase compositions. This analysis provides not only the qualitative and semi-quantitative comparison, but also the dispersion of different crystal phases in different regions of the powder samples. The obtained concentration maps, showing the relative amount of polymorphs, revealed different patterns for the samples prepared in low and in highly acidic medium. The experimental details, steps of generating data and the results are shown in ESI (SI Fig. 4–9).† It was observed that the samples of HP0.05, HPT0.1 and HPT0.5 showed relatively homogeneous distribution of the respective phases regardless of the composition of crystal structure and the morphological features, while HPT1, HPT2, and HPT4 showed spatial separation of the polymorphs. The presence of these heterojunctions between the different phases may contribute to the electron transport,^8,9 while the observed pattern in spatial arrangement or obvious phase separation may negatively affect the PEC and PC properties of these samples which will be discussed later.

The textural properties of the TiO₂ samples were analysed using the N₂-sorption method. Specific surface area data were obtained using BET (Brunauer–Emmett–Teller) method. Volume and average diameter of pores were determined by BJH (Barrett–Joyner–Halenda) and the data are summarised in Table 2. The specific surface areas varied between 52.0 and 65.4 m² g⁻¹ without significant difference.

Table 2 BET surface areas, pore volume and pore size values of the prepared TiO₂ samples

Sample ID	a^sBET (m^2 g^−1)	Vol. of pores^a (cm^3 g^−1)	Diameter of pores^b (Å)
a BJH desorption cumulative volume of pores (17 000–3 000 000).b BJH desorption average pore diameter (4V/A).
HPT0.05	65.4	0.32	203
HPT0.1	62.2	0.30	191
HPT0.5	64.5	0.42	245
HPT1	52.0	0.32	235
HPT2	52.6	0.20	136
HPT4	57.0	0.12	162

---

3.2. Optical properties and PEC vs. PC behaviours of the TiO₂ samples

The band gap energy (E_g) values of the photocatalysts were obtained from the UV-Vis diffuse reflectance spectra. Absorption coefficients (α_KM) were obtained from the reflectance spectra using the Kubelka–Munk function (Fig. 4) according to eqn (1), where α_KM stands for the absorption coefficient and R_∞ the reflectance of an infinitely thick sample with respect to a reference at each wavelength.²⁵

Fig. 4 Kubelka–Munk plots of HPT samples.

The E_g values (Table 3) were determined from the tangent lines plotted at the modified Kubelka–Munk functions versus the energy of light considering TiO₂ as an indirect semiconductor. The E_g values for HPT0.05 and HPT0.1 samples were 3.25 and 3.22 eV, respectively. These values were very close to the data reported in literature for anatase TiO₂ (3.2 eV).⁵ For samples HPT0.5 to HPT4, the band gap energy was shifted towards slightly lower energy values owing to the increasing amount of rutile and brookite which are known to have lower band gap energies, 3.02 eV³² and 3.12 eV,²⁵ respectively.

Table 3 Band gap energy (E_g) values of photocatalyst samples and corresponding wavelengths (λ), apparent reaction rate constants (k′) with linear regression coefficients (R²) of −ln(c₀/c) plot and reaction rate constant per unit surface area

Sample ID	Eg (eV)	λ^a (nm)	k (min^−1)	R^2	k′/a^sBET (g min^−1 m^−2) × 10^−4
a
HPT0.05	3.25	381.5	0.0502	0.9701	7.68
HPT0.1	3.22	385.1	0.0530	0.9770	8.52
HPT0.5	3.05	406.6	0.0372	0.9645	5.77
HPT1	3.00	413.3	0.0247	0.9638	4.75
HPT2	2.98	416.1	0.0217	0.9930	4.17
HPT4	2.98	416.1	0.0105	0.9821	1.84

---

In semiconductor photocatalysis, the rate of electron–hole generation is an important factor that impacts the photocatalytic activity. This step is essential, but still not sufficient. Once the separation is successful, the charge carriers have to reach the surface of the semiconductor NPs where they can actively participate in the photocatalytic process by generating radicals or directly interacting with adjacent organic molecules. Often the case is that these charge carriers are trapped in bulk defects before reaching the surface of the NPs.^2,33 PEC measurements, such as photo-voltammetry, are good preliminary indicators of the electronic mechanisms induced by light irradiation on the semiconductor. Fig. 5 compares linear sweep photovoltammetry data for selected TiO₂ samples (HPT0.05, HPT0.1 and HPT4 with identical film thickness). This voltammetry technique was described elsewhere.³⁴ Slow scan of the potential was recorded while the irradiation of the film was periodically interrupted. In this manner, both the “dark” and the light-induced photoresponse of the samples could be assessed in a single experiment. As seen in Fig. 5A, the photocurrents are anodic in polarity for all the samples, consistent with the n-type semiconductor behaviour of the different TiO₂ phases. The photocurrents arose mainly from the photo-oxidation of the electrolyte sulfite ions, which were the hole-scavengers (electron donors). The overall shape of the voltammograms was similar and all of them had the same onset potential. On the other hand, the magnitude of the photocurrent was notably different for the various samples. A careful comparison of the photocurrent values, detected in the plateau region, revealed an important information on the PEC properties. As seen in Fig. 5B, a volcano-type curve is obtained, which shows that the highest currents are obtained for samples HPT0.1 and HPT0.5. It is particularly interesting to correlate the maximum photocurrent values with the compositional/morphological features (as shown by XRD, Raman spectroscopy, and TEM) of the samples. The compositional change in the series of samples was reflected in the PEC behaviour. Initially, a sharp increase was observed in the photocurrents with the appearance of the brookite phase (HPT0.1 and HPT0.5). Subsequently, the photocurrent decreased with the gradual increase of the rutile component, as a larger amount of rutile could become a barrier for electron transport.¹⁵ These observations can be rationalized with the significant difference in the conductivities of the three phases (brookite > anatase > rutile).³⁵

Fig. 5 (A) Representative photo-voltammograms of selected TiO₂ samples, recorded between −1.1 V and 0.5 V, in 0.1 M Na₂SO₃, at a sweep rate of 2 mV s⁻¹ using a 300 W Hg–Xe arc lamp. (B) Comparison of the maximum photocurrent values obtained for the various TiO₂ samples.

Finally, consecutive photovoltammetric scans were conducted in a wider potential window (i.e., up to E = 1.5 V vs. Ag/AgCl) using Na₂SO₄ as electrolyte to avoid dark electrooxidation of sulfite ions (Fig. 6). In these experiments there was no hole-scavenger used in the solution; therefore, the photogenerated charge carriers stayed longer on the photoanode. These studies reveal significant differences in the stability of the various samples which was reflected by a decrease of the photocurrents in the series of voltammetric scans (as deduced from the plateau-current values). It was found that the rhomboid-shaped brookite-rich samples (HPT0.5; HPT1 and HPT2) showed a decay of the photocurrents already during the second cycle, whereas the anatase- or the rutile-rich samples showed a notable stability. These results highlight the importance of structure and morphology on the PEC properties: the rhomboid-shaped brookite-rich NPs were found to generate high photocurrents (Fig. 5B), but showed low stability of the photoresponse; whereas the elongated anatase- and rutile-rich samples had higher stability than the brookite-rich, rhomboid NPs.

Fig. 6 Different decaying behaviours of the photocurrents of the TiO₂ samples assessed by consecutive photovoltammetric scans. The scans were recorded between −0.7 V and 1.5 V, in 0.1 M Na₂SO₄, at a sweep rate of 2 mV s⁻¹ using a 300 W Hg–Xe arc lamp.

The photocatalytic activity of the samples was evaluated by following PC degradation of ethanol vapour. The reaction followed pseudo-first order kinetics and the apparent reaction rates (k′) was determined as the slope of

where c is the concentration of ethanol, c₀ is the initial concentration of ethanol and t is irradiation time. The apparent reaction rate (k′) values were normalised by the BET surface area values to compare the specific photocatalytic activity of the catalysts (Table 3). It was found that HPT0.1, the sample containing dominant anatase (93.2%) and small amount of brookite (6.8%), displayed the highest photocatalytic activity. The second most active catalyst was HPT0.05 containing pure anatase nanofibres. It was followed by the tri-crystalline (anatase, brookite and with a minor rutile phase with 49.2%; 47.7% and 3.05%, respectively) rhomboid shaped TiO₂ NPs. Furthermore, with the increasing of the rutile-content, the PC activity was decreased, accordingly.

The above observations show good correlation with the PEC properties of the different TiO₂ samples. The reason why HPT0.1 exhibited enhanced PEC properties is because of two factors. First, it is able to generate high photocurrents and second, this feature can be maintained for an extended time of irradiation. These properties are related to the advantageous structural features of this sample including the anatase-brookite bi-crystalline nature and the elongated morphology. As shown in ESI Fig. 5,† the anatase and brookite phases have fairly even spatial distribution in HPT0.1. The reason for the slightly lower PC activity of the pure anatase nanofibres (HPT0.05) should also be attributed to the absence of the bi-crystalline structure, which resulted in higher rate of recombination that accordingly led to smaller photocurrents. As for the rutile-rich samples, the generated photocurrents were very low, as rutile is not a very good conductor and it is rather difficult for the charge carriers to move in the structure. Therefore, it is not a surprise that the rutile-rich samples showed low photocatalytic activity; in spite of the fact that rutile displayed a fairly stable PEC response, it had low ability to generate photocurrents which had a detrimental effect on the PC activity. Clearly, these findings show how the structure influences and determines the PEC and PC properties, and explains why HPT0.1 is the most active TiO₂ photocatalyst among those presented in this work.

4. Conclusions

In this study, a series of anatase-, brookite- and rutile-rich TiO₂ samples crystallised in a variety of morphologies such as fibres, nanocubes and flower-like assemblies of nanowires are prepared by the acidic hydrothermal treatment of H-TNFs, and the relationship between structure, morphology, PEC and PC properties is systematically investigated. It is clearly revealed that the PEC and PC properties are closely correlated. Two aspects of PEC properties are identified with high importance: one is the ability to generate adequate amount of viable charge carriers and the other is the stability of the PEC response. A photocatalyst with prominent photocatalytic activity shall have both of these features. It is found that although a high concentration of brookite crystal phase in the samples can generate high rate of charge carriers, the photoresponse is not stable for these samples. On the other hand, the suitable proportion of 93.2% anatase and 6.8% brookite endows the sample of HP0.1 with good capability for generating charge carriers while having a stable photoresponse, leading to its highest photocatalytic activity. It is likely that the elongated morphology also contributes to the higher stability of the PEC properties. The insights in the structure–property relationships sheds light on the understanding of the catalytic mechanism and on design and development of efficient TiO₂ catalysts for photocatalytic applications.

Acknowledgements

Á. Veres and Z. Zhong are grateful to Agency for Science Technology and Research (A*STAR) Graduate Academy for financial support of this work, and Drs Armando Borgna, Paul Sharratt, Keith Carpenter for their kind support of this project. Special thanks to Drs Poernomo Gunawan, Shuying Cheng, Liangfeng Guo and Mohamed Khalid Nizamudin for the assistance in experiments and valuable discussions.

References

1. G. Rothenberger, J. Moser, M. Grätzel, N. Serpone and D. K. Sharma, J. Am. Chem. Soc., 1985, 107, 8084.
2. A. L. Linsebigler, G. Lu and J. T. Yates Jr, Chem. Rev., 1995, 95, 735.
3. M. Anpo, Pure Appl. Chem., 2000, 95, 735.
4. M. A. Fox and M. T. Dulay, Chem. Rev., 1993, 93, 341.
5. A. Scalfani and J. M. Herrmann, J. Phys. Chem., 1996, 100, 13655.
6. M. Xu, Y. Gao, E. M. Moreno, M. Kunst, M. Muhler, Y. Wang, H. Idriss and C. Wöll, Phys. Rev. Lett., 2011, 106, 138302.
7. M. Batzill, Energy Environ. Sci., 2011, 4, 3275.
8. Q. Tay, X. Liu, Y. Tang, Z. Jiang, T. C. Sum and Z. Chen, J. Phys. Chem. C, 2013, 117, 14973.
9. H. Zhao, L. Liu, J. M. Andino and Y. Li, J. Mater. Chem. A, 2013, 1, 8209.
10. M. Kaneko and I. Okura, in Photocatalysis, Science and Technology, ed. M. Kaneko and I. Okura, Kodansha Springer, Tokyo, 2002, ch. 3, pp. 30–33.
11. J. Su, X. Zou and J.-S. Chen, RSC Adv., 2014, 4, 13979.
12. L. Ye, J. Liu, Z. Jiang, T. Peng and L. Zan, Nanoscale, 2013, 5, 9391.
13. T. Li, B. Tian, J. Zhang, R. Dong, T. Wang and F. Yang, Ind. Eng. Chem. Res., 2013, 52, 6704.
14. C. H. Cho, M. H. Hana, D. H. Kim and D. K. Kim, Mater. Chem. Phys., 2005, 92, 104.
15. Y. H. Jung, K.-H. Park, J. S. Oh, D.-H. Kim and C. K. Hong, Nanoscale Res. Lett., 2013, 8, 37.
16. Z. Chen, J. Liu, S. Qiu, G. Dawson and W. Chen, Catal. Commun., 2012, 21, 1.
17. J. Chen, H. B. Yang, J. Miao, H.-Y. Wang and B. Liu, J. Am. Chem. Soc., 2014, 136, 15310.
18. C. Zha, L. Shen, X. Zhang, Y. Wang, B. A. Korgel, A. Gupta and N. Bao, ACS Appl. Mater. Interfaces, 2014, 6, 122.
19. W. Yang, Y. Xu, Y. Tang, C. Wang, Y. Hu, L. Huang, J. Liu, J. Luo, H. Guo, Y. Chen, W. Shi and Y. Wang, J. Mater. Chem. A, 2014, 2, 16030.
20. H. Zhu, X. Gao, Y. Lan, D. Song, Y. Xi and J. Zhao, J. Am. Chem. Soc., 2004, 126, 8380.
21. T.-D. N. Phan, H.-D. Pham, T. V. Cuong, E. J. Kim, S. Kim and E. W. Shin, J. Cryst. Growth, 2009, 312, 79.
22. Y.-S. Lin, D.-L. Shieh, P.-Y. Chen and J.-L. Lin, Mater. Chem. Phys., 2012, 134, 1020.
23. Y. Yu and D. Xu, Appl. Catal., B, 2007, 73, 166.
24. H. Yu, J. Yu, B. Cheng and M. Zhou, J. Solid State Chem., 2006, 179, 349.
25. D. Reyes-Coronado, G. Rodríguez-Gattorno, M. E. Espinosa-Pesqueira, C. Cab, R. de Coss and G. Oskam, Nanotechnology, 2008, 19, 145605.
26. R. W. Cheary, A. A. Coelho and J. P. Cline, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 1.
27. R. J. Hill and C. J. Howard, J. Appl. Crystallogr., 1987, 20, 467–474.
28. Y. V. Kolen'ko, K. A. Kovnir, A. I. Gavrilov, A. V. Garshev, J. Frantti, O. I. Lebedev, B. R. Churagulov, G. V. Tendeloo and M. Yoshimura, J. Phys. Chem. B, 2006, 110, 4030.
29. L. Shen, N. Bao, Y. Zheng, A. Gupta, T. An and K. Yanagisawa, J. Phys. Chem. C, 2008, 112, 8809.
30. A. D. Paola, M. Bellardita and L. Palmisano, Catalysis, 2013, 3, 36.
31. G. A. Tompsett, G. A. Bowmaker, R. P. Cooney, J. B. Metson, K. A. Rodgers and J. M. Seakins, J. Raman Spectrosc., 1995, 26, 57.
32. K. Rajeshwar and J. Ibanez, in Environmental Electrochemistry, Fundamentals and applications in pollution abatement, ed. K. Rajeshwar and J. Ibanez, Academic Press Inc, California, 1997, ch. 6, p. 541.
33. T. Koida, S. F. Chichibu, A. Uedono, A. Tsukazaki, M. Kawasaki, T. Sota, Y. Segawa and H. Koinuma, Appl. Phys. Lett., 2003, 82, 532.
34. C. Janáky, N. R. de Tacconi, W. Chanmanee and K. Rajeshwar, J. Phys. Chem. C, 2012, 116, 4234.
35. H. Tang, K. Prasad, R. Sanjinès, P. E. Schmid and F. Lévy, J. Appl. Phys., 1994, 75, 2042.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra11489b

---