Flexible AlN flags for efficient wind energy harvesting at ultralow cut-in wind speed

Abstract

Wind and fluid flow represent some of the most attractive renewable energy sources for addressing climate change, pollution and energy insecurity issues. Wind harvesting technologies, in particular, are the fastest-growing electric technologies in the world because of their efficiency and lower environmental impact with respect to traditional energy sources, despite exhibiting major drawbacks such as big infrastructure investment and environment invasiveness, producing high levels of noise and requiring the need of large areas for their installation. A single wind turbine can produce megawatts of power and they have the potential to cover the entire world’s energy demand in the next few years, but they have a technological limit in a cut-in wind speed of about 4 m s⁻¹, below which the turbines do not operate, excluding them as an energy source for slow air flows. At the same time most of the wind available in the environment is below the turbines’ threshold speed. In this paper we show that small flags, made by piezoelectric thin film on flexible polymers and whose shape resembles the dry leaves of trees, can efficiently act as harvesters of energy from wind at extremely low speed, such as from a gentle blow or breath. We demonstrate that piezoelectricity on flexible polymers is achievable by depositing a thin film of piezoelectric aluminium nitride (AlN), sandwiched between metal electrodes with columnar grains coherent through the polycrystalline layers, on Kapton substrates. The prototype flags have a natural curling due to the release of the residual stress of the layers. While the curling is essential for the activation of the maximum flag oscillation, this system is so elastic and light that oscillations start at a cut-in flow speed of 0.4 m s⁻¹, the lowest reported so far, with an open circuit peak to peak voltage of 40 mV. The voltage increases to 1.2 V when the flag is flattened and parallel to the fluid flow lines, with a generated power of 0.257 mW cm⁻³.

---

Introduction

The potential of wind energy is outstanding; a recent study shows that in 2030, 50% of the world’s energy demand could be satisfied by 3.8 million 0.5 MW wind turbines.^1,2 This huge energy potential is confirmed by the growth in the wind energy market. According to reported analysis^3,4 it is possible to say that wind energy is the energy of the future and its availability depends on how fast the wind turbine makers are able to produce them. Wind turbines can work in a wind speed range from 4–20 m s⁻¹, reaching the maximum conversion efficiency of about 40% at a wind speed of 9 m s⁻¹. The theoretical mechanical power P available from wind for a turbine with a conversion efficiency η, a cross section area A, an air flow of density ρ (= 1 kg m⁻³) and a wind speed v is:

P = 0.5Aρηv³ (1)

Wind turbines do not operate at a wind speed lower than 4 m s⁻¹. Furthermore, high wind speed regimes are very hard to find close to the ground because of friction pull, and wind turbine installations must be very tall leading to a high visual impact. In addition, the blade rotation of the tall wind turbines dramatically affects the environmental acoustic noise^5–7 and the life of birds.

Several groups worldwide are studying new approaches for reducing size, footprint and cut-in wind speed of wind energy harvesters. An interesting approach is proposed by Priya et al.,⁸ consisting of a piezoelectric windmill composed by an airscrew rotated by the wind and connected to a cam-shaft gear mechanism that, during the rotation, impacts against PZT-based piezoelectric cantilevers arranged along the circumference of the mill. The system is very compact with a cut-in speed of 2.1 m s⁻¹.

More recently Li et al.⁹ presented a harvesting system in which the wind flow impacts against a semi-rigid cantilever, which is a piezoelectric stalk equipped with a triangular gangling part that amplifies the flapping; by combining many of their harvesters, Li et al. propose a piezoelectric tree. Another interesting example of energy harvesting from fluid flows is a PVDF piezoelectric eel.¹⁰ The eel is a system composed of multiple electrodes that oscillate behind a bluff body due to the generated vortex shedding. Indeed PVDF is a good candidate for fluid energy harvesting, being a flexible piezoelectric polymer, however it is difficult to synthesize in thin films smaller than tens of microns with possible damage during poling procedures. A thickness of 26 μm and its Young modulus make the PVDF harvesters semi-rigid as well described by Sun et al.¹¹ who propose PVDF foils thinned down to 11 μm by dry etching in order to collect energy at a speed of 2 m s⁻¹, such as that from the air flow of respiration. Therefore, the conversion into electricity of the mechanical energy coming from very low speed air flows requires piezoelectric transducers to be very elastic and light. The piezoelectricity in a flexible structure is usually achieved either by exploiting a flexible piezoelectric material such as a piezoelectric polymer, or through the integration of piezoelectric crystals with a polymeric matrix/substrate.^12–14

The energy harvester proposed in this work overcomes the limits of rigidity and cut-in wind speed since it is based on a thin flexible flag of Kapton (25 μm) with stress-induced charge generated by a thin film of piezoelectric AlN sandwiched between two electrodes and placed at the flag hinge region. By virtue of its high flexibility, the harvester oscillates quite instantaneously in an air flow. An extremely low cut-in wind speed of 0.4 m s⁻¹ is achieved, far smaller than that reported so far for wind harvesters.

Experimental

Materials and methods

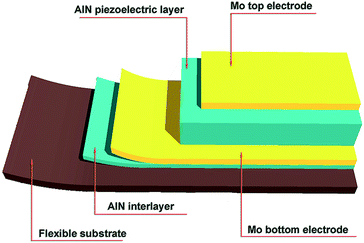
The small flag produced to convert energy from air flow is made using Kapton as a substrate for thin film deposition. A sequence of AlN (120 nm), Mo (120 nm), AlN (910 nm) and Mo (207 nm) layers are deposited on Kapton HN foil 25 μm thick (Fig. 1), attached by silicone (PDMS Sylgard 184) to a silicon wafer. The layers are deposited by sputtering in a single run in order to minimize contaminations.

Fig. 1 In the picture is shown (not proportionally) the sequence of the layers: the flexible substrate is Kapton HN with a thickness of 25 μm; the AlN interlayer (120 nm) enhances the adhesion on Kapton and promotes the columnar arrangement. Mo layers, 120 nm and 207 nm thick, are used as bottom and top electrical contact, respectively. The AlN active layer is 910 nm thick.

The deposition parameters are as follows: the first Mo layer is deposited from a high-purity (99.999%) Mo target at room temperature, with a total pressure of 1.5 × 10⁻³ mbar in an Ar atmosphere and with DC power of 500 W. The AlN layer is deposited from a high purity Al target (99.999%) with a gas mixture of N₂ (14.5 sccm) and Ar (10 sccm) at a pressure of 1.2 × 10⁻³ mbar. The sputtering plasma is generated in DC pulsed mode with a frequency of 120 kHz and a power of 2250 W. The chamber temperature increases to 250–300 °C during the reactive sputtering process, which is in the thermal working region of Kapton film. The topmost Mo layer is deposited after cooling down the chamber and in the same conditions as reported above.

The piezoelectric AlN deposited by sputtering is highly oriented along the c-axis perpendicular to the substrate regardless of the underlying amorphous state. To enhance the orientation of the texture and the adhesion of the polycrystalline structure to the polymer, an interlayer of AlN (120 nm) is deposited under the bottom electrode of Mo. In this way the AlN/Mo/AlN hetero-structure shown in Fig. 2a is very well oriented and almost continuous through the single nanograin.¹⁵

Fig. 2 (a) SEM image of the AlN/Mo/AlN/Mo stack deposited on Kapton attached to a rigid substrate with a columnar arrangement. (b) SEM of the same structure after release of Kapton from the rigid substrate and a mechanical cycle in a wind tunnel from 0 to 15.5 m s⁻¹; the film is elastically strained.

The total residual stress of the AlN and Mo layers on Kapton is compressive and it is visible as a curling of the foil when the stress is released. The thin film is deformed with a curvature radius of 3.5 mm with no cracks.

The fact that the strain occurring during flapping is elastic is ascribed to the columnar arrangement of the nanograins originating from the AlN interlayer and propagating through the molybdenum bottom electrode as far as the AlN piezoelectric layer. This structure can distribute the stress produced by the very large oscillations through the grains boundaries,^16,17 preventing the propagation of dislocations and defects. Indeed the SEM image in Fig. 2b shows the lack of plastic defects in the relaxed sample after the test in the wind tunnel at the maximum possible speed of 15.5 m s⁻¹.

The ability of AlN thin films to deform elastically is very important when the substrate is flexible, since the oscillation amplitude obtained by the model is in the range of millimeters, at least three orders of magnitude higher than the typical amplitudes achieved on a silicon-based harvester.¹⁸ The enhancement of the displacement due to the flexibility of the substrate results in a huge increase in charge generation in the AlN thin film, as already observed by Akiyama et al.¹⁹ for AlN grown on a polyimide diaphragm.

The Kapton/AlN/Mo/AlN/Mo structure is masked by the positive tone photoresist AZ5214 and dry etched by an ICP (Inductively Coupled Plasma) etching system. The etching of the Mo top electrode and the AlN active layer with the same mask is performed in a single step, using a gas mixture based on 20 sccm SiCl₄, 25 sccm N₂ and 7 sccm Ar; the power applied to the platen and to the coil are 45 Watt and 100 Watt, respectively. This etching is not selective between Mo and AlN. Afterwards, a second photolithography with the same resist is used to shape the Mo bottom electrode and the AlN interlayer with the same mask. The process is simple and compatible with common microfabrication tools used in semiconductor foundries.^20,21

After resist removal the foil is released by the support on which it was previously laminated by dipping the sample in isopropanol at room temperature for about 2 hours. Isopropanol is able to swell the PDMS layer under the Kapton foil and to detach the flag without any crack.

The compressive stress release results in a bending of the sample. The foil is cut with a width 1.5 cm and length 2.5 cm and bonded on a base with plated holes, where connectors are welded for the electrical characterization (Fig. 3).

Fig. 3 Flag prototype tested in the wind tunnel; the residual stress of the polycrystalline layers on the Kapton generates a bending of the Kapton foil.

The active area represented by the stack of piezoelectric AlN sandwiched between two molybdenum electrodes on the interlayer is positioned in order to maximize the piezoelectric thin film strain as well as the charges generated at the hinge.

A Keithley 2420 source meter is used to measure the open circuit voltage V_oc and short circuit current I_sc while the miniflag is in the wind tunnel and the air flow speed is progressively increased from 0 to 15.5 m s⁻¹. Simultaneously with the electrical parameters, the air flow speed in the tunnel is measured by a thermo-anemometer Kimo VT100, having a working range of 0–30 m s⁻¹.

2D Computational Fluid Dynamics (CFD) simulations are used to describe the experiments in a wind tunnel. A commercial software package (COMSOL inc.) using a Finite Element Method (FEM) is used to build the computational domain and the multiphysics models. Fluid-structure interaction physics is exploited in the simulations; a time-dependent solver is used in order to have, as an initial value problem, a negligible initial flow while a time step function described the flow increase up to the steady state condition. The fluid is set as air, and, for numerical calculations, it is assumed to be incompressible, and neither isothermal nor laminar. Only the continuity and momentum equations are used because heat transfer is not considered. The walls are assumed to be smooth and the standard wall conditions are applied. The distance of the piezoelectric flag apparatus from the wall in the simulation is set to 23 cm, as in the experimental setup. The flag length, protruding out of the support, is set to 20 mm. Three different kind of simulations have been realized: (a) a simple wing NACA airfoil shape (head diameter 1.4 cm; length 11.7 cm) in order to obtain a very controllable fluid pattern; (b) the flag mounted at the end of a flat box (2 mm in height and 28 mm in length); (c) the flag mounted on the previous flat box but tilted at 30°.

Results and discussion

The voltage V and the current I generated by an oscillating flag in an air flow are measured by bonding two wires to the top and bottom electrodes with a silver paste, attaching the flag on a support and positioning the active area at the hinge (Fig. 3).

The electrical characterization correlated with wind speed is performed, recording the open circuit voltage V_oc and short circuit current I_sc²² separately, by continuously increasing the wind speed in the tunnel. From Fig. 4a and b it is possible to observe that the flag starts to generate voltage quite instantaneously with V_pp around 40 mV at a cut-in speed of 0.4 m s⁻¹, and the maximum generation threshold is about 9.0 m s⁻¹. For the configuration in (a) and (b), the average power density⁸ in the region above the rated speed (10.5 m s⁻¹), is 0.257 mW cm⁻³.

Fig. 4 For the flag placed in the wind tunnel with a flow speed increasing from 0 to 15.5 m s⁻¹ and the base parallel to the flow direction (a) the generated open circuit voltage V_oc starts at a cut-in speed of 0.4 m s⁻¹ and reaches the threshold speed at 9 m s⁻¹. (b) Short circuit current I_sc.

Experimentally it is observed that the maximum generation occurs when the stressed flag is flattened. The drag coefficient C_D of a fixed flag in a uniform flow does not have a clear dependence of its bending angle with respect to the current direction:²³ it is assumed C_D = 1.5 in all configurations and consequently the drag force on the flag depends strongly on the stream velocity and flag apparent area. The drag force needed to flatten the flag is described by the formula:

F = 0.5ρ × v² × C_D × A (2)

where ρ is the medium density, v is the flow speed, C_D is the drag coefficient and A is the reference area. To demonstrate that the activation of maximum generation depends on the drag force F, we realized three different configurations and measured the voltage generated by the small flag in the wind tunnel. In case of a simple NACA (National Advisory Committee for Aeronautics) airfoil shape with the mini-flag attached on its end (Fig. 5a) in a laminar flow, the flag is completely inserted in the boundary layer. Indeed the NACA airfoil shape guarantees the minimal perturbation to the laminar flow and the curled mini-flag is parallel to the fluid flow boundary layer, with a negligible apparent projected surface with respect the impinging flow. Thus, the drag force applied on the curled flag needs a high velocity value (11 m s⁻¹) in order to completely flatten the flag and to maximize flag oscillation on its hinge (Fig. 5a, case (a)). If the curled flag and its flat support are directly inserted in the airflow (Fig. 5b), the laminar flow pattern impinges directly on the bent mini-flag surface (tilted approximately 30° with respect to the flat support). Consequently, the projected surface, apparent to the flow, is one half of its real area and, thus, the drag force applied to the flag will be one half of the intensity compared to an orthogonal direct flow against the flag. In this case the oscillation threshold velocity is approximately 9 m s⁻¹ (Fig. 5b, case (b)). Finally, when the flat support is tilted in order for the flag to be parallel to the laminar flow direction, (Fig. 5c), two cooperating mechanisms contribute together to the flag bending. Indeed, the flat support is working as a flow deflector, allowing the flow to be re-directed towards the flag (with the whole flag surface in this case almost orthogonal to the deflected drag force). While the projected surface facing the deflector decreases with bending, at the same time the surface facing the direct flow increases and a drag force is applied directly by the laminar flow on the flag: the combination of the two forces is able to maximize the oscillation of the flag at 6 m s⁻¹ (Fig. 5c, case (c)). By eqn (2) in cases (b) and (c) the drag force sufficient to overtake the elastic force due to the flag internal stress is approximately 10⁻² N.

Fig. 5 Three different flag–flux interactions are studied: (a) the base of the flag at the tip of a NACA airfoil to suppress generation of vortexes; (b) the base of the flag parallel to the flow direction; (c) the base of the flag tilted by 30° with respect to flow direction. (d) Comparison of generated voltages shows that the drag force needed to flatten the flag is determined by the reference area impinged upon by the laminar flow, and so by the relative position of the flag.

Simulations have been carried out in order to understand the role of the flow pattern at the maximum charge generation and energy harvesting regions. The initial geometry for each simulation was designed as the three configurations studied in Fig. 5 at flow speeds, and corresponding drag forces, able to flatten the flag in each configuration: flow patterns at 12 m s⁻¹ for case (a); 11 m s⁻¹ for case (b) and 8 m s⁻¹ for case (c) (Fig. 6). CFD simulations show that the voltages generated in the region above the rated speed are dependent on the flow pattern inside the wind tunnel. For cases (a) and (b) the voltage values are comparable since the flag is completely inserted inside the aerodynamic tail layer (Fig. 6a and b): the flag is constrained inside the tail, where fluid velocities are low and almost laminar. The amplitude of oscillations is 6 mm per period for the NACA airfoil shape (case a) in a period of approximately 400 ms with a flag shape maintaining a flat shape (no deformation along the flag during the oscillation is observed). In the case (b) arrangement, the flattened position is fixed at about 1.5 mm with respect to the horizontal position and longitudinal mode oscillations occur with an amplitude of hundreds of microns along the flag length in a period of about 10 ms. In contrast, in case (c), where a Karman street pattern is generated through the action of the tilted deflector, the voltage values are higher. With the flag at the boundary between low and high flow regions, where the Karman vortexes originate, a lower flow speed can efficiently induce effective oscillations and charge generation. The flag oscillations show an amplitude of about a factor of two greater than that in case (a) (about 12 mm) with a shorter period of approximately 40 ms, while small longitudinal internal oscillations are superimposed along the flag length with an amplitude of hundreds of microns in a period of about 10 ms. The vortexes generated produce larger oscillations on the flag hinge and along the flag itself, with higher voltages produced, in good agreement with the experimental results.

Fig. 6 The three different flag–flux interactions are simulated above the rated speed to show the flow patterns responsible for flag oscillations. The initial state is flag flattened along the flow when the velocity is above the rated speed region: 12 m s⁻¹ for case (a); 11 m s⁻¹ for case (b) and 8 m s⁻¹ for case (c).

Mechanical oscillations of the flag generated by Karman vortices have an impact on the stability of the system and the cut-out speed of the system. Experimentally we observed that the cut-out speed is dependent on the flag configuration: in the range between 0 m s⁻¹ and 15.5 m s⁻¹ no failure has been observed up to the maximum measurement flow speed and the cut-out wind speed is therefore at least 15.5 m s⁻¹; for the tilted configuration the devices are unaffected at speeds lower than 10 m s⁻¹. In this latter configuration, FEM simulations confirm that maximum mechanical oscillations of the flag are reached and the cut-out wind speed can be set to 10 m s⁻¹.

Conclusions

A flexible technology has been developed to harvest energy from a light air flow; the technology is based on a thin piezoelectric film of AlN deposited by sputtering on a flexible foil of Kapton. An almost continuous columnar arrangement in the crystal structure of the thin films is responsible for the inhibition of crack propagation. The flexible small flag obtained has been inserted in a laminar fluid flow with the flat support parallel to the flow, tilted at 30° and mounted at the end of a NACA airfoil shape, respectively. The device starts to generate at 0.4 m s⁻¹ and, depending on the different configuration in the fluid stream, the threshold speed for the maximum generation is 11 m s⁻¹, 9 m s⁻¹ and 6 m s⁻¹ for the NACA airfoil shape, flat and tilted support, respectively. Experimental results demonstrate that the maximum voltage generation occurs at air velocities for which the applied drag force flattens the stressed flag at 10⁻² N. CFD simulations show that the voltage generated above the rated speed region is dependent on the flow pattern produced by the configuration in the wind tunnel. A Karman vortex street has been shown as the most efficient flow pattern for energy harvesting by the flexible small flag. The design of a cut-out mechanism has not been tackled in this preliminary study since this flag has been considered for harvesting wind energy close to the ground or in pipes and interspaces, where the speed should never exceed 10 m s⁻¹. This device is produced at very low cost with a negligible environmental impact, with the synthesis being based on a plastic substrate and sputtering deposition. All these characteristics let us envision the application of this technology to collect energy both indoors and outdoors even from a breath or breeze, providing to the energy grid a constant and positive contribution with almost no visual, acoustic and environmental impact.

Acknowledgements

The authors want to acknowledge the architect Stefania Stamerra for the technology application. This research has been funded by National Italian Project PON ITEM.

Notes and references

1. N. Armaroli and B. Vincenzo, Energy Environ. Sci., 2011, 4(9), 3193–3222.
2. M. Z. Jacobson and M. A. Delucchi, Energy Policy, 2011, 39(3), 1154–1169.
3. X. Lu, M. B. McElroy and J. Kiviluoma, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10933–10938.
4. Global Wind Energy Council, Statistical data, 2011.
5. E. Pedersen and W. K. Persson, J. Occup. Med., 2007, 264(7), 480–486.
6. R. H. Bakker, E. Pedersen, G. P. Van Den Berg, R. E. Stewart, W. Lok and J. Bouma, Sci. Total Environ., 2012, 425, 42–51.
7. M. A. Nissenbaum, J. A. Jeffery and C. D. Hanning, Noise Health, 2012, 14(60), 237.
8. S. Priya, Appl. Phys. Lett., 2005, 87, 184101.
9. S. Li, J. Yuan and H. Lipson, J. Appl. Phys., 2011, 109, 026104.
10. G. W. Taylor, J. R. Burns, S. M. Kammann, W. B. Powers and T. R. Welsh, IEEE J. Oceanic Eng., 2001, 6(4), 539–547.
11. C. Sun, J. Shi, D. J. Bayerl and X. Wang, Energy Environ. Sci., 2011, 4, 4508–4512.
12. R. Agraval and H. D. Espinoza, Nano Lett., 2011, 11, 786–790.
13. S. Lee, S. H. Bae, L. Lin, Y. Yang, C. Park, S. W. Kim, S. N. Cha, H. Kim, Y. J. Park and Z. L. Wang, Adv. Funct. Mater., 2012, 23, 2445–2449.
14. J. M. Sloss, J. C. Bruch, I. S. Sadek and S. Adali, Compos. Struct., 2003, 62(3), 423–428.
15. T. Kamoara, M. Akiyama, N. Ueno and N. Kuwano, Ceram. Int., 2008, 34, 985–989.
16. M. Oring, The Materials Science of Thin Films, Academic Press, 1991.
17. M. Akiyama, N. Ueno, N. Kuwano, K. Nonaka and H. Tateyana, Appl. Phys. Lett., 2003, 82, 1977.
18. R. Elfrink, T. M. Kamel, M. Goedbloed, S. Matova, D. Hohlfeld, Y. Van Andel and R. Van Schaijk, J. Micromech. Microeng., 2009, 19(9), 094005.
19. M. Akiyama, Y. Morofuji, K. Nishikubo and T. Kamohara, Appl. Phys. Lett., 2008, 92, 043509.
20. S. Petroni, F. Guido, B. Torre, A. Falqui, M. T. Todaro, R. Cingolani and M. De Vittorio, Analyst, 2012, 137(22), 5260–5264.
21. S. Petroni, C. L. Tegola, G. Caretto, A. Campa, A. Passaseo, M. De Vittorio and R. Cingolani, Microelectron. Eng., 2011, 88(8), 2372–2375.
22. Z. Rui, L. Lin, Q. Jing, W. Wu, Y. Zhang, Z. Jiao, L. Yan, R. P. S. Han and Z. L. Wang, Energy Environ. Sci., 2012, 9, 8528–8533.
23. K. Klaka, J. D. Penrose, R. R. Horsley and M. R. Renilson, Exp. Therm. Fluid Sci., 2005, 30, 131–139.

---