Atomic approach to the optimized compositions of Ni–Nb–Ti glassy alloys with large glass-forming ability†
Abstract
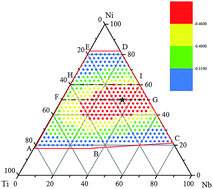
In the present study, we first constructed a long-range empirical potential for a ternary Ni–Nb–Ti system consisting of fcc, bcc and hcp metals, and then employed the verified potential in atomic simulations to study the formation of Ni–Nb–Ti glassy alloys. Atomic simulations derived a pentagon composition region of the Ni–Nb–Ti system, within which glassy alloys are inclined to form. Furthermore, the driving force for the transformation from a crystalline solid solution to a glassy alloy could be correlated to the glass-forming ability (GFA) of a particular alloy. The GFA of ternary Ni–Nb–Ti alloys with various compositions were assessed on the basis of atomic simulation results, obtaining an optimized composition region, within which the alloys possess larger GFA, as well as an optimum composition with the largest GFA. The optimum alloy is expected to be the most stable and the size of the obtainable glass may be the largest in the ternary Ni–Nb–Ti system. The optimized composition region and optimum composition could provide guidance to design the compositions of Ni–Nb–Ti metallic glasses.

 Please wait while we load your content...
Please wait while we load your content...