An outstanding second-harmonic generation material BiB2O4F: exploiting the electron-withdrawing ability of fluorine†
Rihong
Cong
*a,
Ying
Wang
a,
Lei
Kang
bc,
Zhengyang
Zhou
a,
Zheshuai
Lin
*b and
Tao
Yang
*a
aCollege of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, People's Republic of China. E-mail: congrihong@cqu.edu.cn; taoyang@cqu.edu.cn; Tel: +86-23-65105065
bBeijing Center for Crystal R&D, Key Lab of Functional Crystals and Laser Technology, Technical Institute of Physics and Chemistry, Chinese Academy of Science, P.O. Box 2711, Beijing 100080, People's Republic of China. E-mail: zslin@mail.ipc.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100049, People's Republic of China
First published on 26th December 2014
Abstract
It is well known that the incorporation of fluorine usually blue-shifts the absorption edge of a crystal due to its large electronegativity. Herein, we validate the new functionality of fluorine that leads to the strong second harmonic generation (SHG) effect in a unique nonlinear optical (NLO) bismuth borate, BiB2O4F, where F coordinates to both B3+ and Bi3+ cations. The F-incorporation not only forms a more asymmetric unit [BO3F] compared to the almost optical isotropic [BO4], but also withdraws the non-bonding electrons of Bi3+, increasing its local polarization; thus the total SHG efficiency is increased significantly. Indeed, experimental measurements and first-principles calculations both support our anticipation that BiB2O4F is a phase-matchable NLO material with an exceptionally large SHG response. In order to further consolidate the functionality of fluorine, a comparison study with the structurally similar compound BiB2O4(OH) was performed.
Introduction
Metal borates are well-known candidates for ultraviolet (UV) nonlinear optical (NLO) materials because of their tremendous structural flexibility and outstanding intrinsic physical characteristics such as high thermal stability and good transparency in the UV region.1–3 Usually, a noncentrosymmetric structure consisting of asymmetric or polar structural units exhibits a large second harmonic generation (SHG) response.4,5 For example, the large SHG effects of β-BaB2O4 and LiB3O5 are mainly contributed by the planar polyanions [B3O6]3− and [B3O7]5−, respectively.6,7 Meanwhile, the metal-centered MOx polyhedra could also make a substantial or even major contribution to SHG efficiency. Here, M could be cations with second-order Jahn–Teller distortion such as d0, d10 cations showing a polar displacement in an octahedral coordination8–11 or p-block cations with stereochemical lone pair electrons (i.e. Pb2+ and Bi3+).12–14 Apparently, a combination of the above-mentioned functional units can lead to a synergistic effect, achieving excellent SHG properties, like Cd4BiO(BO3)3, which shows an SHG response about six times that of KH2PO4 (6 × KDP).11 Pb2B5O9I is another representative showing a promising SHG performance arising from all three components, the Pb2+ cation, the I− anion, and the polyborate anion.15It is known that the introduction of halogen atoms into metal borates is beneficial to the transparency in the UV-region,16 such as KBe2BO3F (KBBF).17 Generally, F can be either coordinated to metal cations (forming M–F bonds) or boron atoms (forming B–F bonds, e.g. in the [BO3F]4− group). The former is quite usual, like KBBF,18 Pb3B6O11F2,19 and Cd5(BO3)3F.20 However, borates containing B–F bonds are rare; BaBOF3 was the first reported example,21 followed by Na3B3O3F6,22 Li2B6O9F2,23 Li2B3O4F3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 and LiB6O9F.25 Because the fluorine atom is more electronegative than the oxygen atom, it can be expected that [BO3F] is more asymmetric than the [BO4] unit. In fact, most of the above mentioned fluorooxoborates show observable SHG effects.18–20,26
24 and LiB6O9F.25 Because the fluorine atom is more electronegative than the oxygen atom, it can be expected that [BO3F] is more asymmetric than the [BO4] unit. In fact, most of the above mentioned fluorooxoborates show observable SHG effects.18–20,26
Is there another way to further enhance the SHG response rather than merely superimposing polarizations from individual functional units? Our idea is to take full advantage of the electron-withdrawing ability of the F atom, not only creating an asymmetric structural unit ([BO3F]) but also enhancing the local polarization of Bi3+ cations. BiB2O4F is a unique fluorooxoborate in which F coordinates to both boron and bismuth.27 It crystallizes in the space group P32 as shown in Fig. 1a, however, it was previously reported to be a moderate SHG material (about 1.8 × KDP), which is apparently lower than our expectation. In order to clarify this discrepancy, herein we present a re-investigation of the SHG properties of BiB2O4F by both theoretical and experimental methods. Our first-principles calculations suggested a very strong SHG effect of BiB2O4F (>10 × KDP), which was further validated by the re-measured optical properties. Furthermore, the comparison between the SHG properties of BiB2O4F and its structurally similar compound BiB2O4(OH) helps us to understand the function of F in NLO materials.
Experimental
Synthesis
Typically, to obtain BiB2O4F crystals, a mixture of 0.3638 g Bi(NO3)3·5H2O, 0.9275 g H3BO3 and 0.0630 g NaF with a Bi/B/F ratio of 1/20/2 was charged into the autoclave with an additional 0–0.5 mL of water. The autoclave was sealed and heated at 200 °C for 3 days. After the reaction, the product was washed with distilled water, and colorless crystals of BiB2O4F with a yield of ∼90% (based on Bi) were obtained. For the synthesis of BiB2O4(OH) (yield: ∼90%), a mixture of 0.3495 g Bi2O3 and 1.855 g H3BO3 with a Bi/B ratio of 1/20 was ground in an agate mortar, and then transferred into a 25 mL Teflon autoclave, which was sealed and heated at 220 °C for 3 days after adding 2 mL of water.The use of a bismuth source, NaF and an appropriate amount of water strongly affected the final product. For example, the utilisation of Bi(NO3)3·5H2O as the bismuth source, together with an appropriate amount of NaF, is necessary for the synthesis of BiB2O4F. BiB2O4(OH), on the other hand, can only be synthesized by using Bi2O3 as the bismuth source, and the purity of the product was sensitive to the content of water. If the added water was between 1 and 3 mL, pure BiB2O4(OH) could be obtained; if it was less than 1 mL, Bi[B4O6(OH)2]OH appeared as an impurity; if it was more than 3 mL, a mixture of BiB2O4(OH) and Bi3B5O12 formed. Here the purity of as-made BiB2O4F and BiB2O4(OH) was verified by powder X-ray diffraction (see details in the ESI†). Only phase-pure samples were used for further characterization.
Structure analysis and characterization
Single-crystal X-ray diffraction (XRD) data were collected on a Super Nova-CCD using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) at 104 K. Powder XRD data were collected to confirm the phase purity on a PANalytical X'pert diffractometer with a PIXcel 1D detector (Cu Kα, 40 kV and 40 mA). Thermogravimetric analysis (TG) was performed on a Mettler-Toledo TGA/DSC instrument under a N2 flow. The UV-Vis diffuse reflectance spectra were recorded at room temperature using a powder sample with BaSO4 as a standard (100% reflectance) on a Shimadzu UV-3100 spectrophotometer. Reflectance spectra were converted to absorbance spectra using the Kubelka–Munk function. The electronic structures and SHG coefficients for BiB2O4F and BiB2O4(OH) were calculated using the first-principles plane-wave pseudopotential method implemented in the CASTEP program.28,29 Details of the computational method are given in the ESI.†Powder SHG signals were measured using the experimental method adapted from Kurtz and Perry.30 Samples of BiB2O4F and BiB2O4(OH) were ground and sieved into different particle sizes. As a reference, a crystalline α-BiB3O6 (BIBO) sample was ground into the range of 105–125 μm. The powder sample was pressed between quartz slides and secured with a tape in a 1 mm thick aluminum holder that had a Φ8 mm hole. The holder was then irradiated with a pulsed infrared beam (970 mV, 10 ns, 1 Hz, 18 mW cm−2) from a Q-switched YAG:Nd3+ laser of 1064 nm wavelength. A cutoff filter was used to minimize the background, and an interference filter (530 ± 10 nm) was used to select the second harmonic for detection with a photomultiplier tube attached to an oscilloscope. This procedure was then repeated using BIBO (as a standard). No index-matching fluid was used in any of the experiments.
Results and discussion
Structural and electronic characteristics
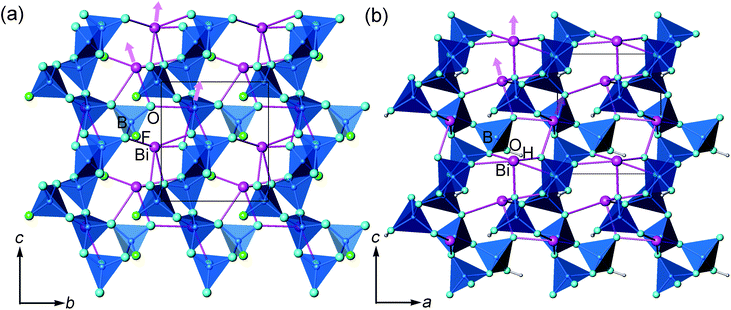
In the literature, the crystal structure of BiB2O4F was convincingly solved by the powder XRD technique in the space group P32 (a = 6.7147(1) Å and c = 6.4688(1) Å).27 Our hydrothermal synthesis leads to aggregated particles in tens of micrometers and the EDX analysis on a selected area confirms the existence of fluorine in the compound (see Fig. 2). As shown in Fig. 1a, helical borate chains in BiB2O4F, which is constructed by corner-shared borate tetrahedra (2BO4 + BO3F), are interconnected by Bi3+ to form a three-dimensional condensed structure.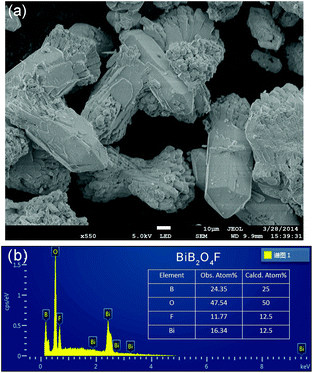 | ||
| Fig. 2 (a) SEM image and (b) EDX results for BiB2O4F. The observed atomic ratio was presented, which is consistent with the calculated value within the experimental error. | ||
In the same article reporting on BiB2O4F,27 there was another compound with the formula “Bi3[B6O13(OH)]”, possessing a highly related structure to BiB2O4F. That was also solved by the powder XRD technique but with very low symmetry, i.e. triclinic. In ref. 27, the authors claimed that the triclinic structure was a tentative (probably inaccurate) model, and during the structural refinements with powder XRD data, constraints were applied to obtain reasonable structure parameters. An exact structure determination requires single crystal X-ray diffraction. Moreover, the formula “Bi3[B6O13(OH)]” was also doubtful, because the TG weight losses observed in ref. 27 and here in our work are 2.5 and 2.77 wt% (Fig. S1 in the ESI†), respectively, which is more consistent with the formula BiB2O4(OH) (cald 2.9 wt%) rather than Bi3[B6O13(OH)] (cald 1.0 wt%).
We made an effort towards the syntheses of “Bi3[B6O13(OH)]” and obtained small single crystals, thus a single crystal XRD become possible. More than a dozen single crystals were selected for XRD data collection, and in most cases, the Rint values were quite high (>0.20), using either a triclinic or trigonal symmetry during the manual data reduction. We speculate that the very large absorption of Bi3+ to X-ray is the possible cause, especially in the case that the spatial density of Bi3+ in BiB2O4(OH) is very high.
Fortunately, we eventually obtained a suitable dataset by cracking the large crystal into pieces, and selecting a small fraction for data collection at 104 K even though only Bi3+ could be refined anisotropically, while other light atoms (boron and oxygen) were refined isotropically. The obtained atomic coordinates were chemically reasonable with regular bond distances. The final crystal structure was refined in the polar space group P31 by full-matrix least-squares refinement.31 Detailed crystallographic information is listed in Table S1.† The atomic coordinates and selected bond lengths are listed in Table S2 and S3,† respectively. The CIF file and details of the structure are also provided in the ESI.† However, there are still small residual electron densities around Bi3+, which is therefore not surprising in such a case. Overall, the currently P31, and the previously reported P1, structures are basically the same, except for a small difference in formula and the coordination of some of the boron. In fact, the higher symmetry in P31 leads to much less structural parameters, which gave a green light for DFT calculations.
For BiB2O4(OH), there are 8 crystallographically independent non-hydrogen atoms, including 1 Bi, 2 B, and 5 O (shown in Fig. 1b). All atoms locate at general positions. Coordinates for H were determined based on structural analysis and bond valence sum (BVS) calculations. Both boron atoms are coordinated by four oxygen atoms in regular tetrahedral environments. The structure of BiB2O4(OH) is very similar to BiB2O4F; the main difference is the replacement of F− by OH−, as shown in Fig. 1. Clarifying the structural similarity between BiB2O4F and BiB2O4(OH) would facilitate our further discussion about the structure–property relationship (shown later).
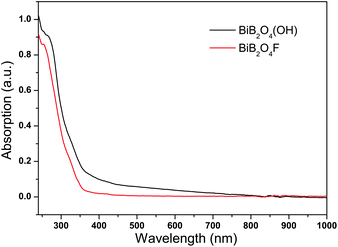
The bandgap energies for BiB2O4F and BiB2O4(OH) were estimated to be 4.43 and 4.28 eV, respectively, by the maximum peak of the first order differential curve for UV-Vis-NIR absorption spectra (see Fig. 3). No obvious absorption in the range of 350–1000 nm indicates the transparency for both samples in the entire visible region.
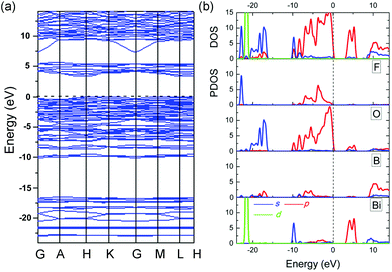
The calculated electronic band structure of BiB2O4F along the symmetry lines in the Brillouin zone of the unit cell is plotted in Fig. 4a. This structure has an indirect bandgap (3.36 eV) which is smaller than the experimental value (4.43 eV) due to the discontinuity of XC energy. Fig. 4b gives the total and partial density of states (DOS and PDOS) projected on the constituent atoms in BiB2O4F. Several electronic characteristics considering the respective groups can be summarized as follows: (i) the energy region below −10 eV is mainly composed of the isolated inner orbitals of Bi (5d), O (2s), and F (2s), which are strongly localized deeply in the valence band (VB) and have a negligible influence on the neighboring atoms; (ii) the upper VB (from −10 eV) shows large hybridization between B (2p) and O/F (2p) orbitals, but the top of the VB is mainly composed of O (2p) orbitals, which is similar to the situation in BIBO;12 (iii) the bottom of the conduction band (CB) is mostly contributed by the orbitals of Bi (6p) and O (2p). It should be emphasized that the states on both sides of the band gap are mainly composed of the orbitals from [BiO5].
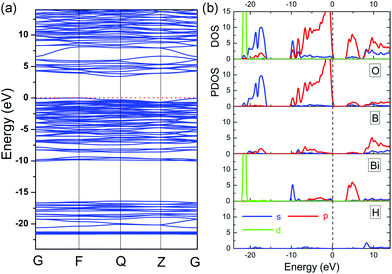
Similar to BiB2O4F, the electronic band structure, DOS and PDOS of BiB2O4(OH) are shown in Fig. 5. The theoretical energy bandgap is calculated to be 3.41 eV (indirect gap). The top of the VB is mainly composed of O (2p) orbitals and the bottom of the CB is mainly contributed by Bi (6p) and O (2p) orbitals, which is similar to the case of BiB2O4F. Additionally, the H 1s orbitals have hybridization with the electronic states on the O atoms due to the formation of hydroxyl groups, but make a rather small contribution to both VB and CB. Therefore, one can easily find that the [BiO5] group is also the major functional group in BiB2O4(OH).
Optical properties relevant to SHG output
The calculated linear refractive indices and birefringence for BiB2O4F and BiB2O4(OH) at 1064 nm are listed in Table 1. The birefringence values are slightly small, but still satisfy the phase-matching requirement for the SHG output in the IR and visible spectral regions. Since the space group is P32/P31, there are four independent non-zero SHG coefficients due to the Kleinman symmetry relationship, as shown in Table 1. The calculated SHG coefficients of BiB2O4F are much higher than that of BiB2O4(OH), and the values of d33 are significantly larger than other dij coefficients, which are −11.43 and −5.23 pm V−1 for BiB2O4F and BiB2O4(OH) respectively. Moreover, it is interesting that these values for BiB2O4F are even larger than the dij values of BIBO (expt. d22 = 2.53 pm V−1, d16 = 2.8 pm V−1, d14 = 2.4 pm V−1, d23 = −1.3 pm V−1),32 which is known as a promising SHG material in borates. Consequently, the powder SHG coefficients for BiB2O4F and BiB2O4(OH) are estimated to be 5.82 and 3.62 pm V−1 according to the Kurtz–Perry method,30 which are ∼1.77 and 1.10 times of BIBO (dpowder = 3.28 pm V−1, ∼8 × KDP).32| Calculated refractive index n and birefringence Δn at 1064 nm | Calculated SHG coefficients | PSHG effect dpowder | ||||
|---|---|---|---|---|---|---|
| n o | n e | Δn | d ij (pm V−1) | Cal. | Exp. | |
| a Powder SHG effect in BIBO is about 8 × KDP (about 3.28 pm V−1), from ref. 32. | ||||||
| BiB2O4F | 2.0699 | 2.0879 | 0.018 | d 11 = −d12 = 4.49; | 5.82 | 4.72 |
| d 16 = −d22 = 2.28 | 1.77 × BIBOa | 1.44 × BIBOa | ||||
| d 15 = d24 = 1.44 | ||||||
| d 33 = −11.60 | ||||||
| BiB2O4(OH) | 2.1570 | 2.1403 | 0.017 | d 11 = −d12 = 2.82; | 3.62 | 2.48 |
| d 16 = −d22 = 3.10 | 1.10 × BIBOa | 0.76 × BIBOa | ||||
| d 15 = d24 = 0.16 | ||||||
| d 33 = −5.23 | ||||||
Apparently, the theoretical calculations suggest excellent NLO performances for both BiB2O4F and BiB2O4(OH). In order to verify the calculations, the powder SHG effects of BiB2O4F and BiB2O4(OH) were re-measured by the Kurtz and Perry method, despite the fact that they were previously reported to be moderate in the literature.27 It should be noted that a low stability under laser irradiation was observed during the SHG measurements for both compounds. For instance, once the power density of the laser emitter increased to ≥20 mW cm−2, the powder burned from white to gray color, accompanied by a sharp decline of the SHG signal. It is well known that the output of the SHG signal increases with the enhancement of the input laser energy. Here, the final experimental data were collected by fixing the power density to be 18 mW cm−2.
Fig. 6 shows the intensities of the SHG signal of powder BiB2O4F and BiB2O4(OH) samples as a function of the particle size. It is clear that the SHG intensities increase within the range below 100 μm and then becomes almost independent of the particle size, exhibiting a typical phase-matching behavior, which is consistent with the theoretical anticipation. The further comparison with the BIBO sample (105–125 μm, as the reference) reveals that the SHG signals of BiB2O4F and BiB2O4(OH) are about 2.07 and 0.57 times of BIBO, respectively. Therefore, the experimental dpowder are estimated to be 4.72 and 2.48 pm V−1, respectively, which are smaller than our calculated values (5.82 and 3.62 pm V−1).
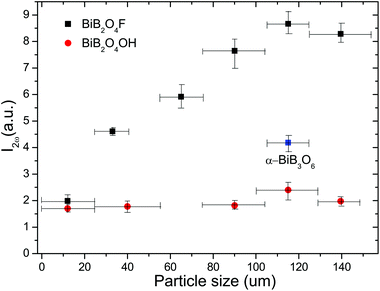 | ||
| Fig. 6 Dependence of the measured powder SHG signal intensity with the particle size of BiB2O4F and BiB2O4(OH) (α-BiB3O6 as a reference). | ||
It is reasonable that the currently measured dpowder are lower than the theoretical values, because the sieved particles for optical measurements are in fact aggregations of smaller crystallites of BiB2O4F (see the SEM images as shown in Fig. 2a). We spent months on the hydrothermal synthesis to obtain large single crystals, however all attempts failed. Nevertheless, the very strong SHG signals, especially for BiB2O4F, already validate our original anticipation that they are good NLO materials with much stronger SHG effects than the previously reported values.
Here, we should explain why there is such a large difference in SHG efficiency between our results and that in ref. 27. The previous study mainly focused on the structural chemistry of three bismuth borates, and the observable SHG output was only supporting evidence of the noncentrosymmetric structures. The authors of ref. 27 interpreted data to infer that the SHG response might come from the one-dimensional borate chains, like in the case of Pb6B11O18(OH)9, which is, however, not correct (please refer to the discussions below). As mentioned above, both BiB2O4F and BiB2O4(OH) have a low damage threshold and probably the burning phenomenon was not noticed at that time. We believe this is the major reason why a significantly low SHG effect was reported in ref. 27.
In addition, in ref. 27, they report the SHG effect based on a powder sample. We did our best to synthesize crystals. Although we did not obtain perfect and large single crystals for BiB2O4F, the average size of the crystals is tens of micrometers (see Fig. 2a). Larger crystals would give stronger SHG signals. This might be the second reason why our experiments gave a higher dpowder.
More importantly, we move on to further analyze the structure–property relationship and try to figure out the significance of the incorporation of fluorine, which may have a general instructive effect on finding new NLO materials.
Structure–property relationship
The geometrical sum of the microscopic second-order susceptibility tensors of active units determines the overall SHG coefficient of a crystal. Hence an efficient spatial arrangement of the microscopic groups will generate a relative large macroscopic SHG coefficient. In BIBO, for example, the Bi3+ cations bond to the neighbor O2− anions, forming the (BiO4)5− groups with a pyramidal shape,12 so the Bi 6s lone pair electrons “point” toward the “empty” space along the polar b-axis, indicating a strong anisotropism of (BiO4)5− (Fig. 7c). Moreover, the orientations of all (BiO4)5− groups are identical, so their microscopic second-order susceptibility tensors are simply superposed. This leads to the very large overall SHG coefficient for BIBO and the predominant contribution is from (BiO4)5− (giving almost 90% of the total value).12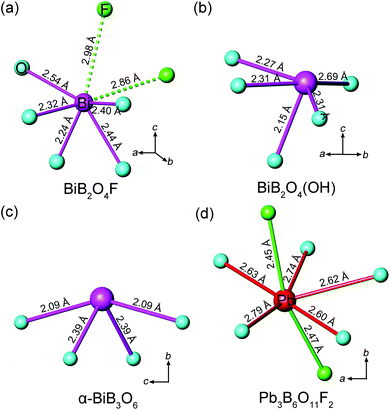 | ||
| Fig. 7 Coordination environments of Bi3+ cations in (a) BiB2O4F, (b) BiB2O4(OH), (c) α-BiB3O6, and Pb2+ cation in (d) Pb3B6O11F2. | ||
Both BiB2O4F and BiB2O4(OH) have a unique polar axis along the c-direction. Fig. 7a and 7b give the coordination environment of Bi3+ in BiB2O4F and BiB2O4(OH), respectively, which suggest that the 6s lone pair electrons are basically aligned along the c-axis. The microscopic second-order susceptibility tensors from BiO5 groups are canceled out within the ab-plane but have a superposed effect along the polar direction. The interesting question is why these two closely related structures generate largely different NLO responses, i.e. the SHG output of BiB2O4F is much stronger than that of BiB2O4(OH).
Accordingly, the respective contributions of each ionic group to the overall optical effects were investigated by adopting the real-space atom-cutting method.6 There are two crystallographically independent B atoms in BiB2O4F; one presents as [BO4], and the other is coordinated by three oxygen and one F as [BO3F] (Fig. 1). The bismuth atom is linked to five oxygen atoms by strong Bi–O bonds with the lengths of 2.24–2.54 Å (Fig. 7a). Therefore, the respective contribution of the three anionic groups, i.e., [BO4], [BO3F] and [BiO5], to the birefringence and SHG coefficients were analyzed, as shown in Table 2. The sums of the contributions from various anionic groups to the optical properties are always larger than the original total values because the oxygen ions were calculated twice in the atom-cutting procedures. It can be seen that the [BiO5] and [BO3F] groups are the main contributors to the birefringence, and the contributions are comparable.
| SHG coefficients (pm V−1) | Original | Only BO4 | Only BO3F | Only BiO5 |
|---|---|---|---|---|
| d 11 | 4.49 | 0.42 | 1.48 | 4.59 |
| d 16 | 2.28 | 0.31 | 0.81 | 1.68 |
| d 15 | 1.44 | 0.42 | −0.07 | 1.13 |
| d 33 | −11.60 | −0.65 | −2.18 | −10.91 |
| d powder | 5.82 | 0.57 (10%) | 1.50 (26%) | 5.59 (96%) |
| Δn | 0.018 | 0.008 | 0.014 | 0.016 |
For the contribution of SHG coefficients, one may easily find that the [BiO5] groups make the dominant contribution (giving ∼96% of the total value) to BiB2O4F, which is similar to the situation of BIBO. Since BiB2O4F and BiB2O4(OH) have spatial arrangements similar to those of [BiO5] and borate groups (see Fig. 1), the substitution of OH− by F− should be responsible for the stronger SHG output of BiB2O4F. First, the contribution to the total NLO response of [BO3F] groups (∼26%) is larger than that of [BO4] groups (∼10%) in BiB2O4F, because the [BO3F] tetrahedron exhibits a larger spatial anisotropy due to the partial substitution of O atoms by F atoms. More importantly, the presence of F also influences the surrounding environment of Bi3+. As shown in Fig. 7a, two F atoms were found above Bi3+ with distances of 2.86 and 2.98 Å. Fluorine is the most electronegative atom, therefore, the non-bonding electrons (6s2 electrons) of Bi3+ can be withdrawn towards two F atoms (along the c-axis) thus leading to a higher local polarization, which is beneficial to enhancing the total SHG response.
There also exists another interesting noncentrosymmetric lead borate, Pb3B6O11F2,19 which exhibits a SHG response arising from the superposing effects of the borate groups and the distorted [PbOxF2] (x = 4–6) polyhedra. The presence of F also affects the stereotactic chemistry of Pb2+. However, the F–Pb–F angles are ∼160° (Fig. 7d), and the majority of their electron-withdrawing effects on the lone pair electrons of Pb2+ are neutralized, so only a moderate SHG response was observed. Then, looking back into the case of BiB2O4F, these two F atoms locate at the same side of Bi (the F–Bi–F angle is ∼70°), indicating that their electron-withdrawing effects are synergistic. Moreover, this leads to a superior performance of BiB2O4F compared with BiB2O4(OH).
BIBO is the star compound in borate NLO materials,12,32 and was used as the reference for SHG signals in our study. From the structural viewpoint, the strong SHG effect of BIBO originates from the perfect spatial arrangement of [BiO4] groups.12 In our study, the powder SHG effect of BiB2O4F is about two times of that of BIBO, according to theoretical and experimental results. As discussed above, the incorporation of fluorine into BiB2O4F leads to a synergistic increase of local polarizations of [BiO5] and [BO3F], and hence, a very strong NLO response. In addition, the spatial density of the [BiO5] groups in BiB2O4F is about 1.33 times more than that of the [BiO4] groups in BIBO.
Conclusion
In the literature, there are numerous metal borates showing excellent UV NLO properties. Most studies are devoted to those materials with appropriate arrangements of polar structure units, which has already become the fundamental principle for NLO materials. Here in our work, we rationalize the additional function of fluorine, which is the most electronegative atom, in further enhancing the SHG efficiency by withdrawing lone pair electrons of Bi3+. In view of this, we re-investigated the SHG properties of a unique bismuth borate, BiB2O4F, where F coordinates to both B and Bi atoms. DFT calculations and experimental results both point to a very strong dpowder, even higher than the star compound BIBO. Our detailed analyses on the structure–property relationship, especially the comparison study with its relative compound BiB2O4(OH), validate our judgement on the functionality of F atoms, which may have a general instructive effect on finding new NLO materials.Acknowledgements
This work was supported by the Nature Science Foundation of China (grants 21101175, 21171178, 91222106, 91022036 and 11174297) and National Basic Research Project of China (grants 2010CB630701 and 2011CB922204). We acknowledge Prof. Z. G. Hu (Technical Institute of Physics and Chemistry, Chinese Academy of Science) for the assistance on the SHG measurements.Notes and references
- P. Becker, Adv. Mater., 1998, 10, 979–992 CrossRef CAS.
- C. Chen, Z. Lin and Z. Wang, Appl. Phys. B, 2005, 80, 1–25 CrossRef CAS PubMed.
- F. Li, X. L. Hou and S. L. Pan, Chem. Mater., 2009, 21, 2846–2850 CrossRef CAS.
- P. Shiv Halasyamani and K. R. Poeppelmeier, Chem. Mater., 1998, 10, 2753–2769 CrossRef.
- C. F. Sun, C. L. Hu and J. G. Mao, Chem. Commun., 2012, 48, 4220–4222 RSC.
- J. Lin, M. H. Lee, Z. P. Liu, C. T. Chen and C. J. Pickard, Phys. Rev. B: Condens. Matter, 1999, 60, 13380–13389 CrossRef CAS.
- Z. S. Lin, J. Lin, Z. Z. Wang and C. T. Chen, Phys. Rev. B: Condens. Matter, 2000, 62, 1757–1764 CrossRef CAS.
- H. S. Ra, K. M. Ok and P. Shiv Halasyamani, J. Am. Chem. Soc., 2003, 125, 7764–7765 CrossRef CAS PubMed.
- E. O. Chi, K. M. Ok, Y. Porter and P. Shiv Halasyamani, Chem. Mater., 2006, 18, 2070–2074 CrossRef CAS.
- Y. Inaguma, M. Yoshida and T. Katsumata, J. Am. Chem. Soc., 2008, 130, 6704–6705 CrossRef CAS PubMed.
- W. L. Zhang, W. D. Cheng, H. Zhang, L. Geng, C. S. Lin and Z. Z. He, J. Am. Chem. Soc., 2010, 132, 1508–1509 CrossRef CAS PubMed.
- Z. S. Lin, Z. Z. Wang, C. T. Chen and M. H. Lee, J. Appl. Phys., 2001, 90, 5585–5590 CrossRef CAS PubMed.
- S. H. Kim, J. Yeon and P. Shiv Halasyamani, Chem. Mater., 2009, 21, 5335–5342 CrossRef CAS.
- F. Kong, S. P. Huang, Z. M. Sun, J. G. Mao and W. D. Cheng, J. Am. Chem. Soc., 2006, 128, 7750–7751 CrossRef CAS PubMed.
- Y. Z. Huang, L. M. Wu, X. T. Wu, L. H. Li, L. Chen and Y. F. Zhang, J. Am. Chem. Soc., 2010, 132, 12788–12789 CrossRef CAS PubMed.
- H. P. Wu, S. L. Pan, K. R. Poeppelmeier, H. Y. Li, D. Z. Jia, Z. H. Chen, X. Y. Fan, Y. Yang, J. M. Rondinelli and H. S. Luo, J. Am. Chem. Soc., 2011, 133, 7786–7790 CrossRef CAS PubMed.
- B. C. Wu, D. Y. Tang, N. Ye and C. T. Chen, Opt. Mater., 1996, 5, 105–109 CrossRef CAS.
- Z. S. Lin, Z. Z. Wang, C. T. Chen, S. K. Chen and M. H. Lee, Chem. Phys. Lett., 2003, 367, 523–527 CrossRef CAS.
- H. Y. Li, H. P. Wu, X. Su, H. W. Yu, S. L. Pan, Z. H. Yang, Y. Lu, J. Han and K. R. Poeppelmeier, J. Mater. Chem. C, 2014, 2, 1704–1710 RSC.
- G. H. Zou, L. Y. Zhang and N. Ye, CrystEngComm, 2013, 15, 2422–2427 RSC.
- D. M. Chackraburtty, Acta Crystallogr., 1957, 10, 199–200 CrossRef CAS.
- G. Cakmak, T. Pilz and M. Jansen, Z. Anorg. Allg. Chem., 2012, 638, 1411–1415 CrossRef CAS.
- T. Pilz and M. Jansen, Z. Anorg. Allg. Chem., 2011, 637, 2148–2152 CrossRef CAS.
- T. Pilz, H. Nuss and M. Jansen, J. Solid State Chem., 2012, 186, 104–108 CrossRef CAS PubMed.
- G. Cakmak, J. Nuss and M. Jansen, Z. Anorg. Allg. Chem., 2009, 635, 631–636 CrossRef CAS.
- B. Andriyevsky, T. Pilz, J. Yeon, P. Shiv Halasyamani, K. Doll and M. Jansen, J. Phys. Chem. Solids, 2013, 74, 616–623 CrossRef CAS PubMed.
- L. Y. Li, G. B. Li, Y. X. Wang, F. H. Liao and J. H. Lin, Chem. Mater., 2005, 17, 4174–4180 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CrossRef CAS.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELXS 97, Program for the Solution of Crystal Structures, and SHELXL 97, Program for the Refinement of Crystal Structures, University of Göttingen, Göttingen, Germany, 1997 Search PubMed.
- H. Hellwig, J. Liebertz and L. Bohatý, Solid State Commun., 1999, 109, 249–251 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational methods, tables of crystallographic data, TG curve and SEM photo for BiB2O4(OH), powder XRD patterns for both BiB2O4(OH) and BiB2O4F. CCDC 1014612. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4qi00192c |
| This journal is © the Partner Organisations 2015 |