 Open Access Article
Open Access ArticleInvestigation of glycofullerene dynamics by NMR spectroscopy†
Olof
Engström
a,
Antonio
Muñoz
b,
Beatriz M.
Illescas
b,
Nazario
Martín
b,
Renato
Ribeiro-Viana
c,
Javier
Rojo
c and
Göran
Widmalm
*a
aDepartment of Organic Chemistry, Arrhenius Laboratory, Stockholm University, S-106 91 Stockholm, Sweden. E-mail: goran.widmalm@su.se
bDepartamento de Química Orgánica, Facultad de Química, Universidad Complutense, E-28040 Madrid, Spain
cGlycosystems Laboratory, Instituto de Investigaciones Químicas (IIQ), CSIC − Universidad de Sevilla, Av. Américo Vespucio 49, E-41092 Seville, Spain
First published on 8th July 2015
Abstract
Glycofullerenes, in which carbohydrate molecules are attached via a linker to a [60]fullerene core, facilitate spherical presentation of glyco-based epitopes. We herein investigate the dynamics of two glycofullerenes, having 12 and 36 mannose residues at their periphery, by NMR translational diffusion and quantitative 13C relaxation studies employing a model-free approach for their interpretation. The sugar residues are shown to be highly flexible entities with S2 < 0.2 in both compounds. Notably, the larger glycofullerene with longer linkers shows faster internal dynamics and higher flexibility than its smaller counterpart. The dynamics and flexibility as well as the slower translational diffusion of the larger glycofullerene, thereby favoring rebinding to a receptor, may together with its spatial extension explain why it is better than the smaller one at blocking the DC-SIGN receptor and inhibiting the infection by pseudotyped Ebola virus particles.
Introduction
Carbohydrate–protein interactions are fundamental events in many physiological and pathological processes such as cell development and differentiation, embryogenesis, inflammation, pathogen infection, tumor progression and metastasis.1,2 These interactions are weak, but in nature this fact is compensated by a multivalent interaction between several copies of the carbohydrate ligands and the corresponding receptors (lectins) leading to strong and highly selective binding.3,4 Therefore, the development of carbohydrate multivalent tools is required to understand and explore these processes. Although there are some illustrative examples where a careful design to position ligands at a precise distance on a specific scaffold has been achieved,5,6 these are scarce and most of the examples described in the literature try to explore different scaffolds in trial-and-error testing to look for the best presentation of carbohydrate ligands in order to facilitate efficient multivalent interactions with the corresponding lectins. Among these scaffolds, the most widespread ones are dendrons, dendrimers, polymers, cyclodextrins, calixarenes, gold nanoparticles and liposomes.7,8 In this context, the possibility of using a fullerene molecule as a suitable spherical platform for a globular multivalent presentation of carbohydrates has been explored, namely a [60]fullerene was used to achieve a globular presentation of carbohydrate ligands based on a Bingel hexakis-adduct functionalization strategy.9,10 Each malonate moiety is then endowed with two or six carbohydrate units, respectively, affording fullerenes bearing 12 or 36 carbohydrate entities resulting in a globular shape. Preliminary work using a cellular assay has shown that glycofullerenes of this type (compounds 1 and 2 in Fig. 1 and S1†) are able to block the DC-SIGN receptor and inhibit the infection by pseudotyped Ebola virus particles.11 Somewhat surprisingly, the concentration for inhibition of infection differs by one order of magnitude between compounds 1 and 2 (IC50 of 2 and 0.3 μM, respectively). These results highlight that, besides the importance of the number of ligands (valency), the accessibility of carbohydrate entities at the fullerene surface is of primary importance in order to interact in a suitable way with the corresponding receptors. In fact, to the best of our knowledge there has not been any study describing the disposition of ligands on the fullerene surface related to interactions with a receptor. With the aim to understand the different behavior and the influence of the flexibility of the carbohydrate groups at the surface of the fullerene, we have carried out different NMR experiments on two glycofullerenes. In particular, we have performed NMR translational diffusion measurements and quantitative 13C NMR relaxation studies. These studies provide experimental information related to structural aspects that can help in the design of multivalent systems relying on rigid scaffolds based on carbon structures and attached carbohydrate entities that are flexible.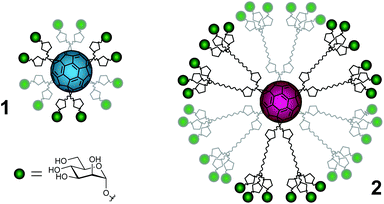 | ||
| Fig. 1 Schematic representation of the mannofullerene compounds in this study. Green spheres = α-D-mannoses, pentagons = triazoles, wavy lines = polyethylene glycol linkers and cyan or magenta spheres = [60]fullerene of 1 and 2, respectively. For a more detailed representation of the structures, see the ESI.† | ||
Results and discussion
The translational diffusion of glycofullerenes 1 and 2, which have a MW of 5.1 and 16.5 kDa respectively, was investigated by 1H NMR pulsed-field-gradient (PFG) diffusion experiments performed on samples in D2O under assumed dilute conditions (0.25 mg ml−1)12 and at a higher concentration (25 mg ml−1). The fitted diffusion coefficients (D0 and Dt, respectively) are presented in Table 1. D0 and Dt were used to calculate radii of hydration (RH,0 and RH,t) employing the Stokes–Einstein relationship, the results of which are also presented in Table 1. The change in concentration hardly affects 2, whereas an effective increase in RH by a factor of two takes place for 1 when the concentration is increased by two orders of magnitude, possibly caused by some aggregation at the higher concentration.| Glycofullerene | D 0 × 108/cm2 s−1 | D t × 108/cm2 s−1 | R H,0/Å | R H,t/Å |
|---|---|---|---|---|
| 1 | 159(7) | 90.7(5.0) | 12.5 | 21.9 |
| 2 | 74.4(2.6) | 83(0.5) | 26.7 | 24.0 |
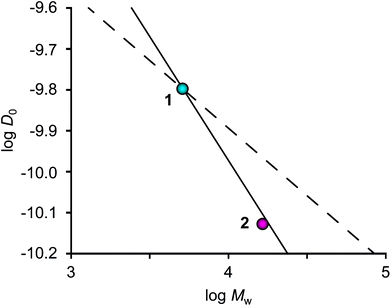
The change in translational diffusion upon generation growth in a dendrimer can provide insight into packing and solvation of the molecule. In the case of an ideal fractal dendrimer, D0 has a power dependence on the molecular weight (D0 ∝ MW−ν), with ν being the Flory exponent. Under poor solvent conditions, the growth of a dendrimer will be compact and homogeneous thus yielding a Flory exponent of ν = 0.33, which has been shown by computer simulations and scattering experiments.13 Under good solvent conditions, the growth of a dendrimer can be described as for a linear polymer (ν = 0.60) if extended linkers at low generations are assumed, but at higher generations the crowding of linkers will cause deviations.14 Analysis of D0 as a function of MW revealed the exponent ν to be 0.65 (Fig. 2), i.e. in agreement with values of ν = 0.60 and 0.67 that have been calculated for dendrimers in a good solvent utilizing Monte Carlo simulations.13,15 However, these results can be compared with our previous study of glycodendrimers where ν = 0.34 was obtained.12 The difference may be rationalized by the long linker present in glycofullerene 2, thus allowing for semidilute conditions and good solvation.15
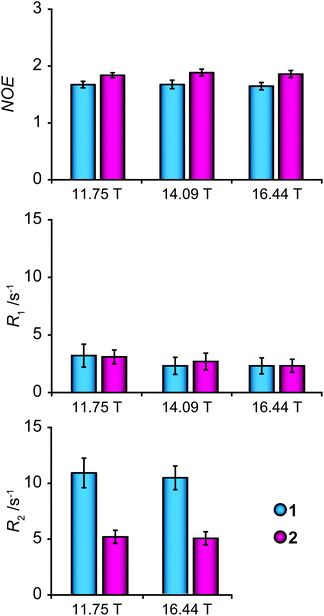
13C NMR relaxation measurements were performed on the concentrated samples, for sensitivity reasons, at three different magnetic field strengths (11.75, 14.09 and 16.44 T corresponding to 1H frequencies at 500, 600 and 700 MHz) to enable investigation of dynamic properties of glycofullerenes. The relaxation parameters R1 and R2 and the (hetero)nuclear Overhauser effect (NOE) were measured for the endocyclic carbons of the mannosyl group, in consecutive order, inversion recovery, CPMG spin-echo and dynamic NOE experiments, and the results are presented in Fig. 3 and Table S1.† A slightly smaller NOE and a considerably higher R2 relaxation rate of 1 in relation to 2 indicate that the former glycofullerene has a dynamic behavior that is more in the slow motion regime than the latter, in contrast to the results from the translation diffusion measurements. This difference may be caused by additional internal motions that influence the spectral density of the spins.
A model-free (MF) analysis was carried out to facilitate interpretation of the 13C NMR relaxation data. The computer program Relax was utilized,16,17 in which different MF approaches describing the spectral density function and different diffusion tensors are fitted to relaxation data. Solely isotropic diffusion tensors were considered due to the spherical geometry and symmetry of the glycofullerenes and τc values were fixed at values calculated from Dt. Fitting of the NMR relaxation data using an extended MF equation18 resulted in the lowest χ2red for the two glycofullerenes. In this approach the spectral density is described by three motions, namely the global rotational diffusion and two local motions, a fast and a slow one:
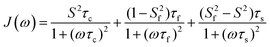 | (1) |
The global, the slow and the fast motions are described by correlation times, τc, τs and τf, respectively. The generalized order parameter (S2) describes the amplitude of the local motions (where a value of unity corresponds to the absence of local motion) and it can be bisected into S2f and S2s for the fast and the slow motions, respectively. S2 can be calculated as the product of the two other order parameters, if one assumes that the fast internal motion is axially symmetric and independent of the slow motions. Eqn (1) can be further simplified by assuming that τf is too short to have a substantial contribution to the spectral density:
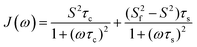 | (2) |
It has been suggested in the literature that in the case of dendrimers, the segmental reorientation that causes NMR relaxation is governed by three processes, namely (i) the overall global rotational diffusion, (ii) pulsating motions in the linker which become more prominent at the periphery and (iii) local reorientation of the segments.19 The extended MF approach seems appropriate since the model includes three motions as expected for a dendrimer-like compound. Values of S2 < 0.2 for the mannosyl groups in compounds 1 and 2 in this study indicate that the global rotational diffusion of the glycofullerene per se has a small contribution to the spectral density, which is instead governed by motions related to τs, possibly associated with the pulsating motion of the linker. The fitted τs values are of the same magnitude as the principal correlation times as found for the glycodendrimers (∼1 ns).12 Interestingly, τs is shorter in 2 than in 1 (0.25 and 0.52 ns, respectively), likely a result of the extended linker and this difference may be the underlying reason for the observation of a spectral density which is more in the fast motion regime for the former compound in relation to the latter.
It is important to include parameters of different field strengths when interpreting NMR relaxation data, as has been highlighted in the literature.20,21 The exclusion of R2 data, which had been acquired at 11.75 T, in the Relax analysis resulted in proposed models22 including Rex parameters of a large amplitude, describing motions on slower timescales. However, these results can appear from a forced fitting of parameters to a model, especially since neither R1 nor NOE is dependent on Rex. The inclusion of R2 data acquired at two different fields confirmed that Rex was an artifact of the fit.
The two mannofullerenes are able to inhibit infection by the Ebola virus in a model system by blocking the binding to the DC-SIGN receptor. Their efficiency as measured by using IC50 values differed by one order of magnitude even though the flexibility of both systems is very high with respect to the spatial presentation of the mannosyl groups, that on their own have well-defined 4C1 chair conformations on the timescales investigated herein. The binding to the tetrameric DC-SIGN receptor takes place in a Ca2+-dependent way through complexation with O3 and O4 of the mannose residue.23,24 The distance between two receptor binding sites is on the order of 40 Å.25 Thus, in order for the multivalent construct to not only bind by statistical reassociation, where the high density of ligands facilitates consecutive rebinding, the geometrical restraint has to be fulfilled in order to facilitate chelate binding at the tetrameric receptor. Furthermore, additional geometric restrains have to be invoked if binding resulting in receptor clustering should occur.
Whereas both mannofullerenes are multivalent, each linker is monovalent in compound 1 but trivalent (branched) in 2, which will result in a higher local density in the latter once binding has occurred and the process of statistical rebinding is in progress. The enthalpic term for the binding of a mannose residue in the two glycofullerenes to a receptor site should not differ and therefore the differences in the inhibition capability will be associated with other aspects. Besides the geometrical restraints essential for bridging different receptor sites the entropic costs for restraining the spacers upon binding will be different, being higher restricting the longer linker due to the larger degrees of freedom. The surface density of the ligands on the fullerenes is of importance as well as the kinetics of the rebinding process. Furthermore, once association of a ligand entity with the receptor has taken place both undesirable steric effects can take place due to incompatible ligand spacing and also beneficial steric interactions (steric stabilization) with competing virus-associated N-glycans carrying high-mannose structures may occur. The entropic loss due to long linkers can be circumvented by using a rigid core of defined length as recently reported by Ordanini et al.,6 where the length of the central rod was investigated and optimal affinity toward DC-SIGN was obtained by a combination of a rod and a short flexible linker.
The approximate spatial extensions of the two mannofullerenes 1 and 2 were investigated by construction of molecular mechanics models. These revealed that, to a first approximation, the molecular size is comparable to that determined by translational diffusion measurements, namely RH,0 = 12.5 Å and RH,0 = 26.7 Å for 1 and 2, respectively. Thus, whereas compound 1 is able to reassociate, chelate binding to a second receptor site is severely limited, if possible at all, with a diameter of <30 Å. Compound 2, on the other hand, spanning a distance >50 Å across, will be able to engage in chelate binding to another site of the tetrameric DC-SIGN receptor as well as being involved in potential receptor clustering. Although these glycofullerenes do have a rigid core of a well-defined diameter they have not been optimized as described above for the rod-containing compounds. Instead the present study reveals the very high flexibility of both systems. The larger slower moving particle 2 with even more flexible linkers resulting in a very low S2 value for the mannosyl residues arranged in a branched manner thereby facilitating rebinding26 together with its spatial extension may be the reasons for its higher efficiency when binding to the DC-SIGN receptor inhibiting the Ebola virus.
Conclusions
The extended linker facilitates good solvation of segments as such and the glycofullerene as a whole, as indicated by the Flory exponent of ν = 0.65. Also, extending the linker promotes the pulsating motion of the segment, reflected in the low Ss2 and short τs parameters of 2, consistent with relatively fast pulsating motions of a large magnitude. These molecular properties together with the spatial extension of the molecule can shed light on why 2 is an efficient multivalent inhibitor. The enhanced effect seen in the inhibition experiment of DC-SIGN may be explained by the kinetic concept of rebinding.26 Accessible binding motifs attached to flexible linkers anchored on scaffolds of slow globular diffusion (as the case for glycofullerenes) will increase the binding due to a locally increased concentration of ligands. Furthermore, the extra branches in 2, compared to 1, increase the probability of interaction.27 The rebinding mechanism is predicted to rely on low binding energy barriers of individual binding motifs (as for carbohydrates). Also, the rebinding benefits from slow translational diffusion as well as high flexibility in linkers, features that we herein show are characteristic of glycofullerene 2.Experimental
NMR samples of compounds 1 and 2 (synthesis described elsewhere9,11) were prepared by dissolving the glycofullerenes in D2O followed by treatment with Chelex 100 to remove divalent cations. Subsequent freeze-drying of the solution filtered from chelating resin was followed by re-dissolution in D2O (pD = 5) to give samples of either high concentration (25 mg mL−1) for relaxation measurements or low concentration (0.25 mg mL−1) for translational diffusion measurements. The NMR experiments were performed at 25 °C, where the temperature had been calibrated28 with a methanol-d4 sample prior to the experiments.The translational diffusion coefficients of compounds 1 and 2 were measured with pulsed-field-gradient (PFG) 1H NMR experiments on both concentrated and dilute samples. The experiments were performed on a 600 MHz Bruker Avance III NMR spectrometer equipped with a 5 mm TXI (1H/13C/31P) probe, where the Z-gradient had been calibrated to compensate for gradient inhomogeneities by using a gadolinium-doped water sample (1% H2O in D2O + 1 mg mL−1 GdCl3) with a literature value of Dt = 1.90 × 10−9 m2 s−1 for the HDO resonance.29 The diffusion time delay (Δ) was set to 60 ms and the gradient pulse length (δ) was set to 4.0 ms; each experiment was acquired with 32k data points, with gradient strengths going from 5% to 95% of maximum (55.7 G cm−1), using either 32 (concentrated sample) or 208 scans (dilute sample). The decay of the sugar bulk region integral (3–4 ppm) was used to calculate the translational diffusion coefficient by fitting a Stejskal–Tanner type equation30 to the data. The experiments were repeated four to ten times in order to obtain statistical information.
13C relaxation measurements were performed on three different NMR spectrometers operating at various field strengths, namely a Bruker Avance III 700 MHz spectrometer (16.44 T, 699.970 MHz) equipped with a 5 mm TCI Z-Gradient Cryoprobe, a Bruker Avance III 600 MHz spectrometer (14.09 T, 600.130 MHz) equipped with a 5 mm BBO probe and a Bruker Avance 500 MHz spectrometer (11.75 T, 500.130 MHz) equipped with a TCI Z-Gradient Cryoprobe. FIDs of 32k data points were recorded with either 1k or 2k scans with the carrier set in the region 70–80 ppm and spectral widths of 100–120 ppm. An exponential window function of 5 Hz and zero-filling to at least 64k data points were applied to all FIDs prior to Fourier transformation. Fast inversion recovery experiments31 were used to measure R1 relaxation rates and were performed at the three magnetic fields using an inter-scan delay of at least 3 s and six mixing times, ranging from 10 ms to 5 s, in a random order in each experiment. The relaxation rates were then fitted from the peak intensities using an in-house MATLAB (MathWorks, R2012a) script. The R2 relaxation rates were measured by the use of Carr–Purcell–Meiboom–Gill (CPMG) spin-echo experiments32 at two magnetic field strengths (11.75 T and 16.44 T), using an interscan delay of 4 s and a pulse train refocusing delay of 0.5 ms. Each experiment contained eight mixing times, ranging from 8 ms to 190 ms, which were applied in a random order, and R2 relaxation rates were calculated using the fitting routine in the vendor-supplied software Topspin 3.1. The NOE was measured at the three field strengths using the dynamic NOE experiment in pairs, with either long (2 s) or short (1 ms) irradiation and an inter-scan delay of at least 8 s. Enhancement factors were calculated as the ratio of peak intensities between the two experiments. All experiments were repeated 2–5 times from which averages and standard deviations were calculated for the NMR relaxation observables.
The model-free analysis was performed using the program Relax.16,17 Averages and standard deviations of the NMR relaxation data were used as the input and an isotropic diffusion tensor was assumed using global rotational diffusion correlation times that had been calculated from the translational diffusion coefficients33 measured by the NMR PFG diffusion experiments performed on the concentrated samples of compounds 1 and 2.
Acknowledgements
This work was supported by grants from the Swedish Research Council and the Knut and Alice Wallenberg Foundation.References
- A. Varki, Glycobiology, 1993, 3, 97 CrossRef CAS.
- Y. C. Lee and R. T. Lee, Acc. Chem. Res., 1995, 28, 321 CrossRef CAS.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2755 CrossRef CAS.
- J. J. Lundquist and E. J. Toone, Chem. Rev., 2002, 102, 555 CrossRef CAS PubMed.
- P. I. Kitov, J. M. Sadowska, G. Mulvey, G. D. Armstrong, H. Ling, N. S. Pannu, R. J. Read and D. R. Bundle, Nature, 2000, 403, 669 CrossRef CAS PubMed.
- S. Ordanini, N. Varga, V. Porkolab, M. Thépaut, L. Belvisi, A. Bertaglia, A. Palmioli, A. Berzi, D. Trabattoni, M. Clerici, F. Fieschi and A. Bernardi, Chem. Commun., 2015, 51, 3816 RSC.
- B. T. Houseman and M. Mrksich, Host–Guest Chem., 2002, 218, 1 CAS.
- S.-K. Choi, Synthetic Multivalent Molecules: Concepts and Biomedical Applications, John Wiley & Sons, Inc, New Jersey, USA, 2004 Search PubMed.
- J.-F. Nierengarten, J. Iehl, V. Oerthel, M. Holler, B. M. Illescas, A. Muñoz, N. Martín, J. Rojo, M. Sánchez-Navarro, S. Cecioni, S. Vidal, K. Buffet, M. Durka and S. P. Vincent, Chem. Commun., 2010, 46, 3860 RSC.
- M. Sánchez-Navarro, A. Muñoz, B. M. Illescas, J. Rojo and N. Martín, Chem. – Eur. J., 2011, 17, 766 CrossRef PubMed.
- J. Luczkowiak, A. Muñoz, M. Sánchez-Navarro, R. Ribeiro-Viana, A. Ginieis, B. M. Illescas, N. Martín, R. Delgado and J. Rojo, Biomacromolecules, 2013, 14, 431 CrossRef CAS PubMed.
- R. Novoa-Carballal, E. Säwén, E. Fernandez-Megia, J. Correa, R. Riguera and G. Widmalm, Phys. Chem. Chem. Phys., 2010, 12, 6587 RSC.
- S. Rathgeber, T. Pakula and V. Urban, J. Chem. Phys., 2004, 121, 3840 CrossRef CAS PubMed.
- J. S. Klos and J. U. Sommer, Macromolecules, 2009, 42, 4878 CrossRef CAS.
- L. Lue, Macromolecules, 2000, 33, 2266 CrossRef CAS.
- E. J. d'Auvergne and P. R. Gooley, J. Biomol. NMR, 2008, 40, 107 CrossRef PubMed.
- E. J. d'Auvergne and P. R. Gooley, J. Biomol. NMR, 2008, 40, 121 CrossRef PubMed.
- G. M. Clore, A. Szabo, A. Bax, L. E. Kay, P. C. Driscoll and A. M. Gronenborn, J. Am. Chem. Soc., 1990, 112, 4989 CrossRef CAS.
- D. A. Markelov, S. V. Lyulin, Y. Y. Gotlib, A. V. Lyulin, V. V. Matveev, E. Lahderanta and A. A. Darinskii, J. Chem. Phys., 2009, 130, 044907 CrossRef PubMed.
- E. Meirovitch, Y. E. Shapiro, A. Polimeno and J. H. Freed, J. Phys. Chem. A, 2006, 110, 8366 CrossRef CAS PubMed.
- L. F. Pinto, J. Correa, M. Martin-Pastor, R. Riguera and E. Fernandez-Megia, J. Am. Chem. Soc., 2013, 135, 1972 CrossRef CAS PubMed.
- A. M. Mandel, M. Akke and A. G. Palmer III, Biochemistry, 1996, 35, 16009 CrossRef CAS PubMed.
- S. Menon, K. Rosenberg, S. A. Graham, E. M. Ward, M. E. Taylor, K. Drickamer and D. E. Leckband, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11524 CrossRef CAS PubMed.
- S. Cecioni, A. Imberty and S. Vidal, Chem. Rev., 2015, 115, 525 CrossRef CAS PubMed.
- N. Varga, I. Sutkeviciute, R. Ribeiro-Viana, A. Berzi, R. Ramdasi, A. Daghetti, G. Vettoretti, A. Amara, M. Clerici, J. Rojo, F. Fieschi and A. Bernardi, Biomaterials, 2014, 35, 4175 CrossRef CAS PubMed.
- M. Weber, A. Bujotzek and R. Haag, J. Chem. Phys., 2012, 137, 054111 CrossRef PubMed.
- P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271 CrossRef CAS PubMed.
- M. Findeisen, T. Brand and S. Berger, Magn. Reson. Chem., 2007, 45, 175 CrossRef CAS PubMed.
- P. Damberg, J. Jarvet and A. Gräslund, J. Magn. Reson., 2001, 148, 343 CrossRef CAS PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288 CrossRef CAS PubMed.
- D. Canet, G. C. Levy and I. R. Peat, J. Magn. Reson., 1975, 18, 199 CAS.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688 CrossRef CAS PubMed.
- W. S. Price, Concepts Magn. Reson., 1997, 9, 299 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ob00929d |
| This journal is © The Royal Society of Chemistry 2015 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)