Novel hollow all-carbon structures

Abstract

A new family of cavernous all-carbon structures is proposed. These molecular cage structures are constructed by edge subdivisions and leapfrog transformations from cubic polyhedra or their duals. The obtained structures were then optimized at the density functional level. These hollow carbon structures represent a new class of carbon allotropes which could lead to many interesting applications.

---

1. Introduction

Graphene is a hexagonal two-dimensional (2D) lattice connected by trivalent vertices representing sp² carbon atoms. This simple network can be modified by introducing different atoms or more complex molecular units for the vertices, and/or by edge extensions and modifications such as adding extra atoms or replacing them by molecular units with incoming and outgoing bonds lying on straight lines.^1–4 Alternatively, one could also work with its dual, i.e., a triangulated planar surface of hexagonal symmetry containing vertices of degree six, and modify its topology accordingly. There are many different combinations and alterations possible to form such 2D molecular networks, which remain mostly unexplored and could have many interesting electronic properties and applications.^2,3

Graphyne shown in Fig. 1 represents such a class of 2D all-carbon allotropes,^4–6 that is either built from a graphene template or its dual, and some building blocks have already been synthesized by organic chemists.^7–13 Graphynes are one carbon atom thick and consist of sp and sp² hybridized carbons in contrast to graphene whose 2D structure consists of six-membered rings of sp² hybridized carbons. The α-graphyne structure is formally obtained by inserting –C≡C– units into every carbon–carbon bond of graphene leading to a 2D carbon structure consisting of large hexagonal rings with frustrated three-coordinated carbons in each corner of the 18-membered hexagonal carbon rings. This bond assignment reflects well the symmetry of the structure and approximate bond lengths; however, configurations with only paired electrons are likely to contribute significantly to the electronic structure. The β-graphyne structure consists of similar hexagonal rings as in α-graphyne. However, each of the hexagonal rings is surrounded by six hexadehydro[12]annulene rings yielding an infinite 2D structure with all carbons formally four-valent. The γ-graphyne structure also shown in Fig. 1 consists of an infinite 2D structure with the six-membered hexagonal carbon (benzoic) rings surrounded by six hexadehydro[12]annulene rings having all carbons four-valent as in β-graphyne. It can be easily seen that this structure can be obtained by replacing certain edges in graphene with acetylene units (in graph theoretical terms this is called an edge subdivision), or alternatively by replacing all vertices in the dual triangulated network with benzene units and edges between them with –C≡C– groups. Graphdiynes are derived from the corresponding graphyne structures by replacing the –C≡C– groups with –C≡C–C≡C– units. Graphdiyne films have been synthesized on copper surfaces.¹⁴ The graphyne and graphdiyne structures are shown in Fig. 1. Of course, there are many other graphyne structures possible, see for example Peng et al. for a recent review.⁴

Fig. 1 The molecular structure of (a) α-graphyne, (b) β-graphyne, (c) γ-graphyne and (d) γ-graphdiyne.

The graphene structure consisting of an infinite 2D layer of six-membered rings can be wrapped onto a sphere to give cavernous fullerene-like structures,¹⁵ but with the condition that e.g., 12 six-membered rings are replaced by five-membered ones such that Euler's polyhedral formula is fulfilled.¹⁶ Carbon nanotubes are similarly obtained by rolling up graphene sheets onto a cylinder.¹⁷ Fullerenes, carbon nanotubes, and other carbon-based nanostructures such as graphyne, graphdiyne, graphone, and graphane have been proposed as basic building blocks for a variety of interesting nanotechnological applications.^4,18–30 As for graphene, hollow graphyne and graphdiyne structures can be obtained by wrapping up graphyne sheets, with modifications of course so that Euler's polyhedral formula is fulfilled. Analogously, graphyne-based and graphdiyne-based carbon nanotubes can be obtained by rolling up the corresponding planar sheets. Fullerene like graphynes (fullerynes) were already introduced by Baughman et al. in 1993,²⁹ and more generally, vertex insertions into cubic polyhedral graphs were already discussed by Fowler and Rogers in 1998.³⁰ Here we also note that the insertion of dicarbon units into all bonds of a chemical structure leads to the concept of carbomers (see for example the study of Chauvin and co-workers^31–33).

One of the smallest members of this class of molecules is the recently proposed gaudiene molecule, which is an all-carbon molecule consisting of 72 carbon atoms forming a hollow structure of O_h symmetry (Fig. 2). Gaudiene can be constructed from a truncated octahedron with two thirds of the edges replaced by –C≡C– units.³⁴ Quantum chemical calculations showed that β-C₇₂ is an aromatic molecule with a rather large optical gap. Here, a novel class of hollow carbon structures is proposed. We call this class of polyhedral molecules gaudienes, because the initial polyhedron was inspired by the work of the Spanish architect Antoni Gaudí.³⁴ Gaudienes are more general than carbomers as the insertion of dicarbon units may not take place in every chemical bond.

Fig. 2 The molecular structure of β-C₇₂ of O_h symmetry, the smallest β-gaudiene investigated.

2. Graph theoretical considerations

Before we start with the discussion of the different gaudienes we briefly analyze their topology and introduce a classification scheme. For the moment we do not distinguish between single, double or triple bonding in the polyhedral graph. Formally, gaudienes belong to the class of convex polyhedra (although a quantum theoretical treatment might end up with a locally non-convex structure).³⁵ The classification of (non-regular) polytopes is currently an open problem.³⁶ For the special class of fullerenes a face-spiral classification scheme has been developed by Manolopoulos et al.,^37,38 which can be generalized for cubic polyhedra.^35,39 Here, we use the fact that simple insertions (deletions) of divalent vertices into edges (edge subdivisions) of a graph G results in a graph G′ (which is homeomorphic to G) with a larger vertex set. Note that even though we have a homeomorphism between G and G′, G is not a subgraph of G′ as the vertex set E is not a subset of E′.

A polyhedral graph G satisfies Euler's polyhedral formula, and by using the handshaking lemma we obtain

where N is the number of vertices in the graph G, E is the number of edges, F is the number of faces, N_n is the number of n-valent vertices, and F_n is the number of n-gons. We see that for n = 2 the number of divalent vertices is exactly cancelled by the number of extra edges introduced into the graph. In all cases considered here the graph G is cubic, i.e., contains only 3-valent vertices, and Euler's polyhedral formula for the face count becomes.³⁵

Thus, we conclude that one cannot tile a sphere with hexagons only, i.e., one has to introduce extra n-gons (for example 12 pentagons for fullerene graphs; this however does not guarantee that a certain polyhedron exists as for example the fullerene C₂₂ does not exist). Introducing extra n-gons can be done in many different ways as we shall see when we discuss the gaudienes in detail.

For the characterization of the various gaudienes we have to describe the cubic graph G or, if G is obtained by some other graph transformation T of the original graph G₀, i.e., G = T(G₀). We list the vertices and faces according to Pedersen³⁶ and describe the subsequent list of vertex insertions into the edges of each n-gon separately. For G, or G₀ with no divalent vertices, we use the notation

PG[N₃, N₄, N₅, N₆,…; F₃, F₄, F₅, F₆,…] (3)

where PG is the ideal point group of the polyhedron.³⁵ For example, the well known fullerene I_h-C₆₀ is characterized by

I_h[60;0, 0, 12, 20] (4)

This scheme does not uniquely classify the graph, as there are, for example, many non-isomorphic structures for a fullerene with a certain vertex count and symmetry,³⁵ but becomes useful for the gaudienes introduced here as we shall see.

α-Graphyne based polyhedral structures (in their most general form) can be derived from any polyhedral graph by inserting linear –C≡C– units into every bond (see Fig. 1). It is thus identical to the carbomer concept. This insertion is performed irrespective of the assignment of double bonds in the original structure. For cubic graphs this scheme was already introduced by Fowler and Rogers.³⁰ We denote the transformed version of a graph G₀ according to this scheme as G = α(G₀). For example, if we chose as the graph G₀ of an α-gaudiene a fullerene with N₀ vertices, denoted as PG[N₀; 0, 0, 12, (N₀/2–10)] and we insert two divalent vertices into all 3N₀/2 edges, we get a total vertex count of N_G = 4N₀, where N_G is the number of vertices in the α-gaudiene. Such an edge subdivision conserves the point group of G₀.

It follows from Thurston's proof, which considers the number of non-isomorphic triangulations of a sphere with all N vertices of valency six or smaller, that the number of nonisomorphic cubic graphs with faces up to hexagons grow as .⁴⁰ As every polyhedral graph can be transformed into an α-gaudiene, we can estimate the number of derived α-gaudienes.

β-Graphyne analogue carbon cages can be generated starting with any polyhedral (i.e., three connected and planar) graph G₀. First we perform a leapfrog transformation (LF), which is a (1,1) Goldberg–Coxeter transformation.^35,41 The Goldberg–Coxeter transformation of a polyhedral graph is a polyhedral graph itself, implying that the initial graph can be subjected to any number of consecutive leapfrog transformations. In the obtained graph all faces with sizes ≠6 and a subset of all hexagons are selected, such that each vertex is adjacent to exactly one selected face. Such a selection is guaranteed to exist and to be unique for every polyhedral graph that is obtained through a leapfrog transformation. The edges of all selected faces (i.e., two thirds of all edges) are then replaced by a linear segment with two vertices. The leapfrog transformation triples the number N₀ of vertices of a graph and introduces N₀ extra hexagons,³⁸ while the described replacement triples the number of vertices again. Therefore, β-graphyne cages with N_G = (3 × 3)N₀ vertices are accessible from polyhedra with N₀ vertices. We denote this sequence of one leapfrog transformation and the following edge subdivision of G₀ as β(LF(G₀)). We denote k consecutive leapfrog transformations of a graph G₀ as LF^k(G₀).

Equivalently, β-graphynes can be created from the same original graph G₀ by first taking its dual G^*₀. Then, each n-valent vertex in the triangulation is replaced by an n-gon in which into each edge a –C≡C– unit has been inserted. For every pair of vertices connected by an edge in the original graph, the resulting two expanded polygons are connected by an edge.

In a similar fashion, γ-graphyne analogue carbon cages are generated starting with any polyhedral graph G₀. Transformation and selection of faces are performed in the same fashion as above. Then, all edges that are not adjacent to any selected face (one third of the edge set), i.e., the complement of the previously picked edges, are replaced by two additional vertices. This replacement scheme doubles the number of vertices, transforming the polyhedral graphs with N₀ vertices into N_G = (3 × 2)N₀ vertex cages. Analogously to the previous transformation this is denoted as γ(LF(G₀)).

Alternatively, we can start with the dual graph G^*₀, and replace every n-valent vertex by an n-gon. These n-gons are then connected – according to the connectivity of the vertices they originated from – by bonds into which –C≡C– units have been inserted.

The α-, β-, and γ-graphdiyne like cages are generated in the same way as the respective graphynes but by replacing the edges with linear four-vertex segments instead of two-vertex segments. N₀ vertex polyhedral graphs are then transformed into N_G = 7N₀, N_G = (3 × 5)N₀, and N_G = (3 × 3)N₀ vertex cages respectively. Transformations of graph G₀ to graphdiynes are written with a prepended ‘C₄’, e.g., C₄-α(G₀).

3. Computational methods

Computationally, all structures were generated with a modified version of the program Fullerene.⁴² Selected small polyhedral graphs were hard coded. These graphs were subjected to leapfrog transformations as detailed in the previous section. The generation of all the gaudienes considered here is summarized in Table 1.

Table 1 Investigated gaudienes with N vertices resulting from a transformation T of an original graph G₀, i.e. T(G₀). A description of the polyhedral graph G₀ is provided as well. For one of the non-regular and less common polyhedra used we give the face spiral (FS) indices n of the n-gons for identification. For the fullerenes (Goldberg polyhedra) we provide the canonical index derived from the list of ring-spiral pentagon indices^35,37,38

N	T	G 0	Polyhedron (G0)
80	α	I h [20; 0, 0, 12]	Dodecahedron
72	β (LF)	O h [8; 0, 6 ]	Cube
216	β (LF^2)	O h [8; 0, 6 ]	Cube
648	β (LF^3)	O h [8; 0, 6]	Cube
120	C4-β (LF)	O h [8; 0, 6]	Cube
360	C4-β (LF^2)	O h [8; 0, 6]	Cube
162	β (LF)	C 2v [18; 0, 2, 8, 1]	FS (45556555545)
288	β (LF)	C2 [32; 0, 0, 12, 6]	Fullerene C32 (1)
288	β (LF)	D 2 [32; 0, 0, 12, 6]	Fullerene C32 (2)
288	β (LF)	D 3d [32; 0, 0, 12, 6]	Fullerene C32 (3)
288	β (LF)	C2 [32; 0, 0, 12, 6]	Fullerene C32 (4)
288	β (LF)	D 3h [32; 0, 0, 12, 6]	Fullerene C32 (5)
288	β (LF)	D 3 [32; 0, 0, 12, 6]	Fullerene C32 (6)
72	γ (LF)	D 6h [12; 0, 6, 0, 2]	Hexagonal prism
648	γ (LF^3)	D 6h [12; 0, 6, 0, 2]	Hexagonal prism
108	C4-γ (LF)	D 6h [12; 0, 6, 0, 2]	Hexagonal prism
432	γ (LF^2)	D 6d [24; 0, 0, 12, 2]	Fullerene C24 (1)
288	γ (LF)	D 2h [48; 0, 0, 12, 14]	Fullerene C48 (15)
288	γ (LF)	C 2v [48; 0, 0, 12, 14]	Fullerene C48 (17)
288	γ (LF)	D 2h [48; 0, 0, 12, 14]	Fullerene C48 (41)
288	γ (LF)	C 2v [48; 0, 0, 12, 14]	Fullerene C48 (56)
288	γ (LF)	C 2h [48; 0, 0, 12, 14]	Fullerene C48 (80)
288	γ (LF)	C 2v [48; 0, 0, 12, 14]	Fullerene C48 (138)
288	γ (LF)	D 6d [48; 0, 0, 12, 14]	Fullerene C48 (186)
288	γ (LF)	D 6d [48; 0, 0, 12, 14]	Fullerene C48 (189)

---

As the force field in program Fullerene can only operate on cubic graphs and triangulations, polyhedra were generated at this stage and optimized to bond lengths that correspond to the polyhedron after replacing a subset of bonds with elongated linear segments. After the optimization of the Cartesian coordinates, atoms were inserted and placed in 3D by linear interpolation.

The molecular structures were then further optimized at the density functional theory (DFT) level using the Becke–Perdew generalized gradient approximation (GGA) functional (BP86) in combination with the Karlsruhe split-valence polarization (SVP) basis sets.^43–46 Since the calculations at the BP86 level slightly underestimate the gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), single-point calculations were performed at the DFT level using Becke's three-parameter functional (B3LYP) together with a SVP basis set.^46–48 The semi-empirical dispersion correction of Grimme has been employed in the molecular structure optimization.^49,50 The DFT calculations were performed with Turbomole version 6.5.^51–53 The Cartesian coordinates of the atomic positions of all studied structures are given in the ESI.† Improving the basis set to a triple-zeta split-valence polarization set for β-C₇₂ leads only to a small change in geometry (change in bond distances |Δr_e| < 0.012 Å and bond angles |Δα_e| < 0.04 degrees). These errors are within the accuracy of DFT and therefore do not warrant more extensive computer calculations for the discussion of the structures presented here.

4. Molecular structures

4.1 α-Gaudienes

The optimized structure of the smallest fullerene-like carbomer based on α-graphyne, the gaudiene α-C₈₀, is shown in Fig. 3. The structure belongs to the icosahedral (I_h) point group as does its origin, the dodecahedron represented by the smallest fullerene I_h-C₂₀. Hence, this gaudiene consists of 12 pentagonal 15-membered carbon rings forming a cage. The atoms shared by the three rings are formally sp³ hybridized carbons with only three neighbor carbons leading to a relatively small HOMO–LUMO gap of 0.740 eV at the BP86 level, which can be compared with the HOMO–LUMO gaps of 1.66 eV, 1.45 eV and 1.23 eV for the C₆₀, C₁₈₀ and C₂₄₀ fullerenes calculated at the GGA level.⁵⁴ For comparison, DFT calculations using the BP86 functional yield HOMO–LUMO gaps of 1.24 eV and 0.21 eV for β-C₇₂ and γ-C₇₂, respectively. At the B3LYP level the HOMO–LUMO gap for α-C₈₀ is 1.22 eV. The adjacency spectrum of fullerene-like carbomers and their open/closed shell character have been analyzed in detail by Fowler and Rogers.³⁰

Fig. 3 The molecular structure of α-C₈₀ of I_h symmetry, which is the smallest α-gaudiene investigated.

A very stable molecule with a HOMO–LUMO gap of 5.17 eV is obtained by adding 20 hydrogens to the corners of the α-C₈₀ icosahedron. Larger α-gaudienes can easily be constructed by using fullerenes as templates and replacing each carbon–carbon bond with a –C≡C– moiety. All α-gaudienes have three-coordinated carbons in the intersections between three carbon rings. More stable molecules can be obtained by adding substituents to these three-coordinated carbons.

We should mention that eqn (2) also allows one to use other cubic polyhedra. For example, if we chose the truncated octahedron belonging to the Archimedean solids, O_h[24; 0, 8, 0, 6], containing six squares according to eqn (2), we can expand this graph for all edges in a similar way and we arrive at O_h-C₉₆, another type of α-gaudiene. Hence the playing field is huge for the construction of new 3D polyhedral molecular structures.

4.2 β-Gaudienes

The smallest member of the β-gaudiene class of molecules with four- and six-membered rings involved is the previously proposed β-C₇₂ shown in Fig. 2.³⁴ It belongs to the O_h point group and can be generated from the simple cube G₀ = O_h[8; 0, 6] or its dual, the octahedron G^*₀ = O_h[0, 6; 8]. When folding β-graphyne to the hollow C₇₂ structure, the edges of eight hexadehydro[12]annulene rings of β-graphyne form six four-sided rings having four carbons on each side with alternating triple and single bonds. Even though hexadehydro[12]annulene is formally antiaromatic,^55–57 β-C₇₂ is aromatic according to the ring-current criterion sustaining a ring current strength of 44.3 nA T⁻¹ around the molecule, which can be compared to the ring-current strength of benzene of 11.8 nA T⁻¹.^34,58 Since all carbons have formally four bonds, β-C₇₂ is a stable molecule with a HOMO–LUMO gap of 1.82 eV at the B3LYP/SVP level.

A number of β-gaudiene structures were constructed using small polyhedral graphs as starting points. The smallest one constructed using that procedure was β-C₁₆₂ (C_2v), which was obtained using an 18-vertex graph as the initial structure, C_2v[18; 0, 2, 8, 1], belonging to a non-regular polyhedron (see Fig. 4). This polyhedron does not belong to the common solids and we therefore give the face spiral indices in Table 1. The optimized molecular structure of β-C₁₆₂ (C_2v) is shown in Fig. 5a. It has a rather small HOMO–LUMO gap of 0.48 eV as obtained at the B3LYP level.

Fig. 4 Graph of the non-regular C_2v [18; 0, 2, 8, 1] polyhedron.

Fig. 5 The molecular structure of the energetically lowest isomers of β-gaudienes: (a) β-C₁₆₂ (C_2v), (b) β-C₂₁₆ (O_h), (c) β-C₂₈₈ (D_3d), and (d) β-C₆₄₈ (O_h).

Since the topological method ensures that the symmetry of the seed structure is conserved, many different isomers can be constructed when the corresponding fullerene structures are available. The next larger β-gaudiene structures of O_h symmetry are β-C₂₁₆ and β-C₆₄₈, which have HOMO–LUMO gaps of 0.415 eV and 0.225 eV at the B3LYP level, respectively. These are also shown in Fig. 5.

A large number of β-gaudienes consisting of 288 carbons can be constructed by using different fullerene isomers such as those of C₃₂ as starting structures. The energetically lowest β-C₂₈₈ structure of all investigated isomers (see Table 1) belongs to the D_3d point group. The energetically lowest β-gaudiene structures obtained in this work are shown in Fig. 5. The rest of the studied β-C₂₈₈ structures are shown in the ESI.† The energetically lowest β-C₂₈₈ isomers are 48.8 kJ mol⁻¹ (D₃), 51.9 kJ mol⁻¹ (D₂), 53.2 kJ mol⁻¹ (C₂), 65.6 kJ mol⁻¹ (C₂), and 146.6 kJ mol⁻¹ (D_3h) above the D_3d structure. The β-C₂₈₈ (O_h) isomer consisting of a β-C₇₂ molecule inside β-C₂₁₆ (β-C₇₂@β-C₂₁₆) is 683 kJ mol⁻¹ above the lowest β-C₂₈₈ isomer of D_3d symmetry. The HOMO–LUMO gaps of the β-C₂₈₈ structures are in the range of 0.27–0.42 eV, with the largest gap for the most stable isomer. The two β-C₂₈₈ structures of C₂ symmetry have negative HOMO–LUMO gaps at the BP86 level.

The largest molecule considered in this study was an onion-like β-C₇₂@β-C₂₁₆@β-C₆₄₈ cluster of O_h symmetry. The structure is shown in the ESI.†

4.3 γ-Gaudienes

The smallest γ-gaudiene (γ-C₇₂) studied belongs to the D_6h point group and has a HOMO–LUMO gap of 0.519 eV. The optimized molecular structure is shown in Fig. 6. The benzoic six-membered carbon ring is surrounded by six hexadehydro[12]annulene rings that are fused at the molecular edge. The correct topology of the closed surface is ensured by the six four-membered carbon rings between the hexadehydro[12]annulenes at the edge of the molecule. The next larger γ-gaudiene structure of O_h symmetry is γ-C₄₃₂ (O_h) with a HOMO–LUMO gap of 0.491 eV. The largest γ-gaudiene studied in this work is γ-C₆₄₈, which has D_6h symmetry and a small HOMO–LUMO gap of 0.253 eV at the B3LYP level.

Fig. 6 The molecular structure of γ-C₇₂ of D_6h symmetry, which is the smallest γ-gaudiene investigated.

A large number of γ-C₂₈₈ structures were constructed with different fullerene isomers of C₄₈ as the origin graph. The energetically lowest γ-C₂₈₈ belongs to the C_2v point group. The structure of the energetically lowest γ-C₂₈₈ (C_2v) isomer is shown in Fig. 7. The structures and atomic coordinates of the remaining studied γ-C₂₈₈ clusters are shown in the ESI.† The energetically lowest γ-C₂₈₈ isomers are 44.3 kJ mol⁻¹ (D_2h), 47.8 kJ mol⁻¹ (C_2h), 160.0 kJ mol⁻¹ (D_6d), 167.5 kJ mol⁻¹ (C_2v), 287.2 kJ mol⁻¹ (C_2v), 565.5 kJ mol⁻¹ (D_2h), and 873.1 kJ mol⁻¹ (D_6d) above the lowest C_2v structure. The calculations show that there are only three low-lying γ-C₂₈₈ isomers among the studied ones.

Fig. 7 The molecular structure of the energetically lowest isomers of (a) γ-C₂₈₈ (C_2v), (b) γ-C₄₃₂ (O_h), and (c) γ-C₆₄₈ (D_6h) gaudienes.

The HOMO–LUMO gap of the lowest γ-C₂₈₈ structure is 0.36 eV at the B3LYP level, whereas the HOMO–LUMO gap of the γ-C₂₈₈ is in the range of 0.18–0.47 eV, with the largest gap for γ-C₂₈₈ (D_2h). The energetically lower isomer of D_6d symmetry has a negative HOMO–LUMO gap at the BP86 level. The molecular structure of the energetically lowest γ-gaudienes obtained in this work is shown in Fig. 7.

4.4 Graphdiyne-based gaudienes

Graphdiyne-based gaudienes are obtained by replacing the –C≡C– units of gaudienes with the twice longer –C≡C–C≡C– (C₄) group.

Even though the obtained molecules have a larger number of triple bonds, the HOMO–LUMO gap is wider than the corresponding graphyne-based molecules. The HOMO–LUMO gaps calculated at the B3LYP level are 0.877 eV, 1.356 eV, and 1.168 eV for C₄-γ-C₁₀₈, C₄-β-C₁₂₀, and C₄-β-C₃₆₀, respectively. The larger stabilization of the graphdiyne-based gaudienes can be traced back to the molecular properties of dodecadehydro[18]annulene, which is an aromatic molecule.⁵⁶ The HOMO–LUMO gap of C₄-γ-C₁₀₈ is smaller than the other two studied C₄-gaudienes due to the significantly larger bond strain of the small four-membered carbon rings at the edge of the molecule. For the C₄-β-gaudienes, the correct topology is obtained by the six 20-membered carbon rings. The molecular structures of the studied C₄-gaudienes are shown in Fig. 8. The Cartesian coordinates of the atomic positions are given in the ESI.†

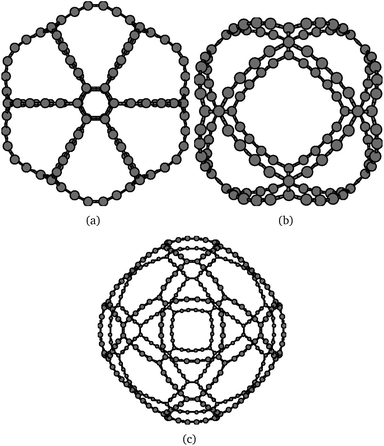Fig. 8 The molecular structure of the investigated graphdiyne-based (C₄) gaudienes: (a) C₄-γ-C₁₀₈ (D_6h), (b) C₄-β-C₁₂₀ (O_h), and (c) C₄-β-C₃₆₀ (O_h).

5. Discussion and conclusions

The γ-gaudienes are generally significantly lower in energy than the β-gaudienes for the same number of carbon atoms. The most important exception is β-C₇₂, which is 128.9 kJ mol⁻¹ below γ-C₇₂ due to the ring strain of the four-membered carbon rings of γ-C₇₂ and maybe also due to the aromatic stabilization of β-C₇₂.³⁴ The HOMO–LUMO gap of β-C₇₂ of 1.82 eV calculated at the B3LYP level is also much larger than the HOMO–LUMO gap of 0.52 eV for γ-C₇₂. For the small γ-C₇₂ cage, the bond strain of the four-membered carbon rings is not compensated by the energetically favorable structure of γ-graphyne. For larger gaudienes, the γ-graphyne structure has significantly lower energies than the corresponding β-gaudiene structures. The lowest isomer of γ-C₂₈₈ is more than 5000 kJ mol⁻¹ (!) below the energy of the lowest β-C₂₈₈ structure. For larger gaudienes, the energy difference between the γ-gaudiene and β-gaudiene is even bigger. For the largest studied gaudienes, γ-C₆₄₈ is about 11 000 kJ mol⁻¹ below β-C₆₄₈.

The relative energy per carbon atom is given as a function of 1/N in Fig. 9, where N is the number of carbon atoms. The relative energy depends roughly linearly on 1/N leading to the three straight lines in Fig. 9 showing that γ-gaudiene is the most stable structure and that C₄-gaudienes are the energetically highest ones. Extrapolation to 1/N → 0 yields the relative energy of β-graphyne, γ-graphyne, and β-graphdiyne. The calculations show that β-graphyne is 17 kJ per mol per carbon higher in energy than γ-graphyne and that β-graphdiyne is only 7 kJ per mol per carbon above β-graphyne.

Fig. 9 The relative energy (in kJ mol⁻¹) as a function of 1/N of the studied molecular classes. N is the number of atoms. The relative energies are fitted to a line. The outlier at 37 kJ mol⁻¹ for γ-C₇₂ is not considered in the fit.

The HOMO–LUMO gaps calculated at the B3LYP level are plotted as a function of 1/N in Fig. 10 yielding three straight lines for three gaudiene classes. Extrapolation of the HOMO–LUMO gap to the limit of 1/N → 0 yields the estimated HOMO–LUMO gaps of the β-graphyne, γ-graphyne and β-graphdiyne sheets. The three lines suggest that the HOMO–LUMO gaps for the infinite planar structures are larger than zero. The extrapolated HOMO–LUMO gap of β-graphyne is 0.17 eV. For γ-graphyne we obtained an extrapolated HOMO–LUMO gap of 0.33 eV. The extrapolated HOMO–LUMO gap of 1.25 eV for β-graphdiyne agrees well with the previously reported value of 1.22 eV, which was calculated at the DFT level using a hybrid functional⁵⁹ and it is significantly larger than the HOMO–LUMO gap of 0.46 eV calculated at the DFT level using the generalized gradient approximation.⁶⁰ Even though the error bars of the present extrapolated values are large due to the few number of points used in the fit, the present calculations suggest that the HOMO–LUMO gap of graphdiyne is larger than 1 eV.

Fig. 10 The HOMO–LUMO gap (in eV) as a function of 1/N of the studied molecular classes. N is the number of atoms. The relative energies are fitted to a line. The outlier at 1.82 eV for β-C₇₂ is not considered in the fit.

The hollow gaudiene structures might open the avenue to novel materials with interesting properties. For example, triple bonds provide possibilities for functionalizing the molecules with different kinds of substituents that might even couple several gaudiene molecules with polymers or solid-state materials. The gaudiene structures can also be fully or partially saturated with hydrogens without destroying their cage structures. Such molecules are ordinary saturated hydrocarbons with extraordinary hollow structures. By attaching substituents to the corners of α-gaudienes, molecules with a very large HOMO–LUMO gap are obtained. The optical gap of the C₄-gaudienes is significantly larger than the two other classes of molecules. Extrapolation to infinitely large clusters suggests that planar graphdiyne has indeed a HOMO–LUMO gap that is significantly larger than zero, which might provide novel possibilities for carbon-based mono-layered structures.⁴

Finally, we point out that there are also other graph theoretical procedures for obtaining cavernous all-carbon structures that have not been discussed here.^61,62 For example, one can insert –C≡C– units into the edges running parallel to the main axis of a fullerene nanotube. One can also use other building blocks besides carbon which fit the required topologies, e.g., building units which are used in metal–organic frameworks. This opens up a whole new area of interesting cage structures and materials which could be useful in many interesting applications.

Acknowledgements

This work has been supported by the Academy of Finland through projects (266227 and 275845) and its Computational Science Research Programme (LASTU/258258). DS acknowledges Magnus Ehrnrooth Foundation, the Swedish Cultural Foundation in Finland, and the Alexander von Humboldt Stiftung for financial support. DS also thanks the New Zealand Institute for Advanced Study at the Massey University for the kind hospitality. CSC – the Finnish IT Center for Science – is acknowledged for computer time. We would like to thank James Avery (University of Copenhagen) for providing the generalized Goldberg–Coxeter program.

References

1. H. S. S. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. N. R. Rao, Angew. Chem., Int. Ed., 2010, 122, 4153–4156.
2. A. L. Ivanovskii, Russ. Chem. Rev., 2012, 81, 571–605.
3. M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766–3798.
4. Q. Peng, A. K. Dearden, J. Crean, L. Han, S. Liu, X. Wen and S. De, Nanotechnol. Sci. Appl., 2014, 7, 1–29.
5. R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699.
6. V. Georgakilas, J. A. Perman, J. Tucek and R. Zboril, Chem. Rev., 2015, 115, 4744–4822.
7. F. Diederich, Nature, 1994, 369, 199–207.
8. M. M. Haley, S. C. Brand and J. J. Pak, Angew. Chem., Int. Ed., 1997, 36, 836–838.
9. U. H. F. Bunz, Y. Rubin and Y. Tobe, Chem. Soc. Rev., 1999, 28, 107–119.
10. E. L. Spitler, C. A. Johnson and M. M. Haley, Chem. Rev., 2006, 106, 5344–5386.
11. M. M. Haley, Pure Appl. Chem., 2008, 80, 519–532.
12. F. Diederich and M. Kivala, Adv. Mater., 2010, 22, 803–812.
13. K. Tahara, Y. Yamamoto, D. E. Gross, H. Kozuma, Y. Arikuma, K. Ohta, Y. Koizumi, Y. Gao, Y. Shimizu, S. Seki, K. Kamada, J. S. Moore and Y. Tobe, Chem. – Eur. J., 2013, 19, 11251–11260.
14. G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258.
15. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
16. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
17. S. Iijima, Nature, 1991, 354, 56–58.
18. S. Ihara and S. Itoh, Carbon, 1995, 33, 931–939.
19. M. Meyyappan and D. Srivastava, Handbook of Nanoscience, Engineering, and Technology, CRC Press, Boca Raton FL, 2003, ch. 18, pp. 1–26.
20. T. C. Dinadayalane and J. Leszczynski, Struct. Chem., 2010, 21, 1155–1169.
21. A. N. Enyashin and A. L. Ivanovskii, Phys. Status Solidi B, 2011, 248, 1879–1883.
22. R. Mas-Ballesté, C. Gómez-Navarro, J. Gómez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30.
23. D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804.
24. S. Zhang, Y. Zhang, S. Huang and C. Wang, Nanoscale, 2012, 4, 2839–2842.
25. L. Zoppi, J. S. Siegel and K. K. Baldridge, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 1–12.
26. J.-J. Zheng, X. Zhao, Y. Zhao and X. Gao, Sci. Rep., 2013, 3, 1271.
27. J. Xi, D. Wang and Z. Shuai, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 215–227.
28. Z. Li, M. Smeu, A. Rives, V. Maraval, R. Chauvin, M. A. Ratner and E. Borguet, Nat. Commun., 2015, 6, 6321.
29. R. H. Baughman, D. S. Galvão, C. Cui, Y. Wang and D. Tománek, Chem. Phys. Lett., 1993, 204, 8–14.
30. P. W. Fowler and K. M. Rogers, J. Chem. Soc., Faraday Trans., 1998, 94, 1019–1027.
31. R. Chauvin, Tetrahedron Lett., 1995, 36, 401–404.
32. R. Chauvin, Tetrahedron Lett., 1995, 36, 397–400.
33. V. Maraval and R. Chauvin, New J. Chem., 2007, 31, 1853–1873.
34. D. Sundholm, Phys. Chem. Chem. Phys., 2013, 15, 9025–9028.
35. P. Schwerdtfeger, L. N. Wirz and J. Avery, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 96–145.
36. J. J. Pedersen, Calif. Math., 1977, 2, 21–28.
37. D. E. Manolopoulos, J. C. May and S. E. Down, Chem. Phys. Lett., 1991, 181, 105–111.
38. P. W. Fowler and D. E. Manolopoulos, An Atlas of Fullerenes, Dover Publications Inc., Mineola, New York, 2nd edn, 2006.
39. L. N. Wirz, R. Tonner, J. Avery and P. Schwerdtfeger, J. Chem. Inf. Model., 2014, 54, 121–130.
40. W. P. Thurston, Geom. Topol. Monogr., 1998, 1, 511–549.
41. J. Avery, to be submitted, 2015.
42. P. Schwerdtfeger, L. Wirz and J. Avery, J. Comput. Chem., 2013, 34, 1508–1526.
43. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
44. J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822–8824.
45. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
46. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
47. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
48. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
49. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 :1–19.
51. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
52. TURBOMOLE V6.5 2013, a development of the University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
53. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
54. G. Casella, A. Bagno and G. Saielli, Phys. Chem. Chem. Phys., 2013, 15, 18030–18038.
55. J. A. Pople and K. G. Untch, J. Am. Chem. Soc., 1966, 88, 4811–4815.
56. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2001, 3, 2433–2437.
57. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2008, 10, 6630–6634.
58. H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676.
59. Y. Jiao, A. Du, M. Hankel, Z. Zhu, V. Rudolph and S. C. Smith, Chem. Commun., 2011, 47, 11843–11845.
60. M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593–2600.
61. D. Sebastiani and M. A. Parker, Symmetry, 2009, 1, 226–239.
62. A. Ivanovskii, Prog. Solid State Chem., 2013, 41, 1–19.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the studied molecules. See DOI: 10.1039/c5nr04370k

---