Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Laser directed writing of flat lenses on buckypaper†
Sunan
Deng
a,
Pavel
Penchev
a,
Jian
Liu
b,
Yongjing
Wang
a,
Kyle
Jiang
a,
Stefan
Dimov
a,
Zhichun
Zhang
c,
Yanju
Liu
c,
Jinsong
Leng
c and
Haider
Butt
*a
aNanotechnology Laboratory, School of Mechanical Engineering, University of Birmingham, Birmingham B15 2TT, UK. E-mail: h.butt@bham.ac.uk; Tel: +44 (0)121 4158623
bSchool of Manufacturing Science and Engineering, Sichuan University, Sichuan 610065, PR China
cCentre for Composite Materials and Structures, HIT Science Park, Harbin Institute of Technology, Harbin 150080, PR China
First published on 23rd June 2015
Abstract
Laser directed patterning of carbon nanotubes-based buckypaper for producing a diffractive optical device is presented here. Using a laser ablation method the buckypaper was patterned into a binary Fresnel zone plate lens. Computational modelling was performed which revealed excellent focusing performance of the lens for both visible and THz radiations. SEM and Raman measurements of the lens were studied to analyse the laser–material interaction. The focusing properties of the lens were characterized and a good agreement with the simulations was achieved. Hence, we exploited a new way to fabricate thin flat lens. The one-step fabrication process is economical, convenient and has great potential for industrial scale up.
Introduction
Since carbon nanotubes (CNTs; for single wall SWCNT; or multiwall MWCNT) were first discovered by Iijima in 1991,1 they have been the focus of a large amount of research due to their unique combination of exceptional electrical properties, extraordinary flexibility and high tensile strength.2 CNTs are stiff and strong, exhibiting an elastic modulus approaching 1 TPa and fracture stress as high as 100 GPa for individual MWCNTs;3 yielding a strength over 10-fold higher than any individual fibre. MWCNTs are typically metallic, while a SWCNT can be metallic or semiconducting depending on the chirality.4 In isolation the CNTs have limited uses; hence they are mostly produced in organized forms, such as vertically aligned forests,5 yarns and films,6 which show the promise of scaling up the properties of individual CNTs to realize new functionalities.Similarly, the macroscopic free standing CNT films, commonly referred to as buckypaper, are mats of entangled carbon nanotube ropes, formed via self-assembly of CNTs.7 Compared with the individual CNTs, this porous fibrous material has extended the excellent properties of CNTs from nanoscale to micro scale. Plenty of endeavours have been carried out to explore the potential applications of buckypaper; including artificial muscles,8 strain sensors9 and cold field emission cathodes,10 actuators,11 supercapacitors12 and so on.
The optical and AC electrical properties of various types of buckypaper have been studied in a wide frequency range from microwave to visible regime.13–20 It has been reported that vertical aligned CNT arrays were the darkest man-made material, with the capacity to absorb as high as 99.955% of incident visible light.21 Similar to vertical aligned CNT arrays, buckypaper can also be seen as an effective composite of carbon nanotubes and air and it also has high optical absorption. In the visible regime, buckypaper has been explored to work as a near-perfect absorber in cholesteric liquid crystal cells to develop a voltage-induced optical attenuator.20 In the THz frequency range buckypaper shows high shielding effects accompanied by a high dielectric constant close to that of normal metal.22 Hence buckypaper could be one of the alternative platforms for future THz optical and optoelectronic devices, replacing conventional metal films, which allow limited tunability in their optical properties. Due to its interesting optical properties, light weight, exceptionally high mechanical strength and conductivity, we explore to produce the buckypaper based flat lenses by direct laser writing process.
Flat lenses are vital technology for developing optical compact systems as such lenses have smaller volume and weight compared with traditional curved lenses. In addition, flat lenses can remove the distortions during imaging; these were previously corrected by utilising multi-lens systems, which are much more expensive and consume space. A Fresnel zone plate (FZP), which consists of a series of concentric rings alternating between transparent and opaque, offers a suitable way to develop flat lenses.23 FZP lenses are widely used in the optical industry and are key elements in systems like optical interconnects, beam focusing and integrated optics.24 Here we present a large area FZP lens fabricated by a direct laser writing process on buckypaper for the first time. Direct writing techniques enable computer controlled 2D and 3D pattern formation in a serial fashion. Compared with conventional techniques like lithography, stamping, directed self-assembly, or other patterning approaches that require masks or pre-existing patterns, the laser direct writing process provides high flexibility for arbitrary patterning via non-contact and maskless fabrication process, which is much cheaper and convenient.25 The study is of interest as it demonstrates the novel laser processing of buckypaper for producing a working diffractive optical device (FZP lens). The same method can also be applied for patterning buckypaper for other applications.
The buckypaper FZP lens was fabricated on silicon substrate with a radius of 2 mm and 16 Fresnel zones. A large area FZP lens has great potential to be used in photovoltaic and imaging applications.26 SEM and Raman measurements are taken to analyse CNTs after the laser process ablation. The working of the FZP lens and its performance in the visible and terahertz regimes was studied computationally. Experimental measurements were also performed to characterize the lens in the visible regime and good agreements with the simulations were achieved.
Simulations
The FZP lens is designed according to this equation: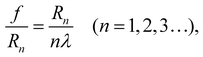 27–29 where Rn is the radius of the nth rings of a FZP lens; f is the focal length; and λ is the wavelength of incident light. In this work the central ring of the lens R1 is 500 μm, and nmax = 16.
27–29 where Rn is the radius of the nth rings of a FZP lens; f is the focal length; and λ is the wavelength of incident light. In this work the central ring of the lens R1 is 500 μm, and nmax = 16.
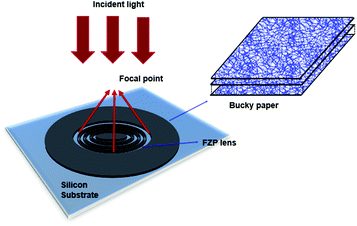
Fig. 1 shows the buckypaper FZP lens working under reflection mode, with the light incident from the top. Buckypaper has a laminar structure with networks of randomly oriented CNTs held together by van der Waals forces,12,30 as can be seen on the right of Fig. 1. In a format unlike individual CNTs, buckypaper has been developed to exploit and homogenize the excellent properties of CNTs. Given that CNTs are rolled-up graphene layers, the general features of CNT arrays are similar to those of bulk graphite.31–33 Also, rolled-up graphite was used to model the CNTs electron energy loss spectra (EELS)34–37 and good agreement has been achieved. We thus assume that buckypaper has electrical conductivity similar to the in-plane properties of bulk graphite in the visible regime.
The graphite in-plane dielectric function ε⊥ (ω) used for the simulation is from reference,38,39 which is consistent with continuity and Kramers–Kronig's requirements and can be fitted with a Drude–Lorenz model:
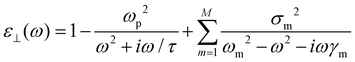 | (1) |
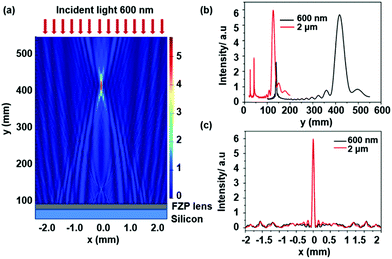
With the dielectric constants from eqn (1), the 2D focusing performances of the FZP lens were studied by a finite-difference time-domain (FDTD) method. Fig. 2(a) shows the E field distribution of 600 nm wavelength incidents light reflected from the buckypaper FZP lens, which were put on the XZ plane. The thickness of the lens and the substrate were set to 2.5 and 10 μm, respectively, to reduce the required simulation memory. A very clear focal point with high contrast could be seen. The black lines in Fig. 2(b) and (c) represent the intensity across the vertical and horizontal cross-section lines of the focal point. In Fig. 2(b), the black line peak near 150 mm was formed by second order diffraction from the lens; while the peak at 417.5 mm was caused by the first order diffraction. The depth of the focus (DOF) at the first order peak is 45.5 mm ≈ 7.58 × 104λin (λin is the incident light 600 nm), which means that the FZP lens has a very long DOF compared with the wavelength of the incident light. Long DOF lenses can provide a focusing range rather than a definite focal position, so they are critically important in optical coupling, optical imaging and optical interconnections.40
The lens performance was also studied with an incident light of 2 μm, shown as the red lines in Fig. 2(b) and (c). For 2 μm, the focal intensity is higher than that for a 600 nm light. The left two smaller peaks of the red line in Fig. 2(b) were generated by the third and second order diffractions of the lens. As for the DOF, the longer wavelength was accompanied by a shorter focus depth, with about 14.25 mm ≈ 7.1 × 103λin at first order peak for 2 μm incident light. The horizontal cross sectional lines at the focal point for an incident light of 600 nm and 2 μm are almost the same, with full wavelength at half maximum (FWHM) 0.06 mm, as demonstrated in Fig. 2(c).
In addition it is very important to realize modulation of THz wavelengths, which could be used in non-invasive quality control,41,42 security inspections43,44 and terahertz imaging systems.45,46 Therefore we studied the lens’ performance in a THz regime.
There are different models to describe the dielectric constant of buckypaper in THz.13,19,22As the properties of buckypaper are influenced by several factors, such as the synthesis methods and the properties of CNTs, we found a model which was quite similar to our case. The buckypaper we used was fabricated by a filtration method and composed of SWCNTs, with an effective thickness of 70 μm. We used the data from ref. 22 to carry out the simulations. What should be noticed is that this model may not be applied in other cases, like thin films within 1 μm or film synthesised via spin-spray method, due to the complexity of the buckypaper system.
The index and dielectric constants of free-standing 2.5 μm thick SWCNT films were derived from the amplitude and phase information extracted from the time-domain spectroscopy. The dielectric constants could be fitted by a classical Drude model for conductive metals:
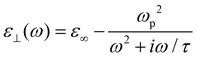 | (2) |
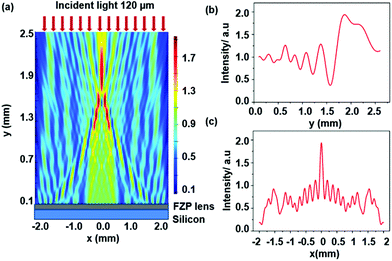
The incident light was 120 μm and the performance of the lens is illustrated in Fig. 3. The thickness of the buckypaper was still set to 2.5 μm, which was only 2.08% of the wavelength of the incident light. The DOF of the buckypaper FZP lens is almost 1 mm ≈ 8.3 λin at the focal length of 1.87 mm. The focal intensity is approximately 1.94 (a.u), much smaller than that of the visible (600 nm) and infrared (2 μm) light. The FWHM of the peak in Fig. 3(c) is 0.14 mm, comparable to the incident wavelength. Therefore the buckypaper FZP lens works very well in THz and it has the potential to be used in many THz applications.
Fabrication and characterization
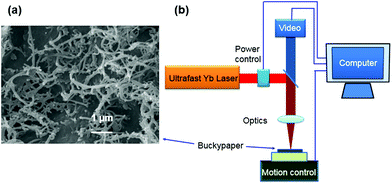
Buckypaper, with a thickness of 70 μm, was fabricated by multiple steps of SWCNT dispersion and suspension filtration,47 which is more efficient than the spin-coating technique.3 Due to the large aspect ratio, CNTs could stick together and form bundles easily under large van der Waal forces; therefore one of the major challenges of fabricating buckypaper is to separate the tubes without destroying them. Our dispersion method mainly consisted of two steps: (1) 1 g SWCNT mixed with 5 g Triton X-100 was dispersed by a three roller shear disperser (DS50, EXAKT) for 20 min; (2) The mixture in step (1) was dissolved in 5 L deionized water and dispersed by dynamic sonication using a high-power ultrasonic processor (Vibra-CellTM, Sonics) circulated twice. Then the homogeneous solution from the dispersion process was vacuum filtered onto a membrane with a pore size of 1 μm to form a SWCNT film. Finally, the as-prepared film was heated at 90 °C for 5 h and peeled from the filter membrane.An SEM image of the buckypaper is shown in Fig. 4(a), where the entangled mesh of CNTs can be clearly seen. Then buckypaper FZP lenses were fabricated by laser ablation.
Fig. 4(b) shows a simplified schematic of the multi-axes laser micro-machining system that was used to structure the lenses. An Yb-doped sub-Pico 5 W laser source from Amplitude Systems that operates at a central wavelength of 1030 nm with a pulse width of 310 fs and maximum repetitions rates of 500 kHz was used. The laser system also integrates a 100 mm telecentric focusing lens with a processing field of view of 35 mm by 35 mm. The laser ablation process can be monitored through a high resolution camera.
Table 1 gives the laser parameter settings which were used for the laser machining trials. Furthermore, in order to ensure a machining accuracy better than ±10 μm, a specialized software tool is used to minimize the dynamic effects of the beam delivery sub-system on machining results during the fabrication process.4
| Laser parameter | Units | Values |
|---|---|---|
| Power | W | 0.27 |
| Frequency | kHz | 60 |
| Scanning speed | m s−1 | 0.3 |
| Pulse duration | Fs | 310 |
| Beam diameter | μm | 30 |
| Hatch style | — | Random |
| Hatch pitch | μm | 5 |
| Layers | — | 7 |
Fig. 5(a) illustrates the whole FZP lens under SEM, while Fig. 5(b–f) show the magnified versions of different regions. Fig. 5 provides us with a further understanding of the CNT laser processing. In Fig. 5(a) and (b), there are some debris which appear on the edges of the ablated zones that are re-deposited CNTs during the laser irradiation process. The enlarged edge region containing the deposits is shown in Fig. 5(d). The edge of the buckypaper zone has a textured surface, with CNT bundled trimly (Fig. 5(e)); which is very different from the ablated area shown in Fig. 5(f).
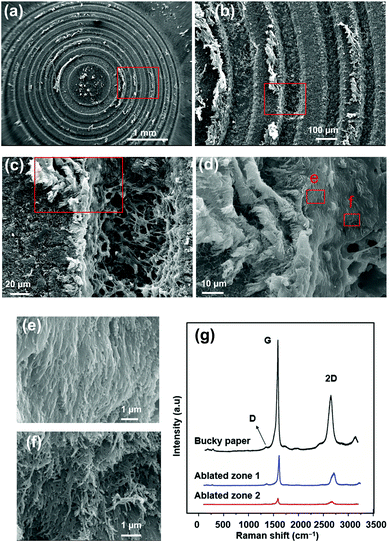 | ||
| Fig. 5 SEM pictures of buckypaper FZP lens. (a) Single buckypaper FZP lens. (b) Magnified version of red square in (a). (c) Magnified version of red square in (b). (d) Magnified version of red square in (c). (e) and (f) correspond to the areas labelled e and f in (d). (g) Raman spectra of buckypaper (black line), ablated zone 1 (blue line, area in Fig. 5(f)) and ablated zone 2 (red line, porous area in Fig. 5(c)). | ||
The area shown in Fig. 5(f) is ablated zone 1, which Raman spectra is shown as the blue curve in Fig. 5(g). The ablated area shown in Fig. 5(c) has a porous rough surface, associated with the photoexcitation phenomena and competing localized and delocalized relaxation processes to dissipate the absorbed energy into the silicon substrate. When the ultra-short pulse from the laser hit silicon, the electrons of Silicon will absorb photons and be excited to high energy level. Following photoexcitation, the excited system begins to evolve on the surface determined by the competition between localized excitations – such as trapping at defects, or self-trapping by lattice distortion – and delocalized mechanisms of energy loss, such as electron-phonon scattering.9,10 During this process, the absorbed energy was redistributed through electron–phonon interaction, resulting in high temperature, which may exceed the silicon melting point. The porous surface will be formed when the molten layer cools down quickly.11
It is expected that there are still some CNTs left in the porous area, which is named as the ablated zone 2. This can be confirmed by CNT Raman characteristic peaks (red line) in Fig. 5(g). As CNT Raman characteristic peaks are present on the surface most likely this is due to different ablation thresholds of CNTs and Si that lead to surface porosity. Such surface morphology can result in ultrafast laser processing of multi-phase materials. As the paper reports a feasibility study, an in-depth investigation of laser–material interactions when processing buckypaper is outside its scope.
The decreased Raman intensity from buckypaper to ablated zone 2 implies a decreased quantity of CNTs due to the laser ablation. The D peak at about 1330 cm−1 stems from a structural defect of the graphite-like material, while the G peak near 1600 cm−1 is because of plane vibration in the sp2 carbon materials.48 Therefore, the ratio of the intensities of G to D peaks (IG/ID) is usually used to evaluate the quality in graphitic carbon materials. By calculation, it is noticed that IG/ID of buckypaper is 18.18, much larger than that of ablated zones 1 and 2 which are 14.32 and 10.18 respectively. The results indicate that the higher amount of defects in the CNTs was formed during the laser processing. The 2D peak at about 2660 cm−1 is a second order peak of the D mode; and the intensity I2D/IG is often used to estimate the thickness of graphene layers. Here the intensity ratio I2D/IG of buckypaper, ablated zone 1 and 2 are decreasing gradually, with 0.494, 0.465 and 0.412 respectively. Thus is can be deduced that CNTS behave much more like graphite after dissipating the absorbed energy into the silicon during the photoexcitation process.
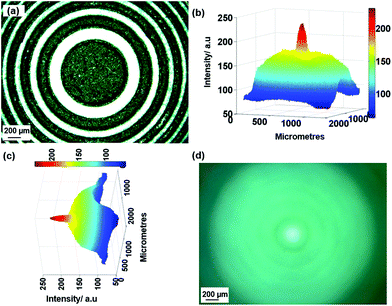
The fabricated buckypaper FZP lens was characterised under an optical microscope (Alicona infinite) at a magnification of ×5. Fig. 6(a) shows the FZP lens under the microscope, with a great deal of contrast between the CNT zones (black) and the ablated zones (white). A high degree of reflection from the ablated Fresnel zones shows that most of the CNTs have been removed by laser ablation. Fig. 6(d) shows that light from the ablated zones is focused into a bright spot in the middle with a focal length of 4.63 mm, which corresponds to the high order diffraction effect. Due to detection limitation, it was difficult to measure the first order focal point, which will be in the range of 357 mm to 625 mm for visible incident light (400–700 nm). Fig. 6(b) and (c) are 3D intensity distribution of Fig. 6(d). Therefore the FZP lens works very well under the visible regime and the results are consistent with the simulations. Also, the efficiency of FZP lens will be higher with higher reflection contrast between the transparent zones and the opaque zones. Thus if the roughness of the silicon surface could be reduced during laser processing, better lens performance can be achieved.
Conclusion
In this work, we have demonstrated novel laser processing of CNT based buckypaper. Laser ablation was utilised for patterning the buckypaper into a Fresnel zone plate which displays a high degree of contrast focusing and good DOF. Material characterisation and the tested focusing performance of the lens were consistent with the simulations. The results show that this laser processing technique can also be used for pattering other diffractive, holographic and electrical devices which rely on buckypaper and related materials.Acknowledgements
H. Butt would like to thank The Leverhulme Trust for the research funding.References
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS PubMed.
- R. H. Baughman, A. A. Zakhidov and W. A. de Heer, Science, 2002, 297, 787–792 CrossRef CAS PubMed.
- J. H. Yim, Y. S. Kim, K. H. Koh and S. Lee, J. Vac. Sci. Technol., B, 2008, 26, 851–855 CAS.
- D. S. Penchev, D. Bhaduri, S. L. Soo and B. Crickboom, submitted to ImechE Part B paper: June 2014, 2014.
- Y. Montelongo, B. Chen, H. Butt, J. Robertson and T. D. Wilkinson, Appl. Phys. Lett., 2013, 103, 111104 CrossRef PubMed.
- A. A. Khan, G. D. M. Dabera, H. Butt, M. M. Qasim, G. A. Amaratunga, S. R. P. Silva and T. D. Wilkinson, Nanoscale, 2015, 7, 330–336 RSC.
- E. Lidorikis and A. C. Ferrari, ACS Nano, 2009, 3, 1238–1248 CrossRef CAS PubMed.
- A. Ugawa, A. G. Rinzler and D. Tanner, Phys. Rev. B: Condens. Matter, 1999, 60, R11305 CrossRef CAS.
- R. F. Haglund, Exp. Methods Phys. Sci., 1997, 30, 32–39 Search PubMed.
- A. Piqué and D. B. Chrisey, Direct-write technologies for rapid prototyping applications: sensors, electronics, and integrated power sources, Academic Press, 2001 Search PubMed.
- B. R. Tull, PhD thesis in Applied Physics, Harvard University, 2007, pp. 6–8.
- D. Jack, C. Yeh, Z. Liang, S. Li, J. Park and J. Fielding, Nanotechnology, 2010, 21, 195703 CrossRef CAS PubMed.
- E. Dadrasnia, S. Puthukodan and H. Lamela, J. Nanophotonics, 2014, 8, 083099–083099 CrossRef PubMed.
- O. Hilt, H. B. Brom and M. Ahlskog, Phys. Rev. B: Condens. Matter, 2000, 61, R5129–R5132 CrossRef CAS.
- N. Akima, Y. Iwasa, S. Brown, A. M. Barbour, J. Cao, J. L. Musfeldt, H. Matsui, N. Toyota, M. Shiraishi, H. Shimoda and O. Zhou, Adv. Mater., 2006, 18, 1166–1169 CrossRef CAS PubMed.
- H. Xu, S. M. Anlage, L. Hu and G. Gruner, Appl. Phys. Lett., 2007, 90 Search PubMed , 183119.
- T. Kampfrath, K. von Volkmann, C. Aguirre, P. Desjardins, R. Martel, M. Krenz, C. Frischkorn, M. Wolf and L. Perfetti, Phys. Rev. Lett., 2008, 101, 267403 CrossRef CAS.
- Q. Zhang, E. H. Hároz, Z. Jin, L. Ren, X. Wang, R. S. Arvidson, A. Lüttge and J. Kono, Nano Lett., 2013, 13, 5991–5996 CrossRef CAS PubMed.
- T.-I. Jeon, K.-J. Kim, C. Kang, S.-J. Oh, J.-H. Son, K. H. An, D. J. Bae and Y. H. Lee, Appl. Phys. Lett., 2002, 80, 3403–3405 CrossRef CAS PubMed.
- H.-K. Ma, P.-C. Chien, M.-C. Tsai, H.-Y. Miao, J.-H. Liu and C.-Y. Huang, Opt. Mater. Exp., 2014, 4, 719–724 CrossRef.
- Z.-P. Yang, L. Ci, J. A. Bur, S.-Y. Lin and P. M. Ajayan, Nano Lett., 2008, 8, 446–451 CrossRef CAS PubMed.
- J. Hong, D. J. Park, J. H. Yim, J. Park, J.-Y. Park, S. Lee and Y. Ahn, J. Phys. Chem. Lett., 2013, 4, 3950–3957 CrossRef CAS.
- K. Rastani, A. Marrakchi, S. F. Habiby, W. M. Hubbard, H. Gilchrist and R. E. Nahory, Appl. Opt., 1991, 30, 1347–1354 CrossRef CAS PubMed.
- H. Butt, R. Rajesekharan, Q. Dai, S. Sarfraz, R. V. Kumar, G. A. Amaratunga and T. D. Wilkinson, Appl. Phys. Lett., 2012, 101, 243116 CrossRef PubMed.
- W. Xiong, Y. S. Zhou, W. J. Hou, L. J. Jiang, Y. Gao, L. S. Fan, L. Jiang, J. F. Silvain and Y. F. Lu, Sci. Rep., 2014, 4 Search PubMed.
- W. T. Xie, Y. J. Dai, R. Z. Wang and K. Sumathy, Renewable Sustainable Energy Rev., 2011, 15, 2588–2606 CrossRef PubMed.
- R. Ranjith, H. Butt, T. Wilkinson and G. Amaratunga, Adv. Mater., 2012, 24, OP170–OP173 Search PubMed.
- S. Deng, A. K. Yetisen, K. Jiang and H. Butt, RSC Adv., 2014, 4, 30050–30058 RSC.
- X.-T. Kong, A. A. Khan, P. R. Kidambi, S. Deng, A. K. Yetisen, B. Dlubak, P. Hiralal, Y. Montelongo, J. Bowen and S. Xavier, ACS Photon., 2015, 2(2), 200–207 CrossRef CAS.
- S. Roy, V. Jain, R. Bajpai, P. Ghosh, A. Pente, B. Singh and D. Misra, J. Phys. Chem. C, 2012, 116, 19025–19031 CAS.
- Y. Murakami, E. Einarsson, T. Edamura and S. Maruyama, Phys. Rev. Lett., 2005, 94, 087402 CrossRef.
- M. F. Lin, F. L. Shyu and R. B. Chen, Phys. Rev. B: Condens. Matter, 2000, 61, 14114–14118 CrossRef CAS.
- H. Pan, Y. Feng and J. Lin, Phys. Rev. B: Condens. Matter, 2005, 72, 085415 CrossRef.
- A. Seepujak, U. Bangert, A. Harvey, P. Costa and M. Green, Phys. Rev. B: Condens. Matter, 2006, 74, 075402 CrossRef.
- O. Stéphan, D. Taverna, M. Kociak, K. Suenaga, L. Henrard and C. Colliex, Phys. Rev. B: Condens. Matter, 2002, 66, 155422 CrossRef.
- A. Rivacoba and F. J. García de Abajo, Phys. Rev. B: Condens. Matter, 2003, 67, 085414 CrossRef.
- M. Kociak, L. Henrard, O. Stéphan, K. Suenaga and C. Colliex, Phys. Rev. B: Condens. Matter, 2000, 61, 13936–13944 CrossRef CAS.
- H. Butt, Q. Dai, R. Rajesekharan, T. D. Wilkinson and G. A. Amaratunga, ACS Nano, 2011, 5, 9138–9143 CrossRef CAS PubMed.
- T. D. W. H. Butt and G. A. J. Amaratunga, Prog. Electromagn. Res., 2012, M 22, 1–12 CrossRef.
- X.-Y. Jiang, J.-S. Ye, J.-W. He, X.-K. Wang, D. Hu, S.-F. Feng, Q. Kan and Y. Zhang, Opt. Express, 2013, 21, 30030–30038 CrossRef PubMed.
- H. Hoshina, Y. Sasaki, A. Hayashi, C. Otani and K. Kawase, Appl. Spectrosc., 2009, 63, 81–86 CrossRef CAS PubMed.
- F. Rutz, M. Koch, S. Khare, M. Moneke, H. Richter and U. Ewert, Int. J. Infrared Millimeter Waves, 2006, 27, 547–556 CrossRef CAS.
- K. Yamamoto, M. Yamaguchi, F. Miyamaru, M. Tani, M. Hangyo, T. Ikeda, A. Matsushita, K. Koide, M. Tatsuno and Y. Minami, Jpn. J. Appl. Phys., 2004, 43, L414 CrossRef CAS.
- M. C. Kemp, P. Taday, B. E. Cole, J. Cluff, A. J. Fitzgerald and W. R. Tribe, International Society for Optics and Photonics, 2003, pp. 44–52 Search PubMed.
- K. J. Siebert, T. Löffler, H. Quast, M. Thomson, T. Bauer, R. Leonhardt, S. Czasch and H. G. Roskos, Phys. Med. Biol., 2002, 47, 3743 CrossRef.
- A. W. Lee and Q. Hu, Opt. Lett., 2005, 30, 2563–2565 CrossRef.
- H. Chu, Z. Zhang, Y. Liu and J. Leng, Carbon, 2014, 66, 154–163 CrossRef CAS PubMed.
- J. Li, X. Cheng, J. Sun, C. Brand, A. Shashurin, M. Reeves and M. Keidar, J. Appl. Phys., 2014, 115, 164301 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr02481a |
| This journal is © The Royal Society of Chemistry 2015 |