Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Preparing a pseudo-solid by the reinforcement of a polydentate thioether using silver nanoparticles†
Holger
Pletsch
,
Andreas
Greiner
and
Seema
Agarwal
*
Faculty of Biology, Chemistry and Earth Sciences, Macromolecular Chemistry II and Bayreuth Center for Colloids and Interfaces, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany. E-mail: agarwal@uni-bayreuth.de
First published on 15th December 2014
Abstract
The design of networks from polymers and noble metal nanoparticles requires thorough control over topological polymer–particle arrangements. This study explores the interaction between a linear polydentate poly(propylene sulfide) (PPrS) ligand and silver nanoparticles (AgNPs) with an aim to study its effect on mechanical and viscoelastic properties. Very low amounts (0.30 vol%) of silver nanoparticles lead to significant mechanical reinforcement of PPrS, yielding viscoelastic properties of an unfastened network with solid-like elastic responses on mechanical stimulation. The materials are made by ring-opening anionic polymerization of propylene sulfide to yield high molar mass PPrS with a total of 593 thioether functionalities per chain, followed by a simple in situ “grafting to” method to homogeneously incorporate AgNPs into the polymer matrix. From investigations on the chain dynamics using dynamic rheology it is concluded that well-dispersed AgNPs impose additional topological constraints on the polymer chains. Calculations of the statistical interparticle distances support a tele-bridging polymer–particle arrangement.
Introduction
Polymer-grafted metal nanoparticles have been subjected to a plethora of studies, including but not limited to those with a focus on nanomaterials,1–5 on interaction with biological systems6–8 and on plasmonic applications.9–12 Most decisive considerations for the design of such symbiotic nanocomposites not only include the right choice of polymer type, but also of a suitable anchor group as well as its position and quantity in the polymer chain. Despite being the “gold standard” anchor group for noble metal nanoparticles such as Ag or Au for good reasons, thiols can also be a handicap if used as anchor groups in polymers. First, thiols may only be structurally located at the termini of polymer main or side chains and second, their considerable sensitivity towards photodegradation by UV light13,14 and oxidation15 impedes real-world applications. Thioether groups overcome these drawbacks and have been identified to be suitable for stabilizing noble metal nanoparticles both in experiment16,17 and in simulation.18 While oligomeric19,20 and dendritic21,22 thioether ligands were shown to wrap around noble metal nanoparticles, herein our aim is to use linear, high molar mass polydentate thioethers in order to design a polymer–particle network microstructure in which metal nanoparticles act as structural reinforcing sites. Therefore, we present for the first time poly(propylene sulfide) (PPrS) as a liquid polydentate thioether ligand for silver nanoparticles (AgNPs).Although metal nanoparticles are well known for their capacity to contribute to chemical, physical and also biological properties in nanocomposite materials, their potential as cross-linking and reinforcing agents is still largely unexplored. Only recently, thermally processable elastomers have been designed from polymer–particle networks in which bidentate (telechelic) α,ω-dithiol oligomers were grafted to AgNPs.23,24 In this context, Zhang et al. had suggested a polymer–particle network microstructure from linear, polydentate poly(ethylene oxide) with high molar masses (ranging from 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 292
000 to 292![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) and silica nanoparticles.25 However, the authors reported that homogeneous dispersions of silica particles in the polymer matrix well below the percolation threshold were subjected to thermal instability, leading to particle flocculation and therefore, to a reduced specific surface area. Improved colloidal stability of silica nanoparticle–polymer networks was provided via covalent polymer–particle bonding, for instance induced by additional silane coupling agents as shown for the preparation of hydrogel networks.26 It is further known that by exceeding the percolation threshold, liquid polymers such as non-cross-linked 1,4-polybutadiene27 and poly(dimethyl siloxane)28 undergo reinforcement if charged with silica nanoparticles at high filling rates, leading to continuous particle–particle networks. In the present work we will show that already low AgNP filling rates below the percolation threshold are sufficient to trigger significant reinforcement of PPrS, accompanied by high colloidal stability.
000 g mol−1) and silica nanoparticles.25 However, the authors reported that homogeneous dispersions of silica particles in the polymer matrix well below the percolation threshold were subjected to thermal instability, leading to particle flocculation and therefore, to a reduced specific surface area. Improved colloidal stability of silica nanoparticle–polymer networks was provided via covalent polymer–particle bonding, for instance induced by additional silane coupling agents as shown for the preparation of hydrogel networks.26 It is further known that by exceeding the percolation threshold, liquid polymers such as non-cross-linked 1,4-polybutadiene27 and poly(dimethyl siloxane)28 undergo reinforcement if charged with silica nanoparticles at high filling rates, leading to continuous particle–particle networks. In the present work we will show that already low AgNP filling rates below the percolation threshold are sufficient to trigger significant reinforcement of PPrS, accompanied by high colloidal stability.
Results
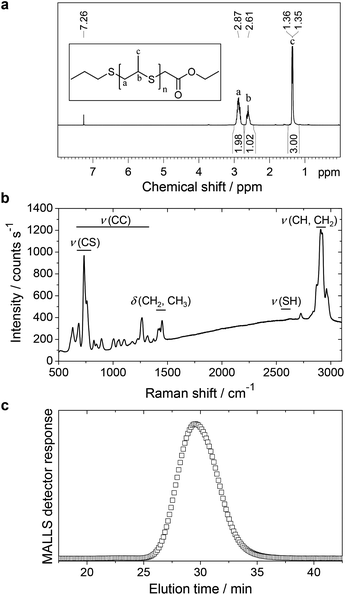
Linear PPrS with high purity (Fig. 1a) was obtained as a viscous, colorless liquid via ring-opening anionic polymerization of propylene sulfide along the lines of a previously published procedure.29 Subsequent end-capping using ethyl bromoacetate successfully suppressed the formation of thiol end groups as seen in the Raman spectrum (Fig. 1b).13 A total of 593 thioether units per polymer chain was calculated from Mn = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, determined by GPC with a multi angle laser light scattering detector (MALLS) (Fig. 1c).
000 g mol−1, determined by GPC with a multi angle laser light scattering detector (MALLS) (Fig. 1c).
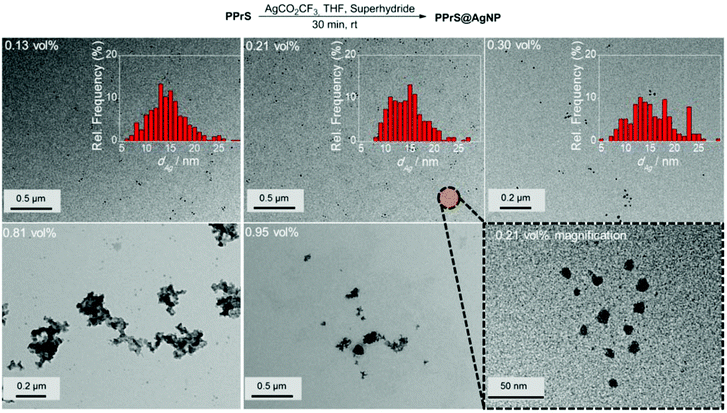
Grafting of PPrS as a polydentate ligand to AgNP was performed using an in situ method in which different feed amounts of THF-soluble AgCO2CF3 were employed as the AgNP precursor and Superhydride® as the reducing agent to yield AgNP filling rates ϕ ranging from 0.13 to 0.95 vol%. The resulting materials are designated as for example PPrS@AgNP0.13 with subscript 0.13 representing ϕ in vol% (Table 1).
| ϕ [vol%] |
d
AgNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [nm] a [nm] |
T
g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b [K] b [K] |
Material appearance |
|---|---|---|---|
| a The average AgNP diameters dAg were calculated from TEM micrographs by measuring at least 150 particles for each sample. b Obtained from DSC measurements. | |||
| 0 | — | 235 | Viscous liquid |
| 0.13 | 14.4 ± 3.6 | 235 | Very soft material |
| 0.21 | 14.3 ± 4.0 | 234 | Soft material |
| 0.30 | 14.9 ± 4.6 | 233 | Soft material |
| 0.81 | Aggregation | 234 | Very soft material |
| 0.95 | Aggregation | 233 | Very soft material |
According to TEM investigations, AgNPs are successfully stabilized by PPrS up to a filling rate of ϕ = 0.30 vol%, being well-dispersed with no signs of particle aggregation (Fig. 2). The presence of a regular AgNP superlattice is not observed which leads us to the conclusion that the nanocomposite is a mixture of AgNP-grafted PPrS and excess non-grafted PPrS chains. Localized surface plasmon resonance responses characteristic for AgNP were observed in absorption spectroscopy (please find details in the ESI;† Fig. S1). The colloidal stability of PPrS@AgNP was maintained even under demanding conditions such as during hot pressing at 353 K and 300 bar pressure or during long-term exposure to high temperatures (7 h at 343 K) as TEM micrographs did not unfold changes in particle sizes and morphology. The high particle stability is assumed to be due to the virtually ubiquitous presence of anchor groups. Please find information about further experiments on thermal stability in the ESI† (Fig. S2).
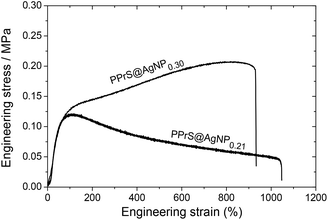
In particular, samples PPrS@AgNP0.21 and PPrS@AgNP0.30 appear as soft materials with high extensibility, showing ultimate elongations of 906 ± 77% and 1011 ± 142%, respectively, in linear uniaxial tensile testing (Fig. 3). With tensile strengths of 106 ± 10 Pa for PPrS@AgNP0.21 compared to 212 ± 18 Pa for PPrS@AgNP0.30 we observed a strong impact of the AgNP filling rate on the material properties. The degree of reinforcement is quantified using dynamic rheology at both 298 K and at elevated temperatures. Measurements under constant conditions (T = 298 K, angular frequency ω = 1.0 rad s−1) were performed, followed by the determination of the loss factors tan(δ) = G′′/G′ (shear loss modulus/shear storage modulus) as a function of ϕ (Fig. 4a) in order to quantify the impact of AgNPs on the viscoelastic properties. Through grafting with AgNPs, the loss factors were heavily decreased, yet ϕ was found to be a variable of major importance. A minimum of tan(δ) = 0.38 ± 0.003 is identified for ϕ = 0.30 vol% which represents the most effective reinforcement scenario within this sample set as here the elastic portions preponderate to a large extent. In context, reinforcement of non-cross-linked liquid polymers has also been accomplished by using carbon black30 and spherical silica nanoparticles;25,31 yet much higher filling rates were employed in these studies. At filling rates of ϕ = 0.81 and 0.95 vol%, AgNP aggregation impairs polymer–particle interactions leading to a slight increase in tan(δ). Temperature-dependent measurements at constant ω = 1.0 rad s−1 show stepless softening for all samples, resulting in less elastic behavior at elevated temperatures (Fig. 4b). The degree of softening can be derived from the slopes of the temperature-dependent loss factor curves with steep ascending slopes representing a high affinity towards temperature-induced softening. By addition of AgNP, slopes are significantly damped down; therefore softening of PPrS@AgNP is suppressed in comparison to the neat polymer.
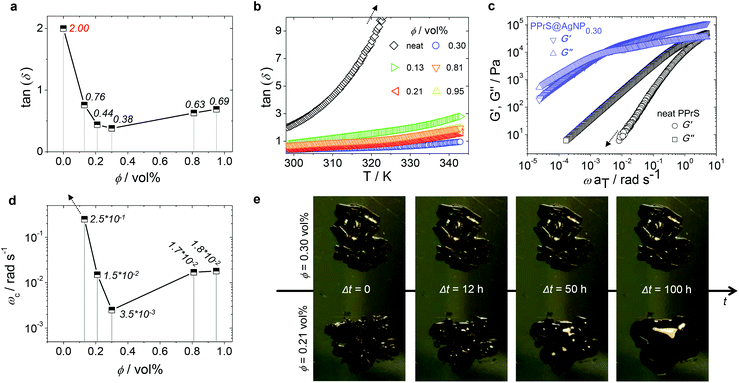 | ||
| Fig. 4 ϕ- and T-dependent viscoelastic behavior. (a) Plot of the loss factors tan(δ) as a function of ϕ at T = 298 K and ω = 1 rad s−1 for both neat PPrS and PPrS@AgNP samples (italic typed values represent the exact loss factor of the corresponding sample). Elasticity increased significantly after AgNP addition, reaching extreme value at ϕ = 0.30 vol% in this sample set. Standard deviations are below 1% for all samples and therefore, not cited. The line serves as a guide to the eye. (b) Loss factors tan(δ) of neat PPrS and PPrS@AgNP samples as a function of temperature (heating rate ΔT = 0.5 K min−1; ω = 1.0 rad s−1). The softening degree according to the slopes is damped down for PPrS@AgNP samples in comparison to neat PPrS. (c) G′ and G′′ master curves of neat PPrS and PPrS@AgNP0.30 from frequency–temperature superposition (FTS). For clarity, master curves of the other samples are not shown here, but can be found in the ESI† (Fig. S3). The G′ trace of neat PPrS is cropped as the rheometer detection limit is reached. (d) G′–G′′ crossover frequency ωc as a function of ϕ (italic typed values represent the exact crossover frequency of the corresponding sample). The trend shown here is comparable to the loss factors depicted in part (a) of this figure with PPrS@AgNP0.30 exhibiting the most increased relaxation times within the sample set. The line serves as a guide to the eye. (e) Demonstration of flow behavior at T = 293 K without external stimuli. PPrS@AgNP0.21 exhibits liquid flow up to formation of a droplet, whereupon PPrS@AgNP0.30 remains form-stable in the same time range. | ||
In the following, we probe the chain dynamics of our samples in order to approach the origin for reinforcement. From DSC measurements it is known that the segmental chain dynamics are not affected by AgNP addition (cf. Table 1). Insight into the frequency-dependent viscoelastic behaviour was provided via assumption of frequency–temperature superposition (FTS) for frequency sweep experiments in a dynamic rheology setup at T = 198–343 K in ΔT = 5 K steps, yielding G′ and G′′ master curves (those of neat PPrS and PPrS@AgNP0.30 are presented in Fig. 4c; please find those of the other samples in the ESI;† Fig. S3). We find liquid-like viscoelastic properties for the nanocomposites with G′′ > G′ at low frequencies; however, we also observe clear alterations concerning the terminal relaxation time as a function of ϕ. Most notably, the PPrS@AgNP G′–G′′ crossover frequencies ωc significantly shift to lower frequencies compared to neat PPrS. Following the same trend as observed during evaluation of tan(δ) from constant measurement conditions (cf. Fig. 4a), PPrS@AgNP0.30 is affected most intensively within this sample set with ωc being shifted more than three orders of magnitude down to 3.5 × 10−3 rad s−1 compared to neat PPrS holding ωc > 5 rad s−1 (Fig. 4d). Though longer relaxation time processes are not completely eliminated, the strong shift of ωc causes PPrS@AgNP0.30 to maintain form-stability over five days (Fig. 4e) and is therefore regarded as a pseudo-solid.
Discussion
A relaxation enhancement caused by decelerated polymer dynamics at low shear frequencies and simultaneous retention of segmental dynamics as observed for the nanocomposites with respect to the neat system herein (cf. Fig. 4c) is evidence for additional topological constraints imposed by well-dispersed nanoparticles which have been simulated previously under similar conditions.32 It is a challenge to disclose the actual topological polymer–particle arrangement within the nanocomposite. One possible approach is to calculate the statistically averaged interparticle distance Λ by assuming a homogeneous particle packing on a cubic lattice along the lines of previous considerations on other polymer–particle systems.25,33 Assuming attractive energetic polymer–particle interaction such as that simulated for other similar systems18 and therefore, a closed polymer ligand shell around the particle core, we first calculate the polymer shell thickness according to eqn (1).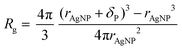 | (1) |
Taking the polymer shell thickness into consideration, the effective particle volume fraction ϕeff is then calculated from eqn (2).
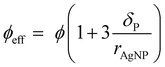 | (2) |
Finally, the AgNP interparticle distances Λ are calculated according to eqn (3).
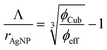 | (3) |
In a non-dynamic approach where the chain diffusion and particle-induced chain conformation changes such as contraction through attractive polymer–particle interactions are neglected, conclusions can be drawn on the dominating topological polymer–particle arrangement as a function of the interparticle gap size:
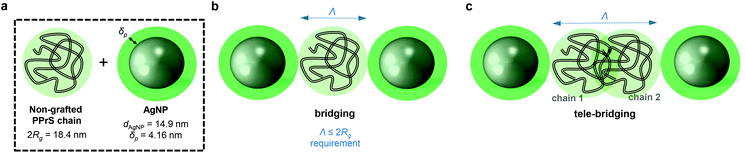
(1) if Λ approaches 0, a superlattice layout without interjacent non-grafted polymer chains would be the consequence. (2) A scenario where one non-grafted polymer chain is confined by two particles is referred to as bridging (Scheme 1b) and has been identified as accountable for inducing a polymer–particle network and therefore, mechanical reinforcement in previous simulation experiments.34,35 Bridging only comes into effect if the interparticle distance Λ is small relative to the polymer dimensions; i.e. Λ ≤ 2Rg. (3) For larger interparticle distances, exceeding 2Rg, long range polymer–particle interactions through physical polymer–polymer junctions (entanglements) between at least two polymer chains come into effect (Scheme 1c). This scenario is also referred to as “tele-bridging” and has been predicted in computer simulations.36
For PPrS@AgNPs with ϕ = 0.30, 0.21, 0.13, polymer shell thicknesses δP = 4.16, 4.14, 4.15 nm are estimated from Rg = 9.2 nm (determined by GPC with a multi angle laser light scattering detector) and rAgNP = 7.45, 7.15, 7.20 nm, yielding Λ = 24.6, 27.2, 33.7 nm, respectively. Thus, Λ approaches 2Rg with increasing ϕ; still Λ > 2Rg holds for the non-aggregated nanocomposites. In turn, our PPrS@AgNP materials do not meet the Λ ≤ 2Rg requirement for bridging nanoparticles over a single polymer chain. However, Λ ≤ 4Rg applies for our nanocomposites, guaranteeing overlap of two (or more) different polymer chains in between the interparticle gap. Consequently, a tele-bridging scenario becomes plausible for our system. The resulting topological constraints and therefore, the levels of confinement densify with decreasing Λ (i.e. with increasing ϕ) and trap the chains’ primitive paths, yielding rather unfastened than permanent networks which explain our experimental results well. We believe that in particular field cycling 1H-NMR spectroscopy37 may provide a promising spectroscopic insight into such particle- and entanglement-mediated networks in future studies.
Experimental
Materials
Tetrahydrofuran was purified by consecutive drying over CaH2 and potassium with subsequent distillation under nitrogen atmosphere. MeOH was purified by distillation. Propylene sulfide (Acros, 98%) was dried over CaH2, distilled and stored at 5 °C under argon. Silver trifluoroacetate (98%, Acros) was purified by recrystallization from Et2O. Superhydride® (1.0 mol L−1 in THF, Aldrich), S-n-propyl thioacetate (Alfa Aesar, 98%), tri-n-butyl phosphine (Acros, 95%), NaOMe (Fluka, >97%) and ethyl bromoacetate (Aldrich, 98%) were used as received.Methods
The number-average molecular weights (Mn) and the number-average radius of gyration Rg of the neat polymer were determined by gel permeation chromatography (GPC) in THF at 26 °C using an Agilent 1200 series system equipped with a PSS-SDV (10 μm) 50 × 8 mm2 pre-column, three linear PSS-SDV (10 μm) 300 × 8 mm2 columns at a flow rate of 0.8 mL min−1 (sample concentration 2 mg mL−1) and a Wyatt Dawn Heleos multi angle laser light scattering (MALLS) detector. dn/dc was determined with a PSS DnDc-2010 λ620 device. dn/dc of PPrS was 0.168 mL g−1.A confocal microscope (LabRAM Division, HORIBA Jobin Yvon) equipped with a Olympus 10×, NA = 0.25 lens, a linear-polarized HeNe laser (633 nm) and a Peltier-cooled CCD camera (−70 °C, Synapse) detector situated behind an 1800 grooves mm−1 grating spectrometer were used for Raman measurements. Spectra were accumulated from 10 measurements at three positions more than 300 μm apart from each other.
A Mettler thermal analyzer 821 DSC was utilized for DSC scans. Temperature and enthalpy calibrations were carried out with indium and zinc standards and tested with n-octane as a reference. 5 ± 2 mg of the samples were analyzed under nitrogen atmosphere (flow rate 80 mL min−1) at a heating rate of 10 K min−1. The glass transition temperature (Tg) was taken as the inflection point of the observed shift in the baseline of the second heating cycle.
The 1H-NMR (300.13 MHz) spectrum was recorded on a Bruker Avance 300 A spectrometer using CDCl3 as a solvent with a concentration of 100 g L−1. The signals were calibrated to the solvent signal.
TEM measurements were done in a Zeiss 922 OMEGA EFTEM at a voltage of 200 kV. Zero-loss filtered images were recorded using a bottom mounted Ultrascan 1000 (Gatan) CCD camera system. Gatan Digital Micrograph 3.9 for GMS 1.4 software was used for image acquisition. Samples were prepared from solution by drop-casting on a Quantifoil 300 mesh copper grid with carbon coating. For AgNPs mean diameter determination, ImageJ (version 1.44p) of the National Institute of Health, USA, was used.
A Malvern Instruments Bohlin Gemini HR Nano device with a 2 cm stainless steel plate–plate setup in shear strain-controlled mode was used for dynamic rheology. Solid samples were molded into discs with 2 cm diameter. Liquid samples were distributed between the plates without previous molding. The plate–plate gap was kept constant at 1 mm throughout all measurements. The linear viscoelastic (LVE) ranges of the samples were determined by performing strain sweeps with deformations between 0.01 and 10% and constant angular frequencies of 0.01, 0.1, 1.0 and 5.0 Hz at 298 and 343 K. Constant dynamic rheology was carried out at 1.0% strain, a frequency of 1.0 Hz and a temperature of 298 K. Temperature-ramp experiments were carried out between 298 and 343 K with a constant strain of 1.0%, a constant frequency of 1.0 Hz and a constant heating rate of 0.5 K min−1. Frequency sweep experiments were performed with constant temperatures between 298 and 343 K in 5 K steps, constant strain of 1.0% and a frequency range between 0.01 and 5.0 Hz. The master curves were generated by frequency–temperature superposition (FTS) with the frequency curve measured at 298 K being the reference temperature.
Linear uniaxial tensile testing was performed on a Zwick Roell Z0.5 device equipped with a Zwick Roell KAF-TC 1 kN load sensor at a strain rate of 200 mm min−1. Zwick Roell testXpert II V 3.0 software was used for acquisition. The dog bone specimens were pressed with a hand-operated Ray-Ran cutting press from homogeneous films with a thickness of 1 mm. The exact thicknesses of the specimens were determined by a Mitutoyo micrometer screw. Grip-to-grip separation was 10 mm and the bar width was 2 mm. Upon loading, a slack was observed which was deducted in elongation at break determination. The tensile strengths were identified at the stress maxima of the curves. Values represent the average of seven measurements and refer to the engineering curves.
Preparation of PPrS
A previously reported procedure29 was modified to synthesize PPrS. 1.37 mL of an S-n-propyl thioacetate stock solution in THF (c = 165 mmol L−1) and 0.16 mL (631 μmol) tri-n-butyl phosphine were added into 100 mL THF with subsequent degassing via Ar-bubbling. 0.27 mL of a degassed NaOMe solution in MeOH (c = 0.5 mol L−1) was added and stirred for 15 min. 12.0 mL (153 mmol) of degassed propylene sulfide was added quickly. After stirring for 70 min at room temperature 0.56 mL (5.04 mmol) of degassed ethyl bromoacetate was added and stirred for 2 h at room temperature. After precipitation in MeOH the supernatant was decanted and the polymer was dried in vacuo. A transparent, colorless viscous liquid was obtained.
M
n = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Mw = 64
000, Mw = 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200, Rg = 9.2 nm. Polymerization degree was calculated from GPC-MALLS: 593.
200, Rg = 9.2 nm. Polymerization degree was calculated from GPC-MALLS: 593.
Preparation of PPrS@AgNP0.21
1.153 g (58.8 μmol) PPrS was dissolved in 30 mL THF and charged with 49.0 mg (222 μmol) AgCO2CF3. 0.9 mL of a Superhydride® solution in THF (c = 1 mol L−1) was added slowly at room temperature during vigorous stirring. After 30 min the reaction solution was precipitated in MeOH after which the supernatant was decanted and the residue was dried in vacuo. A black, tar-like material was obtained.Other PPrS@AgNPs were prepared by adjusting the PPrS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AgCO2CF3 ratio. The sample is designated as PPrS@AgNP0.21 with 0.21 standing for the AgNP filling fraction ϕ in vol%.
AgCO2CF3 ratio. The sample is designated as PPrS@AgNP0.21 with 0.21 standing for the AgNP filling fraction ϕ in vol%.
Conclusions
We conclude that for the first time AgNPs could be used as a reinforcing agent for polydentate PPrS already at very low filling rates. AgNPs were incorporated by a simple in situ method, yielding nanocomposites with high colloidal stability against aggregation also at elevated temperatures. PPrS of high molar mass was converted from a viscous liquid to a soft material having viscoelastic properties of an unfastened network which makes the materials response elastic at mechanical stimulation but liquid-like on larger time scales. Yet, PPrS@AgNP0.30 approaches solid-like long-term suppression of flow due to a significant shift of the G′–G′′ crossover frequency ωc. The observed decelerated dynamics at low shear frequencies provide strong evidence for AgNP-imposed additional topological constraints. Calculations on polymer–particle dimensions substantiate a scenario where the chain's primitive paths are loosely trapped by AgNPs; thus generating a long-range entanglement-mediated polymer–particle network. In all, we believe that due to various metal type-dependent chemical, physical or biological features, the exploitation of metal nanoparticles as the reinforcing agent will rapidly gain momentum for a wide variety of liquids and also cross-linked polymers.Acknowledgements
The authors are indebted to DFG for financial support and to M. Böhm, R. Dersch, M. Müller, R. Giesa and P. Ohlendorf for technical support. We gratefully thank C. Kuttner and A. Fery at Physical Chemistry 2 of University of Bayreuth for performing and analyzing Raman measurements. Special thanks are addressed at M. Hofmann and E. Rößler at Experimental Physics 2 of University of Bayreuth for supporting with technical expertise.Notes and references
- R. Shenhar, T. B. Norsten and V. M. Rotello, Adv. Mater., 2005, 17, 657 CrossRef CAS.
- B. C. Sih and M. O. Wolf, Chem. Commun., 2005, 3375 RSC.
- S. Bokern, J. Getze, S. Agarwal and A. Greiner, Polymer, 2011, 52, 912 CrossRef CAS PubMed.
- J. Shan, M. Nuopponen, H. Jiang, T. Viitala, E. Kauppinen, K. Kontturi and H. Tenhu, Macromolecules, 2005, 38, 2918 CrossRef CAS.
- P. Schexnailder and G. Schmidt, Colloid Polym. Sci., 2009, 287, 1 CAS.
- J. Rojo, V. Díaz, J. M. de la Fuente, I. Segura, A. G. Barrientos, H. H. Riese, A. Bernad and S. Penadés, ChemBioChem, 2004, 5, 291 CrossRef CAS PubMed.
- M. Liang, I.-C. Lin, M. R. Whittaker, R. F. Minchin, M. J. Monteiro and I. Toth, ACS Nano, 2010, 4, 403 CrossRef CAS PubMed.
- C. Ayomonier, U. Schlotterbeck, L. Antonietti, P. Zacharias, R. Thomann, J. C. Tiller and S. Mecking, Chem. Commun., 2002, 3018 RSC.
- S. Gupta, M. Agrawal, M. Conrad, N. A. Hutter, P. Olk, F. Simon, L. M. Eng, M. Stamm and R. Jordan, Adv. Funct. Mater., 2010, 20, 1756 CrossRef CAS.
- W.-C. Lin and M.-C. Yang, Macromol. Rapid Commun., 2005, 26, 1942 CrossRef CAS.
- S.-W. Baek, J. Noh, C.-H. Lee, B. S. Kim, M.-K. Seo and J.-Y. Lee, Sci. Rep., 2013, 3, 3 Search PubMed.
- M. B. Müller, C. Kuttner, T. König, V. Tsukruk, S. Förster, M. Karg and A. Fery, ACS Nano, 2014, 8, 9410 CrossRef PubMed.
- C. Kuttner, P. C. Maier, C. Kunert, H. Schlaad and A. Fery, Langmuir, 2013, 29, 16119 CrossRef CAS PubMed.
- N. ten Brummelhuis, C. Diehl and H. Schlaad, Macromolecules, 2008, 41, 9946 CrossRef CAS.
- N. Hisano, H. Iwata, Y. Teramura, H. Chen and Y. Ikada, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 671 CrossRef CAS.
- I. Hussain, S. Graham, Z. Wang, B. Tan, D. C. Sherrington, S. P. Rannard, A. I. Cooper and M. Brust, J. Am. Chem. Soc., 2005, 127, 16398 CrossRef CAS PubMed.
- M. Ganesan, R. G. Freemantle and S. O. Obare, Chem. Mater., 2007, 19, 3464 CrossRef CAS.
- D. Thompson, J. P. Hermes, A. J. Quinn and M. Mayor, ACS Nano, 2012, 6, 3007 CrossRef CAS PubMed.
- J. P. Hermes, F. Sander, T. Peterle, C. Cioffi, P. Ringler, T. Pfohl and M. Mayor, Small, 2011, 7, 920 CrossRef CAS PubMed.
- T. Peterle, A. Leifert, J. Timper, A. Sologubenko, U. Simon and M. Mayor, Chem. Commun., 2008, 3438 RSC.
- J. P. Hermes, F. Sander, T. Peterle, R. Urbani, T. Pfohl, D. Thompson and M. Mayor, Chem. – Eur. J., 2011, 17, 13473 CrossRef CAS PubMed.
- J. P. Hermes, F. Sander, U. Fluch, T. Peterle, D. Thompson, R. Urbani, T. Pfohl and M. Mayor, J. Am. Chem. Soc., 2012, 134, 14674 CrossRef CAS PubMed.
- S. Bokern, Z. Fan, C. Mattheis, A. Greiner and S. Agarwal, Macromolecules, 2011, 44, 5036 CrossRef CAS.
- H. Pletsch, M. J. Schnepf and S. Agarwal, Chem. Mater., 2014, 26, 4805 CrossRef CAS.
- Q. Zhang and L. A. Archer, Langmuir, 2002, 18, 10435 CrossRef CAS.
- J. Yang, C.-R. Han, J.-F. Duan, F. Xu and R.-C. Sun, J. Phys. Chem. C, 2013, 117, 8223 CAS.
- Z. Zhu, T. Thompson, S.-Q. Wang, E. D. von Meerwall and A. Halasa, Macromolecules, 2005, 38, 8816 CrossRef CAS.
- A. Şerbescu and K. Saalwächter, Polymer, 2009, 50, 5434 CrossRef PubMed.
- L. Wang, G. Kilcher and N. Tirelli, Macromol. Chem. Phys., 2009, 210, 447 CrossRef CAS.
- K. Yurekli, R. Krishnamoorti, M. F. Tse, K. O. Mcelrath, A. H. Tsou and H.-C. Wang, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 256 CrossRef CAS.
- G. P. Baeza, A.-C. Genix, C. Degrandcourt, L. Petitjean, J. Gummel, R. Schweins, M. Couty and J. Oberdisse, Macromolecules, 2013, 46, 6621 CrossRef CAS.
- R. A. Riggleman, G. Toepperwein, G. J. Papakonstantopoulos, J.-L. Barrat and J. J. de Pablo, J. Chem Phys., 2009, 130, 244903 CrossRef PubMed.
- S. Jain, J. G. P. Goossens, G. W. M. Peters, M. van Duin and P. J. Lemstra, Soft Matter, 2008, 4, 1848 RSC.
- M. Surve, V. Pryamitsyn and V. Ganesan, Langmuir, 2006, 22, 969 CrossRef CAS PubMed.
- S. Sen, J. D. Thomin, S. K. Kumar and P. Keblinski, Macromolecules, 2007, 40, 4059 CrossRef CAS.
- J. B. Hooper and K. S. Schweizer, Macromolecules, 2005, 38, 8858 CrossRef CAS.
- M. Hofmann, A. Herrmann, A. A. Elfadl, D. Kruk, M. Wohlfahrt and E. A. Rössler, Macromolecules, 2012, 45, 2390 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: UV/Vis measurements; experiments on PPrS@AgNP thermal stability; G′ and G′′ master curves of PPrS@AgNP0.13, PPrS@AgNP0.21, PPrS@AgNP0.81 and PPrS@AgNP0.95. See DOI: 10.1039/c4nr06834c |
| This journal is © The Royal Society of Chemistry 2015 |