Tailoring the water structure and transport in nanotubes with tunable interiors†
Luis
Ruiz
a,
Yuanqiao
Wu
b and
Sinan
Keten
*ab
aDepartment of Mechanical Engineering, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208-3109, USA. E-mail: s-keten@northwestern.edu; Tel: +847-491-5282
bDepartment of Civil and Environmental Engineering, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208-3109, USA
First published on 15th October 2014
Abstract
Self-assembly of cyclic peptide nanotubes (CPNs) in polymer thin films has opened up the possibility of creating separation membranes with tunable nanopores that can differentiate molecules at the sub-nanometer level. While it has been demonstrated that the interior chemistry of the CPNs can be tailored by inserting functional groups in the nanopore lumen (mCPNs), a design strategy for picking the chemical modifications that lead to particular transport properties has not been established. Drawing from the knowledgebase of functional groups in natural amino acids, here we use molecular dynamics simulations to elucidate how bioinspired mutations influence the transport of water through mCPNs. We show that, at the nanoscale, factors besides the pore size, such as electrostatic interactions and steric effects, can dramatically change the transport properties. We recognize a novel asymmetric structure of water under nanoconfinement inside the chemically functionalized nanotubes and identify that the small non-polar glycine-mimic groups that minimize the steric constraints and confer a hydrophobic character to the nanotube interior are the fastest transporters of water. Our computationally developed experiments on a realistic material system circumvent synthetic challenges, and lay the foundation for bioinspired principles to tailor artificial nanochannels for separation applications such as desalination, ion-exchange and carbon capture.
Introduction
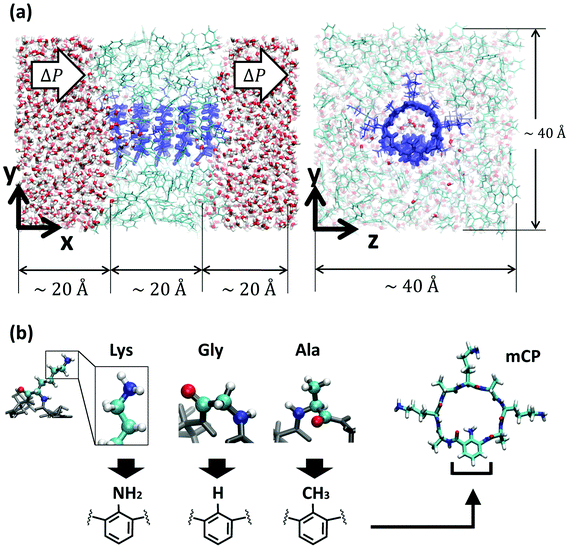
Today, there is a growing need for environmentally friendly separation membranes to address some of society's most pressing issues associated with molecular selective transport applications such as carbon capture, water desalination or fuel cell technology.1–4 In pursuit of overcoming some of the limitations of conventional nanoporous membranes, namely, control of the pore size distribution and pore continuity across the membrane, composite systems with carbon nanotubes (CNTs) embedded in an impermeable polymer matrix have been proposed.5–8 However, despite the promise of CNTs as fast transporters, tailoring their interior surface chemistry still remains challenging. This lack of tunability restricts the implementation of biomimetic concepts that could otherwise improve the selectivity and functionality of the membranes. Biological channels are a great source of inspiration as they display a great control over the molecular selectivity that arises from their chemical heterogeneity. Prime examples include aquaporins, ion channels or bacterial porins such as gramicidin.9–11 However, in order to be able to implement biomimetic concepts in engineered systems, a synthetic platform that allows more design flexibility is required.Organic nanotubes formed by stacked cyclic peptides stabilized by hydrogen bonds (cyclic peptide nanotubes, or CPNs) are particularly promising candidates as biomimetic synthetic nanopores due to their exceptional mechanical properties, possible control over the pore size at the sub-nanometer level, and highly tunable chemistry.12–15 Flexible thin nanoporous membranes containing vertically aligned subnanometer CPNs have been generated by co-assembling polymer conjugated cyclic peptides in block copolymer micro domains,7 validating the feasibility of the design. Furthermore, the possibility of chemical functionalization of the CPN lumen by insertion of an unnatural amino acid in the peptide sequence containing a functional group that points towards the interior of the ring (referred as modified cyclic peptides, or mCPs) has been recently unveiled.14 This synthetic route opens the door to the application of biomimetic concepts to engineered nanotubes, and that, together with the commensurability of the inter-ring spacing with the distances between functional groups observed in biological systems makes mCPNs a unique platform to test biomimetic designs and investigate features of biological channels.
The study of water permeation through biological and synthetic nanochannels has been a prevalent topic of discussion in recent years due to the importance of water purification applications and the biological relevance of the problem.16–24 Under nanoscale confinement, water has been observed to display physical attributes substantially different from those of the bulk, leading to transport properties that differ greatly from the predictions of classical continuum theories.25–28 For example, it has been shown that the flux of water under one dimensional nanoconfinement in carbon nanotubes greatly exceeds classical hydrodynamic predictions,25 highlighting the potential of sub-nanometer hydrophobic channels as high throughput systems for molecular transport applications. Another important aspect to consider besides the size of the channel is the interior chemistry. It has been shown in idealized nanochannels that water permeability is maximized for intermediate values of the interaction between the pore and the water. While highly polar interiors (i.e. hydrophilic pore) facilitate the entry of water, the translocation across the channel is diminished due to the fact that water molecules spend longer times inside the pore. On the other hand, low polarity interiors (i.e. hydrophobic pore) impose a solvation energy barrier that reduces the entrance of molecules into the pore, resulting again in low permeability.
The structure and transport properties of water through conventional CPNs have been previously studied.29–32 However, due to the novelty of the synthetic route for chemically functionalizing the cyclic peptides, the molecular transport properties of the most promising mCPNs remain currently unexplored. Here, we employ computational modeling to test bioinspired designs in an engineering platform beyond the physiological context. We aim to understand the role that the chemistry of the functional group in the mutated amino acid plays in the organization and permeability of water in bioinspired mCPNs. For this purpose, we focus on a model system. To elucidate this, we use atomistic Molecular Dynamics (MD) simulations under equilibrium conditions as well as non-equilibrium MD (NEMD) simulations with different hydrostatic pressure levels to drive water flow through the nanotube (Fig. 1a). We sample a variety of functional groups, specifically we use chemistries mimicking deprotonated lysine (large, polar), glycine (small, non-polar), and alanine (large, non-polar) amino acid side-chains (Fig. 1b). The charge distributions of the different functional groups are shown in Fig. S1.† In the following sections of the paper, we first present a summary of the computational methodology employed. Next, we analyze the structure of water inside the nanotubes and identify the best performers in terms of unidirectional water permeation under pressure. Finally, we reconstruct the energy profiles of water along the pores and link their performance to the free energy profile roughness. We conclude our analysis by providing guidelines for future synthesis efforts towards nanotubes with tailored transport properties.
Results and discussion
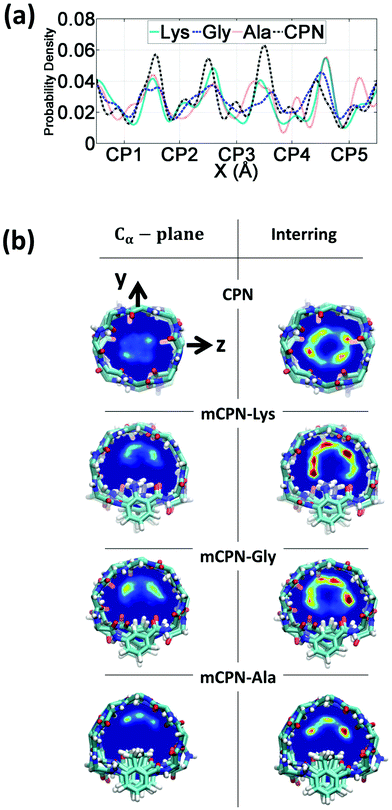
First, we analyze the distribution and orientation of the water molecules inside the different mCPNs. The organization of water has a critical impact on the transport and selectivity properties of nanotubes since it governs aspects such as the coordination of ions inside the pores or the transport mechanism of water molecules (e.g. the single-file water structure requires concerted motion inside the pore for translocation).29,33,34 The orientational configuration of water also has implications on the transport properties of the nanotubes. For example, the dipole inversion of the single-file water wire can prevent proton transport through the Grotthuss mechanism, as is the case of aquaporins.35The density profiles of water along the different nanotubes (Fig. 2a), as well as the cross-sectional density heat maps (Fig. 2b), show that the water molecules preferentially occupy the inter-ring spacing as opposed to the Cα-plane regions. This structure is observed for both the conventional CPN and the different mCPNs, and is a result of the combination of steric constraints imposed by the cyclic peptide backbone and favorable interactions between the water molecules and the carbonyl groups of the peptides. To illustrate how the size and chemistry of the functional group shape the configuration of water in the cross-section of the nanotubes, we build density heat maps that show the probability of water molecules being in the Cα-plane and the inter-ring regions (Fig. 2b). Along the y-axis, an asymmetric distribution is observed. The water molecules, pushed by the functional group, tend to occupy the upper part of the nanotube, particularly in the Cα-plane regions (Fig. 2b). The asymmetry of the distribution is more pronounced for the large, hydrophobic functional group (mCPN-Ala), suggesting that steric constraints are the cause of the shift of the distribution (Fig. S2†). The chemistry of the functional group also plays a role in determining the wettability of the pore. Favorable interactions between the water molecules and the NH2 group in the mCPN-Lys drive water molecules to occupy the space closer to the functional group. Along the z-axis, the heat maps show highly populated regions on both sides of the functional group. A closer look at the probability distributions reveals that water molecules tend to concentrate on the side of the carbonyl group of the unnatural amino acid (Fig. S3†). Due to the antiparallel stacking of the rings, the location of the carbonyl group alternates along the nanotube, affecting the distribution of the water molecules. Our analysis suggests that the polarity and the steric repulsions imposed by the functional group, together with electrostatic interactions between the carbonyl groups and the water molecules, are responsible for the arrangement of water molecules in this fashion inside the nanotubes. The asymmetric water structure that we just described has not been previously observed, and it is substantially different from that in conventional CPNs or carbon nanotubes (CNTs) of equivalent size (e.g. (8,8) with a diameter of ∼1 nm), characterized by cylindrically symmetrical density distributions.30,36
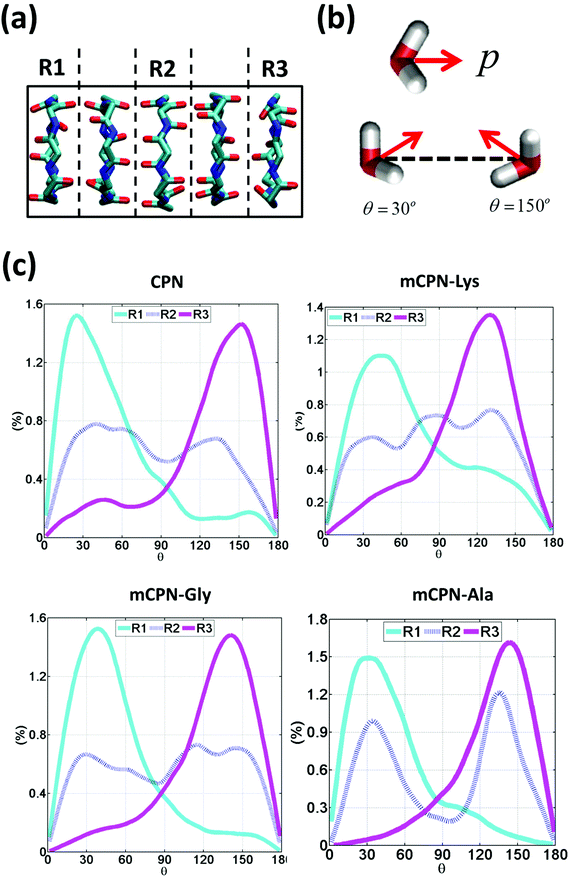
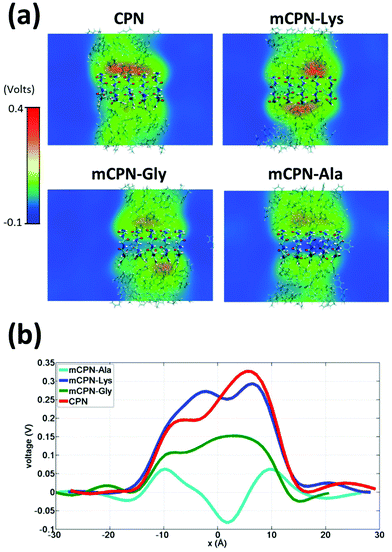
Next, we analyze the orientation of water molecules inside the nanotube and the electrostatic signature of the different systems. The orientation angle of the water molecules with respect to the axis of the nanotube is characterized by the existence of very distinctive peaks in the probability distribution at approximately 30° and 150° on the left and right ends of the nanotube, respectively (regions R1 and R3 as shown in Fig. 3). The strong orientation at the ends of the nanotube arises from the tendency of the water dipoles to align with the electrostatic potential, higher in the membrane and zero in the water reservoirs (Fig. 4a). The symmetrical angle on both ends of the nanotube implies a dipole inversion upon translocation, corroborating previous studies on CPNs.30,32 Due to the symmetry of the system, the center of the nanotube (region R2 in Fig. 3) is where the dipole inversion is expected to occur, leading to a flat probability distribution of the orientational angle in this region. This is the case for the CPN, mCPN-Lys, and the mCPN-Gly. On the other hand, the orientation angle distribution in the central region of the mCPN-Ala shows a bimodal shape (Fig. 3). This can be explained by the distinct electrostatic signature of this system that exhibits a minimum at the center of the nanotube, a feature that is not displayed by the other types of mCPNs (Fig. 4b). This minimum in the electric potential generates gradients of opposite directions that may cause the bimodal shape of the orientation angle distribution. A snapshot of the water molecules inside the mCPN-Ala illustrates the situation (Fig. 5d).
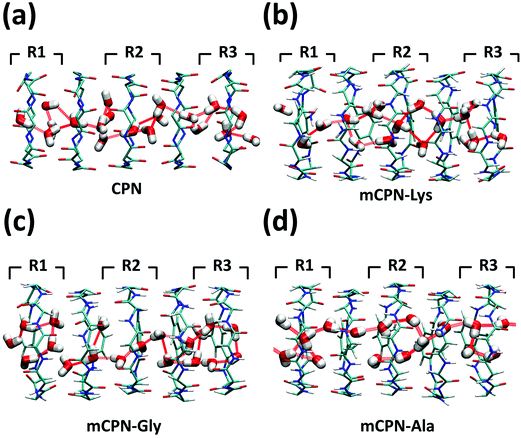 | ||
| Fig. 5 Snapshots of the water structure inside the (a) CPN, (b) mCPN-Lys, (c) mCPN-Gly, and (d) mCPN-Ala. Hydrogen bonds between the water molecules are shown as dashed red lines. | ||
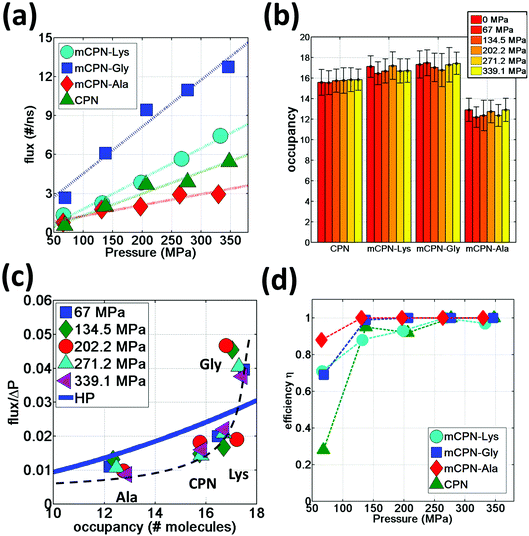
A question that persists in the literature of molecular transport under nanoconfinement is whether classical continuum theories can be applied to predict flow rates in nanochannels. For example, can two pores with similar pore diameters exhibit distinctly different flow rates? The diameter of the pore controls occupancy, that is, the number of molecules that can be accommodated on average within the nanochannel. Here, we examine the occupancy and the permeability of different nanotubes under applied pressure and compare it to simple hydrodynamic predictions of the Hagen–Poiseuille equation.
We observe that the occupancies of the mCPNs are mainly controlled by the size and polarity of the functional groups, with smaller size and higher polarity leading to higher occupancy. The mCPN-Ala, which contains large hydrophobic groups, displays an occupancy of ∼12 molecules, the lowest of all the cases studied (Fig. 6b). On the other hand, the mCPN-Gly, containing small hydrophobic groups, exhibits similar occupancy to the case with large hydrophilic groups, mCPN-Lys (∼17 molecules), suggesting that steric effects can be compensated with the hydrophilicity of the functional group. These nanotubes display similar occupancies despite the fact that their interior volume is different (large functional groups lead to smaller interior volume and vice versa). This observation is in clear contrast to the macroscopic viewpoint where channels with similar occupancies necessarily imply similar interior volumes, and highlights the critical role that the chemistry plays on the nanoscale.
In order to quantify the permeability through the different nanotubes, we define net flux and flow of water. We define net flux as the difference between the number of permeation events in the (+x) (direction of the gradient of the applied pressure) and (−x) directions: flux = (+x) − (−x) . Flow, on the other hand, is defined as the sum of the permeation events in both directions: flow = (+x) + (−x). Fig. 6a shows the water flux as a function of applied pressure for different nanotube chemistries. The data can be fit by a linear trend with reasonable accuracy, suggesting that while the nanoscale flow is not expected to strictly follow the Hagen–Poiseuille (HP) equation (the continuum hydrodynamics equation governing laminar flow along a circular pipe), the mass transport relationship Q ∼ ΔP, where Q is the volumetric flux and ΔP the pressure difference, still holds for the wide range of pressure differences studied here. This scaling relationship has also been shown to hold on the nanoscale in previous computational studies on CPNs31 and CNTs.37 The flux in mCPNs (Fig. 6a) is comparable to that of biological channels of comparable length, with aquaporins displaying a flux of ∼1–2 water molecules per nanosecond at physiological osmotic pressure (approximately equivalent to a hydrostatic pressure of 10 MPa),38 and aquaglyceroporins exhibiting a flux of ∼5 ns−1 for a pressure of P = 197 MPa according to a computational study.39 It is worth mentioning that, while ballpark comparisons between different studies and methodologies may be acceptable if done with care, precise quantitative comparisons should be avoided due to the possible dependence of the results from the different studies on simulation parameters and system set-up.
We also put to the test the scaling Q ∼ R4 of the HP equation. The interior volume of the nanotubes can be determined using Vint = OH2O·VH2O, where OH2O is the occupancy number, and VH2O is the volume of a water molecule. The volume of the channel scales with the radius as Vint ∼ R2. Therefore the scaling of the HP equation between the flux and the occupancy number is Q ∼ (OH2O)2. The normalized flux versus occupancy data, together with the prediction of the HP equation is shown in Fig. 6c. We find a certain correlation between the occupancies of the different nanotubes and their flux, with lower occupancy leading to lower permeability and vice versa. The exact relationship is unclear, and the HP equation seems unable to capture the trend. This highlights the fact that on the nanoscale, other aspects besides the dimensions of the pore (e.g. the volume), such as steric constraints and electrostatic effects that shape the energy profile of water flowing through the nanotube, play important roles in determining the permeability through the nanotubes. For example, mCPN-Gly and mCPN-Lys exhibit very similar occupancy values, but the permeability is very different between the two.
Another important aspect of nanoscale molecular transport is the efficiency of the systems in transporting water in a unidirectional fashion. It has been observed in CNTs that thermal fluctuations on the reservoirs produce backflows even under pressurized conditions, especially for short nanotubes.40 In order to measure the efficiency of the mCPNs at transporting water in a unidirectional fashion, we define the variable η = flux/flow, where η = 1 implies unidirectional transport and η = 0 indicates the same number of permeation events on both (+x) and (−x) directions of the nanotube. It has been reported for (8,8) carbon nanotubes (CNTs) of similar dimensions as our mCPNs (∼2 nm length, with 1.08 nm diameter), efficiency values of η ≈ 0.1, η ≈ 0.4, and η ≈ 0.7, for hydrostatic applied pressures of P ≈ 36.2 MPa, P ≈ 181 MPa, and P ≈ 362 MPa, respectively.33 Our results show that mCPNs are, in general, more efficient than CNTs (Fig. 6d). Even for the lowest pressure applied (P ≈ 67 MPa), mCPNs display efficiencies on the order of 0.7 to 0.9. Particularly, the hydrophobic mCPNs, both mCPN-Gly and mCPN-Ala, exhibit complete unidirectional transport (η = 1) for pressures as low as ∼140 MPa, while the efficiency of (8,8) CNTs at a higher pressure of 181 MPa is around η ≈ 0.433 The higher efficiency of the mCPNs can be attributed to the rougher energy landscape, compared to the smooth landscape characteristic of CNTs. The periodic energy barriers observed in our systems will decrease the reach of the effects caused by thermal fluctuations in the reservoirs.
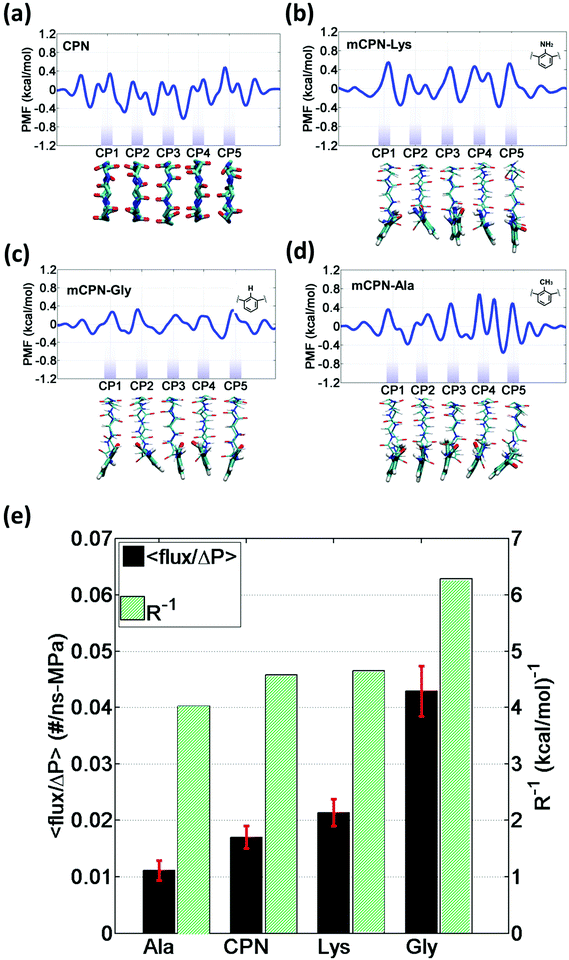
In order to gain a better understanding of how different functional groups affect the transport properties of the mCPNs, we reconstruct the potential of mean force (PMF) profiles, which represent how the free energy of a water molecule changes as a function of the position along the nanotube. We do so by inverting the probability distributions of water molecules along the nanotube calculated over the equilibrium simulations, ΔF(x) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log (P(x)). The PMF profiles are qualitatively similar for all the cases, characterized by periodic energy barriers whose magnitude depends on the steric constraints and electrostatics imposed by the functional groups on the water molecules. For the CPN, the free energy profile is characterized by periodic energy barriers of the order of the thermal energy (kT = 0.593 kcal mol−1), with the free energy minima located in the inter-ring regions and other smaller local minima located in the Cα-plane regions, in agreement with previous studies.30,32 The minima located in the inter-ring spacing arise from the fact that the steric constraints are minimized between rings and that the water molecules favorably interact with the polar moieties of the CPs, partially compensating for the lack of coordination with respect to the bulk. The local minima at the Cα-plane regions correspond to a weak metastable state where the water molecule is hydrated by the neighboring water molecules in the contiguous inter-ring spacing. Due to the steric repulsions imposed by the functional groups on Cα-plane regions, these metastable states are mostly absent in mCPNs. Small energy wells can be found at the interface between the nanotube and the water reservoirs, indicating that water spends significant time in the vestibules. The minimum in the vestibule is followed by an energy barrier located at both terminal rings of the nanotube. The wavy shape of the PMF profiles results in a “hopping” mechanism of water translocation. Under equilibrium conditions, and given the symmetry of the system, the PMF profiles should, in principle, be symmetric. This is the case of the CPN (Fig. 7a), where the structure is relatively rigid due to the constraints in the alpha carbons of the backbone. The partial lack of symmetry observed in some of the PMF profiles of mCPNs can be attributed to two factors. The first factor is the limited sampling of the phase space during the finite simulation time that can cause some irregularities in the profiles. The second factor is related to the fact that the unnatural amino acid is not constrained and can fluctuate. The flexibility of the unnatural amino acid in different rings, illustrated by the snapshots shown in Fig. 7, can give rise to stochastic fluctuations that may lead to deviations from a symmetric profile. In order to compare the different landscapes, we define the roughness of a PMF profile as the average energy difference between the maxima and minima with respect to the moving average of the profile at that location:
log (P(x)). The PMF profiles are qualitatively similar for all the cases, characterized by periodic energy barriers whose magnitude depends on the steric constraints and electrostatics imposed by the functional groups on the water molecules. For the CPN, the free energy profile is characterized by periodic energy barriers of the order of the thermal energy (kT = 0.593 kcal mol−1), with the free energy minima located in the inter-ring regions and other smaller local minima located in the Cα-plane regions, in agreement with previous studies.30,32 The minima located in the inter-ring spacing arise from the fact that the steric constraints are minimized between rings and that the water molecules favorably interact with the polar moieties of the CPs, partially compensating for the lack of coordination with respect to the bulk. The local minima at the Cα-plane regions correspond to a weak metastable state where the water molecule is hydrated by the neighboring water molecules in the contiguous inter-ring spacing. Due to the steric repulsions imposed by the functional groups on Cα-plane regions, these metastable states are mostly absent in mCPNs. Small energy wells can be found at the interface between the nanotube and the water reservoirs, indicating that water spends significant time in the vestibules. The minimum in the vestibule is followed by an energy barrier located at both terminal rings of the nanotube. The wavy shape of the PMF profiles results in a “hopping” mechanism of water translocation. Under equilibrium conditions, and given the symmetry of the system, the PMF profiles should, in principle, be symmetric. This is the case of the CPN (Fig. 7a), where the structure is relatively rigid due to the constraints in the alpha carbons of the backbone. The partial lack of symmetry observed in some of the PMF profiles of mCPNs can be attributed to two factors. The first factor is the limited sampling of the phase space during the finite simulation time that can cause some irregularities in the profiles. The second factor is related to the fact that the unnatural amino acid is not constrained and can fluctuate. The flexibility of the unnatural amino acid in different rings, illustrated by the snapshots shown in Fig. 7, can give rise to stochastic fluctuations that may lead to deviations from a symmetric profile. In order to compare the different landscapes, we define the roughness of a PMF profile as the average energy difference between the maxima and minima with respect to the moving average of the profile at that location: 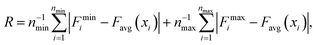 where Fmini and Fmaxi are the values of the free energy of the ith minimum or maximum, respectively, nmin and nmax are the total number of minima and maxima, and Favg(xi) is the value of the moving average of the profile at the location of the ith minimum or maximum. In Fig. 7(e), we show that as the roughness of the profile decreases (the inverse of the roughness, which is plotted in the panel, increases) the normalized flux increases. In other words, smoother landscapes lead to higher flux. The mCPN-Gly, which achieves the highest water flux, also exhibits the smoothest free energy landscape. On the other hand the roughest landscape corresponds to the mCPN-Ala, which showed the lowest permeability.
where Fmini and Fmaxi are the values of the free energy of the ith minimum or maximum, respectively, nmin and nmax are the total number of minima and maxima, and Favg(xi) is the value of the moving average of the profile at the location of the ith minimum or maximum. In Fig. 7(e), we show that as the roughness of the profile decreases (the inverse of the roughness, which is plotted in the panel, increases) the normalized flux increases. In other words, smoother landscapes lead to higher flux. The mCPN-Gly, which achieves the highest water flux, also exhibits the smoothest free energy landscape. On the other hand the roughest landscape corresponds to the mCPN-Ala, which showed the lowest permeability.
It was recently reported that non-single-file water flows can be advantageous for practical applications as the decay of the permeability with the length of the nanotube (i.e. the longer the nanotube the lower the permeability) is slower than for single-file water flows.33 This is due to the fact that concerted motion on the length-scale of the nanotube is not required for translocation of water molecules in non-single file flows. Although for biological applications, the length of the nanotubes studied here is directly relevant (the length of biologically occurring channels is ∼2 nm), the scaling of flux with the length of the mCPNs may have important consequences for technological applications as efficient nanopores in thin-film membranes where the nanotubes would need to span the entire film which can be tens of nanometers thick.7 In mCPNs, we do not observe single-file water patterns and the periodic energy barriers to water permeation shown in the PMF profiles are on the order of the thermal energy. Based on these principles, we would expect slow decay of the flux when the length of mCPNs is increased, although further work is necessary to corroborate this hypothesis. Furthermore, modulating the size of the rings by decreasing the number of amino acids is likely to lead to systems where single file flow can be achieved. The simulation methodology and transport metrics, such as the roughness criterion established here, can be adopted for future studies on such systems.
Conclusions
In this paper, we showed that the insertion in the sequence of cyclic octapeptides of an unnatural amino acid with a functional group pointing inwards (mCPs) has tremendous implications on the transport properties of the nanotubes, beyond the predictions of continuum hydrodynamics. We discovered that the particular nanoconfinement environment provided in mCPNs, determined by the supramolecular character of the nanotubes and the steric constraints and electrostatics imposed by the functional group, lead to a novel non-single-file water pattern. Along the axis of the nanotube, this structure consists of water molecules preferentially occupying the inter-ring spacing. In the cross section, water occupies the space on both sides of the functional group and the upper region of the nanotube, opposed to the location of the unnatural amino acid.The orientation angle of water molecules in mCPNs is shown to undergo a transition upon permeation, from 30° to 150° on the left and the right of the nanotube respectively. This dipole inversion is explained by the electrostatic potential of the system, higher in the membrane and lower in the reservoirs. We showed that the specific chemistry of the functional group plays an important role in determining the electrostatic field, and hence the orientation of water in the central region of the nanotubes. In particular, the mCPN-Ala displays a distinct electrostatic signature that leads to a bimodal orientational angle distribution in the middle region of the nanotube, in contrast to the other mCPNs that exhibit flatter distributions in this transitional region.
We hypothesize here that the novel highly tunable water pattern in mCPNs (which depends on the size and polarity of the functional group of the unnatural amino acid) may have important implications on the selectivity properties of the nanotubes. The enhanced steric constraints observed in the mCPN-Lys or mCPN-Ala, compared to regular CPNs or CNTs, could potentially increase the desolvation energy barrier of ions or charged solutes, therefore increasing the rejection rate of charged species by the nanotubes. Moreover, the dipole inversion upon translocation and the absence of single-file water in the nanotubes may be useful in preventing proton translocation.
The reconstructed PMF profiles revealed periodic energy barriers whose magnitude depends on the electrostatic signature and steric constraints imposed by the functional groups. The mCPN-Gly, characterized by small hydrophobic H groups, presented the smoothest energy landscape and highest occupancy, and therefore it exhibited the largest flux of water under pressurized conditions. In the mCPN-Lys case, the NH2 groups impose large steric constraints that are partially compensated by the hydrophilicity of the group, leading to high occupancy values and permeability exceeding that of CPNs. The worst performer was the mCPN-Ala, which contains large hydrophobic CH3 groups and exhibits the roughest energy landscape.
We also demonstrated that mCPNs are particularly efficient unidirectional transporters, even under unfavorable conditions of low applied pressure (∼63 MPa) and short nanotube length (∼2 nm). This is of tremendous importance for biological applications, where the length of the nanotube can be limited by the thickness of the membrane layer (∼4–5 nm for lipid bilayers) and the external pressure is determined by the osmotic difference under physiological conditions.
In summary, our analysis establishes the molecular basis of water transport through a rich variety of chemistries of mCPNs, setting the cornerstone for future investigations towards the design and development of mCP-based biomimetic nanopores with heterogeneous interior chemistry.
Methods
The atomistic model consists of a nanotube embedded in a low dielectric membrane placed between two water reservoirs (Fig. 1). The simulation cell is rectangular, with approximate dimensions of 60 × 40 × 40 Å3. Periodic boundary conditions (PBCs) are applied in all directions. Although the visualization of the system suggests the existence of two water reservoirs, due to PBCs, only one reservoir exists. The low dielectric membrane is made of toluene molecules packed in a random fashion at its equilibrium density in the liquid state (0.87 g mL−1). The nanotube, oriented along the x-axis, consists of 5 cyclic peptides with an approximate length of 20 Å, spanning the thickness of the membrane. The cyclic peptides are pre-arranged in an anti-parallel beta-sheet configuration and are set apart from each other at approximately their equilibrium distance of ∼4.8 Å. The chemical makeup of the regular cyclic peptide is cyclo[(D-Ala-Lys)4] and that of the chemically functionalized cyclic peptides is cyclo[(D-Ala-Lys)3-D-Ala-R], where R stands for the unnatural amino-acid. The unnatural amino acid consists of a benzene ring with a functional group pointing towards the interior of the cyclic peptide. We study 3 different functional group chemistries NH2, H, and CH3 inspired by the lysine, glycine, and alanine amino acid side chains respectively. The partial charges of the functional groups studied here are shown in Fig. 1 of the ESI (Fig. S1).† We refer to the different types of chemically functionalized nanotubes as mCPNs, followed by the abbreviation of the amino acid that the functional group mimics (e.g. mCPN-Ala). CPN stands for a nanotube formed by regular octapeptides without unnatural amino acids. All the nanotube types are simulated under equilibrium conditions and 5 levels of hydrostatic pressure differences (from ∼67 MPa to ∼339 MPa), making a total of 24 different cases. All of the nanotubes are homomeric (i.e. all of the cyclic peptides in the nanotube have the same chemistry).All the simulations presented in this paper are carried out using the parallel molecular dynamics software NAMD2.41 The molecular visualization package VMD,42 in combination with TCL scripts and the program Matlab, have been used for the post process analysis. The CHARMM36 force-field43 is used for the protein nanotubes. We use a TIP3 standard model for water.44 The CHARMM general force-field (CGenFF) is used for the toluene membrane. CHARMM36 and CGenFF are fully compatible force-fields. The unnatural amino acids studied here (Fig. 2) are not fully parameterized in the CHARMM force-field. In order to find the missing parameters, we use the software ParamChem 0.9.7.145 with the CGenFF 2b8 force-field.46 The software outputs the values for the missing parameters together with a penalty measurement that estimates the quality of the prediction. Penalty values larger than 50 are considered poor quality and require extensive validation. All the penalties obtained for the parameters in this study are within the acceptable range, with most of the parameters having penalties of zero and only a few parameters with penalties in the range from 10 to 20. The parameters corresponding to the angles and dihedrals of the peptide bond between the unnatural and the regular amino-acids are set equal to the peptide bond between two regular amino-acids.
The same simulation protocol is followed for all the cases. A time step of 1 fs is used for all the simulations. After minimization of the system for 1000 steps using the conjugate gradient and line search algorithm, we equilibrate the system in the NPT ensemble (constant number of particles, pressure and temperature) at T = 298 K, P = 1 atm. The pressure is controlled using a modified Nosé–Hoover method in which Langevin dynamics is used to control the fluctuations in the barostat.47 A damping coefficient of 7 ps−1 is used to control the temperature. The electrostatic interactions are calculated using the particle mesh Ewald (PME) method.48 We equilibrate the system for 1.5 ns, during which the Cα of the CPs are constrained in the x-direction (the longitudinal direction of the nanotube). Under these constraints the CPs are allowed to rotate and move just in the plane of the rings, maintaining the inter-ring equilibrium distance. In the absence of constraints, the CPN has been seen to tilt in low dielectric membranes.49–51 While this process may be of interest in certain contexts, here we are only interested in the transport mechanisms across the nanotube. Our constraints, despite preventing the tilt of the nanotube, still permit ring rotation and in-plane displacement that allow maximization of the inter-ring hydrogen bond formation and therefore minimize the energy of the system. Similar protocols have been used in previous studies on the transport in regular CPNs.30,32,52
After equilibration, we study water transport through the nanotubes under both equilibrium conditions (Eq-MD) and under different levels of hydrostatic pressure. All of the simulations, after equilibration of the system, are carried out using the NVT ensemble (constant number of particles, volume and temperature) at T = 298 K. To avoid large displacements of the nanotube or the membrane in the x-direction due to the applied pressure, the Cα of the cyclic peptides and the carbon linking the methyl group and the benzene ring in the toluene molecules are constrained by harmonic springs with a spring constant of 10 kcal mol−1 Å2 to their original positions. The same constraints are applied during the Eq-MD simulations. The Eq-MD simulations are run for 50 ns, while the simulations under pressurized flow, more computationally expensive, are run for approximately 20 ns after the equilibration process. The hydrostatic pressure difference is established across the membrane following the method proposed by Zhu et al.39 In this method a constant force, f, is applied to the oxygen atoms of the water molecules in a system with PBCs. In order to minimize the artifacts introduced by the external force in the transport mechanisms of water close to the nanotubes, we only apply the force to the water molecules in the reservoirs that are farther than 3 Å from the nanotube backbone. The pressure difference induced, assuming a stationary state, is ΔP = nf/A, where n is the number of water molecules and A is the cross-section of the system. We study 5 different pressure differences: 67, 134.5, 202.2, 271.2, and 339.1 MPa.
In order to calculate the electrostatic potential heat maps and one-dimensional profiles along the nanotube axis we used the PMEPot plugin from the VMD program.53 This software allows calculating a smoothed electrostatic potential grid of the system using the Particle Mesh Ewald (PME) method. The mean electrostatic field of the system is calculated as the average of the instantaneous electric field from 5000 frames taken evenly spaced through the entire simulation. For this calculation, we used a grid of 60 × 44 × 44 points in the x, y and z directions respectively and a Ewald factor of 0.25.
The results reported here should be treated as semi-quantitative due to their possible dependence on the choice of atomistic force-field, model of water employed or value of the thermostat damping parameter.54 However, the observed trends are expected to be held in a physical context.
Acknowledgements
The work presented here is funded by the National Science Foundation (DMREF award CBET-1234305). The authors acknowledge the support from the Departments of Civil and Environmental Engineering and Mechanical Engineering at Northwestern University, as well as the Northwestern University High Performance Computing Center for a supercomputing grant. We thank our collaborators Ting Xu and Brett Helms for helpful discussions on the physical properties of chemically functionalized cyclic peptide nanotubes.References
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- T. C. Merkel, H. Lin, X. Wei and R. Baker, J. Membr. Sci., 2010, 359, 126–139 CrossRef CAS PubMed.
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- Z. Niu, L. Liu, L. Zhang and X. Chen, Small, 2014, 10, 3434–3441 CrossRef CAS PubMed.
- B. J. Hinds, N. Chopra, T. Rantell, R. Andrews, V. Gavalas and L. G. Bachas, Science, 2004, 303, 62–65 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- T. Xu, N. Zhao, F. Ren, R. Hourani, M. T. Lee, J. Y. Shu, S. Mao and B. A. Helms, ACS Nano, 2011, 5, 1376–1384 CrossRef CAS PubMed.
- H. Verweij, M. C. Schillo and J. Li, Small, 2007, 3, 1996–2004 CrossRef CAS PubMed.
- E. Gouaux and R. MacKinnon, Science, 2005, 310, 1461–1465 CrossRef CAS PubMed.
- B. L. de Groot and H. Grubmüller, Science, 2001, 294, 2353–2357 CrossRef CAS PubMed.
- S. Bernèche and B. Roux, Structure, 2005, 13, 591–600 CrossRef PubMed.
- L. Ruiz, P. Vonachen, T. D. Lazzara, T. Xu and S. Keten, Nanotechnology, 2013, 24 Search PubMed.
- A. C. D. Jennifer and Ç. Tahir, Nanotechnology, 2010, 21, 115703 CrossRef PubMed.
- R. Hourani, C. Zhang, R. van der Weegen, L. Ruiz, C. Li, S. Keten, B. A. Helms and T. Xu, J. Am. Chem. Soc., 2011, 133, 15296–15299 CrossRef CAS PubMed.
- R. Chapman, M. Danial, M. L. Koh, K. A. Jolliffe and S. Perrier, Chem. Soc. Rev., 2012, 41, 6023–6041 RSC.
- A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180 CrossRef CAS PubMed.
- L. S. King, D. Kozono and P. Agre, Nat. Rev. Mol. Cell Biol., 2004, 5, 687–698 CrossRef CAS PubMed.
- M. Kumar, M. Grzelakowski, J. Zilles, M. Clark and W. Meier, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20719–20724 CrossRef CAS PubMed.
- T. Humplik, J. Lee, S. C. O'Hern, B. A. Fellman, M. A. Baig, S. F. Hassan, M. A. Atieh, F. Rahman, T. Laoui, R. Karnik and E. N. Wang, Nanotechnology, 2011, 22, 292001 CrossRef CAS PubMed.
- B. Corry, J. Phys. Chem. B, 2007, 112, 1427–1434 CrossRef PubMed.
- N. Savage and M. Diallo, J. Nanopart. Res., 2005, 7, 331–342 CrossRef CAS.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- Q. Chen, L. Meng, Q. Li, D. Wang, W. Guo, Z. Shuai and L. Jiang, Small, 2011, 7, 2225–2231 CrossRef CAS PubMed.
- N. Modi, M. Winterhalter and U. Kleinekathofer, Nanoscale, 2012, 4, 6166–6180 RSC.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190 CrossRef CAS PubMed.
- O. Beckstein and M. S. P. Sansom, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7063–7068 CrossRef CAS PubMed.
- S. Joseph and N. R. Aluru, Nano Lett., 2008, 8, 452–458 CrossRef CAS PubMed.
- M. Thomas, B. Corry and T. A. Hilder, Small, 2014, 10, 1453–1465 CrossRef CAS.
- M. Engels, D. Bashford and M. R. Ghadiri, J. Am. Chem. Soc., 1995, 117, 9151–9158 CrossRef CAS.
- J. Liu, J. Fan, M. Tang and W. Zhou, J. Phys. Chem. A, 2010, 114, 2376–2383 CrossRef CAS PubMed.
- J. Liu, J. Fan, M. Tang, M. Cen, J. Yan, Z. Liu and W. Zhou, J. Phys. Chem. B, 2010, 114, 12183–12192 CrossRef CAS PubMed.
- J. Comer, F. Dehez, W. Cai and C. Chipot, J. Phys. Chem. C, 2013, 117, 26797–26803 CAS.
- J. Su and H. Guo, J. Phys. Chem. B, 2012, 116, 5925–5932 CrossRef CAS PubMed.
- C. Peter and G. Hummer, Biophys. J., 2005, 89, 2222–2234 CrossRef CAS PubMed.
- M. Ø. Jensen, E. Tajkhorshid and K. Schulten, Biophys. J., 2003, 85, 2884–2899 CrossRef CAS.
- I. Hanasaki and A. Nakatani, J. Chem. Phys., 2006, 124, 174714 CrossRef PubMed.
- J. A. Thomas and A. J. H. McGaughey, Nano Lett., 2008, 8, 2788–2793 CrossRef CAS PubMed.
- M. Borgnia, S. Nielsen, A. Engel and P. Agre, Annu. Rev. Biochem., 1999, 68, 425–458 CrossRef CAS PubMed.
- F. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2002, 83, 154–160 CrossRef CAS.
- G. Zuo, R. Shen, S. Ma and W. Guo, ACS Nano, 2009, 4, 205–210 CrossRef PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS PubMed.
- H. S. Kim, J. D. Hartgerink and M. R. Ghadiri, J. Am. Chem. Soc., 1998, 120, 4417–4424 CrossRef CAS.
- H. Hwang, G. C. Schatz and M. A. Ratner, J. Phys. Chem. A, 2008, 113, 4780–4787 CrossRef PubMed.
- M. Tarek, B. Maigret and C. Chipot, Biophys. J., 2003, 85, 2287–2298 CrossRef CAS.
- H. Hwang, G. C. Schatz and M. A. Ratner, J. Phys. Chem. B, 2006, 110, 26448–26460 CrossRef CAS PubMed.
- A. Aksimentiev and K. Schulten, Biophys. J., 2005, 88, 3745–3761 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Three figures regarding some details of the analysis presented here. The first figure shows the charge distribution of the different functional groups explored. The second and third figures contain density profiles of water along orthogonal directions of the nanotube cross section. See DOI: 10.1039/c4nr05407e |
| This journal is © The Royal Society of Chemistry 2015 |