Origin of the relaxation barriers in a family of MReIV(CN)2 single-chain magnets (M = MnII, NiII, and CoII): a theoretical investigation†
Yi-Quan
Zhang
* and
Cheng-Lin
Luo
Jiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, P. R. China. E-mail: zhangyiquan@njnu.edu.cn
First published on 28th October 2014
Abstract
Through investigation of the origin of the relaxation barriers and the magneto-structural correlations in three (DMF)4MReIVCl4(CN)2 (DMF = dimethylformamide; M = MnII (1), NiII (2), and CoII (3)) single-chain magnets (SCMs) in the intermediate regime between the Ising and the Heisenberg limits using hybrid functional theory (B3LYP) and complete active space second-order perturbation theory (CASPT2) methods, we succeeded in obtaining the magnetic anisotropy and correlation energy barriers ΔA and Δξ in terms of D (magnetic anisotropy parameter), J (magnetic exchange coupling constant), and S (spin value). B3LYP calculations show that the antiferromagnetic ReIV–MnII coupling interactions decrease with the increase of the Mn–N–C angle, while the ferromagnetic ReIV–NiII coupling interactions increase with the increase of the Ni–N–C angle. But, the ReIV–CoII exchange interactions with the variation of the Co–N–C angle are almost the same. The total energy barriers Δτ of 1 and 2 mainly come from the contribution of the transverse anisotropy of ReIV, while the MnII and NiII ions only transmit the exchange coupling between ReIV and almost have no contributions. For 3, however, both of the ReIV and CoII ions have contributions to the total energy barrier.
Introduction
For single-chain magnets (SCMs) when the anisotropy energy is not sufficiently higher than the exchange energy, they do not fall within the Ising limit with sharp domain walls and instead possess broad domain walls. In this intermediate regime between the Ising and the Heisenberg limits, the expressions of the magnetic anisotropy and correlation energy barriers ΔA and Δξ in terms of D (magnetic anisotropy parameter), J (magnetic exchange coupling constant), and S (spin value) were still not clear.1–3 Thus, exploring the expressions is vitally important, which will help us to understand the origin of the relaxation barriers so as to know how to increase them. Recently, Long and co-workers1 reported a series of (DMF)4MReIVCl4(CN)2 (DMF = dimethylformamide; M = MnII, NiII, CoII, and FeII) SCMs, and demonstrated that the correlation energy Δξ is far smaller than 4|JS1S2| since they do not fall within the Ising limit with sharp domain walls. Then, they used experimental methods to study the origin of the energy barrier for one of them, (DMF)4MnIIReIVCl4(CN)2, and demonstrated that the magnetic anisotropy energy barrier ΔA mainly comes from the contribution of the transverse anisotropy of ReIV.2 However, they did not give the expression of the correlation energy barrier Δξ, and also they did not investigate the other three complexes.2 In a recent work,3 we have done some research on one of them, R4FeIIReIVCl4(CN)2,1,4 and gave some interesting results. To probe the general rule, we will select the other three (DMF)4MReIVCl4(CN)2 (M = MnII (1), NiII (2), CoII (3)) SCMs which have much different magnetic properties from R4FeIIReIVCl4(CN)2 to explore the origin of the relaxation barriers and the expressions of ΔA and Δξ in terms of D, J, and S.Compared to the energy barriers and the intramolecular exchange interactions of R4FeIIReIVCl4(CN)2,1,4 those of the other three complexes MReIVCl4(CN)2 (M = MnII (1), NiII (2), CoII (3)) are so much different. The magnetic anisotropies of MnII and NiII in 1 and 2 are far smaller than those of FeII, and the ReIV–NiII and ReIV–CoII ferromagnetic interactions are weaker than those of ReIV–FeII. Moreover, the total energy barrier of 1 is far smaller than those of FeIIReIV although the ReIV–MnII exchange interactions are close to those of ReIV–FeII. Besides, the total energy barriers of 2 and 3 are very close although the magnetic anisotropies of NiII and CoII are so much different. To investigate the above problems, hybrid functional theory (B3LYP) and complete active space second-order perturbation theory (CASPT2) methods were performed to explore the origin of the energy barriers. Considering the similar structures of 1–3, we only gave the general structure in Fig. 1. They added a solution of M(ClO4)2 (M = MnII (1), NiII (2), CoII (3)) in 1.5 mL of DMF to a solution of (Bu4N)2[trans-ReCl4(CN)2] in 1.5 mL of DMF, which was allowed to stand for 8 hours to 12 days, to obtain the three complexes. A detailed description of the experimental details and the molecular structures can be found in ref. 1.
Computational details
The spin Hamiltonian of three MReIVCl4(CN)2 SCMs in the absence of spin–orbit coupling (SOC) is expressed as: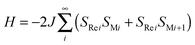 | (1) |
Orca 2.9.1 calculations5 using the popular hybrid functional B3LYP proposed by Becke6,7 and Lee et al.8 were performed to obtain the isotropic exchange coupling constant J. Triple-ζ with one polarization function TZVP9 basis set was used for all atoms, and the scalar relativistic treatment (ZORA) was used in all calculations. The large integration grid (grid = 6) was applied to ReIV and M (M = MnII, CoII, NiII) for ZORA calculations. Tight convergence criteria were selected to ensure that the results are well-converged with respect to technical parameters. We employed two model structures of A and B (see Fig. 2(a) and (b)) for each complex, and calculated two high- and one low-spin state energy for each model: SHS = SM1 + SRe + SM2 for model A; SHS = SRe1 + SM + SRe2 for model B, SLS = SM1 − SRe + SM2 with the flipped spins of ReIV for model A; SLS = SRe1 − SM + SRe2 with the flipped spins of M for model B. The HS state is a “real” state corresponding to the pure high spin state. But, the LS state is a spin contaminated state not a pure low spin state. The ReIV–M coupling constants J were then obtained as eqn (2)–(4) according to the spin Hamiltonian H = −2JSRe(SM1 + SM2) for model A and H = −2JSM(SRe1 + SRe2) for model B using the spin-projected approach.10
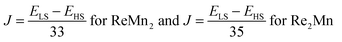 | (2) |
 | (3) |
 | (4) |
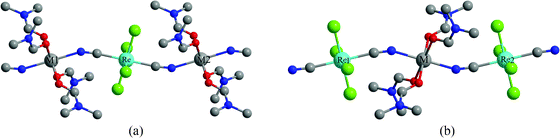 | ||
| Fig. 2 Structures of models A (DMF)4M[ReIVCl4(CN)2]2 (a) and B [(DMF)4MCN]2ReIVCl4(CN)2 (b); H atoms are neglected for clarity. | ||
Since density functional theory (DFT) methods in the calculation of D and E are not accurate enough to describe the magnetic anisotropies for our investigated systems,3,11 MOLCAS 7.8 program package12 with CASPT2 was used to calculate the D and E values of the ReIV (ReIVCl4(CN)2Zn2) and M [M(DMF)4(CN)2Ba2] fragments extracted from each complex. To calculate the ReIV fragment (see Fig. 3(a)), the influence of the neighboring M ions have been simulated by the closed-shell ZnIIab initio embedding model potentials (AIMP; Zn.ECP.Lopez-Moraza.0s.0s.0e-AIMP-KZnF3).13 The only removed atoms are those connected to the ZnII AIMP from the opposite side of the molecule. Similarly, the neighboring ReIV ions have been simulated by the closed-shell BaII AIMP (Ba.ECP.Pascual.0s.0s.0e-AIMP-BaF2)13 for each M fragment (Fig. 3(b)).
 | ||
| Fig. 3 Calculated ReIV (ReIVCl4(CN)2Zn2) (a) and M [M(DMF)4(CN)2Ba2] (b) fragments; H atoms are neglected for clarity. | ||
The basis sets for all atoms are atomic natural orbitals from the MOLCAS ANO-RCC library: ANO-RCC-VTZP for magnetic center ions ReIV and M; VTZ for close C and N; VDZ for distant atoms in the first complete-active-space self-consistent field (CASSCF) calculations. The scalar relativistic contractions were taken into account in the basis set. After that, the effect of the dynamical electronic correlation was applied using CASPT2. And then, the SOC was handled separately in the restricted active space state interaction (RASSI) procedure. The active space is (3,5), (5,5), (8,10), and (7,10) for the ReIV, MnII, NiII and CoII fragments, respectively. The mixed spin-free states are 40, 100, 25, and 50 for the ReIV, MnII, NiII, and CoII fragments, respectively.
Results and discussion
Exchange coupling interactions
The calculated and experimental J values of three (DMF)4MReIVCl4(CN)2 are shown in Table 1, where the ReIV–MnII couplings of 1 are antiferromagnetic, but those of 2–4 are ferromagnetic.For 1–4, both of the calculated J values of models A and B for each complex are close to the experimental one. Moreover, the obtained J values using model B may be better in the calculations of J for all complexes.
To explore the mechanism of the ReIV–M exchange couplings, we gave three magnetic orbitals localized on ReIV(t2g3) and five on MnII(t2g3eg2) of 1 in Fig. 4 in the low-spin state (the magnetic orbitals on ReIV, NiII and CoII of 2–3 can be found in Fig. S1 and S2 in the ESI†).
For 1, the antiferromagnetic interactions dominate over the competing ferromagnetic interactions between ReIV(t2g3) and MnII(t2g3eg2) centers due to one more t2g unpaired electron of MnII results in the antiferromagnetic ReIV–MnII coupling. It is evident that the ReIV–NiII coupling in 2 is ferromagnetic for the orthogonal magnetic orbitals on ReIV(t2g3) and NiII(eg2) metals (see Fig. S1 in the ESI†). For 3, the CoII(t2g1eg2) center houses one less unpaired electron in a π-type orbital, which leads to the ReIV–CoII ferromagnetic interactions (see Fig. S2 in the ESI†).
To thoroughly investigate the relationship between J and the M–N–C angle for the investigated three SCMs, we calculated J with the M–N–C angle changing from 140° to 180° using model B (see Fig. 2(b)) for 1–3, respectively. The obtained J values of 1–3 with the M–N–C angle ranging from 140° to 180° are shown in Table 2.
| 140° | 145° | 150° | 155° | 160° | 165° | 170° | 175° | 180° | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | −9.9 | −8.3 | −7.4 | −6.7 | −6.1 | −5.5 | −5.8 | −5.7 | −4.9 |
| 2 | 2.3 | 2.9 | 3.2 | 4.7 | 5.9 | 6.7 | 6.9 | 7.2 | 8.6 |
| 3 | −1.9 | 0.5 | 2.2 | 3.7 | 4.6 | 5.0 | 5.1 | 5.0 | 4.9 |
According to Kahn's theory,14 the square of the mean overlap integral Sij between magnetic orbitals on the paramagnetic centers i and j, which favors the antiferromagnetic contribution JAF, can be correlated to the Δij for polynuclear complexes proposed by Ruiz and co-workers.15
 | (5) |
The variation of J can be correlated with the changes in the JAF term, which usually control the magneto-structural correlations.16 The spin populations on ReIV and M were obtained using Mulliken Population Analysis17 calculated using the B3LYP functional. The strength of the JAF is linearly dependent on Δij.14
| |JAF| ∝ Sij2 ∝ Δij | (6) |
Fig. 5 gives the relationship between Δij and the M–N–C angle ranging from 140° to 180° for 1–3, respectively.
For 1, the decrease of the Δij with the Mn–N–C angle ranging from 140° to 180° leads to the decrease of the absolute values of Sij, and to the decrease of the JAF term. Thus, the antiferromagnetic ReIV–MnII coupling constant J (J = JF + JAF) decrease with the increase of the Mn–N–C angle. The decrease of the Δij with the increase of the Ni–N–C angle leads to the decrease of the absolute values of Sij, and to the decrease of the JAF term, which will strengthen the ferromagnetic ReIV–NiII coupling in 2. For 3, however, the variation of the Δij with the Co–N–C angle ranging from 140° to 180° is small, which results in the small differences in the ReIV–CoII coupling constants.
Expressions of the anisotropy and correlation energy barriers
CASPT2 could give the most accurate D values for complexes [ReIVCl4(CN)2]2−,1,2 (DMF)4ZnReCl4(CN)2,2 [TPA2C(O)NHtBuFeII(CF3SO3)]+ (TPA2C(O)NHtBu = 6,6′-(pyridin-2-ylmethylazanediyl)bis(methylene)-bis(N-tert-butylpicolinamide))18 and (TPA2C(O)NHtBu)FeIIReIVCl4(CN)219 compared to those calculated by DFT and CASSCF methods.3 For other transition metal systems containing MnII, NiII, and CoII ions, CASPT2 also performs well in the calculations of D.11,20 Thus, in the following calculations, CASPT2 will be used.For one-dimensional systems falling within the Ising limit, Δξ can be expressed as 4|JS1S2|. In the cases of 1–3, however, the experimental Δξ values are all far smaller than 4JSReSM.1 It is evident that 1–3 do not fall within the Ising limit. To explore the constitution of the domain walls and the expressions of Δξ and ΔA in terms of D, J and S, we firstly calculated the Di and Ei values of the ReIV (ReIVCl4(CN)2Zn2) and M ((DMF)4M(CN)2Ba2) fragments extracted from three SCMs (see Fig. 3), respectively, which are shown in Table 3.
| 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|
| ReIV | MnII | ReIV | NiII | ReIV | CoII | |
| D i | 11.3 | −0.29 | 16.7 | −2.9 | 19.5 | −5.6 |
| E i | −1.91 | −0.11 | −2.30 | −0.73 | −2.03 | −0.86 |
| (Di − Ei)/J | 0.15 | 0.59 | 1.97 | |||
| 2|Ei|/J | 0.71 | 1.24 | 1.69 | |||
| J | −5.4 | 3.7 | 2.4 | |||
As we know, when all Di/J values are larger than 4/3 in one SCM for homo-spin chains with collinear anisotropy axes, sharp domain walls are present with a creation energy given by Δξ = 4|J|S1S2.21 For our investigated hetero-spin MReIV(CN)2 SCMs, assuming that the anisotropy axes on ReIV and M are parallel, we deduced that when Di/J is larger than 2.5 for ReIV and 5/6 for MnII of 1, 1 for ReIV and 2 for NiII of 2, 1.5 for both of ReIV and CoII of 3, sharp domain walls are present according to Barbara and co-workers' theory (ΔA > 1/3Δξ).22 Since the rhombic anisotropy of M will shortcut the energy barrier, we simply use Di − Ei to replace Di to define the ratio (Di − Ei)/J. For ReIV in three SCMs, however, their D values are all positive. Thus, we use 2|Ei|/J to define the ratio for the ReIV fragments (for an easy-plane system, the anisotropy energy associated with the reversal of a single ReIV spin within a chain is given by ΔA = 2|E|S2 (E = (Dx − Dy)/2)).2
From the 2|Ei|/J and (Di − Ei)/J values of ReIV and M in Table 3, three SCMs have different conditions. For 1, the 2|Ei|/J and (Di − Ei)/J values of ReIV and MnII are smaller than 2.5 and 5/6, respectively. For 2, the 2|Ei|/J of ReIV is larger than 1, while the (Di − Ei)/J of NiII is smaller than 2. For 3, however, both 2|Ei|/J and (Di − Ei)/J values of ReIV and CoII are larger than 1.5. To explore the origin of the magnetic anisotropies, we firstly gave the general easy plane and axis on the ReIV and M fragments of 1–3 in Fig. 6.
 | ||
| Fig. 6 Alignment of the local easy plane and hard axis on the ReIV (ReIVCl4(CN)2Zn2), and the local easy axis on the M ((DMF)4M(CN)2Ba2) fragments of 1–3. | ||
In three MReIV(CN)2 SCMs, the easy planes on ReIV or the easy axes on M are strictly parallel. Fig. 6 shows that the easy axes on M do not lie in the easy planes on ReIV for three SCMs. The included angles between the easy axes on M and the hard axes on ReIV for 1–3 are 62.2°, 65.6° and 67.1°, respectively.
For 1, due to the very small magnetic anisotropy energy barrier of MnII, it can be approximately regarded as an isotropic ion, and so the spins on MnII will be orientated to the direction of the spins on ReIV under the strong ReIV–MnII antiferromagnetic coupling interactions. When the spins on one ReIV begin to flip, the spins on the neighboring MnII flip simultaneously, and those of ReIV on the other side also flip following them due to its small (Di − Ei)/J value. When the spins of ReIV on the other side start to flip, the exchange interaction on the left ReIV from the central MnII is the largest (see Fig. 7).
 | ||
| Fig. 7 Alignment of the spins on one ReIV (left or front), the central MnII, and the other ReIV (right or behind) when the spins on the other ReIV begin to flip. | ||
At this moment, the spins on the central MnII, the other neighboring ReIV and the spins on the left ReIV have the directions shown in Fig. 7 (the weak next neighboring exchange interactions are omitted). When the ΔA/Δξ of the right ReIV is smaller than 1/3, the spins on it begin to flip. Thus, we deduced that when the included angle between the spins on the right ReIV and the central MnII is close to 64.1°, the spins on the right ReIV start to flip (due to the mixing of the magnetic anisotropy combined with the strong exchange coupling for ReIV, it has much more quantum states than the normal spin states). In conclusion, the total energy barrier Δτ of 1 is closely equal to the creation energy of flipping the spins on one ReIV, which needs to overcome the anisotropic energy barrier ΔA, 2|E|S2, and the correlation energy barrier Δξ coming from the exchange interaction on the left ReIV from the central MnII, which is about 2JSReSMn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 − cos
0 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64.1) (64.1° is the included angle between the spins on the right ReIV and the central MnII when the spins on the right ReIV start to flip). The calculated and experimental ΔA, Δξ and Δτ values are shown in Table 4.
64.1) (64.1° is the included angle between the spins on the right ReIV and the central MnII when the spins on the right ReIV start to flip). The calculated and experimental ΔA, Δξ and Δτ values are shown in Table 4.
Since one domain wall contains more than one unit cell of ReIVCl4(CN)2(DMF)4 due to its 2|Ei|/J being much smaller than 2.5, the ΔA obtained only from the fragment of ReIV is inappropriate. Thus, the calculated ΔA of 1 is smaller than the experimental one in Table 4. The calculated Δξ is a little larger than the experimental one since the weak exchange interaction from the next neighboring MnII on the central MnII is omitted by us. The apparently better Δτ value results from the error cancellation in the calculations of the ΔA and Δξ. Considering the complex of the constitution of the domain wall, further work should be done to explore it thoroughly.
For 2, one unit cell of ReIVCl4(CN)2(DMF)4 can be regarded as a domain wall since its 2|Ei|/J value is larger than 1, while the (Di − Ei)/J value of NiII is far smaller than 2. When the spins on one ReIV were flipped by 180°, the ones on the neighboring NiII will not be of the same direction to those of ReIV due to the exchange interaction from the other side ReIV. Thus, the spins on the central NiII will be orientated to the direction perpendicular to its original one under the competing interactions of the two neighboring ReIV around NiII when the spins on one ReIV were completely flipped to the opposite direction (see Fig. 8).
 | ||
| Fig. 8 Alignment of the spins on one ReIV (left or front), the central NiII, and the other ReIV (right or behind) when the spins on the left or front ReIV completely flip to the opposite direction. | ||
Different from 1, the spins on the right ReIV of 2 will remain still when the spins on the left ReIV were completely flipped to the opposite direction since its 2|Ei|/J value is larger than 1. Thus, the total energy barrier Δτ of 2 is closely equal to the sum of the magnetic anisotropy energy barrier of one ReIV, 2|E|S2, and the correlation energy barrier Δξ, which is closely equal to half of 4JSReSNi (see Fig. 8). The calculated and experimental ΔA, Δξ and Δτ of 2 are shown in Table 5.
From Table 5, the calculated ΔA is a little smaller than that of the experiment since the weak contribution of the NiII is omitted, while the calculated Δξ is a little larger because the weak next neighboring NiII–NiII exchange coupling is not considered. Thus, the obtained Δτ is fortunately close to the experimental one.
For 3, since the 2|Ei|/J and (Di − Ei)/J values of ReIV and CoII in Table 3 are all larger than 1.5, it can be regarded as a spin-canted system. Considering the nonparallel magnetic axes on ReIV and M for 3, the criterion ratio ΔA/Δξ should be smaller than 1.5. Thus, it is further confirmed that 3 can be closely regarded as a spin-canted system. The alignment of the local ground magnetic axes on the ReIV (ReIVCl4(CN)2Zn2) and CoII (CoIIR(CN)2Ba2) fragments was shown in Fig. 9.
 | ||
| Fig. 9 Alignment of the local ground magnetic axes on the ReIV (ReIVCl4(CN)2Zn2) and CoII (CoIIR(CN)2Ba2) fragments. | ||
For the ReIV fragment, the ground spins were orientated to the direction of the gx axis since its D is positive and E is negative. Thus, the included angle θ of the ground spins on the ReIV and CoII of 3 is 63.1°, and so the calculated Δξ = 4JSReSCo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63.1 (using the experimental J value) is 9.8 cm−1, which is close to the experimental value (see Table 6).
63.1 (using the experimental J value) is 9.8 cm−1, which is close to the experimental value (see Table 6).
From Table 6, the magnetic anisotropy energy barriers ΔA of ReIV and CoII are 8.1 cm−1 and 9.5 cm−1, respectively, both of which are close to the experimental one. A little larger ΔA of CoII is due to the overestimated magnetic anisotropy energy barrier of CoII using 2|D|, which is usually larger than the effective energy barrier for the mixing of the ground and excited levels.23 Moreover, the calculated Δξ is a little larger since 3 could not be completely regarded as a spin-canted system for the D of CoII and the E of ReIV being not far larger than J (D ≫ J and E ≫ J).
Contrary to the FeIIReIV(CN)2 SCM,1,3 the total energy barriers Δτ of 1 and 2 mainly come from the contribution of the transverse anisotropy of ReIV, while the MnII and NiII ions only transmit the exchange couplings between ReIV and almost have no contributions. For 3, however, both of ReIV and CoII ions have contributions to the total energy barrier.
Conclusions
Hybrid functional and complete active space second-order perturbation theory were used to explore the origin of the relaxation barriers and the Δξ and ΔA in terms of D, J, and S in a series of MReIV(CN)2 single-chain magnets. Calculations show that the antiferromagnetic ReIV–MnII coupling interactions decrease with the increase of the Mn–N–C angle, while the ferromagnetic ReIV–NiII coupling interactions increase with the increase of the Ni–N–C angle. However, the variation of the ReIV–CoII exchange interactions with the Co–N–C angle ranging from 140° to 180° is very small.The 2|Ei|/J and (Di − Ei)/J values of ReIV and M of three complexes in Table 3 are so much different. For 1, the total energy barrier Δτ is closely equal to the creation energy of flipping the spins on one ReIV, which needs to overcome the anisotropic energy barrier ΔA, 2|E|S2, and the correlation energy barrier Δξ coming from the exchange interaction on the left ReIV from the central MnII, which is about 2JSReSMn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 − cos
0 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64.1). For 2, the total energy barrier Δτ is closely equal to the sum of the magnetic anisotropy energy barrier of one ReIV, 2|E|S2, and the correlation energy barrier Δξ, 2JSReSNi. For 3, it can be approximately regarded as a spin-canted system, and thus the Δξ is equal to 4JSReSCocos
64.1). For 2, the total energy barrier Δτ is closely equal to the sum of the magnetic anisotropy energy barrier of one ReIV, 2|E|S2, and the correlation energy barrier Δξ, 2JSReSNi. For 3, it can be approximately regarded as a spin-canted system, and thus the Δξ is equal to 4JSReSCocos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63.1 and the ΔA is equal to the magnetic anisotropy energy barrier of one ReIV or CoII.
63.1 and the ΔA is equal to the magnetic anisotropy energy barrier of one ReIV or CoII.
The above results show that simply enhancing the ReIV–M coupling is not always effective to increase the total energy barriers of MReIV(CN)2. To obtain the high energy barrier for single-chain magnets, we must enhance the magnetic anisotropy energy barriers of single magnetic ions and the intramolecular coupling at the same time.
Acknowledgements
This project is funded by the Natural Science Foundation of Jiangsu Province of China (BK2011778), and the Priority Academic Program Development of Jiangsu Higher Education Institutions.References
- T. D. Harris, M. V. Bennett, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2010, 132, 3980 CrossRef CAS PubMed.
- X. W. Feng, J. J. Liu, D. Harris, S. Hill and J. R. Long, J. Am. Chem. Soc., 2012, 134, 7521 CrossRef CAS PubMed.
- Y. Q. Zhang, C. L. Luo, X. B. Wu, B. W. Wang and S. Gao, Inorg. Chem., 2014, 53, 3503 CrossRef CAS PubMed.
- X. W. Feng, T. D. Harris and J. R. Long, Chem. Sci., 2011, 2, 1688 RSC.
- F. Neese, ORCA–An Ab Initio, Density Functional and Semiempirical Program Package, Version 2.9.1, Max Planck Institute for Bioinorganic Chemistry, Mülheim an der Ruhr, Germany, 2012 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- (a) A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef PubMed; (b) A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef PubMed.
- (a) L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS PubMed; (b) L. Noodleman and E. J. Baerends, J. Am. Chem. Soc., 1984, 106, 2316 CrossRef CAS; (c) L. Noodleman and D. A. Case, Adv. Inorg. Chem., 1992, 38, 423 CrossRef CAS.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741 CrossRef CAS PubMed.
- G. Karlstr€om, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222 CrossRef.
- L. Seijo and Z. Barandiarán, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszcynski, World Scientific, Singapore, 1999, vol. 4, pp. 55–152 Search PubMed.
- (a) O. Kahn and B. J. Briat, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 268 RSC; (b) J. J. Girerd, Y. Journaux and O. Kahn, Chem. Phys. Lett., 1981, 82, 534 CrossRef CAS.
- (a) T. Cauchy, E. Ruiz and S. Alvarez, J. Am. Chem. Soc., 2006, 128, 15722 CrossRef CAS PubMed; (b) J. Cano, R. Costa, S. Alvarez and E. Ruiz, J. Chem. Theory Comput., 2007, 3, 782 CrossRef CAS.
- O. Kahn, Molecular Magnetism, VCH, New York, 1993 Search PubMed.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, McGraw-Hill, New York, 1989 Search PubMed.
- H. S. Soo, M. T. Sougrati, F. Grandjean, G. J. Long and C. J. Chang, Inorg. Chim. Acta, 2011, 369, 82 CrossRef CAS PubMed.
- T. D. Harris, H. S. Soo, C. J. Chang and J. R. Long, Inorg. Chim. Acta, 2011, 369, 91 CrossRef CAS PubMed.
- C. Duboc, D. Ganyushin, K. Sivalingam, M.-N. Collomb and F. Neese, J. Phys. Chem. A, 2010, 114, 10750 CrossRef CAS PubMed.
- C. Coulon, H. Miyasaka and R. Clerac, Struct. Bonding, 2006, 122, 163 CrossRef CAS.
- B. Barbara, J. Magn. Magn. Mater., 1994, 129, 79 CrossRef CAS.
- (a) E. Ruiz, J. Cano, S. Awarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS; (b) E. Ruiz, S. Alvarez, J. Cano and V. Polo, J. Chem. Phys., 2005, 123, 164110 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nj01491j |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2015 |



