Searching beyond Gd for magnetocaloric frameworks: magnetic properties and interactions of the Ln(HCO2)3 series†
Paul J.
Saines
*a,
Joseph A. M.
Paddison
ab,
Peter M. M.
Thygesen
a and
Matthew G.
Tucker
b
aDepartment of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford, OX1 3QR, UK. E-mail: paul.saines@chem.ox.ac.uk
bISIS Facility, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX1 3QR, UK
First published on 21st July 2015
Abstract
This study probes the magnetic properties and interactions of the Ln(HCO2)3 (Ln = Tb3+–Er3+) frameworks. We show that the magnetocaloric effect of Tb(HCO2)3 is significantly higher above 4 K in moderate magnetic fields compared to the promising Gd(HCO2)3. While the peak performance of Tb(HCO2)3 is lower than Gd(HCO2)3, we also find that the Gd-rich members of the solid solution Gd1−xTbx(HCO2)3 blend the advantages of both end-members. Using neutron diffraction experiments, Tb(HCO2)3 is found to be antiferromagnetic below 1.7 K with ferromagnetic face-sharing chains and antiferromagnetic coupling between them. Analysis of magnetic diffuse scattering of the paramagnetic phase indicates that ferromagnetic coupling is retained, and it is likely that this plays a role in improving its magnetocaloric performance in low fields.
Conceptual insightsAlternate coolants are needed to replace the use of increasingly scarce liquid helium to reach ultra-low temperatures, required, for example, to cool superconductors used in medical resonance imaging to below 10 K. Paramagnetic magnetocalorics, which posses entropically driven cooling when in a cycled magnetic field, are one such replacement. Recently gadolinium-based coordination frameworks that have amongst the largest magnetocaloric effects have been developed; the cooling power of these materials, however, peaks below 2 K, below the temperatures required for many applications of liquid helium. This work shows that the incorporation of heavier lanthanides, in particular terbium, into a magnetocaloric framework can lead to a significant increase in their performance at higher temperatures—particularly in applied fields reachable using permanent magnets, the most practical for functional cooling devices. The detailed magnetic interactions in terbium formate have also been examined, the first study of the magnetic correlations in a paramagnetic coordination framework, which reveals that Ising-like one-dimensional ferromagnetic coupling is present in the paramagnetic phase. These interactions are likely to play a role in its excellent magnetocaloric performance by increasing its ease of magnetisation. |
1. Introduction
Functional magnets have great potential to underpin the development of new technologies for a wide range of applications.1,2 Coordination frameworks have attracted particular attention in this regard, because their unusual architectures allow them to exhibit uniquely-modified magnetic properties not found in conventional ionic solids.2–4 Recently, frameworks have been created that exhibit the paramagnetic magnetocaloric effect (MCE),2,5,6 an entropically-driven cooling process that occurs when paramagnets are in a cycled magnetic field. Several frameworks, including Gd(HCO2)3, have recently been reported whose MCEs are comparable or superior to Gd3Ga5O12, the benchmark compound for MCE cooling below 10 K.5,6 These materials have possible applications as ultra-low-temperature coolants, potentially replacing increasingly expensive and scarce liquid helium.2,7 The current focus of the development of MCE frameworks lies in achieving higher maximum entropy changes – typically for temperatures below 2 K and applied magnetic fields greater than 5 T. Such materials are used as a second stage in an adiabatic demagnetisation refrigerator (ADR), with liquid helium or a cryocooler, cooling the system down to 4 K before magnetic cooling enables the sample environment to be cooled below 1 K, typically for scientific observation. Given the increasing scarcity of liquid helium and complexity and reliability issues of multistage cryocoolers, which are necessary to reach 4 K, the development of magnetocaloric compounds that operate more efficiently at moderately higher temperatures may be useful when combined with a single stage cryocooler capable of reaching 10–20 K.8 Ideally, this would be accompanied by having as large an MCE as possible in lower applied fields, particularly below the typical 2 T field limits of permanent magnets.5,9 This could allow more economical devices to be created for many applications requiring cooling in the 4–10 K range, e.g. cooling the niobium superconducting magnets used in medical resonance imaging and nuclear magnetic resonance facilities.10Very little is known regarding how the paramagnetic interactions in magnetocalorics relate to their fascinating properties. Neutron scattering is the method of choice for probing magnetic interactions and has recently begun to be applied to study magnetically-ordered frameworks;4,11 its application, however, to magnetocalorics and other low dimensional and frustrated frameworks is very limited.12 This is because sufficiently large single crystals of coordination frameworks are seldom available, and it has long been considered that little information about the paramagnetic state can be extracted using neutron powder diffraction. While the very large neutron-absorption cross section of Gd also typically restricts studying many magnetocalorics, recent studies have shown that this problem is surmountable.13 Our research on frustrated and disordered magnets has shown that significantly more information can be obtained from powder magnetic diffuse scattering than has traditionally been anticipated.14,15 Applying such techniques to frameworks would enable a much deeper understanding of their low dimensional or frustrated behaviour.
Here we present a survey of the magnetic properties of the Ln(HCO2)3 (Ln = Tb3+, Dy3+, Ho3+ and Er3+) frameworks. Unexpectedly, we reveal that Tb(HCO2)3 has a larger MCE than Gd(HCO2)3 for temperatures between 4 and 10 K and applied fields below 2 T. Doping across the Gd1−xTbx(HCO2)3 solid solution series is found to further optimize the MCE properties of this family. Encouraged by the properties of Tb(HCO2)3, we also investigated its magnetic interactions using neutron diffraction, characterising both its long-range magnetic order present below 1.7 K and the short-range order in its paramagnetic phase—the first time that such a study has been completed on a coordination framework. We show that ferromagnetic coupling within the TbO9 chains in Tb(HCO2)3 is the dominant interaction in the paramagnetic phase, which may play a role in its interesting magnetocaloric properties.
2. Experimental
Samples were synthesised by slowly adding 1 g of the appropriate Ln(NO3)3·xH2O (99.9%, x = 6 for Ln = Gd3+ or Tb3+, Sigma-Aldrich, and x = 5 for Ln = Dy3+, Ho3+ and Er3+, Alfa Aesar) to 5 mL of formic acid (Sigma-Aldrich, 95% reagent grade) in a 30 mL tall glass vial. This was stirred overnight and the product filtered off, washing with ethanol. Gd1−xTbx(HCO2)3 was made by reactions carried out with finely ground stoichiometric mixtures of Gd(NO3)3 and Tb(NO3)3. The 5 g sample of Tb(DCO2)3 used for neutron diffraction was made using the same method but was a combination of three batches made using 4 g of Tb(NO3)3·6H2O and perdeuterated formic acid (Sigma-Aldrich 95% in D2O, 98% D). Sample purity was examined by powder X-ray diffraction, using a Bragg–Brentano PANalytical Empyrean diffractometer equipped with Cu-Kα1 radiation and a PIXcel detector. Dc magnetisation data were collected using a Quantum Design MPMS 5 XL SQUID magnetometer with powder samples contained in gel caps and held in a straw with a uniform diamagnetic background.Time-of-flight neutron powder diffraction patterns were recorded using the GEM diffractometer at the ISIS neutron facility, Rutherford Appleton Laboratories, UK.16 Data covered a reciprocal-space range 0.25 < Q < 25 Å−1 and were measured at temperatures between 1.4 K and 300 K for 30 μAh (900 μAh at 3 K). The sample was cooled in an 8 mm V can in an Oxford Instruments Variox Cryostat. Data were fitted using the GSAS Rietveld refinement package using the EXPGUI interface.17 Refinements were carried out with a profile function featuring a convolution of back-to-back exponentials with a pseudo-Voigt model, with backgrounds fitted using shifted Chebyschev polynomials. Refinement of the D fractional occupancy showed that the sample is perdeuterated.
Likely magnetic structures for the ordered phase were determined using the ISODISTORT software suite18 by exploring the magnetic distortion modes and symmetries consistent with the observed magnetic propagation vector, k, and the parent crystal structure. In order to characterise short-range spin correlations in the paramagnetic state, magnetic diffuse scattering data were obtained from the lowest-Q detector bank (bank 1) on GEM. Bragg scattering, as determined from Rietveld refinements, and experimentally measured background contributions, including from the sample environment, were subtracted. The resulting magnetic diffuse-scattering data were fitted using the Spinvert Reverse Monte Carlo (RMC) refinement package.15 In RMC refinement, spin orientations in a periodic supercell are fitted to diffuse-scattering data using a Metropolis Monte Carlo algorithm. We used a 5 × 3 × 13 size metrically-orthorhombic supercell related to the trigonal cell by a basis vector of [(1, 0, 0),(1/3, 2/3, 0),(0, 0, 1)]. The magnetic form factor of Tb3+ was obtained from tabulated coefficients.19 The phase scale and a flat background term were also refined.
3. Results and discussion
3.1 Magnetic properties of the Ln(HCO2)3 frameworks
Rietveld fits to X-ray diffraction data confirmed that all samples used in this study were phase pure and adopt the known rhombohedral R3m structure under ambient conditions (see Fig. S1–S5, ESI†).5 In this structure the LnO9 polyhedra are connected into face-sharing chains down the c-axis with these chains interconnected via the formate ligand into a triangular arrangement (see Fig. 1). There are two different oxygen cations in the structure, bonding to one and two Ln3+ cations, respectively, with the latter anion connecting the Ln3+ cations in a chain. The triangle connections of the Ln3+ cation are not equilateral but instead feature two short bonds and one long bond, which rotate between adjacent layers along the c-axis.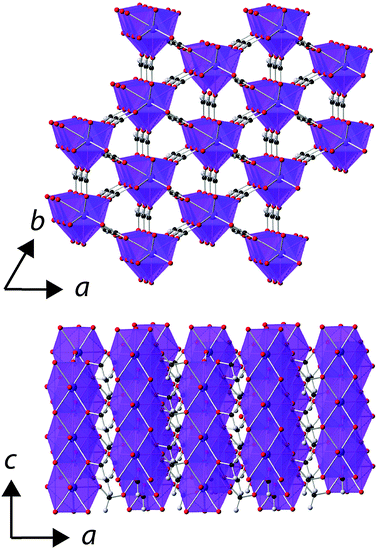 | ||
| Fig. 1 The structure of the Ln(HCO2)3 frameworks. The Ln3+, oxygen, carbon and hydrogen atoms are represented in purple, red, black and grey, respectively. | ||
Field cooled (FC) and zero-field cooled (ZFC) magnetic susceptibility data of the Ln(HCO2)3 frameworks (Ln = Gd3+, Tb3+, Dy3+, Ho3+ and Er3+) were measured in a 100 Oe field from 2 K to 300 K and did not show any indication of long range magnetic order. These data were well fitted using the Curie–Weiss law (see Fig. S6–S10, ESI†) with Curie–Weiss temperatures of −0.6 K, −0.9 K, −6.1 K, −10.3 K and −16.0 K, for Gd3+–Er3+. Gd(HCO2)3, therefore, has antiferromagnetic interactions but the significant orbital moment of the other lanthanides means their Curie–Weiss temperatures are a sum of any magnetic interactions and the effect of depopulation of the Stark levels so a similar analysis cannot be made. Effective magnetic moments were found to be broadly consistent with the values expected for these trivalent lanthanides according to the Russell–Saunders coupling scheme, with values of 7.86, 9.62, 10.00, 10.48 and 9.68 μB obtained. Magnetisation measurements exhibit paramagnetic behaviour and appear close to saturation under an applied field of 5 T (see Fig. S11–S16, ESI†). Interestingly, Tb(HCO2)3 appears close to saturation at 1 T, a much lower field than its Gd3+ analogue despite its higher magnetic anisotropy (discussed below); this greater ease of magnetisation increases further with increasing temperature.
Magnetic entropy change, ΔSm, was calculated from the Maxwell relation 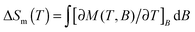 from 2 K to 12 K for ΔB = 5–0 T. This gave −ΔSmaxm of 15.7, 20.8, 14.7 and 19.2 J kg−1 K−1 for Tb3+, Dy3+, Ho3+ and Er3+, with Tmax of 7, 6, 4 and 2 K, corresponding to volumetric values of −ΔSmaxm of 61.3, 82.9, 60.1 and 79.1 mJ cm−3 K−1 (see Fig. S17, ESI†). These −ΔSm values are all significantly lower than the 190.4 mJ cm−3 K−1 we obtain for Gd(HCO2)3 with Tmax = 2 K for ΔB = 5–0 T, which is close to the value found in a previous study.5 The higher Tmax temperatures of the other lanthanides, particularly Tb3+, attracted our attention. Indeed, for ΔB = 1–0 T the −ΔSm of Tb(HCO2)3 is significantly higher than that of Gd(HCO2)3 above 4 K. The same is true for Ho(HCO2)3, albeit to a very small extent (see Fig. 2a). A greater −ΔSm is also observed for Tb(HCO2)3 for ΔB = 2–0 T above 6 K, although the differences in the values achieved compared to the Gd3+ compound are smaller (see Fig. 2b). This result highlights that the incorporation of Tb3+ cations into coordination frameworks allows their MCE properties to be optimised at higher temperatures and in lower applied fields, compared to the corresponding Gd3+ compound. Previous studies of Gd1−xTbxGa5O12 showed the same effect, but by a much smaller margin.20 This is significant as many of the applications of liquid helium do not require cooling below 4 K, which most paramagnetic MCE materials are optimised for. It should be noted here that the magnetocaloric effect can be probed directly from heat capacity measurements, which is desirable particularly when determining the specific heat transfer, ΔQ.21 Recent work on Gd(HCO2)3 and GdOH(CO3), however, have shown that for similar frameworks excellent agreement is usually obtained between the direct determination of −ΔSm and the indirect method presented in this work.
from 2 K to 12 K for ΔB = 5–0 T. This gave −ΔSmaxm of 15.7, 20.8, 14.7 and 19.2 J kg−1 K−1 for Tb3+, Dy3+, Ho3+ and Er3+, with Tmax of 7, 6, 4 and 2 K, corresponding to volumetric values of −ΔSmaxm of 61.3, 82.9, 60.1 and 79.1 mJ cm−3 K−1 (see Fig. S17, ESI†). These −ΔSm values are all significantly lower than the 190.4 mJ cm−3 K−1 we obtain for Gd(HCO2)3 with Tmax = 2 K for ΔB = 5–0 T, which is close to the value found in a previous study.5 The higher Tmax temperatures of the other lanthanides, particularly Tb3+, attracted our attention. Indeed, for ΔB = 1–0 T the −ΔSm of Tb(HCO2)3 is significantly higher than that of Gd(HCO2)3 above 4 K. The same is true for Ho(HCO2)3, albeit to a very small extent (see Fig. 2a). A greater −ΔSm is also observed for Tb(HCO2)3 for ΔB = 2–0 T above 6 K, although the differences in the values achieved compared to the Gd3+ compound are smaller (see Fig. 2b). This result highlights that the incorporation of Tb3+ cations into coordination frameworks allows their MCE properties to be optimised at higher temperatures and in lower applied fields, compared to the corresponding Gd3+ compound. Previous studies of Gd1−xTbxGa5O12 showed the same effect, but by a much smaller margin.20 This is significant as many of the applications of liquid helium do not require cooling below 4 K, which most paramagnetic MCE materials are optimised for. It should be noted here that the magnetocaloric effect can be probed directly from heat capacity measurements, which is desirable particularly when determining the specific heat transfer, ΔQ.21 Recent work on Gd(HCO2)3 and GdOH(CO3), however, have shown that for similar frameworks excellent agreement is usually obtained between the direct determination of −ΔSm and the indirect method presented in this work.
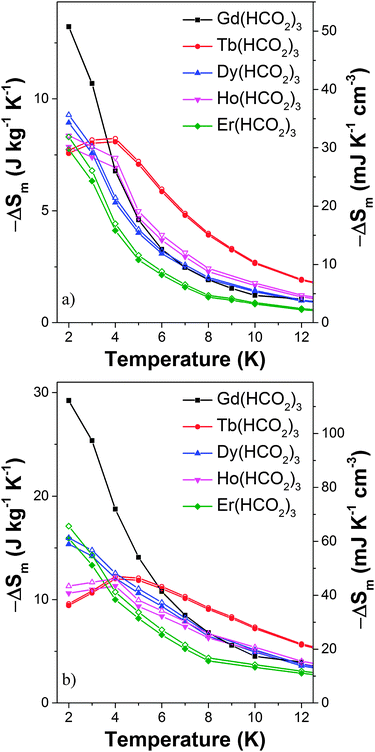 | ||
| Fig. 2 Magnetic entropy change for the Ln(HCO2)3 frameworks for (a) ΔB = 1–0 T and (b) ΔB = 2–0 T. The filled and hollow symbols mark mass and volumetric units, respectively. | ||
Since the incorporation of Tb3+ yielded improved MCE properties at higher temperatures compared to Gd(HCO2)3 but lower −ΔSmaxm, the magnetic properties of the Gd1−xTbx(HCO2)3 (x = 0.2, 0.4, 0.6 and 0.8) solid solution were investigated. High-resolution X-ray diffraction indicate these compounds are pure single phases, although there was some evidence of peak broadening, suggesting that they exhibit a degree of strain or cation inhomogeneity (see Fig. S18, ESI†). Magnetic susceptibilities were well fitted by Curie–Weiss law, yielding effective magnetic moments consistent with stoichiometries of x = 0.19, 0.40, 0.57 and 0.76 across the series, close to the expected nominal stoichiometries. The Curie–Weiss temperatures were −0.9 K for the whole series except for Gd0.4Tb0.6(HCO2)3, which had a value of −1.3 K. Only Gd0.4Tb0.6(HCO2)3 varied from mean-field behaviour, with an antiferromagnetic cusp present in ZFC measurements at 3 K that is not observed in FC data (see Fig. S19, ESI†); magnetization measurements at 2 K are consistent with paramagnetic behaviour suggesting Gd0.4Tb0.6(HCO2)3 is not a simple antiferromagnet.
For the x = 0.2 and 0.4 members of the Gd1−xTbx(HCO2)3 series the −ΔSm for ΔB = 1–0 T are significantly higher than would be expected for a physical mix of the two end-member phases. This is particularly significant for Gd0.8Tb0.2(HCO2)3 as at 2 K, the lowest temperature probed its −ΔSm for a ΔB = 1–0 T is equal to that of Gd(HCO2)3. It decreases more slowly than for the pure Gd phase, such that for temperatures above 5 K its −ΔSm is between 10–15% higher (see Fig. 3 and Fig. S20–S23 for magnetisation data, ESI†). Similarly, while the −ΔSmaxm for Gd0.6Tb0.4(HCO2)3 is about 10% lower than Gd(HCO2)3 for a ΔB = 1–0 T above 5 K, its −ΔSm is between 14 to 24% higher. The performance of both doped compounds also exceeds that of Gd(HCO2)3 at higher temperatures for a ΔB = 2–0 T, although this is only above 6 and 7 K for x = 0.2 and x = 0.4, respectively, and the difference remains less than 10%. To the best of our knowledge this is the first study of the magnetocaloric properties of a framework solid solution and has shown the potential advantages of such an approach to optimise the physical properties of such materials – namely, retaining most of the performance of Gd(HCO2)3 in low fields, while improving on its MCE at moderately higher temperatures.
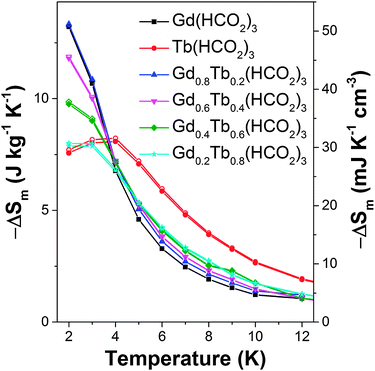 | ||
| Fig. 3 Magnetic entropy change for the Gd1−xTbx(HCO2)3 series for ΔB = 1–0 T. The filled and hollow symbols mark mass and volumetric units, respectively. | ||
3.2 Magneto-structural characterisation of Tb(DCO2)3
The interesting properties of Tb(HCO2)3 encouraged further investigation of its structure and magnetic interactions using neutron diffraction, particularly in the paramagnetic phase. Past studies of the Ln(HCO2)3 frameworks have suggested a subtle structural transition occurs below 150 K due to a very small reduction (≈0.05%) of the c-axis in Tm(DCO2)322 and features observed in Raman spectra of Pr(HCO2)3.23 The proposed transition is from the ambient temperature R3m rhombohedral structure to R3 symmetry and involves a rotation of the formate groups.23 Neutron diffraction should be particularly sensitive to such a transition, as it will involve a significant movement of the deuterium atoms. We find a similar minute change in the lattice parameters of Tb(DCO2)3 below 80 K (see Fig. S24, ESI†), but Rietveld refinements to the data collected at 3 K using both possible space groups give equivalent excellent fits: for R3, Rp = 1.60% and Rwp = 2.26%, and for R3m, Rp = 1.67% and Rwp = 2.30%. Moreover, the maximum displacement of each atom in the R3 structure is within 0.1 Å of the position required by R3m symmetry. We therefore conclude that R3m symmetry is retained to 3 K (see Tables S1–S4 for crystallographic details and selected bond distances and angles determined at 3 and 300 K, ESI†). There are no significant changes observed that indicate the cause of the subtle change in the c-axis length. There is also no indication of diffuse scattering appearing above 10 K, so it is unlikely to be related to structural disorder.A neutron diffraction pattern obtained from Tb(DCO2)3 at 1.4 K revealed the presence of additional reflections, especially at high d-spacing (see Fig. 4), consistent with the emergence of magnetic order. These were found to index on the parent cell but violated the rhombohedral centering conditions. This is consistent with the magnetic structure of Tb(DCO2)3 belonging to the k-vector Λ, (0, 0, g), which is allowed to be incommensurate but here appears to have locked into a commensurate value of g = 1. Of the possible magnetic structures suggested by ISODISTORT only those belonging to the magnetic space group P3m′1 fitted the data. There were two possible magnetic structures of this type, each of which have ferromagnetic face-sharing chains, with spins found to align along the c-axis. One possible structure has three ferromagnetic chains with one chain having twice the magnetic moment of the others and coupled antiferromagnetically to them (see Fig. 5a). This model is consistent with that proposed in a previous study of Kurbakov et al.,24 who briefly analysed the magnetic structure of Tb(DCO2)3 using a basis vector approach. The other structure has the spins in two ferromagnetic chains coupled antiferromagnetically to each other with the remaining chain being disordered (see Fig. 5b), a so-called spin-idle structure. The fits of these two structures to the 1.4 K data are equivalent (Rp = 1.94% for both models and Rwp = 2.09% and 2.10% for the spin-idle and unequal spin structure, respectively). The largest magnetic moment is 5.91 μB and 6.80 μB for the spin-idle and unequal-spin structure, respectively. These values are well below the expected magnetic moment of 9.72 μB for isotropic Tb3+ moments, consistent with the observation of magnetic diffuse scattering, which persists more weakly up to 10 K. Magnetic reflections appear between 1.65 and 1.72 K, indicating the onset of magnetic order (see Fig. S25 for the evolution of the magnetic moments, ESI†). The square of the observed magnetic moment is proportional to the Landau order parameter, Q; a good linear fit to the square of the ordered magnetic moment is obtained, confirming that the magnetic-ordering transition is second order and occurs at 1.72(12) K.
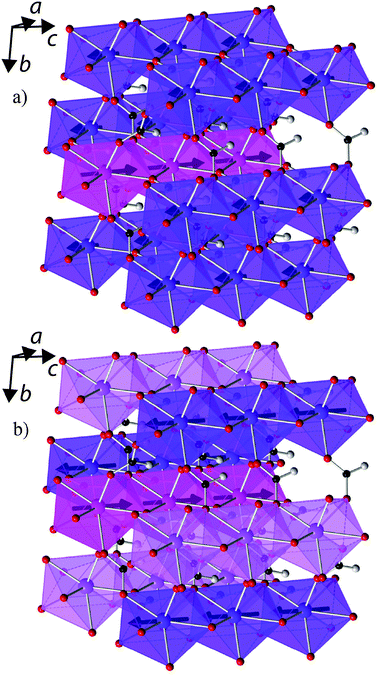 | ||
| Fig. 5 The two possible magnetic structures of Tb(DCO2)3. The distinct Tb3+ cations are shown in different colours with the ordered spin direction indicated by the arrows pointing through them. All other colours are the same as in Fig. 1. | ||
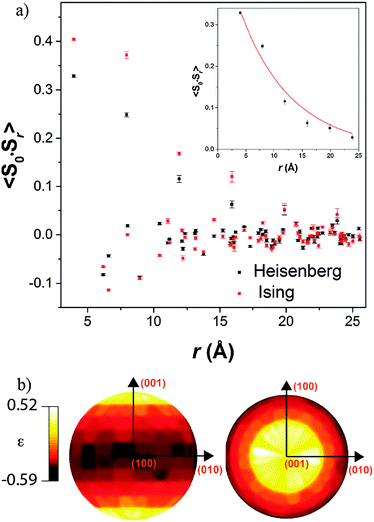
Both possible magnetic structures of Tb(DCO2)3 indicate that the dominant intra-chain coupling is ferromagnetic, consistent with the small Tb–O2–Tb bond angle of 105.79(4)°. As the intra-chain super-exchange distances are much smaller than those between chains (cf. 4.98 Å to 7.42 Å), it would be expected that this compound will resemble a one-dimensional system above its long-range ordering temperature. Fits to the diffuse magnetic scattering observed at 3 K using RMC refinement confirm that this is the case (see Fig. 6 for the quality of fit). Initially, unconstrained refinements were performed in which the spins were allowed to point in any direction, in a Heisenberg-like fashion. A plot of 〈S0·Sr〉 averaged over ten such refinements show that the dominant spin correlations in this material are ferromagnetic within the chains (see Fig. 7a), with a correlation length of 9.2(1.3) Å. The inter-chain correlations are much weaker and antiferromagnetic, with 〈S0·Sr〉 correlations of −0.082(2) and −0.044(3) observed for Tb3+ cations separated by the shorter, 6.16 Å and longer, 6.57 Å distances found in the triangles, respectively.
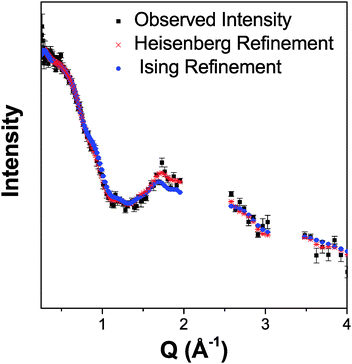 | ||
| Fig. 6 Comparison of the Heisenberg-like and Ising-like RMC fits to the neutron diffuse scattering of Tb(DCO2)3 at 3 K. The results are averaged over ten refinements. | ||
Stereographic projections of the refined spin orientations indicate that even well above the magnetic ordering temperatures the spins are preferentially aligned along the c-axis (see Fig. 7b), indicating an Ising-like magnetic anisotropy. Attempts were therefore made to fit the diffuse scattering data with Ising spins constrained to point along the c-axis. The Ising refinements also yielded a reasonable fit, though of somewhat lower quality than the unconstrained refinement (cf. χ2 of 290 and 414 for ten averaged Heisenberg and Ising fits, respectively), which would be expected as the Ising refinement is more highly constrained. This result suggests that the spins have a strong, although probably not purely, Ising character. To the best of our knowledge this is the first RMC study of the magnetic interactions in the paramagnetic phase of a coordination framework.
The significant ferromagnetic intra-chain interactions in the paramagnetic phase of Tb(HCO2)3 explain the relative ease of its magnetization compared to Gd(HCO2)3, whose negative Curie–Weiss temperature indicates predominantly antiferromagnetic interactions. It can be envisaged that the strong ferromagnetic intra-chain interactions, present on a local scale of about 10 Å, will lead to the Tb3+ spins aligning readily with an applied magnetic field, easily overcoming the much weaker inter-chain antiferromagnetic coupling. Bulk measurements show that this greater ease of magnetization is retained to higher temperature, leading to a higher peak temperature for −ΔSmaxm than found in Gd(HCO2)3, which may make Tb(HCO2)3 suitable for cooling applications at moderately higher temperatures. The trade-off for this is a lower −ΔSmaxm compared to Gd(HCO2)3, due to a combination of its lower magnetic moment and a more gradual change of magnetisation with temperature. In the Gd1−xTbx(HCO2)3 solid solution a mixture of these two cations leads to a retention of most of the peak performance of the Gd(HCO2)3 but a slower reduction in −ΔSm with temperature in low applied fields. While to date the development of magnetocaloric frameworks has focused on Gd3+ containing-compounds, this study highlights the benefits of incorporating heavier lanthanides into framework structures known to have excellent magnetocaloric properties. By combining a deeper understanding of their magnetic interactions with judicious choices of doping in solid solutions, it should be possible to expand the palate of available magnetocaloric frameworks and optimize their application.
4. Conclusion
In this work we have reported the MCE of the Ln(HCO2)3 (Ln = Tb3+, Dy3+, Ho3+ and Er3+) frameworks for the first time and compared them to the properties of the related Gd(HCO2)3, which is already proven to be an excellent candidate as a magnetocaloric material.5 We have shown that, although the peak performance of the other lanthanide formates is not as great as for Gd(HCO2)3, the temperature at which their performance peaks is significantly higher. This is particularly important in the case of the Tb3+ compound, which significantly outperforms Gd(HCO2)3 above 4 K in fields below 2 T, the maximum field typically achievable with permanent magnets. Moreover, we show that the Gd3+-rich end-members of the solid solution Gd1−xTbx(HCO2)3 retain much or all of the peak performance of Gd(HCO2)3 but also exhibit a slower decline in their −ΔSm, leading to better performance. The magnetic order of Tb(DCO2)3 in both its antiferromagnetic and paramagnetic phases has also been examined. We find that the Tb3+ spins in the edge-sharing chains order ferromagnetically below 1.7 K into an arrangement featuring antiferromagnetic triangles. Only partial order occurs, indicating the inherent frustration in this system, and significant magnetic diffuse scattering therefore remains. Fitting magnetic diffuse scattering in the paramagnetic phase, suggests that the compound resembles a one-dimensional ferromagnetic chain with magnetic moments oriented along the c-axis as in the ordered phase, which increases its ease of magnetisation and thereby magnetocaloric properties.Acknowledgements
Experiments at the ISIS Pulsed Neutron Source were supported by a beamtime allocation from the Science and Technology Facilities Council. PJS would like to thank the Glasstone Bequest for financial support through the provision of a Glasstone Fellowship and Professor Andrew Goodwin for helpful discussions.References
- (a) J. Glanz, Science, 1998, 279, 2045 CrossRef CAS; (b) G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and J. D. Cashion, Science, 2002, 298, 1762–1765 CrossRef CAS PubMed; (c) D. Maspoch, D. Ruiz-Molina, K. Wurst, N. Domingo, M. Cavallini, F. Biscarini, J. Tejada, C. Rovira and J. Veciana, Nat. Mater., 2003, 2, 190–195 CrossRef CAS PubMed; (d) W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759–765 CrossRef CAS PubMed.
- Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475 RSC.
- (a) M. Kurmoo, H. Kumagai, K. W. Chapman and C. J. Kepert, Chem. Commun., 2005, 3012–3014 RSC; (b) M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379 RSC; (c) G. Rogez, N. Viart and M. Drillon, Angew. Chem., Int. Ed., 2010, 49, 1921–1923 CrossRef CAS PubMed; (d) Z. Wang, K. Hu, S. Gao and H. Kobayashi, Adv. Mater., 2010, 22, 1526–1533 CrossRef CAS PubMed; (e) P. J. Saines, M. Steinmann, J.-C. Tan, W. Li, P. T. Barton and A. K. Cheetham, Inorg. Chem., 2012, 51, 11198–11209 CrossRef CAS PubMed; (f) P. J. Saines, P. T. Barton, P. Jain and A. K. Cheetham, CrystEngComm, 2012, 14, 2711–2720 RSC.
- P. J. Saines, P. T. Barton, M. Jura, K. S. Knight and A. K. Cheetham, Mater. Horiz., 2014, 1, 332–337 RSC.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656 CrossRef CAS PubMed.
- (a) S. Biswas, H. S. Jena, A. Adhikary and S. Konar, Inorg. Chem., 2014, 53, 3926–3928 CrossRef CAS PubMed; (b) Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendac, J. Prokleska, V. Sechovsky and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858 RSC; (c) Y. Meng, Y.-C. Chen, Z.-M. Zhang, Z.-J. Lin and M.-L. Tong, Inorg. Chem., 2014, 53, 9052–9057 CrossRef CAS PubMed.
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672–4676 RSC.
- (a) Z. H. Gan, W. Q. Dong, L. M. Qiu, X. B. Zhang, H. Sun, Y. L. He and R. Radebaugh, Cryogenics, 2009, 49, 198–201 CrossRef CAS PubMed; (b) L. Chen, H. Jin, J. Wang, Y. Zhou, W. Zhu and Q. Zhou, Cryogenics, 2013, 54, 54–58 CrossRef CAS PubMed; (c) K. Yamada, Cryogenics, 2014, 63, 110–113 CrossRef CAS PubMed.
- (a) K. A. GschneidnerJr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef; (b) A. Smith, C. R. H. Bahl, R. Bjørk, K. Engelbrecht, K. K. Nielsen and N. Pryds, Adv. Energy Mater., 2012, 2, 1288–1318 CrossRef CAS PubMed.
- L. Yuri, S. Ernst Wolfgang and Z. Tao, Supercond. Sci. Technol., 2013, 26, 093001 CrossRef.
- (a) P. J. Saines, J. R. Hester and A. K. Cheetham, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144435 CrossRef; (b) O. Fabelo, L. Cañadillas-Delgado, I. Puente Orench, J. A. Rodríguez-Velamazán, J. Campo and J. Rodríguez-Carvajal, Inorg. Chem., 2011, 50, 7129–7135 CrossRef CAS PubMed; (c) P. J. Saines, H. H. M. Yeung, J. R. Hester, A. R. Lennie and A. K. Cheetham, Dalton Trans., 2011, 40, 6401–6410 RSC; (d) L. Cañadillas-Delgado, O. Fabelo, J. A. Rodríguez-Velamazán, M.-H. Lemée-Cailleau, S. A. Mason, E. Pardo, F. Lloret, J.-P. Zhao, X.-H. Bu, V. Simonet, C. V. Colin and J. Rodríguez-Carvajal, J. Am. Chem. Soc., 2012, 134, 19772–19781 CrossRef PubMed; (e) R. A. Mole, M. A. Nadeem, J. A. Stride, V. K. Peterson and P. T. Wood, Inorg. Chem., 2013, 52, 13462–13468 CrossRef CAS PubMed; (f) J. M. M. Lawler, P. Manuel, A. L. Thompson and P. J. Saines, Dalton Trans., 2015, 44, 11613–11620 RSC.
- A. Kumar, S. M. Yusuf, L. Keller, J. V. Yakhmi, J. K. Srivastava and P. L. Paulose, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224419 CrossRef.
- (a) O. A. Petrenko, C. Ritter, M. Yethiraj and D. McK Paul, Phys. Rev. Lett., 1998, 80, 4570–4573 CrossRef CAS; (b) E. Reynolds, P. E. R. Blanchard, B. J. Kennedy, C. D. Ling, S. Liu, M. Avdeev, Z. Zhang, G. J. Cuello, A. Tadich and L.-Y. Jang, Inorg. Chem., 2013, 52, 8409–8415 CrossRef CAS PubMed; (c) E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423 CrossRef.
- (a) A. M. Hallas, J. A. M. Paddison, H. J. Silverstein, A. L. Goodwin, J. R. Stewart, A. R. Wildes, J. G. Cheng, J. S. Zhou, J. B. Goodenough, E. S. Choi, G. Ehlers, J. S. Gardner, C. R. Wiebe and H. D. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134431 CrossRef; (b) J. A. M. Paddison and A. L. Goodwin, Phys. Rev. Lett., 2012, 108, 017204 CrossRef; (c) P. J. Saines, M. G. Tucker, D. A. Keen, A. K. Cheetham and A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 134418 CrossRef; (d) J. A. M. Paddison, S. Agrestini, M. R. Lees, C. L. Fleck, P. P. Deen, A. L. Goodwin, J. R. Stewart and O. A. Petrenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 014411 CrossRef.
- J. A. M. Paddison, J. R. Stewart and A. L. Goodwin, J. Phys.: Condens. Matter, 2013, 25, 454220 CrossRef PubMed.
- A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88–107 CrossRef CAS PubMed.
- B. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS.
- P. J. Brown, Magnetic Form Factors, http://www.ill.eu/sites/ccsl/ffacts/ffachtml.html, 2015.
- C. P. Reshmi, S. Savitha Pillai, K. G. Suresh and M. R. Varma, J. Magn. Magn. Mater., 2012, 324, 1962–1966 CrossRef CAS PubMed.
- V. Khovaylo, J. Alloys Compd., 2013, 577, S362–S366 CrossRef CAS PubMed.
- V. Trounov, E. Tserkovnaya, S. Gavrilov and S. Vahrushev, Physica B, 1997, 234–236, 679–681 CrossRef CAS.
- M. R. Moura, A. P. Ayala, J. Mendes Filho, I. Guedes, C. W. A. Paschoal, A. G. Leyva, G. Polla, D. Vega, P. K. de Perazzo and H. Lanza, J. Raman Spectrosc., 2004, 35, 159–164 CrossRef CAS PubMed.
- A. I. Kurbakov, J. Rodriguez-Carvajal, V. Trounov and N. V. Starostina, Mater. Sci. Forum, 2000, 321–324, 971–975 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mh00113g |
| This journal is © The Royal Society of Chemistry 2015 |

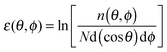
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)