 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the energy levels in hole-doped molecular semiconductors†
Stefanie
Winkler
ab,
Patrick
Amsalem
a,
Johannes
Frisch
a,
Martin
Oehzelt
ab,
Georg
Heimel
*a and
Norbert
Koch
*ab
aInstitut für Physik & IRIS Adlershof, Humboldt-Universität zu Berlin, Brook-Taylor-Straße 6, D-12489 Berlin, Germany. E-mail: georg.heimel@physik.hu-berlin.de; norbert.koch@physik.hu-berlin.de
bHelmholtz-Zentrum Berlin für Materialien und Energie GmbH, Bereich Enerneuerbare Energien, D-12489 Berlin, Germany
First published on 18th May 2015
Abstract
Understanding the nature of polarons – the fundamental charge carriers in molecular semiconductors – is indispensable for rational material design that targets superior (opto-) electronic device functionality. The traditionally conceived picture of the corresponding energy levels invokes singly occupied molecular states within the energy gap of the semiconductor. Here, by employing a combined theoretical and multi-technique experimental approach, we show that this picture needs to be revised. Upon introducing an excess electron or hole into the material, the respective frontier molecular level is split by strong on-site Coulomb repulsion into an upper unoccupied and a lower occupied sub-level, only one of which is located within the semiconductor gap. By including also inter-site Coulomb interaction between molecular ions and circumjacent neutral molecules, we provide a complete picture for the electronic structure of molecular semiconductors in the presence of excess charges. With this understanding, a critical re-examination of previous results is called for, and future investigations of the properties and dynamics of polarons in weakly interacting molecular systems are put on sound footing.
Conceptual insightsThe importance of molecular semiconductors in emerging information and display technologies is progressively increasing. A key element of bringing these technologies to the next level is an improved control over charge carrier, i.e., polaron, properties. The nature of these polarons, excess charges strongly coupled to structural degrees of freedom, must be fully understood to achieve this control. The traditional picture of polarons established in the organic electronics community has not been critically questioned since the early 1980's, despite the fact that the photoelectron spectra obtained on molecular semiconductors comprising polarons were frequently at odds with this model. We now show that this traditional model, which predicts singly occupied molecular levels within the energy gap of the semiconductor, needs to be revised. For molecular ions, the respective frontier molecular level is split by strong on-site Coulomb repulsion into an upper unoccupied and a lower occupied sub-level, only one of which lies within the semiconductor gap. By including also inter-site Coulomb interaction between molecular ions and surrounding neutral molecules, we provide a complete picture for the photoelectron spectral signature of the energy levels in hole- and electron-doped molecular semiconductors. Our results call for a re-interpretation of many previous reports, and will enable a deeper understanding of charge carriers in these complex systems in the future. |
Molecular semiconductors are progressively employed in electronic and optoelectronic devices because of the wide tunability of their optical gap, e.g., in organic light-emitting diodes (OLEDs), their high light absorption cross section, e.g., in organic photovoltaic cells (OPVCs), and also their potential for low-cost large-area processability from solution, e.g., by printing. At the same time, however, the performance of such devices often suffers from the relatively low charge carrier mobility in molecular semiconductors compared to their inorganic counterparts. To address this critical issue, it is of paramount importance to understand in detail the nature of charge carriers (excess electrons and holes) in these materials, where strong coupling of both electrons and holes to (inter- and intra-) molecular vibrations leads to polaron formation.1–6
For a positively charged molecule, that is, for a cation, in a matrix of neutral molecules, Fig. 1(a) shows the relevant single-particle energy levels and their occupation according to the commonly accepted and widely used picture.2,3,7–14 Removing an electron from the highest occupied molecular orbital (HOMO) level of a neutral molecule leads to its geometrical relaxation and a concomitant shift by the reorganization energy λ of the now singly occupied state into the energy gap of the semiconductor.2 Concomitantly with this change of energy levels also the optical transitions of cations change with respect to neutral molecules (usually sub-gap absorption), which, however, are not discussed here.
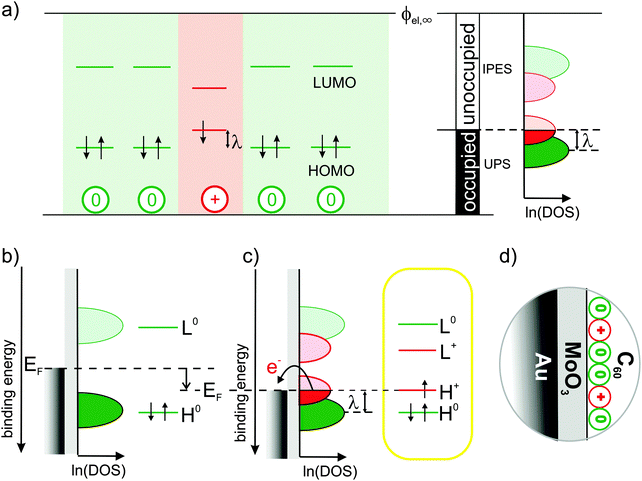 | ||
Fig. 1 Traditional view of the molecular single-particle energy levels and how they can be created and measured: (a) single-particle energy levels for neutral molecules (green) surrounding a cation (red) with respect to a common vacuum level ϕel,∞, their experimental accessibility to (inverse) photoelectron spectroscopy depending on their occupancy and the resulting density of states (DOS) on a logarithmic scale, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (DOS), as proposed according to common assumptions in ref. 7. (b) Single-particle energy level diagrams for a neutral molecule on an intermediate and (c) a high work-function substrate causing electron transfer that results in cations.2,3,7–10 The latter is realized here with the Au/MoO3/C60-heterostructure (d). (DOS), as proposed according to common assumptions in ref. 7. (b) Single-particle energy level diagrams for a neutral molecule on an intermediate and (c) a high work-function substrate causing electron transfer that results in cations.2,3,7–10 The latter is realized here with the Au/MoO3/C60-heterostructure (d). | ||
Based on this picture, it is widely anticipated7,10,11 that (i) the doubly occupied states should be experimentally accessible by ultraviolet photoelectron spectroscopy (UPS), (ii) the empty states by inverse photoelectron spectroscopy (IPES) and (iii) the singly occupied state by means of both UPS and IPES; these expectations for the density of states (DOS) in the molecular solid are illustrated in the right panel of Fig. 1(a) (adapted from ref. 7). Despite best efforts by means of UPS,9,15 however, clear spectral evidence for the relaxed cation's HOMO level within the gap is still missing.
Here, we seek to provide such evidence and realize that it is challenging even to generate the species of interest, i.e., molecular cations in a matrix of neutral but otherwise identical molecules: when generated by p-doping, the singly occupied state of the cation can hardly be distinguished from the filled lowest unoccupied molecular orbital (LUMO) level of the dopant9 and, moreover, strong electronic coupling between molecular HOMO and dopant LUMO cannot generally be excluded,16,17 which might significantly distort the DOS in the relevant energy range. Likewise, electronic coupling to atomically clean metal surfaces is known to not yield integer-charged molecules but to result in pronounced mixing of metal and molecular states instead.18,19
This hybridization with the metal, however, can be inhibited by inserting an insulator between metal and molecules, reminiscent of the situation in a p-type organic field-effect transistor (OFET) under applied (negative) gate voltage.20 Simplifying this approach, cations can be generated by employing a metal-supported, ultra-thin dielectric with a work function (WF) higher than the ionization energy (IE) of subsequently deposited molecules as depicted in Fig. 1(b) and (c). Thereby, the Fermi-level (EF) of the underlying metal is moved into the occupied DOS of the molecules, causing electron transfer from the molecules across the insulator into the metal to establish electronic equilibrium.
In the present study, this was realized with a 1.2 nm thin MoO3 layer (WF = 6.8 eV) supported by an atomically clean Au(111) single-crystal surface. To facilitate the detection of the potentially low cation concentrations, we employed C60 (IE = 6.4 eV) as hole accumulation layer due to its high orbital degeneracy (HOMO:5, LUMO:3); the full heterostructure is sketched in Fig. 1(d) (see also Methods section).
To confirm the presence of C60 cations, X-ray photoelectron spectroscopy (XPS) was first used to probe the C1s core-levels, which are known to be at different binding energy for the molecule in its neutral and cationic state.21Fig. 2(a) shows the C1s spectra for increasing C60 coverage, together with the results of the applied fitting procedure. The bottom curve in the figure shows that no carbon is adsorbed on the pristine MoO3. Upon C60 deposition, two distinct C1s peaks emerge, which are split by ∼0.7 eV and evidence the coexistence of cationic (high binding energy – red) and neutral (low binding energy – green) molecules at the interface. This literature-based assignment21 is also fully in line with the expectation of a decreasing fraction of charged molecules with increasing coverage in the monolayer regime,22,23 as the cation component becomes weaker compared to the neutral one with increasing coverage. Notably, the fraction of C60 cations is in the range of 40% below 1 Å nominal coverage (for other thicknesses see ESI†). From 1 Å nominal coverage onwards, a third C1s peak (blue) is required to maintain the quality of the fit. We attribute this additional component to neutral C60 molecules in a second layer, as illustrated in the inset of Fig. 2(c). While its presence is of no further consequence for the discussion below, it supports the notion of hole accumulation within the first layer, as it is energetically aligned according to the electrostatics of energy level bending (see ESI†).24–26
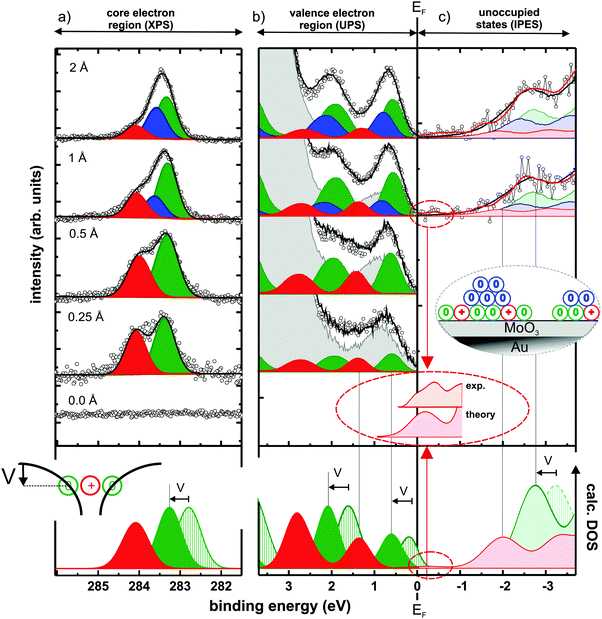 | ||
| Fig. 2 Spectra from photoemission and modelling of C60 layers comprising neutral molecules and radical cations: C60-coverage dependent (inverse) photoelectron spectra of (a) C1s core-levels, (b) occupied, and (c) unoccupied valence states. The experimental curves (black circles) can be reconstructed by a superposition (black line) of accordingly shifted and scaled thick-film C60 spectra for charged (red), neutral monolayer (green), and multilayer (blue) contributions with a background of bare MoO3/Au(111) (grey curve for UPS, see ESI† for unoccupied states). Inset in (c) illustrates the C60 growth mode. Bottom of (b) and (c) shows the DFT-calculated DOS of the neutral (green striped) and positively charged (red) molecules. Both were rigidly shifted in energy so that the occupied cation features match the experiment. To account for the Coulomb potential well created by nearby cations (inset of bottom panel), the calculated DOS of the neutral molecules is further shifted by V = 0.5 eV to higher binding energy. The magnification of the region close to EF highlights experimental and theoretical evidence for an unoccupied HOMO-derived state slightly above EF. | ||
Regarding the electrostatics within the hole-accumulating (sub)monolayer itself, it is important to note that, here, the neutral molecules observed in XPS reside within the Coulomb potential well created by nearby cations, as schematically sketched at the bottom of Fig. 2(a). Thereby, all energy levels of these neutral C60 molecules are shifted rigidly to higher binding energy (by an amount V). This ensures that their (fully occupied) HOMO levels now come to lie entirely below EF, thus preventing them from undergoing electron transfer to the underlying metal and, consequently, from becoming cations themselves. This process enables the coexistence of neutral and cationic molecules in the monolayer.23 The magnitude of V can be estimated by comparing the experimentally obtained core-level shift to that calculated by density functional theory (DFT) for a single C60 molecule in both its neutral and its charged state (see Methods section). Because calculations performed on single molecules cannot account for the mutual Coulomb interaction present in experiment, comparing the theoretically and experimentally obtained C1s binding energy differences of ∼1.2 eV and ∼0.7 eV, respectively, suggest V ≈ 0.5 eV.
Having confirmed the presence of C60 cations in the (sub)monolayer, we now turn to UPS to study its valence electronic structure, as shown in Fig. 2(b). With increasing coverage, molecular spectral features arise until, at about 30 Å (see ESI†), the typical thick-film spectrum of neutral C60 is obtained.27,28 For <1 Å coverage, however, subtraction of such a spectrum and the substrate contribution (each suitably scaled) inevitably yields a residual that resembles another C60 thick-film spectrum over a wide binding energy range (see ESI†). This implies the presence of a second, chemically intact, but energy-shifted C60 species as, in fact, expected from XPS. Indeed, the superposition of suitably scaled contributions from the substrate and two energetically shifted C60 spectra, one accounting for the neutral molecules and one for the cations, perfectly reconstructs the measured thin-film data, as depicted in Fig. 2(b). This spectral deconvolution is further justified by our DFT results, which confirm that the shape of the DOS is almost identical for neutral and cationic C60, as shown in the bottom of Fig. 2(b) and (c).
Because, as in XPS, the high binding energy spectral contribution decreases with increasing submonolayer coverage, the assignment of these two C60 species – also fully supported by DFT – has to be: the low binding energy component corresponds to neutral molecules (green) and the component at 0.8 eV higher binding energy corresponds to molecular cations (red). This is in clear contrast to the expectations outlined for UPS in Fig. 1(a) and (c).
To assess the validity of these expectations also for the unoccupied states, we applied the complementary spectroscopic technique IPES. The spectral intensity associated with C60 was retrieved by subtracting a suitably scaled substrate contribution from the raw data (see ESI†). Fig. 2(c) shows the obtained difference-spectra for increasing nominal film thickness, starting with a C60 coverage of 1 Å; for lower coverages the IPES intensity is insufficient due to the inherently low photon yield of the method. A superposition of three C60 contributions (one each for cations in the monolayer, neutral molecules in the monolayer, and neutral molecules in the second layer) with relative weights and energy offsets in accordance with both XPS and UPS satisfactorily reproduces the obtained IPES spectra.
More importantly, however, both experiment and theory reveal the presence of an unoccupied HOMO-derived state of the cation, attributed to one out of ten electrons missing in the fivefold degenerate HOMO of neutral C60 (see ESI† for a discussion of the reliability of this assertion and experimental details). This spectral feature is located close to and above EF (in IPES: −0.25 ± 0.25 eV binding energy) as deduced from the magnified comparison of calculated DOS and experimental spectrum in Fig. 2(c).
So, disconcertingly, the IPES results fulfil the expectations outlined in Fig. 1(a) and (c) while the UPS results are in strong contrast. To elucidate this striking discrepancy, we start out the discussion with Fig. 3(a): the energy required to remove an electron from a neutral molecule in the solid (IE0) via UPS equals the energy gain upon returning it onto the relaxed cation (EA+) via IPES plus the reorganization energy λ.4,29,30 Notably, the ionization energy IE+ of the cation, i.e., the second ionization energy of a neutral molecule, is higher than the first ionization energy IE0. This is related to the on-site Coulomb interaction between electrons in the HOMO, commonly referred to as Hubbard U,28,31,32 which we directly determined here to be U ≈ 1.4 eV (peak-to-peak split between the occupied and unoccupied HOMO-derived sublevels of the cation obtained by UPS and IPES, respectively) for a valence hole in solid C60. Accordingly, the upper unoccupied HOMO-derived sub-level of the cation is shifted by λ into the gap of the semiconductor and, thereby, comes to lie above the HOMO of the neutral molecules in energy. The lower occupied HOMO-derived sub-level appears at U–λ outside the gap of the semiconductor, that is, below the HOMO of the neutral molecules in energy. As shown in the center panel of Fig. 3(a), the energy levels of neutral molecules residing in the Coulomb potential well (ϕel,local) of the cation are shifted by (up to) V, a quantity that can now, in analogy to U, be related to the inter-site Coulomb interaction.33–35
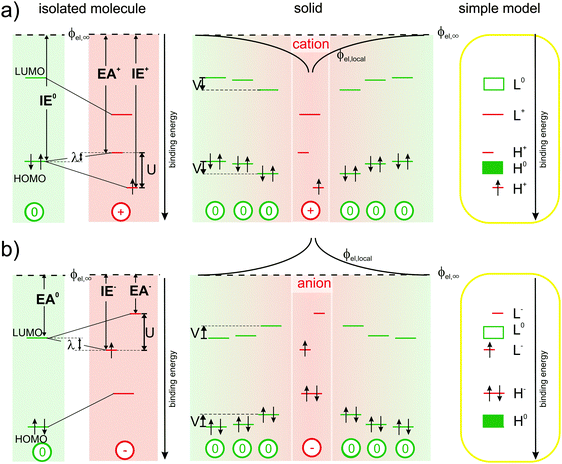 | ||
| Fig. 3 Revised energy levels in molecular semiconductors comprising polarons: (a) origin of the experimentally observable spectral signature of cations from left to right: the reorganization energy λ corresponds to the difference between IE0 and EA+. The on-site Coulomb-interaction U causes a splitting into two HOMO-derived sub-levels, EA+ and IE+ (with respect to a common vacuum level ϕel,∞), while inter-site Coulomb-interaction causes a distance dependent shift (ϕel,loc) by up to V of the energy levels of the neutral molecules in close vicinity of the cations. The right-most panel shows a simplified projection, correcting the traditional view outlined in Fig. 1(b). (b) Analogous to (a) for negative polarons. | ||
Based on these observations, we provide a simplified picture of the single-particle energy levels associated with cations in an otherwise neutral molecular film in the rightmost panel of Fig. 3(a), which we suggest should replace the hitherto followed one in Fig. 1(c).
In full analogy, Fig. 3(b) revises the picture for molecules carrying a negative polaron.2,3,10,11 The energy gained from adding an electron onto a neutral molecule in the solid (EA0) by IPES equals the ionization energy of the relaxed anion (IE−) minus the reorganization energy λ. The electron affinity of the anion (EA−), i.e., the second electron affinity of a neutral molecule, is now lower than the first electron affinity EA0. This is again caused by the on-site Coulomb-interaction between electrons in the LUMO. Therefore, the upper unoccupied LUMO-derived sub-level lies at U–λ outside the gap of the molecular semiconductor, and the lower occupied LUMO-derived sub-level is found to be shifted by λ into the gap of the semiconductor. The energy levels of neutral molecules within Couloumb-interaction range of nearby anions are shifted to lower binding energy by (up to) an amount V, which depends again on the distance to the anion. The emerging picture for the energy levels of anions in molecular solids, a simplified version of which is provided in the rightmost panel of Fig. 3(b), implies that literature-based expectations10,11 on their spectral signature should be revised as well.
To summarize, we started out with the quest of obtaining the photoelectron spectral signature of positively charged species in molecular semiconductors. To avoid potential masking of the expected signal by parasitic effects, we relied on electron transfer from the molecular HOMO across a thin, insulating interlayer to a metal substrate, thereby enabling the observation of “pure” cations in the first place.
Supported by DFT calculations, we assessed the energy shift of the single-particle levels in neutral molecules due to Coulomb-interaction with neighbouring cations to be V ≈ 0.5 eV. Naturally, the on-site Coulomb-interaction (Hubbard U) must exceed that value and was determined here, in a complementary UPS/IPES study, to amount to U ≈ 1.4 eV for the valence hole in C60. Most importantly, this term causes the ionization energy of cations to be substantially higher than that of the respective neutral molecules, necessitating a fundamental revision of the widely established picture of polarons in molecular semiconductors: instead of finding a single, singly occupied state within the gap of the neutral species, the respective frontier molecular orbital level (i.e., the HOMO for positive and the LUMO for negative polarons) is split by on-site Coulomb repulsion into an upper unoccupied sub-level and a lower occupied sub-level. For UPS and IPES this implies that the spectral intensity associated with charged molecules does not necessarily appear cut by EF. Consequently, such molecular films are not metallic as long as U dominates over weaker molecule–molecule and molecule–substrate interactions, which is often the case in the bulk or on passivated substrates.
Our suggestion of replacing the widely established picture of polarons might lead to new insights already from a re-interpretation of previous experimental results. More importantly, however, it might inspire new experiments on the fundamental properties of charge carriers in weakly interacting molecular systems, in particular, those induced by the electrical doping of molecular semiconductors through admixing strong electron donors or acceptors.
Methods
All samples were fabricated under ultra-high-vacuum conditions on an atomically clean Au(111) single crystal (MaTecK, repeated Ar+-ion-sputtering and annealing cycles up to 550 °C). MoO3 (density = 4.7 g cm−3) and C60 (density = 1.65 g cm−3) were purchased from Sigma Aldrich, purified via re-sublimation prior to use, and deposited from resistively heated crucibles. The evaporation rates (0.5–2 Å min−1) and the nominal film thicknesses were monitored using a quartz-crystal microbalance. The pressure during the evaporation did not exceed 5 × 10−8 mbar (preparation chamber) and samples were transferred to the interconnected analysis chamber (base pressure 3 × 10−10 mbar) without breaking the vacuum.To assess the electronic structure across the Au/MoO3/C60-heterostructures, in situ X-ray photoelectron spectroscopy (XPS: photon energy hν = 610 eV) and UPS (hν = 21 eV) spectra were collected at the end station SurICat (beamline PM4) of the synchrotron light source BESSY II (Berlin, Germany) using a hemispherical electron-energy analyser Scienta SES 100. IPES was performed in-house at HU-Berlin (incident electron energy range: 5–15 eV, NaCl-coated photocathode, SrF2-window).
Density-functional theory (DFT) calculations on isolated C60 molecules were performed with a hybrid exchange–correlation functional,36 mixing the generalized-gradient approximation developed by Perdew, Burke and Ernzerhof37 with a fraction α of Hartree–Fock (HF) exchange. In the spirit of ref. 38–40, α was determined by imposing Janak's theorem,41 that is, by requiring that the total-energy difference between neutral and positively charged molecule (at the neutral-molecule equilibrium structure) equals the eigenvalue of the highest occupied molecular orbital of neutral C60. To capture the screening of the excess hole on the fullerene by the environment (MoO3 and surrounding molecules), a polarizable continuum model42 with 3.5 as relative dielectric constant was employed. After repeatedly cycling through the determination of α and the geometry relaxation of the neutral molecule, an optimal value of α = 0.3147 finally emerged. The so-obtained hybrid-functional was then employed to relax the fullerene also to its (symmetry-broken) cation equilibrium geometry. All calculations were performed with Gaussian 09, Rev. A.0243 using the triple-ζ polarized 6-311G** contracted-Gaussian basis set44 for geometry optimization and one set of additional diffuse functions (6-311+G**) for single-point calculations.45
The core-level density of states (DOS) was obtained by broadening the entire manifold of C1s-related eigenvalues with area-normalized Gaussians of full-width at half-maximum (FWHM) of 0.7 eV. The valence DOS was produced by first broadening each valence-orbital eigenvalue with an area normalized Gaussian of standard deviation σ = 0.22 eV to emulate disorder, by subsequent multiplication with a room-temperature Fermi function (UPS) or one minus a Fermi function (IPES), and by finally convoluting the result with an area-normalized Gaussian of σ = 0.14 eV (UPS) or σ = 0.34 eV (IPES) to account for detector broadening. For the spin-polarized cations, possessing one more spin-up than spin-down electrons, two possible spin-multiplicities (singlet and triplet) in the final state of the UPS/IPES experiment were taken into account: removing a further spin-down electron from the cation by UPS (or adding another spin-up electron in IPES) results in one of three possible triplet states, while removing a spin-up electron by UPS (or adding a spin-down electron in IPES) result in a singlet final state. Therefore, the spin-down DOS for UPS (and the spin-up DOS in IPES) has been multiplied by a factor three before adding the spin-up DOS for UPS (and the spin-down DOS for IPES) to yield the final result displayed in Fig. 2 of the main text.
Acknowledgements
This work was supported by the DFG (SPP1355, SFB951, and AM419/1-1) and the Helmholtz-Energie-Allianz “Hybrid-Photovoltaik”. We further acknowledge Stefan Krause for help with the IPES-setup, Jürgen P. Rabe for providing access to the in-house multitechnique apparatus, Ruslan Ovsyannikov and Oliver Monti for support at BESSY.References
- M. Pope and C. E. Swenberg, Annu. Rev. Phys. Chem., 1984, 35, 613–655 CrossRef CAS.
- J. L. Bredas and G. B. Street, Acc. Chem. Res., 1985, 18, 309–315 CrossRef CAS.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS PubMed.
- E. A. Silinsh, A. Klimkāns, S. Larsson and V. Čápek, Chem. Phys., 1995, 198, 311–331 CrossRef CAS.
- N. Karl, Synth. Met., 2003, 133, 649–657 CrossRef.
- S. Kera, H. Yamane, I. Sakuragi, K. K. Okudaira and N. Ueno, Chem. Phys. Lett., 2002, 364, 93–98 CrossRef CAS.
- O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J. B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Nat. Mater., 2014, 13, 190–194 CrossRef CAS PubMed.
- M. Fahlman, A. Crispin, X. Crispin, S. K. M. Henze, M. P. de Jong, W. Osikowicz, C. Tengstedt and W. R. Salaneck, J. Phys.: Condens. Matter, 2007, 19, 183202 CrossRef CAS PubMed.
- W. Y. Gao and A. Kahn, J. Appl. Phys., 2003, 94, 359–366 CrossRef CAS PubMed.
- N. Koch, A. Rajagopal, J. Ghijsen, R. L. Johnson, G. Leising and J. J. Pireaux, J. Phys. Chem. B, 2000, 104, 1434–1438 CrossRef CAS.
- D. Steinmüller, M. G. Ramsey and F. P. Netzer, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13323–13329 CrossRef.
- M. Lögdlund, R. Lazzaroni, S. Stafström, W. R. Salaneck and J. L. Bredas, Phys. Rev. Lett., 1989, 63, 1841–1844 CrossRef.
- A. J. Heeger, Polym. J., 1985, 17, 201–208 CrossRef CAS.
- A. J. Heeger, S. Kivelson, J. R. Schrieffer and W. P. Su, Rev. Mod. Phys., 1988, 60, 781–850 CrossRef CAS.
- T. Sueyoshi, H. Fukagawa, M. Ono, S. Kera and N. Ueno, Appl. Phys. Lett., 2009, 95, 183303 CrossRef PubMed.
- I. Salzmann, G. Heimel, S. Duhm, M. Oehzelt, P. Pingel, B. M. George, A. Schnegg, K. Lips, R. P. Blum, A. Vollmer and N. Koch, Phys. Rev. Lett., 2012, 108, 035502 CrossRef.
- H. Mendez, G. Heimel, A. Opitz, K. Sauer, P. Barkowski, M. Oehzelt, J. Soeda, T. Okamoto, J. Takeya, J. B. Arlin, J. Y. Balandier, Y. Geerts, N. Koch and I. Salzmann, Angew. Chem., Int. Ed., 2013, 52, 7751–7755 CrossRef CAS PubMed.
- G. Heimel, S. Duhm, I. Salzmann, A. Gerlach, A. Strozecka, J. Niederhausen, C. Bürker, T. Hosokai, I. Fernandez-Torrente, G. Schulze, S. Winkler, A. Wilke, R. Schlesinger, J. Frisch, B. Bröker, A. Vollmer, B. Detlefs, J. Pflaum, S. Kera, K. J. Franke, N. Ueno, J. I. Pascual, F. Schreiber and N. Koch, Nat. Chem., 2013, 5, 187–194 CrossRef CAS PubMed.
- Y. Zou, L. Kilian, A. Schöll, T. Schmidt, R. Fink and E. Umbach, Surf. Sci., 2006, 600, 1240–1251 CrossRef CAS PubMed.
- S. L. Daifuku, C. Favaro, A. P. Marchetti and M. L. Neidig, Org. Electron., 2014, 15, 3761–3765 CrossRef CAS PubMed.
- C. D. Wagner, Handbook of X-ray photoelectron spectroscopy: a reference book of standard data for use in x-ray photoelectron spectroscopy, Physical Electronics Division, Perkin-Elmer Corporation, 1979 Search PubMed.
- B. J. Topham, M. Kumar and Z. G. Soos, Adv. Funct. Mater., 2011, 21, 1931–1940 CrossRef CAS PubMed.
- P. Amsalem, J. Niederhausen, A. Wilke, G. Heimel, R. Schlesinger, S. Winkler, A. Vollmer, J. P. Rabe and N. Koch, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035440 CrossRef.
- Irfan, M. L. Zhang, H. J. Ding, C. W. Tang and Y. L. Gao, Org. Electron., 2011, 12, 1588–1593 CrossRef CAS PubMed.
- H. B. Wang, P. Amsalem, G. Heimel, I. Salzmann, N. Koch and M. Oehzelt, Adv. Mater., 2014, 26, 925–930 CrossRef CAS PubMed.
- M. Oehzelt, N. Koch and G. Heimel, Nat. Commun., 2014, 5, 4174 CAS.
- J. H. Weaver, J. Phys. Chem. Solids, 1992, 53, 1433–1447 CrossRef CAS.
- R. Schwedhelm, L. Kipp, A. Dallmeyer and M. Skibowski, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 13176–13180 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- S. Kera, H. Yamane and N. Ueno, Prog. Surf. Sci., 2009, 84, 135–154 CrossRef CAS PubMed.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257 CrossRef.
- B. Alvarez-Fernandez and J. A. Blanco, Eur. J. Phys., 2002, 23, 11–16 CrossRef CAS.
- E. Canadell, M.-L. Doublet and C. Iung, Orbital Approach to the Electronic Structure of Solids, Oxford University Press, 2012 Search PubMed.
- P. Hansmann, L. Vaugier, H. Jiang and S. Biermann, J. Phys.: Condens. Matter, 2013, 25, 094005 CrossRef PubMed.
- P. Fazekas, Lecture notes on electron correlation and magnetism, World Scientific, Singapore, River Edge, N.J, 1999 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802 CrossRef.
- S. Refaely-Abramson, R. Baer and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144 CrossRef.
- V. Atalla, M. Yoon, F. Caruso, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165122 CrossRef.
- J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussion 09 (Revision A. 02), Wallingford CT, 2009 Search PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mh00023h |
| This journal is © The Royal Society of Chemistry 2015 |
