QM/MM MD simulations of La(III)–phosphopeptide complexes
Christoph B.
Messner
a,
Günther K.
Bonn
a and
Thomas S.
Hofer
*b
aInstitute of Analytical Chemistry and Radiochemistry, Leopold-Franzens University, Innsbruck, Innrain 80-82, 6020 Innsbruck, Austria
bTheoretical Chemistry Division, Institute of General, Inorganic and Theoretical Chemistry, Leopold-Franzens University, Innsbruck, Innrain 80-82, 6020 Innsbruck, Austria. E-mail: t.hofer@uibk.ac.at
First published on 24th October 2014
Abstract
Several bioanalytical enrichment techniques are based on the interactions of phosphopeptides with Ln(III) ions. In order to gain an improved understanding of these complexes and the respective ion–peptide interactions, hybrid quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations of La(III) coordinating to the phosphopeptide VPQLEIVPNSpAEER were conducted. Simulations of di- as well as monoanionic phosphate groups were carried out. The La(III) ion and its first hydration layer, including the sidechain of the phosphoserine residue were treated quantum mechanically at RI-MP2/triple zeta level, whereas the remaining part of the system was treated with classical potentials. The simulation of the dianionic phosphopeptide revealed a 9-fold coordinated La(III) ion, with the phosphopeptide binding bi- as well as monodentate. The mean residence times (τ) of the first shell water molecules were 82 ps and 37 ps for the bi- and monodentate complexes, respectively, which is much higher compared to free La(III) in aqueous solution (τ = 17 ps). The simulation of the monoanionic La(III)–phosphopeptide complex revealed a bidentate coordination throughout the 80 ps sampling period. An intramolecular hydrogen bond between the hydrogen of the phosphate group and the backbone was observed and a τ value of 14 ps was obtained, which is much lower as for the dianionic complex.
1 Introduction
The reversible phosphorylation of phosphoproteins is an important regulatory mechanism for a number of cellular processes and therefore, the identification and characterization of phosphoproteins/phosphopeptides is an important issue.1 Despite the fast development of mass spectrometric methods, the analysis of phosphopeptides remains challenging due to suppression effects and, therefore, selective enrichment steps prior to measurements are generally applied.2 In recent years, several enrichment strategies based on the interactions of La(III) ions with phosphopeptides and phosphoproteins have been developed, showing exceptionally high selectivities.3–9 Especially the co-precipitation of phosphoproteins3,4 and phosphopeptides7 by lanthanoid(III) ions is a promising alternative to conventional approaches that are mainly based on stationary phases. However, structure and dynamics of La(III)–phosphopeptide complexes in aqueous solution are by now poorly understood.Phosphopeptides and phosphoproteins have been studied by Fourier transform infrared spectroscopy (FTIR),10,111H nuclear magnetic resonance12,13 as well as molecular mechanics (MM) molecular dynamics (MD) simulations.14 Sanchez-Ruiz et al.10 reported a pKa of about 6 for the phosphate monoester in O–phosphoserines by carrying out FTIR measurements. Fernández et al.11 made similar observations for α-casein as a change in pH from 6.8 to 2.0 resulted in a dramatic reduction of the dianionic symmetric stretching peak at 976 cm−1.
Hydrated lanthanum(III) was studied by EXAFS measurements15 as well as by a quantum mechanical charge field (QMCF) MD simulation16 and coordination numbers of around 9 were reported by both groups.
MD simulations are a powerful tool to study systems like La(III)–phosphopeptide complexes. However, the theoretical treatment of such highly charged systems requires quantum mechanical (QM) methods to achieve a sufficiently accurate description of the molecular interactions, since polarization and charge transfer effects play a crucial role.17,18 Unfortunately, QM calculations are restricted to relatively small systems and hence combined quantum mechanical/molecular mechanical (QM/MM) techniques became a popular and highly successful approach.19,20 Recently, the importance of QM/MM methods was underlined by the awarding of the Nobel prize in chemistry to Martin Karplus, Michael Levitt and Arieh Warshel.21 These methods are based on a partitioning of the molecular system into two region, where different levels of theory are applied: the chemically most relevant part is treated by computationally demanding quantum mechanical methods, whereas interactions in the surrounding region are treated with empirical potentials. Therefore, these methods enable a modeling of large molecular systems at reasonable cost while still providing high accuracy at the region of interest. The main challenge of this partitioning is the QM/MM boundary, especially if covalent bonds have to be cut. Two frequently applied approaches to this problem are the link-atom approach and the local self consistent field (LSCF) formalism, with each exhibiting its strengths and drawbacks.22,23
In the present study, QM/MM MD simulations of the complex of La(III) with a phosphopeptide were conducted in order to gain an improved understanding of La(III) based bioanalytical enrichment techniques. The sequence of the studied phosphopeptide is VPQLEIVPNSpAEER. This peptide was chosen for this study as it is present in tryptic digests of α-casein, which are frequently used for bioanalytical studies.
2 Methods
2.1 Simulation protocol
The Berendsen algorithm25 was applied with a relaxation time of 0.1 ps in order to keep the temperature at around 298 K. The velocity Verlet/RATTLE algorithm was used to integrate the equations of motions,26 with constraints being applied to all bonds involving hydrogen atoms. The Coulombic cutoff was set to 15 Å and the long-range electrostatic interactions were considered via the reaction field method (ε = 78.36).27 The FF99SB force field28 was applied to all standard aminoacid residues and the potentials for phosphoserine29 as well as for La(III)30,31 were taken from literature. For water, the extended simple point charge (SPC/E) water model32 was used.
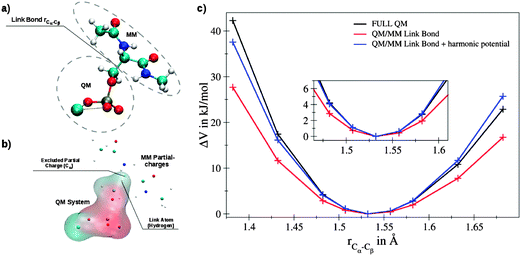
The La(III) ion has been placed in the center of the QM region and all water molecules within a radius of 4.2 Å of La(III) were treated quantum mechanically. To ensure a smooth transition between QM and MM region, a smoothing function33 was applied to all particles located in the so called smoothing region (0.2 Å thick). The phosphoserine residue was further partitioned between Cα and Cβ and only the resulting methylphosphate was treated quantum mechanically. The link-atom approach has been employed to satisfy unsaturated valence and the respective position was determined via:
| rCH = ρ(rCβ − rCα) | (1) |
To evaluate adequate settings for the link bond, QM/MM and full QM calculations of the model system ACE-SER(P)-NME coordinated to a La(III) ion were carried out (Fig. 1a). The corresponding QM setup is shown in Fig. 1b: due to the proximity of the Cα atom, it is excluded when computing the interaction between the QM system and the MM partial charges. Fig. 1c displays the energy obtained upon stretching of the QM/MM link bond for a full QM (black) and the QM/MM setup (red) at MP2 level, using an ideal factor ρ identified as 0.7135. If a properly adjusted MM potential is applied along the link bond (blue), the shape coincided well with the full QM treatment in the region close to the minimum.
The quantum mechanical calculations were conducted with the Turbomole program,34 using the RI-MP235 method. The def-TZVP basis set36 was applied to carbon, hydrogen, oxygen and phosphorus and the def2-TZVP37 basis set with the def2-ECP38,39 was used for La(III). The partial charges of the MM atoms were taken into account via a pertubational term in the core Hamiltonian, however Cα was not considered in order to avoid an unphysical polarization along the linker bond. To generate an appropriate starting structure, an MM simulation was carried out for 25 ns with the previously mentioned force field parameters. Prior to the 80 ps sampling period, the system was equilibrated for 20 ps. The simulation was carried out with the QMCF MD software package.33,40,41
2.2 Analysis
The pair radial distribution function (RDF) gives the probability of finding an atom at a distance r from an other atom compared to the ideal gas distribution.42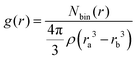 | (2) |
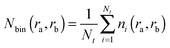 | (3) |
The average coordination numbers (CNav) were evaluated by a numerical integration via the trapezoidal rule43 of all “bins” from 0 to the first minimum of the corresponding RDF (3.7 Å).
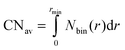 | (4) |
The angular distribution functions (ADF) are histograms based on ligand–ion–ligand angles within a certain radius. La(III) was considered as the center and all oxygens within the first minima of the corresponding RDF (3.7 Å) were considered as ligands.
Spectroscopic data was extracted by analyzing the autocorrelation of the particles' velocity vectors viaeqn (5), where Nt is the number of time origins in the time ti utilized for the autocorrelation of all the velocity components v of a particle j while N is the number of particles under investigation.
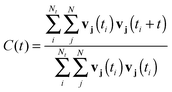 | (5) |
The mean residence time (τ), indicating the average coordination time, was evaluated by the direct method:44
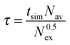 | (6) |
The Root-mean-square deviation was calculated via
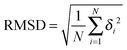 | (7) |
3 Results and discussion
The pKa value of the phosphate monoester in phosphoserines is about 6.10 Therefore, depending on the pH as well as on the La(III) concentration, phosphopeptides might be monoanionic or dianionic in aqueous solutions containing La(III) ions. As enrichment techniques are often applied at low pH, we considered the non-coordinating sites as protonated (carboxylate groups) and conducted simulations with La(III) coordinating towards a protonated as well as a deprotonated phosphoserine residue.3.1 Dianionic La(III)–phosphopeptide
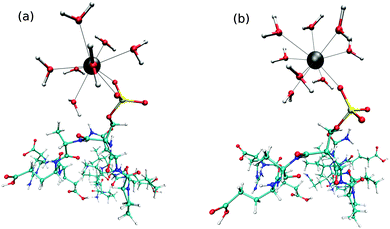
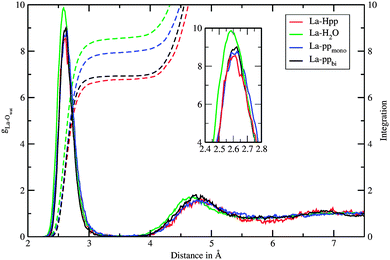
In the first 50 ps of the simulation the phosphate group coordinated bidentately to the La(III) ion (Fig. 2a). Subsequently, a monodentate complex (Fig. 2b) was formed and observed until the end of the sampling period. The mono- and bidentate structures have been evaluated separately and are denoted as La–ppmono and La–ppbi.Average coordination numbers (CNav) of 8.9 and 9.0 were obtained for the bi- and monodentate complexes, respectively (Table 1), which are higher as for free La(III) in aqueous solution ([La(H2O)n]3+) where a CNav of 8.5 was found. Fig. 3 depicts the La–Owat RDFs for both La(III)–phosphopeptide complexes as well as for free La(III) in aqueous solution. Sharp peaks ranging from 2.3 to 3.2 Å indicate the first hydration layers. Compared to free La(III) in aqueous solution, the phosphopeptide complexes exhibit more narrow peaks, which are slightly shifted to larger distances. Furthermore, the peak of La–ppbi is more narrow and slightly shifted to a shorter distance compared to the peak of La–ppmono. The integrations of the first peaks of the RDFs are around 7 and 8 for La–ppbi and La–ppmono, respectively, which correlates with CNav, considering the coordination sites of the phosphopeptide. Well defined peaks are observed at a distance of 3.9 to 5.5 Å, indicating the second hydration layers. Similar to the first hydration shell, slight differences were found between La–ppmono, La–ppbi and [La(H2O)n]3+. The water molecules of the second hydration layers of the La(III)–phosphopeptide complexes have a slightly larger distance from the center compared to the second shell water molecules of [La(H2O)n]3+.
| τ (ps) | CNav | d La–Owat (Å) | |
|---|---|---|---|
| La | 17 | 8.5 | 2.58 |
| La–ppbi | 82 | 8.9 | 2.61 |
| La–ppmono | 37 | 9.0 | 2.62 |
| La–Hpp | 14 | 8.8 | 2.61 |
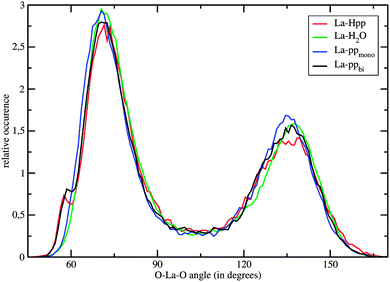
Fig. 4 shows the O–La–O ADFs, with O being all oxygen atoms within a distance of 3.7 Å. The relatively narrow peaks with maxima around 71° and 137° indicate a quite rigid coordination structure, with geometries in-between a tri-capped trigonal prism and a capped square antiprism. The bidentate coordinating complex shows a shoulder at 59°, which results from the Ophosphate–La–Ophosphate angle. Consequently, the 7 water molecules in the first hydration layer of La–ppbi exhibit larger Owat–La–Owat angles than the 8 water molecules in the first shell of La–ppmono, which is indicated in the ADFs by a slight shift of the peak at 71° to larger angles (Fig. 4).
The average partial charge (Mulliken) of the La(III) ion is 2.03, 2.10, and 2.15 for La–ppbi, La–ppmono and [La(H2O)n]3+, respectively. The reduction of the La(III) partial charge is a result of the phosphate group-ion charge transfer. As can be expected this effect is more pronounced in the bidentate coordinating complex.
The τ values for all oxygens within a radius of 3.7 Å are 82 ps, 37 ps and 17 ps for La–ppbi, La–ppmono and [La(H2O)n]3+, respectively. It should be emphasized that these τ values, especially the higher ones, might have some statistical uncertainties. The exceptionally high τ of La–ppbi indicates a more stable 9-fold coordinated structure compared to free La(III) in aqueous solution and this may be attributed to the relatively small Ophosphate–La–Ophosphate angle (Fig. 4), which results in a lower nuclei repulsion of the 7 first shell water molecules. The τ value for La–ppmono is, although not as high as for La–ppbi, higher as for [La(H2O)n]3+. In this complex, a further stabilizing effect might arise from the hydrogen bonds between the first shell water molecules and the oxygens from the phosphate group.
IR spectra were calculated via VACFs and Table 2 lists the most prominent P–O and La–Owat bands. The La–Owat bands of La–ppmono and La–ppbi differ only for about 10 cm−1 and are slightly lower as for [La(H2O)n]3+. The P–O bands, which result from the asymmetric stretching mode, were found at 1090 cm−1 and 1060 cm−1 for La–ppmono and La–ppbi, respectively. The experimentally obtained asymmetric P–O stretching frequency of the dianionic phosphoserine is 1091 cm−1.10
| v La–Owat (cm−1) | v P–O (cm−1) | |
|---|---|---|
| La | 180 | |
| La–ppbi | 150 | 1060 |
| La–ppmono | 160 | 1090 |
| La–Hpp | 160 | 1210 |
During the whole MM MD as well as QM/MM MD simulation, the La(III) ion interacted solely with the phosphate group of the studied phosphopeptide, whereas other aminoacid sidechains (e.g. glutamate) did not interact with the ion. This is in agreement with the experimental observation that Ln(III)-based enrichment techniques demonstrate high selectivities towards phosphorylated residues while non-phosphorylated peptides have been rarely detected using these approaches.7,8 Therefore, interactions of La(III) ions with other monophosphorylated peptides might show similar binding properties. Multiphosphorylated peptides, however, could coordinate with more than one phosphate group toward the ion, possibly triggering a refolding of the peptide.
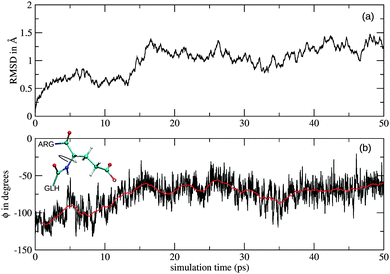
The root-mean-square deviation (RMSD) of the dianionic bidentate complex fluctuates about a constant value of 0.83 Å throughout the sampled 40 ps. The dianionic monodentate complex, however, shows a slight rearrangement after 15 ps, indicated by a small step in the RMSD plot (Fig. 5a). Such changes are in general a consequence of rotations of the backbone. The time series of the CC(GLH12)–N(GLH13)–Cα(GLH13)–CC(GLH13) dihedral angle (ϕ) and the running average is shown in Fig. 5(b) and indicate that the change in the RMSD plot results from a rotation around the N(GLH13)–Cα(GLH13) bond.
3.2 Monoanionic La(III)–phosphopeptide complex
A bidentate coordination was observed throughout the sampling period and an intramolecular hydrogen bond between the hydrogen of the phosphate group and the backbone (Fig. 6) was formed. Fig. 7 displays the time series of the HP–OC distance (left) and the corresponding histogram representation (right), where HP is the proton at the phosphate group and OC the oxygen of the backbone's carbonyl group. The histogram displays the HP–OC distance distribution, with 1.85 Å being the maximum. The first 20 ps of sampling the HP–OC distance fluctuates about this value, indicating the formation of a hydrogen bond. In between 20 ps and 26 ps simulation time, HP–OC distances up to 5 Å were observed. During this period hydrogen bonds to water molecules from the bulk were formed, as shown in the left snapshot in Fig. 7. Similar events, although shorter, were observed in between 30 ps and 35 ps simulation time. Subsequently, the intramolecular hydrogen bond was more or less stable until a simulation time of 60 ps. In between 60 ps and 72 ps sampling, hydrogen bonds to bulk water molecules were observed again (right snapshot in Fig. 7). At a simulation time of 72 ps, the intramolecular hydrogen bond was formed and remained stable until the end of the simulation.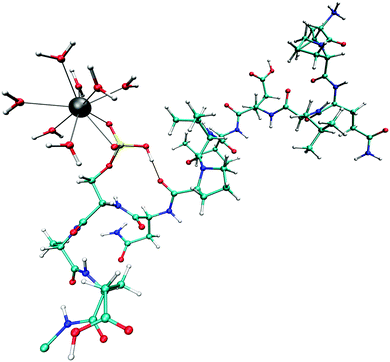 | ||
| Fig. 6 Snapshot taken from the QM/MM MD simulation of the monoanionic La(III)–phosphopeptide complex. Cyan: C; white: H; blue: N; red: O; yellow: P; gray: La(III). | ||
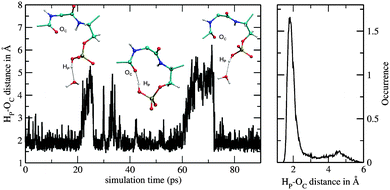 | ||
| Fig. 7 Time series of HP–OC distance (left) and corresponding histogram representation (right) obtained from the QM/MM simulation of the monoanionic La(III)–phosphopeptide. | ||
The La–Owat RDF of the protonated La(III)–phosphopeptide complex (La–Hpp) in Fig. 3 shows a slightly smaller first peak and the CNav is marginally lower (Table 1) compared to La–ppbi. The second peak of the La–Owat RDF is shifted to larger distances, compared to La–ppbi. The reduced number of water molecules at around 6 Å can be attributed to the presence of a valine residue. The partial charge of the La(III) ion is 2.05, which is similar as for the La–ppbi complex.
The τ value for the coordinating oxygen atoms is 14 ps, which is similar to the τ of free La(III) in aqueous solution (Table 1). Although the 9-fold coordinated structure is stabilized by the small Ophosphate–La–Ophosphate angle as discussed above, much more water exchange processes were observed as for the La–ppbi complex. One reason therefore could be the reduced distance to the valine residue. Phosphopeptides with other aminoacid residues at this position (e.g. aspartate) could possibly have the adverse effect by forming hydrogen bonds and hence stabilizing the hydration structure.
An asymmetric stretching frequency of 1210 cm−1 was found which is considerably higher as for the dianionic complex. The experimentally obtained asymmetric stretching frequency of O–phosphoserine is 1194 cm−1.10
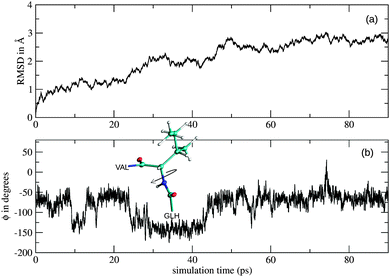
The RMSD plot obtained from the simulation of the monoanionic La(III)–phosphopeptide complex is shown in Fig. 8. Significant changes of the positions of the backbone atoms were observed in between 20 ps and 30 ps as well as in between 40 ps and 50 ps simulation time. These changes could result from rotations around the N(ILE6)–Cα(ILE6) bond, as the CC(GLH5)–N(ILE6)–Cα(ILE6)–CC(ILE6) dihedral angle (ϕ) changes its value almost 100° at 25 ps and 45 ps sampling time (Fig. 8b). Furthermore, the rearrangement in between 20 ps and 30 ps simulation time could be related to the first break of the intramolecular hydrogen bond, which takes place at the same sampling time (Fig. 7).
4 Conclusion
QM/MM simulations of La(III)–phosphopeptide complexes revealed detailed structural as well as dynamical data. The definition of a QM region in combination with the link-atom approach has proven successful in studying the solvation properties of such systems. Due to the constant increase in computational power, the simulations could be conducted at RI-MP2/triple zeta level. The dianionic phosphopeptide was found to coordinate mono- as well as bidentate to the La(III) ion. The exchange rate of the first shell water molecules is much lower as for free La(III) in aqueous solution, indicating an energetically favorable structure which could possibly explain the high selectivity of La(III) based bioanalytical approaches. The observed intramolecular hydrogen in the simulation of the monoanionic La(III)–phosphopeptide complex could result in a stabilization of the acid state and a lowered pKa of phosphoserine.Acknowledgements
This work was supported by the Austrian Ministry of Science BMWF UniInfrastrukturprogramm as part of the Research Focal Point Scientific Computing at the University of Innsbruck.References
- G. Manning, G. D. Plowman, T. Hunter and S. Sudarsanam, Trends Biochem. Sci., 2002, 27, 514–520 CrossRef CAS.
- M. R. Larsen, T. E. Thingholm, O. N. Jensen, P. Roepstorff and T. J. Jørgensen, Mol. Cell. Proteomics, 2005, 4, 873–886 CAS.
- M. Pink, N. Verma, F. Polato, G. K. Bonn, H. A. Baba, A. W. Rettenmeier and S. Schmitz-Spanke, J. Proteomics, 2011, 75, 375–383 CrossRef CAS PubMed.
- Y. Güzel, M. Rainer, M. R. Mirza and G. K. Bonn, Anal. Bioanal. Chem., 2012, 403, 1323–1331 CrossRef PubMed.
- Y. Güzel, M. Rainer, M. R. Mirza, C. B. Messner and G. K. Bonn, Analyst, 2013, 138, 2897–2905 RSC.
- M. Pink, C. Stein, N. Verma, A. W. Rettenmeier and S. Schmitz-Spanke, Electrophoresis, 2013, 34, 501–504 CrossRef CAS PubMed.
- M. R. Mirza, M. Rainer, Y. Güzel, I. M. Choudhary and G. K. Bonn, Anal. Bioanal. Chem., 2012, 404, 853–862 CrossRef CAS PubMed.
- M. R. Mirza, M. Rainer, C. B. Messner, Y. Guezel, D. Schemeth, T. Stasyk, M. I. Choudhary, L. A. Huber, B. M. Rode and G. K. Bonn, Analyst, 2013, 138, 2995–3004 RSC.
- A. Saeed, M. Najam-ul Haq, F. Jabeen and F. Svec, Anal. Chem., 2013, 85, 8979–8986 CrossRef CAS PubMed.
- J. M. Sanchez-Ruiz and M. Martinez-Carrion, Biochemistry, 1988, 27, 3338–3342 CrossRef CAS.
- C. Fernández, S. F. Ausar, R. G. Badini, L. F. Castagna, I. D. Bianco and D. M. Beltramo, Int. Dairy J., 2003, 13, 897–901 CrossRef.
- A. Tholey, A. Lindemann, V. Kinzel and J. Reed, Biophys. J., 1999, 76, 76–87 CrossRef CAS.
- J.-T. Du, Y.-M. Li, W. Wei, G.-S. Wu, Y.-F. Zhao, K. Kanazawa, T. Nemoto and H. Nakanishi, J. Am. Chem. Soc., 2005, 127, 16350–16351 CrossRef CAS PubMed.
- S. E. Wong, K. Bernacki and M. Jacobson, J. Phys. Chem. B, 2005, 109, 5249–5258 CrossRef CAS PubMed.
- I. Persson, P. D'Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Chem. – Eur. J., 2008, 14, 3056–3066 CrossRef CAS PubMed.
- O. Lutz, T. S. Hofer, B. R. Randolf and B. M. Rode, Chem. Phys. Lett., 2012, 536, 50–54 CrossRef CAS PubMed.
- T. S. Hofer, B. R. Randolf and B. M. Rode, Phys. Chem. Chem. Phys., 2005, 7, 1382–1387 RSC.
- T. S. Hofer, A. K. H. Weiss, B. R. Randolf and B. M. Rode, Chem. Phys. Lett., 2011, 512, 139–145 CrossRef CAS PubMed.
- M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- The Nobel Prize in Chemistry 2013 - Press Release http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2013/press.html, accessed July 2014.
- N. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem. A, 2000, 104, 1720–1735 CrossRef CAS.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185–199 CrossRef CAS.
- D. A. Case, T. A. Darden, T. E. Cheatham, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Goetz, I. Kolossvry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, W. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, University of California, San Francisco, 2012.
- H. J. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS PubMed.
- H. C. Andersen, J. Comput. Phys., 1983, 52, 24–34 CrossRef CAS.
- D. J. Adams, E. M. Adams and G. J. Hills, Mol. Phys., 1979, 38, 387–400 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- N. Homeyer, A. H. Horn, H. Lanig and H. Sticht, J. Mol. Model., 2006, 12, 281–289 CrossRef CAS PubMed.
- M. Baaden, M. Burgard, C. Boehme and G. Wipff, Phys. Chem. Chem. Phys., 2001, 3, 1317–1325 RSC.
- F. C. van Veggel and D. N. Reinhoudt, Chem. – Eur. J., 1999, 5, 90–95 CrossRef CAS.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- B. M. Rode, T. S. Hofer, B. R. Randolf, C. F. Schwenk, D. Xenides and V. Vchirawongkwin, Theor. Chem. Acc., 2006, 115, 77–85 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1993, 85, 441–450 CrossRef CAS.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- B. M. Rode and T. S. Hofer, et al. , Pure Appl. Chem., 2006, 78, 525–539 CrossRef CAS.
- T. S. Hofer, A. B. Pribil and B. R. Randolf, et al. , Adv. Inorg. Chem., 2010, 62, 143–175 CrossRef CAS.
- A. R. Leach, Molecular modelling: principles and applications, Pearson Education, 2001 Search PubMed.
- K. E. Atkinson, An introduction to numerical analysis, John Wiley & Sons, 2008 Search PubMed.
- T. S. Hofer, H. T. Tran, C. F. Schwenk and B. M. Rode, J. Comput. Chem., 2004, 25, 211–217 CrossRef CAS PubMed.
- A. J. Lock, S. Woutersen and H. J. Bakker, Vibrational relaxation and energy equilibration in liquid water, in Femtochemistry and Femtobiology, ed. A. Douhal and J. Santamaria, World Scientific, Singapore, 2002, pp. 234–239 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |