Avoiding pitfalls in L1-regularised inference of gene networks†
Andreas
Tjärnberg‡
ab,
Torbjörn E. M.
Nordling‡
*acd,
Matthew
Studham
a,
Sven
Nelander
cd and
Erik L. L.
Sonnhammer
abe
aStockholm Bioinformatics Centre, Science for Life Laboratory, Box 1031, 17121 Solna, Sweden. E-mail: tn@nordron.com
bDepartment of Biochemistry and Biophysics, Stockholm University, Sweden
cDepartment of Immunology, Genetics and Pathology, Uppsala University, Rudbeck laboratory, 75185 Uppsala, Sweden
dScience for Life Laboratory, Uppsala University, Sweden
eSwedish eScience Research Center, Sweden
First published on 22nd October 2014
Abstract
Statistical regularisation methods such as LASSO and related L1 regularised regression methods are commonly used to construct models of gene regulatory networks. Although they can theoretically infer the correct network structure, they have been shown in practice to make errors, i.e. leave out existing links and include non-existing links. We show that L1 regularisation methods typically produce a poor network model when the analysed data are ill-conditioned, i.e. the gene expression data matrix has a high condition number, even if it contains enough information for correct network inference. However, the correct structure of network models can be obtained for informative data, data with such a signal to noise ratio that existing links can be proven to exist, when these methods fail, by using least-squares regression and setting small parameters to zero, or by using robust network inference, a recent method taking the intersection of all non-rejectable models. Since available experimental data sets are generally ill-conditioned, we recommend to check the condition number of the data matrix to avoid this pitfall of L1 regularised inference, and to also consider alternative methods.
1 Introduction
Gene regulatory network (GRN) inference, also known as reverse engineering or network reconstruction, is an essential endeavour in systems biology. Several studies1–3 state that mRNA transcriptional regulatory networks can be inferred based on gene expression data obtained from in vivo experiments in which all genes of interest are systematically perturbed and the resulting expression changes are measured. To be biologically realistic, the network needs to be relatively sparsely connected, in other words, only a fraction of all possible links exist. The LASSO method4 and its derivatives, all of which use L1-regularisation to induce sparsity, achieve this and have become popular for GRN inference. Several other modelling techniques exist such as Bayesian,5,6 information theoretic,7,8 neural networks,9,10 Boolean11,12 and dynamical systems.1,13 Nonetheless, in this study we focus on L1-regularisation methods, in particular LASSO, Elastic Net,14 and Bolasso,15 due to their widespread usage. We show that they fail to infer the correct network even when the data are informative enough for correct inference by other methods. We also test the methods on the in vivo data collected by Lorenz et al.2 for inference of the Snf1 network in S. cerevisiae and relate the results to our simulations on in silico data with known golden standard networks.Theoretically, LASSO has been shown to be able to recover the correct network under certain conditions, such as the Strong Irrepresentable Condition (SIC) and Restricted Isometry Property (RIP).16–18 In a network inference context, these conditions concern the relation among observed vectors of expression changes. However, even results based on SIC only ensure that the LASSO estimator is sign consistent with a probability that goes to one as the number of samples goes to infinity. Some of the inferred links could thus not exist in reality, in particular for the low number of samples seen in biological data sets. In real applications, SIC is of little use because it cannot be calculated without knowing the true network. Even though performance of L1-regularisation methods has been analysed rather extensively, we have not seen any article reporting that they fail for sufficiently informative data, which we show here.
In a number of cases, when reverse engineering algorithms have been applied to biological networks, believed to have a well understood connectivity, networks with a different connectivity have been obtained. For instance, Lorenz et al.2 reported a mere 62% sensitivity and 69% precision with 24% of the predicted regulatory interactions having the opposite sign in the model of the Snf1 network in S. cerevisiae. Moreover, benchmarking studies, such as the Dialogue for Reverse Engineering Assessments and Methods (DREAM), have shown that GRN inference usually results in a large fraction of false positives, i.e. inferred links absent in the true network, and false negatives, i.e. missed links present in the true network.19,20 This has in later years lead researchers to complement expression data with other data types, such as binding data, ChIP-seq, and a priori information.21,22 Note that we here speak about addition of other data types to guide the inference method and not integration of other data types in the model. In the former case the degree of freedom of the model is kept fixed and the data are intended to constrain model parameters, while the degree of freedom in the latter case is increased. Use of these, so called multi-data-type genomic datasets, makes it harder to assess the performance of inference methods compared to expression data alone. It is in particular harder to know to which degree a link is supported by expression data versus a priori information. Even if the complete topology of the network is provided, e.g. from ChIP binding data, the signs (activation/repression) of the links still need to be inferred. Addition of other data does not fix the method per se. We therefore think that awareness of the pitfall of L1-regularisation methods that we report here is more essential than before.
A number of GRN inference benchmark studies23–25 have been published, spanning a wide range of methods and data sets. In general, the conclusion is that although they tend to perform better than random, all inference methods produce models that are far from correct. The dependency on the nature of the data is strong as a method may do well in one benchmark but poorly in another one. Selection of the regularisation coefficient, which determines the sparsity of the estimate, is a major issue because it must be correct for the estimated network model to be correct.26 Vinh et al.27 detail the difficulties of benchmarking, especially on small networks, where sparsity cannot be achieved to any larger degree due to the network's small size. They show that methods for inference of GRNs do not construct any good networks with sufficient confidence and that the parameter settings of the algorithms are crucial to find a good estimate of the structure of the network. However, no method for optimising these crucial parameters is given. Jörnsten et al.28 show that the structural agreement between network models inferred for the same biological system using bootstrapping based on measurements obtained at two different platforms only is good for a narrow range of the regularisation coefficient. This makes it important to assess how the accuracy of different inference methods depends on data and system properties, which we here do for five methods.
Data sets generated in vivo for gold standard networks are rare for benchmark purposes due to a lack of knowledge about the interactions among the genes. An attempt has been made to create such a gold standard for benchmarking by recording an in vivo data set from a synthetically engineered five gene network in yeast, called IRMA.3 Penfold and Wild24 benchmarked time series algorithms in addition to steady-state algorithms and evaluated their performance on IRMA. They found that no methods could retrieve the designed structure of IRMA from the data. The IRMA network was perturbed by single gene over-expression to trigger the response of the network and the change in mRNA abundance was then measured when the system had reached steady-state, as well as a time series sampled either every 10 or 20 minutes for up to 5 hours. For single gene perturbations there is no guarantee that the gene space is sufficiently excited to give informative data, i.e. that a sufficient variation in the response of the genes over the experiments is achieved.29 Another issue with gold standard networks is the definition of a link. The inference method and model formalism have to yield the same type of links as recorded in the gold standard in order for a comparison to be meaningful and fair. The five methods employed here infer so called influences, while gold standard networks typically contain links corresponding to physical binding between molecules.23 Simulated data sets are thus still necessary for benchmarking due to the lack of “real” data sets that are informative enough for accurate GRN inference and differences in the definition of a link. It is thus not possible to exhaustively demonstrate the pitfalls of L1-regularisation methods on real data, despite the multitude of data that exist. However, we have applied the studied inference methods to the in vivo data collected by Lorenz et al.,2 compared the inferred networks to two reference networks that can be seen as gold standards, and related the accuracies to the expected performance in our simulations based on the properties of the data.
In this study, we focus on analysing network and data properties that are important for the accuracy of GRN inference. In particular, the condition number of the network and response matrices, as well as the Signal to Noise Ratio (SNR), are examined. To this end, we generated a set of linear networks with essential properties similar to real biological GRNs. These were then used to generate both gene expression data sets that have properties similar to published in vivo data and data sets that are informative enough for inference of the correct network. This was done to mimic real data sets, while varying the properties and utilising the advantage of knowing the true network. We restrict ourselves to linear models, because it is sufficient to demonstrate the presented pitfall of L1-regularisation methods. Considering that the class of linear models is a subset of the class of nonlinear models, awareness of this pitfall is essential also when inferring a nonlinear model. By identifying easily testable conditions that need to be satisfied for successful GRN inference, we provide guidelines useful for avoiding pitfalls that can cause poor network models.
2 Problem description
In this paper we make the common assumption that the GRN can be described by a linear dynamical systems model1,30,31 | (1) |
| Y = −A−1P + A−1F + E | (2) |
By taking the transpose of the variables and “true” network model, and introducing the notation used for regressors Φ ≜ [ϕ1,…,ϕj,…,ϕN] = YT, regressands Ξ ≜ [ξ1,…,ξi,…,ξN] = −PT, regressor errors ϒ ≜ [υ1,…,υj,…υN] = ET, and regressand errors Π ≜ [ε1,…,εi,…εN] = −FT, we obtain the matrix form of the standard linear data model used in errors-in-variables regression problems
Φ =  + ϒ, Ξ = + ϒ, Ξ =  + Π + Π | (3a) |
ΦǍT = 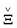 Φ, Ξ ∈ Φ, Ξ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) M×N. M×N. | (3b) |
3 Materials and methods
3.1 Network inference algorithms
Least Absolute Shrinkage and Selection Operator (LASSO) penalises models with small nonzero parameters by introducing a L1 penalty term in the objective function which equals the sum of the absolute values of the parameters4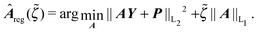 | (4) |
The Elastic net14 is a method based on LASSO which combines the L1 penalty from LASSO and the L2 penalty from ridge regression. The influences of the penalties are then weighted by a parameter α such that,
 | (5) |
Bolasso15 is a bootstrap approach to LASSO inference, where the statistical properties of bootstrapping are combined with the LASSO, see algorithm 1. We use a constant number of bootstraps, nBS = 100, for each data set, as the statistical confidence should increase with nBS. This is well above the minimum number of bootstraps needed,15 , with N being the number of variables. We extend the bootstrap algorithm by requiring that the bootstrapped data set has the same rank as the original data. In practice this means putting a rank requirement on the P matrix so that it has full row rank. This improves the performance, because it ensures that all genes are perturbed in at least one experiment, which is a necessary condition for correct inference.32 Bolasso was not applied to the 10 gene data sets because the data matrix becomes rank deficient if a sample that is left out during the bootstrap procedure contains the only perturbation of a gene. This is often the case in the 10 gene data, and the consequence is that links cannot achieve 100% bootstrap support if they can only be inferred when that unique experiment is sampled. For the same reason, Bolasso was not applied to the data reported by Lorenz et al.2 as it only consists of one set of single gene perturbations, leading to a rank deficient data matrix as soon as one of the experiments is excluded during the bootstrap procedure.
, with N being the number of variables. We extend the bootstrap algorithm by requiring that the bootstrapped data set has the same rank as the original data. In practice this means putting a rank requirement on the P matrix so that it has full row rank. This improves the performance, because it ensures that all genes are perturbed in at least one experiment, which is a necessary condition for correct inference.32 Bolasso was not applied to the 10 gene data sets because the data matrix becomes rank deficient if a sample that is left out during the bootstrap procedure contains the only perturbation of a gene. This is often the case in the 10 gene data, and the consequence is that links cannot achieve 100% bootstrap support if they can only be inferred when that unique experiment is sampled. For the same reason, Bolasso was not applied to the data reported by Lorenz et al.2 as it only consists of one set of single gene perturbations, leading to a rank deficient data matrix as soon as one of the experiments is excluded during the bootstrap procedure.
| Algorithm 1 Plain bootstrap LASSO algorithm. B is the inferred model and A the logical intersection of inferred models. aij is a link from j to i. nBS is the number of bootstraps. | ||
|---|---|---|
| procedure BOOTSTRAP LASSO(data,nBS) | ||
| a ij = 1 ∀ i and j ∈ A | ||
| for 1:nBSdo | ||
| dataBS = DRAW WITH REPLACEMENT(data) | ||
| B = LASSO(dataBS,ζ) | ||
| A = A ∧ LOGICAL(B) | ||
| end for | ||
| A = {aij ∈ A} | ||
| end procedure | ||
| function DRAW WITH REPLACEMENT(data) | ||
| Draw samples with replacement | ||
| s.t. |dataBS| = |data| | ||
| return dataBS | ||
| end function | ||
Least-Squares Cut-Off (LSCO) is a simple inference algorithm based on ordinary least squares (OLS) followed by the removal of all weak links, i.e. small nonzero parameters,
 | (6) |
Robust Network Inference (RNI) is achieved by implicitly checking all network models that cannot be rejected based on the assumed data model and the desired significance level and only including the links that are present in all of these models.32 This gives the intersection of all non-rejectable models. In practice, the network model is obtained by calculating Nordling's confidence score and only including links with a value above one. Nordling's confidence score for the existence of the link aij is defined as
| γ(aij) ≜ σN(Ψ(χ)), | (7a) |
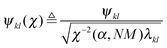 | (7b) |
| and Ψ ≜ [ϕ1,…,ϕj−1,ϕj+1,…,ϕN,ξi], | (7c) |
3.2 Networks
To assess the performance of the inference methods we generated a number of networks by varying model properties that have been considered important in the literature.29,34–36 The sparsity of the networks was set to 0.25 for N = 10 based on reported sparsities. For instance, the data for the ten gene network of the Snf1 signalling pathway in S. cerevisiae2 can be explained well with networks having a sparsity in the range 0.22 to 0.28 and 29 transcriptional regulatory influences have been reported for it in the literature. For N = 45 we generated networks with a sparsity around 0.07. Sparsity is defined as the fraction of links present in the network, denoted L, relative to the total number of possible links, N2, i.e.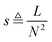 . The interampatteness degree for a linear system is defined as the condition number of the system matrix G = A−1.29 It is thus
. The interampatteness degree for a linear system is defined as the condition number of the system matrix G = A−1.29 It is thus  , where σ1(A) and σN(A) are the largest and smallest singular values of the network matrix A, respectively, for each network. We picked a small value between κ ∈ [0.5,1]·N, and a large value κ ∈ [9,11]·N, with 10 networks for each level. The latter is within the range reported for real networks based on data for a ten gene network of the Snf1 signalling pathway in S. cerevisiae 253, and a nine gene subnetwork of the SOS pathway in E. coli 54.1,2,29 We generated the networks randomly, while making sure the networks have full rank, and weighted the model parameters to ensure stability,37 and that we achieved the desired κ(A).
, where σ1(A) and σN(A) are the largest and smallest singular values of the network matrix A, respectively, for each network. We picked a small value between κ ∈ [0.5,1]·N, and a large value κ ∈ [9,11]·N, with 10 networks for each level. The latter is within the range reported for real networks based on data for a ten gene network of the Snf1 signalling pathway in S. cerevisiae 253, and a nine gene subnetwork of the SOS pathway in E. coli 54.1,2,29 We generated the networks randomly, while making sure the networks have full rank, and weighted the model parameters to ensure stability,37 and that we achieved the desired κ(A).
Tables 1 and 2 gives an overview of the N = 10 and N = 45 network properties respectively. For a complete list of the networks and properties see Tables S3 and S4 (ESI†).
| Network properties | Low κ(A) | High κ(A) |
|---|---|---|
| # Genes, N | 10 | 10 |
| # Networks | 10 | 10 |
| Structure | Random | Random |
| Interampatteness degree, κ(A) | 6.9–10 | 91.6–108 |
| Sparsity | 0.25 | 0.25 |
| Network properties | Low κ(A) | High κ(A) |
|---|---|---|
| # Genes, N | 45 | 45 |
| # Networks | 10 | 10 |
| Structure | Random | Random |
| Interampatteness degree, κ(A) | 25.4–41.3 | 411.5–492.8 |
| Sparsity | ≈0.07 | ≈0.07 |
3.3 Data sets
Data sets were created according to the linear dynamical model in (2). Given the true network Ǎ we calculate an initial P, generated with the given perturbation design. Our noiseless expression data are then![[Y with combining caron]](https://www.rsc.org/images/entities/b_i_char_0059_030c.gif) = −Ǎ−1P. We included 2N samples for N = 10 and 4N samples for N = 45, because published data sets typically contain one to three replicates of N experiments.1–3
= −Ǎ−1P. We included 2N samples for N = 10 and 4N samples for N = 45, because published data sets typically contain one to three replicates of N experiments.1–3
We followed three different perturbation approaches two for N = 10: Naive Random Double Perturbation (NRDP) and Sparse Balanced Excitation Design (SBED), and one for N = 45: triple Single Sets and a Single Double set (SSSD).
NRDP was constructed by perturbing two randomly chosen genes for each sample while making sure that P had full rank and that each gene was perturbed at least once. By perturbing genes more than once we make sure that each sample has some dependency on the remaining data set, a requirement for using the sample in leave one out cross-optimisation of ζ.26 This design yields data sets where the condition number of Y is close to the interampatteness degree of the network. We therefore generate data sets with similar conditions to those reported in the literature, 5, 154, and 215, respectively, in Gardner et al.,1 Alter et al.34 and Lorenz et al.2
The objective of the SBED is to excite all directions of the gene space uniformly, i.e. spread out the response equally in the gene space, and obtain a well conditioned Y matrix.29 We do this approximately by minimising κ(Y) and the number of perturbed genes. To achieve uniform excitation is simpler for a dense perturbation matrix P as the different signal directions in Y can be more easily tuned. However as the possibility to perturb a majority of the genes at once is unrealistic, we keep P as sparse as possible, i.e. we do a trade-off between a sparse perturbation design and uniform excitation in all directions of the gene space.
The SSSD perturbation design is constructed by using triple replicates where a single gene is perturbed for each sample with one extra set of double perturbation where two random genes are perturbed for each sample. This setup simulates a plausible experimental design approach that naively tries to maximise the information in the data set while utilising the fact that there needs to be a dependence between samples to do some form of cross validation.
Tables 3 and 4 shows an overview of data set properties. For a complete list of the data sets and properties see Tables S1, S2 and S5 (ESI†).
| Data set property | ||
|---|---|---|
| Perturbation design | SBED | NRDP |
| Samples, M | 2N | 2N |
| # Data sets | 20 | 20 |
| Condition number, κ(Y) | 1.3–2.0 | 9.5–181.3 |
| Max # perturbations per sample | 2–6 | 2 |
| Min # perturbations per sample | 1–3 | 2 |
| Data set property | ||
|---|---|---|
| Perturbation design | SSSD | SSSD |
| Samples, M | 4N | 4N |
| # Data sets | 10 | 10 |
| Condition number, κ(Y) | 25.7–41.3 | 412.8–504.51 |
| Max # perturbations per sample | 2 | 2 |
| Min # perturbations per sample | 1 | 1 |
We applied noise to each data set with a variance λ selected to give the desired Signal to Noise Ratio (SNR)
 | (8) |
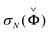 is the Nth singular value of
is the Nth singular value of  , and χ−2(α,NM) is the inverse of the chi-square cumulative distribution function as explained above. We generated 100 different noise realisations to do Monte Carlo simulations, each from a normal distribution with zero mean and variance λ using the randn function in Matlab version R2012a (www.mathworks.com). For each data set, the variance of each realisation was then scaled based on (8) to achieve the desired SNR. For the data sets we used the significance level α = 0.01. By covering the whole range of SNRs from completely uninformative to informative enough, we include the levels seen in real data.
, and χ−2(α,NM) is the inverse of the chi-square cumulative distribution function as explained above. We generated 100 different noise realisations to do Monte Carlo simulations, each from a normal distribution with zero mean and variance λ using the randn function in Matlab version R2012a (www.mathworks.com). For each data set, the variance of each realisation was then scaled based on (8) to achieve the desired SNR. For the data sets we used the significance level α = 0.01. By covering the whole range of SNRs from completely uninformative to informative enough, we include the levels seen in real data.
3.4 Performance evaluation
We assessed the accuracy of the estimated networks using the Matthew Correlation Coefficient (MCC).38 MCC accounts for both true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN), providing one number in the range [−1,1] that captures the structural similarity between two networks containing the same labelled nodes. To use it one needs a golden standard that is taken as the true network that all the estimates are compared to.The Fraction of Provably Existing Links (FPEL) is the fraction of links existing in the true network that can be proven to exist based on the observed data. They are proven to exist by rejecting all alternative network models lacking these links at a desired significance level based on the observed data and true data model, i.e. when the considered set of network models contains the true network and the measurement noise is described by the error model that was used to generate it. FPEL is calculated as the number of links with Nordling's confidence score (7) above one divided by the number of links in the true network.32 It is the sensitivity of RNI. If all existing links can be proven to exist, i.e. FPEL = 1, then the data set is said to be informative enough for network inference. Note that FPEL and MCC are not directly comparable, since only the latter accounts for FP and TN. MCC is relative to the number of possible links N2, while FPEL is relative to the number of links present in the true network L. Nonetheless, MCC = 1 corresponds to FPEL = 1 for RNI. Only measurement data and an error model are needed to calculate the number of provably existing links, implying that it can be used for validation even when no golden standard or true network exists.
3.5 Analysis of the irrepresentable condition
The network model in (3b) can for each row i of the interaction matrix A be expressed as , yielding a sparse estimation problem for each row. By introducing Φ0i and Φ0ci that contain regressors corresponding to the zero and nonzero elements of
, yielding a sparse estimation problem for each row. By introducing Φ0i and Φ0ci that contain regressors corresponding to the zero and nonzero elements of 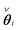 , respectively, and βi containing the nonzero elements of
, respectively, and βi containing the nonzero elements of  , the Common part of the Irrepresentable Conditions (CIC), used by Zhao and Yu16 in theorems ensuring sign consistency of the LASSO estimator, can be expressed as
, the Common part of the Irrepresentable Conditions (CIC), used by Zhao and Yu16 in theorems ensuring sign consistency of the LASSO estimator, can be expressed as | (9) |
If all elements of ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) i are smaller than 1, then the Weak Irrepresentable Condition (WIC) is fulfilled and if all elements are smaller than 1 minus a positive constant η, then the Strong Irrepresentable Condition (SIC) is fulfilled.16 The latter is used to show that LASSO is strongly sign consistent and the former that it is general sign consistent; both imply that the probability that all elements in the LASSO estimate of θi have the correct sign goes to one when the number of samples M goes to infinity. A few additional technical conditions are required in the theorems, but it is logical to expect a high accuracy of the network estimate produced by LASSO when
i are smaller than 1, then the Weak Irrepresentable Condition (WIC) is fulfilled and if all elements are smaller than 1 minus a positive constant η, then the Strong Irrepresentable Condition (SIC) is fulfilled.16 The latter is used to show that LASSO is strongly sign consistent and the former that it is general sign consistent; both imply that the probability that all elements in the LASSO estimate of θi have the correct sign goes to one when the number of samples M goes to infinity. A few additional technical conditions are required in the theorems, but it is logical to expect a high accuracy of the network estimate produced by LASSO when
 | (10) |
If all columns in Φ0i are orthogonal to all columns in Φ0ci, then ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) i = 0 and SIC are fulfilled. Assume for a moment that Φ0i = ϕ1 and Φ0ci = ϕ2, then
i = 0 and SIC are fulfilled. Assume for a moment that Φ0i = ϕ1 and Φ0ci = ϕ2, then ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) i = |ϕT1ϕ2∥ϕ2∥−2|. Now if ϕ1 = αϕ2, i.e. ϕ1 is parallel to ϕ2, then
i = |ϕT1ϕ2∥ϕ2∥−2|. Now if ϕ1 = αϕ2, i.e. ϕ1 is parallel to ϕ2, then ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) i = |α| is greater or equal to one unless α is smaller than one, i.e. unless ϕ1 is shorter than ϕ2. Hence the projection of any regressor corresponding to a zero element that is not orthogonal to the regressors corresponding to a nonzero element onto them must always be shorter than all of them to fulfill SIC. This would always hold if all regressors corresponding to a zero were shorter than all regressors corresponding to a nonzero element. This makes it interesting to calculate the minimum ratio between the shortest regressor corresponding to a nonzero element and the longest corresponding to a zero over all rows
i = |α| is greater or equal to one unless α is smaller than one, i.e. unless ϕ1 is shorter than ϕ2. Hence the projection of any regressor corresponding to a zero element that is not orthogonal to the regressors corresponding to a nonzero element onto them must always be shorter than all of them to fulfill SIC. This would always hold if all regressors corresponding to a zero were shorter than all regressors corresponding to a nonzero element. This makes it interesting to calculate the minimum ratio between the shortest regressor corresponding to a nonzero element and the longest corresponding to a zero over all rows
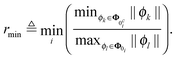 | (11) |
4 Results and discussion
We first present a comparison of the accuracy of the network models yielded by LASSO, Elastic Net, LSCO, and RNI as a function of the SNR for two different groups of data sets from 10 gene networks. One set generated by SBED in which the condition number of the response matrix, Y, is low and another generated by NRDP in which it is high. Similarly, we also compare the accuracy of the network models yielded by LASSO, Elastic Net, Bolasso, LSCO, and RNI for data sets from 45 gene networks. We used the network inference methods LASSO, Elastic Net and Bolasso as representatives of commonly used algorithms. In addition, we used LSCO and the recently proposed method RNI, which, under the assumptions used to generate our data sets, find all links that can be proven to exist. We then use the irrepresentable conditions to analyse why and when LASSO fails based on these two groups of data sets. Finally, using the in vivo data collected by Lorenz et al.,2 we demonstrate how our simulated results can be used to estimate the performance of the methods when they are applied to biological data.4.1 Vulnerability analysis of GRN inference methods
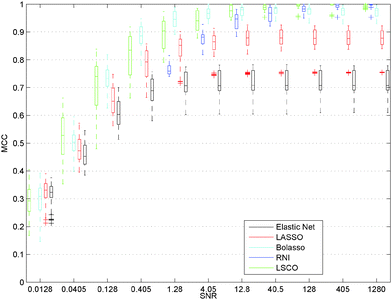
The most striking result on the data set with high response matrix condition number is that all the L1 regularisation methods fail to recover the true network model even when the SNR is so high that the data are informative enough for network inference and all existing links can be proven to exist (Fig. 1 and 3). This unexpected failure of L1 regularisation constitutes an important pitfall in network inference, since many inference methods use L1 penalties and gene expression data sets often have a high condition number.29 Actually the condition numbers of the 20 response matrices with N = 10 are in the range 9 to 181, which is modest compared to the condition number of recorded response matrices used for inference of GRNs, e.g. the ten gene network of the Snf1 signalling pathway in S. cerevisiae (215)2 and the nine gene sub-network of the SOS pathway in E. coli (154).1 Even when the data are so informative that all existing links can be proven to exist using RNI, LASSO in the best case only obtained an MCC of 0.84, while LSCO in all cases for N = 10 recovers the true network. In the N = 45 case Bolasso outperforms LASSO and Elastic Net but fails to recover all links correctly even for the data sets that are informative enough. It is worth noting that Bolasso requires approximately 100 times more computations than LASSO. In LSCO the sum of squared residuals is minimised before any weak link is removed so it will provide good estimates for informative data. We therefore recommend all users of L1 regularisation to check the condition number of the response matrix in order to avoid this pitfall. If it is high, then LSCO and RNI can yield better network estimates.It is important to note that in each case, for each noise realisation, we selected the ζ value that yielded the LASSO estimate that was closest to the true network, i.e. highest MCC for the 100 noise realisations for each noise level, and similarly for Elastic Net, Bolasso, and LSCO. The former was done to avoid the influence of the rule used to select the regularisation coefficient ζ, which typically has a strong influence on the accuracy of the network estimate and is difficult to select correctly.26 Our network estimates are thus in general unrealistically accurate and require knowledge of the true network which is only available for simulated data, yet they are still far from correct. The latter was done to decrease the impact of random effects of the noise realisations in favour of data properties by doing Monte Carlo simulations. For this reason we also used the same 100 noise realisations for all data sets and all SNRs. We varied the network and data properties within ranges deemed reasonable and relevant for network inference based on previous studies. In the literature a single gene is typically perturbed in each experiment, but we here used NRDP, i.e. perturbed two genes in each experiment, selected at random while ensuring that each gene is perturbed and that the perturbations constitute a linearly independent set. We also analysed data sets generated by the typical single gene design and observed the same failure of LASSO (data not shown). A total of 2N (N = 10) or 4N (N = 45) simulated perturbation experiments were used in all data sets, which are comparable to the 3N experiments performed in vivo by Lorenz et al.2 and Gardner et al.,1 respectively.
For the 20 SBED data sets with a response matrix having a low condition number, LASSO, Elastic Net, and LSCO performed equally well and recovered the true network in all cases when the data sets were informative enough for network inference, see Fig. 2. The SBED was in these cases used to balance the excitation of all directions in the space spanned by the 10 genes of the network, so that all singular values of the response matrix were of similar magnitude, while perturbing as few genes as possible in each experiment. These response matrices therefore have condition numbers in the range 1.3 to 2.0, which we have not yet seen for any published gene expression data set. It is worth remembering that we selected the optimal ζ value for each data set and noise realisation for both LASSO, Elastic Net, and LSCO, so the performance is in general unrealistically good. For SNR 0.1, a weak indication of LASSO and Elastic Net outperforming LSCO is present but we cannot say that one method in practice is preferable over the other because the accuracy is sensitive to the selection of the value of the regularisation coefficient ζ.26 The same networks and noise realisations as described above were used.
 | ||
| Fig. 2 GRN inference accuracy versus signal to noise ratio using, Elastic Net, LSCO, and RNI on SBED data sets with N = 10 and low condition number κ(Y). For an SNR of 10, Elastic Net, and LSCO can infer the true network structure for some of the data sets even though all existing links cannot be proven to exist (RNI has a MCC < 1). For an SNR > 10 the median of all methods inference accuracy is approaching 1 and is above 90% for all data sets. For a description of the plot see Fig. 1. | ||
 | ||
| Fig. 3 GRN inference accuracy versus signal to noise ratio for, Elastic Net, Bolasso, LSCO, and RNI on SSSD data sets with N = 45 and high condition number κ(Y). All L1 regularised methods fail even when all existing links can be proven to exist, corresponding to MCC = 1 for RNI. For a description of the plot see Fig. 1. | ||
For the 10 SSSD data sets with a response matrix having a low condition number Bolasso and LSCO performed equally well and recovered the true network in all cases when the data sets were informative enough for network inference, see Fig. 4, while LASSO and Elastic Net performed worse. This is probably due to the condition number of the response matrix being significantly larger than for the 10 gene case in Fig. 2. It is now in the range 26 to 41. We also observe that Elastic Net performs worse than all other methods for the 45 gene case, but have not investigated why. The same networks and noise realisations as described above were used.
 | ||
| Fig. 4 GRN inference accuracy versus signal to noise ratio for, Elastic Net, Bolasso, LSCO, and RNI on SSSD data sets with N = 45 and low condition number κ(Y). For a description of the plot see Fig. 1. | ||
For low SNRs, RNI seems to be partly outperformed by all other methods because of a large number of false negatives, which are a consequence of ensuring that only true positives are included in the network model under the mild assumptions that are fulfilled here, and partly because the optimal regularisation coefficient ζ is selected based on knowledge of the true network. RNI partly performs better than LASSO and Elastic Net from SNR 1 and better than Bolasso from SNR 100 for the data sets with a higher condition number because the SNR is defined based on the weakest singular value and the total excitation hence in general is higher. RNI is mainly included in this study because it gives FPEL and thereby can be seen as a lower bound on the performance that should be required from every other inference method. No other inference method that we are aware of can be used to prove that a link must exist in order to explain the observed data when accounting for the error model of the noise. The ability to prove the existence of links under mild assumptions is in our opinion so valuable in knowledge generation that network models generated by other methods only should be used when the methods outperform RNI.
4.2 When and why does LASSO fail?
The indicators SIC and WIC (Strong and Weak Irrepresentable Conditions) are fulfilled, i.e. μ is below one, only for the data sets with a low condition number and SNR of one or higher, see Fig. 5. This suggests that the response matrix, which is the transpose of the regressor matrix, needs to have a low condition number for accurate GRN estimation using LASSO. In our simulations LASSO typically fails due to introduction of several false positive links, Fig. S2 (ESI†).Another indicator is rmin, the minimum ratio between the shortest regressor corresponding to a nonzero element and the longest corresponding to a zero. All data sets with a low condition number have a considerably higher rmin than all data sets with a high condition number, see Fig. 6. The fact that rmin is below one for all data sets implies that the longest regressor corresponding to a non-existing link exceeds the length of the shortest regressor corresponding to an existing link. For the data sets with a low condition number, the longest regressor corresponding to a non-existing link is expected to be nearly orthogonal to all regressors corresponding to existing links, while in data sets with a high condition number they are not.
 | ||
| Fig. 6 GRN inference accuracy versus minimum ratio between the shortest regressor corresponding to a nonzero element and the longest corresponding to a zero over all rows. A clear separation between data sets where it can infer the true structure (red) and where it cannot (blue) is seen at 0.5 for the ratio rmin. Colours as in Fig. 5. | ||
Evaluation of the irrepresentable conditions and the ratio between the shortest regressor corresponding to a nonzero element and the longest corresponding to a zero requires knowledge of the true network, so they cannot in practice be used to evaluate if LASSO will produce an accurate estimate. The lack of a linear relation between MCC and μ or rmin indicates that neither of the measures captures all aspects that affect the performance of LASSO, so further studies are needed. Until a better testable criterion for failure of LASSO is presented, we recommend all users to check the condition number of the response matrix as discussed above. The condition number has the advantage of being a classical tool in linear algebra that is easy to calculate.
4.3 Analysis of biological data
How well do the tested methods perform on real biological data? Although we cannot control or vary the conditions of real data, we can take a data set and examine how well the methods can use it to infer a reference GRN. Such data e.g. have been collected by Lorenz et al.2 for the Snf1 signalling pathway in S. cerevisiae, and they provide two reference GRNs. They perturbed the ten genes of the Snf1 signalling pathway in S. cerevisiae by inserting a plasmid containing an extra copy of each gene one-by-one and recording the resulting expression change of all ten genes. We calculated the weighted mean variance based on the reported propagated standard error of each data point of the response and perturbation matrix to 0.8 and 0.4, respectively. Because the variance of the response is twice as large as the variance of the perturbations, we calculate the SNR ≈ 0.01 using (8) with α = 0.05. The closest data point based on the number of genes N = 10, the estimated degree of interampatteness 253,32 the condition number κ(Y) = 215, and SNR 0.01 in our simulated data is SNR 0.1 in Fig. 1. Considering that (i) the estimated degree of interampatteness is roughly twice that of the most interampatte simulated 10 gene network (108), (ii) the condition number is larger than the largest condition number of the simulated data sets (181), (iii) the number of perturbations is half, and (iv) the SNR is one order of magnitude lower, the expected MCCs should be well below 0.5. It is worth noting that the expected MCC of RNI is zero, i.e. the data are expected to contain so little information that no link can be proven to exist.To avoid the influence of the selection of the regularisation parameter ζ we varied it over the whole range from a full to an empty inferred network, see supplemental, and report the largest MCC value of each method for each of the networks reported by Lorenz et al.2–S10, S19, and S9. The first golden standard S10 is a collection of links that Lorenz et al.2 found experimental evidence in the literature. To get the second golden standard S19 they complemented these links with links that they found in their validation experiments using ChIP and qPCR. S9 is their final network estimate using NIR39 followed by t-tests keeping only statistically significant interactions. It is not a gold standard but we included it for comparison. Note that a link in these golden standards can mean very different things; anything from a binding observed in a ChIP experiment to an influence on the expression of the other gene. The applied inference methods can only pick up influences that led to expression changes present in the recorded data. It is therefore unlikely that any of these golden standards equal the ``true'' network that would be achieved if more data were collected until Nordling's confidence score for each possible link is either above one or approaches zero. We therefore refrain from making statements about which method that performs best based on comparison to these golden standards. The MCC of LASSO, Elastic Net, LSCO, and RNI is below 0.27 for both golden standards and hence in agreement with our expectation based on our simulations, see Table 5. The MCC between S9 and the two golden standards is below 0.28, i.e. of the same magnitude. The RNI inferred network is empty, indicating that the data contain so little information that no link can be proven to exist.
| S10 | S19 | S9 | |
|---|---|---|---|
| LASSO | 0.18 | 0.22 | 0.36 |
| LSCO | 0.21 | 0.20 | 0.32 |
| Elastic net | 0.18 | 0.27 | 0.40 |
| RNI | 0.00 | 0.00 | 0.00 |
| NIR (S9) | 0.25 | 0.28 | 1.00 |
5 Conclusions
We have shown that all the tested L1 regularisation methods – LASSO, Elastic Net, and Bolasso – typically perform poorly in GRN inference when using data as ill-conditioned as typical experimental data. Testing on the in vivo data collected by Lorenz et al.2 concurs with the expected performance in our simulations based on the properties of the data. As we use the regularisation coefficient that gives the most accurate network for each data set and noise realisation, the here reported performance of LASSO, Elastic Net, Bolasso, and LSCO is in general unrealistically good. We can therefore with certainty say that the L1 regularisation methods fail for ill-conditioned data matrices even when the data are informative enough for network inference, while LSCO in these cases does not. However, this does not necessarily imply that LSCO in practice is always better and preferable over LASSO, Elastic Net, or Bolasso, because the accuracy is sensitive to the selection of the value of the regularisation coefficient.26 Nonetheless, LSCO and RNI can yield better network estimates when the data are ill-conditioned so it is worth applying them. When the data are informative enough for network inference then all existing links can be proven to exist and RNI recovers the correct network structure.32 As can be expected, we observed that LASSO fails when the SIC and WIC criteria are not fulfilled.For both well-conditioned and ill-conditioned data, we found an SNR, as defined in (8), of 10 to be sufficient for LSCO and RNI to achieve maximum accuracies close to one. For data with an SNR below one the accuracy of all methods was in general low. This puts high demands on the quality of experimental data to be useful for GRN inference.
Acknowledgements
This work was supported by the Swedish strategic research programme eSSENCE.References
- T. S. Gardner, D. Bernardo, D. Lorenz and J. J. Collins, Science, 2003, 301, 102–105 CrossRef CAS PubMed.
- D. R. Lorenz, C. R. Cantor and J. J. Collins, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1145–1150 CrossRef CAS PubMed.
- I. Cantone, L. Marucci, F. Iorio, M. A. Ricci, V. Belcastro, M. Bansal, S. Santini, M. Bernardo, D. Bernardo, M. P. Cosma, M. di Bernardo and D. di Bernardo, Cell, 2009, 137, 172–181 CrossRef CAS PubMed.
- R. Tibshirani, J. Roy. Stat. Soc. B, 1996, 58, 267–288 Search PubMed.
- D. Husmeier and A. V. Werhli, Comput. Syst. Bioinf., CSB2007 Conf. Proc., 6th, 2007, 6, 85–95 Search PubMed.
- J. Yu, V. A. Smith, P. P. Wang, A. J. Hartemink and E. D. Jarvis, Bioinformatics, 2004, 20, 3594–3603 CrossRef CAS PubMed.
- J. J. Faith, B. Hayete, J. T. Thaden, I. Mogno, J. Wierzbowski, G. Cottarel, S. Kasif, J. J. Collins and T. S. Gardner, PLoS biol., 2007, 5, e8 Search PubMed.
- X. Zhang, K. Liu, Z.-P. Liu, B. Duval, J.-M. Richer, X.-M. Zhao, J.-K. Hao and L. Chen, Bioinformatics, 2012, 1–8 Search PubMed.
- M. Grimaldi, G. Jurman and R. Visintainer, http://snap.stanford.edu, 2010, 1–8.
- Reconstruction and validation of gene regulatory networks with neural networks, Stuttgart, 2007, pp. 319–24 Search PubMed.
- L. Wang, X. Wang, M. S. Samoilov and A. P. Arkin, Bioinformatics, 2012 Search PubMed , bts634.
- M. A. Beer and S. Tavazoie, Cell, 2004, 117, 185–198 CrossRef CAS.
- S. Nelander, W. Wang, B. Nilsson, Q.-B. She, C. Pratilas, N. Rosen, P. Gennemark and C. Sander, Mol. Syst. Biol., 2008, 4, 216 CrossRef PubMed.
- H. Zou and T. Hastie, J. Roy. Stat. Soc. B: Stat. Meth., 2005, 67, 301–320 CrossRef PubMed.
- F. R. Bach, Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, 2008, pp. 33–40 Search PubMed.
- P. Zhao and B. Yu, J. Mach. Learn. Res., 2006, 7, 2541–2563 Search PubMed.
- E. Candes and M. Wakin, IEEE Signal Processing Magazine, 2008, 25, 21–30 CrossRef.
- E. J. Candès and Y. Plan, Ann. Stat., 2009, 37, 2145–2177 CrossRef.
- D. Marbach, J. C. Costello, R. Küffner, N. M. Vega, R. J. Prill, D. M. Camacho, K. R. Allison, M. Kellis, J. J. Collins and G. Stolovitzky, Nat. Methods, 2012, 9, 796–804 CrossRef CAS PubMed.
- G. Stolovitzky, P. Kahlem and A. Califano, Ann. N. Y. Acad. Sci., 2009, 1158, ix–xii, DOI:10.1111/j.1749-6632.2009.04470.x.
- A. Greenfield, C. Hafemeister and R. Bonneau, Bioinformatics, 2013, 29, 1060–1067 CrossRef CAS PubMed.
- M. E. Studham, A. Tjärnberg, T. E. Nordling, S. Nelander and E. L. L. Sonnhammer, Bioinformatics, 2014, 30, i130–i138 CrossRef CAS PubMed.
- M. Bansal, V. Belcastro, A. Ambesi-Impiombato and D. Di Bernardo, Mol. Syst. Biol., 2007, 3, 78 CrossRef.
- C. A. Penfold and D. L. Wild, Interface Focus, 2011, 1, 857–870 CrossRef PubMed.
- V. Narendra, N. Lytkin, C. Aliferis and A. Statnikov, Genomics, 2011, 97, 7–18 CrossRef CAS PubMed.
- A. Tjärnberg, T. E. Nordling, M. Studham and E. L. Sonnhammer, J. Comput. Biol., 2013, 20, 398–408 CrossRef PubMed.
- N. X. Vinh, M. Chetty, R. Coppel and P. P. Wangikar, Biochim. Biophys. Acta, 2012, 1824, 1434–1441 CrossRef CAS PubMed.
- R. Jörnsten, T. Abenius, T. Kling, L. Schmidt, E. Johansson, T. E. M. Nordling, B. Nordlander, C. Sander, P. Gennemark, K. Funa, B. Nilsson, L. Lindahl and S. Nelander, Mol. Syst. Biol., 2011, 7, 486 CrossRef PubMed.
- T. E. M. Nordling and E. W. Jacobsen, IET Syst. Biol., 2009, 3, 388–403 CrossRef CAS PubMed.
- Y. Yuan, G.-B. Stan, S. Warnick and J. Goncalves, Automatica, 2011, 47, 1230–1235 CrossRef PubMed.
- M. K. Yeung, J. Tegnér and J. J. Collins, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6163–6168 CrossRef CAS PubMed.
- T. E. M. Nordling, PhD thesis, KTH School of Electrical Engineering, Automatic Control Lab, 2013.
- V. Chew, J. Am. Stat. Assoc., 1966, 61, 605–617 CrossRef.
- O. Alter, P. O. Brown and D. Botstein, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 10101–10106 CrossRef CAS.
- J. Tegnér and J. Björkegren, Trends Genet., 2007, 23, 34–41 CrossRef PubMed.
- Z. Wu and Z. Wu, Methods Mol. Biol. (Clifton, N.J.), 2010, 620, 267–284 CAS.
- M. M. Zavlanos, A. A. Julius, S. P. Boyd and G. J. Pappas, Automatica, 2011, 47, 1113–1122 CrossRef PubMed.
- P. Baldi, S. Brunak, Y. Chauvin, C. A. F. Andersen and H. Nielsen, Bioinformatics, 2000, 16, 412–424 CrossRef CAS PubMed.
- D. Di Bernardo, T. S. Gardner and J. J. Collins, Pac. Symp. Biocomput., 2004, 497, 486–497 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4mb00419a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2015 |


