Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient Bayesian estimates for discrimination among topologically different systems biology models†
David R.
Hagen
 ab and
Bruce
Tidor
*abc
ab and
Bruce
Tidor
*abc
aDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: tidor@mit.edu
bComputer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA
cDepartment of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA
First published on 21st November 2014
Abstract
A major effort in systems biology is the development of mathematical models that describe complex biological systems at multiple scales and levels of abstraction. Determining the topology—the set of interactions—of a biological system from observations of the system's behavior is an important and difficult problem. Here we present and demonstrate new methodology for efficiently computing the probability distribution over a set of topologies based on consistency with existing measurements. Key features of the new approach include derivation in a Bayesian framework, incorporation of prior probability distributions of topologies and parameters, and use of an analytically integrable linearization based on the Fisher information matrix that is responsible for large gains in efficiency. The new method was demonstrated on a collection of four biological topologies representing a kinase and phosphatase that operate in opposition to each other with either processive or distributive kinetics, giving 8–12 parameters for each topology. The linearization produced an approximate result very rapidly (CPU minutes) that was highly accurate on its own, as compared to a Monte Carlo method guaranteed to converge to the correct answer but at greater cost (CPU weeks). The Monte Carlo method developed and applied here used the linearization method as a starting point and importance sampling to approach the Bayesian answer in acceptable time. Other inexpensive methods to estimate probabilities produced poor approximations for this system, with likelihood estimation showing its well-known bias toward topologies with more parameters and the Akaike and Schwarz Information Criteria showing a strong bias toward topologies with fewer parameters. These results suggest that this linear approximation may be an effective compromise, providing an answer whose accuracy is near the true Bayesian answer, but at a cost near the common heuristics.
Introduction
In systems biology, mechanistic models of biochemical networks can be seen as a combination of two main components, a topology that defines the set of elementary reactions that occur and a parameter set that defines the rate constants of those interactions and perhaps initial concentrations. By mapping components of the model to components of the system, one can computationally ask what role individual parts of the system play with respect to a particular behavior—what behavior would result if a particular part of the system were altered or what part of the system would have to be altered to effect a desired behavior.Determining the topology of a biological network from data is a difficult and widely studied problem.1–4 The space of possible biological topologies is a discrete one. For a finite number of chemical species, there is a finite, though exponentially large, number of possible ways to connect those species in a network of reactions. In this work, different mathematical formulations of the same network will be considered different topologies. For example, one may wish to test if the data supports using Michaelis–Menten kinetics or mass action kinetics to describe the enzymatic reactions. The two different sets of differential equations would be considered different topologies. There is currently a tradeoff between greater freedom in the mathematical formulation of the topologies and an ability to consider a larger space of topologies, since only some structures have algorithms that can define good topologies without enumerating all possibilities. One can consider three main classes of topology determination methods along this spectrum.
At the most abstract level are the statistical clustering algorithms.5–10 In hierarchical clustering,11 well-known for its use in analyzing microarrays, each state is organized as a leaf on a tree where the distance along the branches indicates the amount of dissimilarity in the behavior of the states either in response to a set of perturbations or over time in response to a single perturbation. If a previously unknown state is clustered closely with several known states, this suggests that the unknown state may be involved in the same role as the known states. However, a specific function or mechanism is not elucidated for any state. Another popular method is principal component analysis, which finds the relationships between the states that explain the most variance under the conditions studied.12 The resulting relationships may reveal the states that are most closely associated with the process that is perturbed between the conditions as well as group the conditions with similar responses. Like hierarchical clustering, such groupings only suggest a coarse organization of the topology, leaving out individual interactions. Methods at this level are widely used because they provide testable hypotheses from very data large sets, even if the studied system is poorly understood.
At the next level are algorithms that reverse engineer causal networks. These algorithms use data to generate de novo interaction networks between states of the system.13–17 These methods exploit a useful mathematical relation between a specific formulation of the model and a specific type of data. An algorithm by Sachs et al. generates an acyclic Bayesian network using single-cell measurements.18 This method exploits the fact that the short-term stochastic fluctuations in one state would be most strongly correlated with the short-term fluctuations of the nearest states. Thus, a causal graph can be built, not by finding the strongest correlations in the states, but by finding the strongest correlations in the stochastic fluctuations of the states about their mean value. Another algorithm by Yeung et al. generates a system of linear ODEs using concentrations of states near a gently perturbed steady state.19 The method exploits the fact that a linear approximation is good near a steady state, allowing a sparse SVD to be used to solve for the topology. By requiring little a priori information, methods at this level bridge the gap between the exponentially large number of possible topologies and a smaller number of topologies supported by the data.
At the most specific level are algorithms that compare the evidence for an enumerated set of topologies. Because one cannot actually enumerate all possible networks for even a small number of states, the set must be shrunk either by assembling topologies based on prior knowledge or by collecting the most favorable topologies generated by a higher-level method like one mentioned in the previous paragraph. These algorithms make use of the likelihood that a topology generated the data to compute the probability that the topology is correct. Several of these methods are used in this work and are described below. Because these methods only require the likelihood of the data, they can be used on a broad range of mathematical modeling techniques such as dynamic nonlinear ODE modeling, which is used in this work.
We phrase the problem of topology probability in a Bayesian framework. Each topology is defined by a pair of functions, a likelihood and a parameter prior. The topologies are indexed by m:
| T(m) = (py|θ,m(y|θ,m),pθ|m(θ|m)) | (1) |
Bayes theorem provides the basic identity for computing the posterior topology probability:
 | (2) |
The marginal likelihood is the probability that a set of data would be observed under a particular topology. Because topologies alone do not generate data (parameterized topologies do) the average probability over all parameters weighted by the prior on the parameters is computed by an integral over parameter space:
 | (3) |
It is difficult and computationally expensive to evaluate the Bayesian result because of the multidimensional integral required to compute the marginal likelihood in eqn (3). This integral does not have an analytical solution for many interesting problems, including mass-action models, and the possibly large number of dimensions of the integral precludes the use of standard quadrature methods such as the trapezoidal rule for numerical integration.
A number of methods have been developed to solve this integral for biological problems.20 All are Monte Carlo methods that compare a known distribution to the unknown posterior distribution and currently require prohibitive computational resources even for simple topologies. To be a known distribution means that its normalization factor, the integral over all space, is known. The simplest methods compare the prior distribution to the posterior distribution while either sampling from the prior (Prior Arithmetic Mean Estimator21) or from the posterior (Posterior Harmonic Mean Estimator22). Unfortunately, these methods are inefficient20,23,24 and cannot be used effectively for any biological system because the difference between the prior and posterior is always large for a topology with more than a few parameters and a few data points, and the size of this difference determines the uncertainty in the estimators.23 Bridge sampling improves on these methods by having one distribution “in between” the prior and posterior to which the prior and posterior are compared, rather than to each other, so that the differences between the compared distributions (and, thus, the variances) are smaller resulting in faster convergence.25 Other methods, such as Thermodynamic Integration,24,26,27 Path Sampling,28 Annealed Importance Sampling,29 and more,30,31 use even more distributions between the prior and the posterior, so that each comparison is between two quite similar distributions resulting in a variance that is low enough to converge for simple biological topologies.32 We tried several of these methods but were unable to find one that would converge in a reasonable time for the system we investigated.
Because of this, we developed our own Monte Carlo method for use here. Our method is similar to the one used by Neal.29 Like almost all methods of this type, ours integrates the marginal likelihood by stepping through a sequence of distributions between the unknown marginal likelihood and a known distribution. Our method uses the linear approximation as the known starting distribution, and the step size from one distribution to the next is generated dynamically to minimize the variance in the answer. A detailed description of our linearized approximation and full Monte Carlo method is provided in the Methods section. The full method was used as the gold standard to which our linearization and other methods were compared.
Because of the computational costs of Monte Carlo methods, approximations to the topology probability are often used instead. The simplest method is to fit each topology to the data and compare the likelihoods of obtaining the data from each topology parameterized by the best-fit parameters.33,34 According to this method, a topology that has a higher likelihood has more evidence in its favor. The method is problematic for one main reason: because topologies have different numbers of parameters, and topologies with more parameters can typically fit data better whether or not they are true, this leads to a bias in favor of more complex topologies and an inability to rule out complex topologies if a simpler topology is true.
To compensate for the shortcomings of a simple comparison of likelihoods, several methods have been developed to appropriately penalize topologies with more parameters. The two most popular are the Akaike Information Criterion (AIC)35 and the Schwarz (or Bayes) Information Criterion (SIC),36 each justified by a different derivation. These heuristics are no more expensive to compute than the likelihood. One assumption of both heuristics is that sufficient data has been collected to make the parameter uncertainty small.37 This is not the case for typical biological models fit to typical data, as our work and that of others has found.38–42 As a result, the heuristics can be quite inaccurate,43,44 which is also the case in the current work.
Unsatisfied with the accuracy of the existing heuristics and computational cost of the Monte Carlo methods, we created an approximation to the topology probability problem that provides an accurate answer but at a lower computational cost. We noticed that, if the model has a linear relationship between the parameters and outputs and the measurements have Gaussian noise, the topology probability has an analytical solution. We wondered if there was a way to linearize the nonlinear model such that it provided an effective approximation to the nonlinear answer. In this work, we derive a method to compute the topology probability for a model linearized at the maximum a posteriori parameters (the best-fit parameters considering the data and prior).
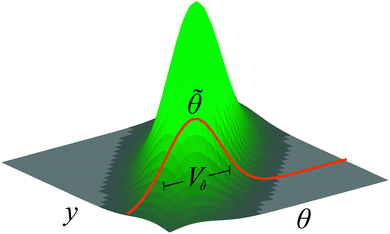
A detailed derivation is provided in the Methods section of this work, but the key insight in developing this method, visualized in Fig. 1, is that the marginal likelihood (eqn 3) of a linear Gaussian model can be written as:
py|m(y|m) = py|θ,m(y|![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m),m)·pθ|m( (y,m),m)·pθ|m(![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m)|m)·∥2·π·V (y,m)|m)·∥2·π·V![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m)∥½ (y,m)∥½ | (4) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m) is the maximum a posteriori parameter set, and V
(y,m) is the maximum a posteriori parameter set, and V![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m) is the posterior variance of the parameters. While the maximum a posteriori parameter set and posterior variance terms have analytic expressions for a linear Gaussian model, each can be computed numerically using nonlinear fitting and numeric integration; thus, using this equation to compute the marginal likelihood provides a linear approximation of the topology probability. This approach is similar to a Laplace approximation but exchanges the Hessian (second-order sensitivities of the negative log posterior) for the Fisher information matrix as the approximation to the inverse of the variance.
(y,m) is the posterior variance of the parameters. While the maximum a posteriori parameter set and posterior variance terms have analytic expressions for a linear Gaussian model, each can be computed numerically using nonlinear fitting and numeric integration; thus, using this equation to compute the marginal likelihood provides a linear approximation of the topology probability. This approach is similar to a Laplace approximation but exchanges the Hessian (second-order sensitivities of the negative log posterior) for the Fisher information matrix as the approximation to the inverse of the variance.
We demonstrated this method on a set of four candidate topologies of MAPK signaling by Ferrell et al.45 We generated random data sets by selecting a random topology from the set of four according to a prior, a random parameter set according to a prior, and a random data set by simulating the model and adding noise. We then asked the various methods (Monte Carlo, linearization, likelihood comparison, AIC, and SIC), to determine which topology had generated the data set and compared the accuracy and speed of the methods. The Monte Carlo method gave the most accurate answer, but took significantly more time, while the heuristics took only the time needed to fit the data, but performed only slightly better than random. The linearization method performed almost as well as Monte Carlo but took no longer than the heuristics. These results suggest that this method is an effective tool for topology discrimination for systems biology.
Methods
Linearization
Important to the linearization method is not just having an analytical solution to the linear model, but writing that solution with terms that can be calculated for the nonlinear model. In this section, we outline the derivation of the analytical solution to the marginal likelihood (eqn (3)) for a model that has a linear relationship between the parameters and the outputs, which are measured with Gaussian noise superimposed. The likelihood function of a topology with this form is defined by:| py|θ,m(y|θ,m) = N(y,ȳ(θ,m),Vy) | (5) |
| ȳ(θ,m) = A(m)·θ + b(m) | (6) |
| py|θ,m(y|θ,m) = N(y,A(m)·θ + b(m),Vy) | (7) |
We also assume that the prior on the parameters is a Gaussian as well:
pθ|m(θ|m) = N(θ,![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (m), Vθ(m)) (m), Vθ(m)) | (8) |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (m) is the mean of the prior on the parameters for topology m (a vector of length nθ(m)) and Vθ(m) is the variance (an nθ(m) by nθ(m) symmetric positive definite matrix).
(m) is the mean of the prior on the parameters for topology m (a vector of length nθ(m)) and Vθ(m) is the variance (an nθ(m) by nθ(m) symmetric positive definite matrix).
Substituting the Gaussian definitions for the likelihood and prior into eqn (3), we get:
 | (9) |
This integral, the marginal likelihood of a linear Gaussian model, has a well-known analytical solution:
py|m(y|m) = N(y,A(m)·![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (m) + b(m), Vy + A(m)·Vθ(m)·A(m)T) (m) + b(m), Vy + A(m)·Vθ(m)·A(m)T) | (10) |
Nonlinear models are not defined using the A(m) and b(m) matrices, so this form is not directly applicable as a linear approximation of nonlinear models. It is known46 and is rederived with matrix transformations in Appendix 1 (ESI†) that this can be rearranged into a convenient form that is the product of the likelihood and prior evaluated at the maximum a posteriori parameter set and a term involving the determinant of the posterior variance:
py|m(y|m) = py|θ,m(y|![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m),m)·pθ|m( (y,m),m)·pθ|m(![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m)|m)·∥2·π·V (y,m)|m)·∥2·π·V![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m)∥½ (y,m)∥½ | (11) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m) is the maximum a posteriori parameter set, the best-fit parameters of topology m for data y, and V
(y,m) is the maximum a posteriori parameter set, the best-fit parameters of topology m for data y, and V![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m) is the posterior variance, which is equal to the inverse of the Fisher information matrix. While the maximum a posteriori parameter values and posterior variance have closed-form solutions for linear Gaussian models (eqn (A5) and (A31) in Appendix 1, ESI†), such an analytic expression does not exist for the topologies we investigated, nor for mass action models in general and many other biological models of interest. Therefore, the best-fit parameters were found using a nonlinear fitting algorithm. The posterior covariance was computed by evaluating the Fisher information matrix at the best-fit parameter set:
(y,m) is the posterior variance, which is equal to the inverse of the Fisher information matrix. While the maximum a posteriori parameter values and posterior variance have closed-form solutions for linear Gaussian models (eqn (A5) and (A31) in Appendix 1, ESI†), such an analytic expression does not exist for the topologies we investigated, nor for mass action models in general and many other biological models of interest. Therefore, the best-fit parameters were found using a nonlinear fitting algorithm. The posterior covariance was computed by evaluating the Fisher information matrix at the best-fit parameter set: | (12) |
 is the ny by nθ(m) sensitivity matrix, calculated by integrating the forward sensitivities with a numerical ODE solver for each topology m parameterized with its best fit parameters
is the ny by nθ(m) sensitivity matrix, calculated by integrating the forward sensitivities with a numerical ODE solver for each topology m parameterized with its best fit parameters ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) (y,m).
(y,m).
The representation of the marginal likelihood in eqn (11) is the central formula to our method. While it is an exact representation for linear models, it is composed of terms that are also well defined for nonlinear models. Since all terms are calculated at the maximum a posteriori parameter set, this formula can be interpreted as a linearization at that point. As we show in Results, this turns out to be a powerfully effective approximation for ODE models of biological systems.
Topologies
As our test case, we used four mass-action ODE topologies of MAPK activation.45 A set of reaction diagrams illustrating these topologies is provided in Fig. 2. The topologies model the double phosphorylation of Erk by Mek. Each topology has a pair of phosphorylation reactions in which the kinase either binds, phosphorylates once, and falls off before rebinding and phosphorylating a second time (distributive mechanism) or, after initial binding, the kinase phosphorylates once and remains bound until a second phosphorylation occurs (processive mechanism). Each topology also has a pair of phosphatase reactions that follow either the distributive or processive mechanisms like the kinase, falling off or remaining bound between reactions. The four possible combinations of these two mechanisms for these two enzymes constitute the four topologies used in this work. As an example of the mathematical form of these topologies, the differential equation for unphosphorylated Erk, which is the same for all topologies, is shown here: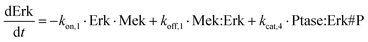 | (13) |
The four model topologies have 12, 10, 10, and 8 parameters in the respective order they will be listed throughout this work and shown in Fig. 2A–D. Each distributive mechanism has two additional parameters for the on and off rates of enzyme rebinding that don't exist for the corresponding distributive topology. Each topology has 8 species, although in topology 4 (processive/processive) the free singly phosphorylated state is not populated. Each topology has 1 input, the amount of kinase, which has a constant value of 1 μM. The initial amount of substrate is 2 μM, the initial amount of phosphatase is 1 μM, and all other initial amounts are 0 μM. These values are comparable to experimental procedures of Ferrell et al.45
There are three outputs, the amounts of unphosphorylated substrate, singly phosphorylated substrate, and doubly phosphosphorylated substrate. The outputs include the amounts of that species that are free or are bound in a complex with the kinase or phosphatase.
Scenario
We set up a computational scenario to generate many data sets from the topologies so that we could interrogate several methods of topology discrimination to determine how well each performed. To generate each data set, a topology was chosen randomly from a uniform distribution (all four topologies were equally likely to be chosen) and the topology was parameterized with random parameters chosen from a multivariate log-normal distribution with a geometric mean of 0.1 and an independent geometric variance such that the 95% confidence intervals stretched 100-fold above and below the geometric mean. This meant that each parameter was essentially chosen over a range of four orders of magnitude.Each randomly drawn model was simulated for 100 minutes and the three outputs were measured at 12.5, 25.0, 37.5, 50.0, 62.5, 75.0, 87.5, and 100.0 min. Each measurement had Gaussian error added to it with a standard deviation equal to 10% plus 0.01 μM. The resulting noisy measurements were floored at 0 (negative values were moved to zero). By measuring the sum of phosphorylation sites across the complexes in which they appear and by only measuring at 8 time points, we intended to represent the modern measurement capabilities of mass spectrometry.47
This scenario was repeated 1000 times to generate that many random models with that many random data sets.
Monte Carlo
The various Monte Carlo methods used to solve this problem are all similar in that they compare the unknown likelihood function to a known likelihood function by sampling from one and comparing the sample in some way to the other.21,22,24,28,29 To be a known likelihood function means that its normalization factor, the integral over all space, is known. The method we use in this work has some conceptual similarity to the Annealed Importance Sampling method,29 but is procedurally very different.To use importance sampling to determine the normalization constant z1 of a distribution determined by likelihood function l1, we sample from a distribution determined by likelihood l0 with known normalization constant z0 and use the following formula to estimate the ratio of the normalization constants:
 | (14) |
 | (15) |
The convergence of this estimator is dependent on the amount of overlap between the known and unknown distributions. If the distributions are similar, the estimator will converge quickly. If the distributions are very different, the estimator will converge slowly. To ensure that the distributions are similar enough, we used a sequence of distributions between the known and unknown distribution defined by the formula:
| l(θ,β) = l0(θ)1−β·l1(θ)β | (16) |
which, by tuning β, gradually transforms the known distribution at β = 0 into the unknown distribution at β = 1.
For the known distribution, we used a linear Gaussian approximation of the posterior by using a nonlinear fitting algorithm to find the maximum a posteriori parameter set (the best-fit parameters) and the Fisher information matrix evaluated at the best-fit parameters. The best-fit parameters became the mean and the inverse of the Fisher information matrix plus the inverse of the prior variance became the variance of a log-normal distribution in parameter space that served as the known, starting distribution of the Monte Carlo procedure.
The final piece of the transformation process is the schedule on β to transform the known distribution into a sequence of unknown distributions culminating in the final unknown distribution. Again, there are many ways to select the points between 0 and 1. The most basic method, a uniform spacing did not allow the Monte Carlo method to converge because the distribution changed far more near the ends than near the middle (data not shown). For example, a change from 0% to 1% or 99% to 100% unknown distribution was a far greater change than going from 49% to 50%. As a result, the importance sampling estimates near the ends had very large uncertainties, but making the steps fine enough to reduce the uncertainty resulted in many wasteful estimates being made of the low-uncertainty middle region. To ensure that each step had a reasonably low variance, we started from β = 0 and determined the next value of β by generating a small sample from the distribution defined by the current value of β and finding, via Matlab's numerical root finder fzero, the value of the next β that would result in a desired sample standard deviation. We chose 0.2, or 20%, as the desired sample standard deviation of each step.
The importance sampling at each span provides an estimate to the change in the integral across that span and an uncertainty in that estimate. The estimates are combined by a simple product:
 | (17) |
The sampling of the posterior was done using the Metropolis–Hastings algorithm.48,49 At each bridge point, the sampling was started at the maximum a posteriori parameter set. The proposal distribution of the algorithm was a log-normal distribution with a geometric mean of the current point and a geometric variance equal to the inverse of the Fisher information matrix plus the inverse of the prior variance computed at the starting point of the sampling multiplied by 5.66 divided by the number of dimensions.50 The log-normal distribution was truncated below 1 × 10−10 and above 1 × 108 to reduce the chance of drawing an extreme parameter set that could destabilize the integrator. The sampling was thinned by saving only every fifth point, and the sampling was restarted every 100 samples after thinning using an updated proposal variance. The autocorrelation in each parameter was computed with Matlab's autocorr function. The sampling was thinned further using the smallest step size such that the estimated autocorrelation in every parameter was less than 0.05. To ensure that the estimate of the autocorrelation was itself accurate, the autocorrelation step size was not trusted until the total length of the sample used to compute the autocorrelation was 20 times longer than the step size.
Akaike Information Criterion
The Akaike Information Criterion (AIC)35 is a popular heuristic for topology discrimination:AIC(m,y) = 2·nθ(m) − 2·log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) py|θ,m(y| py|θ,m(y|![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) (y,m),m) (y,m),m) | (18) |
 | (19) |
The ranking of topologies under this metric is the same, but makes the values comparable to the Monte Carlo and linear methods.
Schwarz Information Criterion
The Schwarz (or Bayes) Information Criterion (SIC)36 is another popular heuristic for topology discrimination:SIC(m,y) = nθ(m)·log(ny) − 2·log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) py|θ,m(y| py|θ,m(y|![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) (y,m),m) (y,m),m) | (20) |
 | (21) |
Availability of software
Matlab files for implementing the algorithm, running the simulations, and generating the figures described here are available at the authors' website: http://www.mit.edu/tidor.Results
We generated 1000 data sets from 1000 random parameterized topologies and asked each of the methods to determine the relative evidence that each topology had generated the data, quantified as a probability distribution over the four candidate topologies. These probability distributions were compared to each other and, in particular, to the Monte Carlo result, which should have converged to the correct probability distribution.We show four of the thousand runs in Fig. 3 to illustrate typical results seen. The true topologies underlying Fig. 3A–D were topologies 1, 2, 3, and 4, respectively. The results for our scenario can be classified into two main cases. The less common case, represented by Fig. 3B, is the case where the data unambiguously indicate the true topology; in this case, it was topology 2. When only one topology can fit the data, with the ability to fit the data indicated by the “Likelihood” bars, then all methods agree that the topology that fits is the correct topology. The more common case is represented in Fig. 3A, C and D. Here, all the topologies can the fit the data to some degree and the different methods give different probability distributions on the data. In these cases, one can see that the likelihood method tends to overstate the true probability, given by the “Monte Carlo” bars, for topology 1, which has the greatest number of parameters. Interestingly, the AIC and SIC methods show a strong bias in favor of topology 4, which has the fewest parameters. However, it can be seen that the linearization method is quite close to the Monte Carlo method in each case, suggesting that it is a good approximation. If one were to look at just one result, for instance Fig. 3D, it may appear that the AIC and SIC are the superior methods because they are the only ones that put the highest probability on the true topology, topology 4. However, this would be misleading, because they frequently put a high probability on topology 4, even when it is not the topology that generated the data (Fig. 3A and 3C). In fact, even in Fig. 3D, they are overstating the evidence that topology 4 is true, for the actual probability is provided by the Monte Carlo.
For each of the 1000 runs, we calculated the Jensen–Shannon (JS) divergence between the probability distribution given by each method and the Monte Carlo probability distribution. The JS divergence is one standard measure of how different two probability distributions are, which in this case provides a single quantification for how far each method's answer is from the correct answer. The JS divergence returns a value between 0 (identical distributions) and 1 (non-overlapping distributions). The divergence values for each method over all runs were binned and plotted as a histogram in Fig. 4. Of the other methods, the linearization method is closest to the Monte Carlo. The likelihood comparison was the next closest, followed by the AIC and the SIC.
While the JS divergence is one measure of how different one probability distribution is from a reference distribution, it does not report numbers that can easily be used to understand if the error in each approximation is large enough to matter. To aggregate the results in a way that was easier to interpret, we took the most likely topology according to each method and compared it to the topology that actually generated the data. In the real world, we would not be able to do this test because the true topology would be unknown, but this computational scenario allows us to investigate whether the methods actually do what they are intended to do—tell us which topology is correct according to the data. We computed the fraction of top hits that were correct for each method (Fig. 5). As expected, the Monte Carlo was correct most often; the most likely topology according to this method was the true topology 46% of the time. Because Monte Carlo provides the correct probability, it is impossible to do better than this provided that the Monte Carlo has converged and a sufficiently large number of runs are done to approach statistical averages. No method could pick the correct topology 100% of the time because that information was not contained in the data. The linearization method did almost as well as Monte Carlo, finding the correct topology 44% of the time. The likelihood comparison, the AIC, and the SIC were correct 30%, 30%, and 28% of the time, respectively. Surprisingly, these heuristics only do slightly better than randomly guessing one of the four topologies, which would be correct 25% of the time.
We analyzed the bias in each method by plotting the mean probability each method returned for each topology (Fig. 6). An unbiased method will return a mean of 0.25 for each topology because that is the probability by which each topology was drawn. The bias that the likelihood comparison has for the topology with the most parameters can be seen though it is not particularly large. Interestingly, AIC and SIC are strongly biased toward the topology with the fewest parameters. The Monte Carlo method has no bias, as expected, but neither does the linearization, which is a satisfying result.
Despite the improved accuracy of linearization, the method does not take substantially greater computational resources than the heuristics, which take radically less time to compute than the full Monte Carlo. While the Monte Carlo method took a median of 13 days to complete, the linearization method, likelihood comparison, AIC, and SIC all took a median of 4.2 minutes to complete. The fast methods took the same amount of time to complete because the time of each was dominated by the time it took to simply fit parameters for each of the topologies to the data. The computation of the likelihood (needed for all methods) and the Fisher information matrix (needed for the linearization method) took about as much time as a single iteration of the gradient descent fitting algorithm. Computing the Fisher information matrix requires computing the sensitivities of the outputs to the parameters, which is not needed to compute a likelihood comparison, the AIC, or the SIC and is more expensive than simply simulating the system to compute the likelihood of the data. If the time to fit the topologies to the data is ignored, it took a median of 0.80 seconds to compute the likelihood comparison, AIC, and SIC and 3.4 seconds to compute the linearization method. Thus, the linearization was slightly more time consuming than the other fast methods, but insignificantly so.
Conclusion
The quantification of parameter uncertainty in ODE models of biological systems has a number of successful and computationally feasible methods.31,38,39,42,51 However, doing the same for the other half of the model, the topology, has not been as successful. The existing methods are either expensive (Monte Carlo methods) or inaccurate (various heuristics). We have proposed one method, our linearized Bayesian approach, which may fill this gap. It returns an answer that is similar to the Monte Carlo gold standard, but does so at a computational cost no more than fitting the topologies to data.There are several ways to interpret what the method is doing. The simplest one and the one we have used throughout this work is that it is a linearization at the maximum a posteriori parameter set, because we arrive at this parameter set with nonlinear fitting and then evaluate the likelihood, the prior, and the Fisher information matrix with these parameters. These values are then plugged into a formula that is exactly true only for linear Gaussian topologies. Another interpretation is that the integrand of the marginal likelihood equation has been replaced by a Laplace approximation. A Laplace approximation is like a second-order Taylor approximation except that an exponential of a polynomial is used rather than a polynomial itself.52 A Laplace approximation generates a single Gaussian at a point to approximate the rest of the function. This interpretation has one additional caveat: instead of the second-order derivative of the log likelihood with respect to the parameters (also known as the Hessian), we use the Fisher information matrix, which is only exactly equal to the Hessian if the model is linear. Computing the Hessian takes greater computational resources, yet has little impact on the result (data not shown). The use of the Hessian and Fisher information matrix in the Laplace approximation of marginal likelihoods even has some use in other fields.46
The number of possible topologies grows exponentially with the number of states. The linearization method would not be very effective at reverse engineering the topology from scratch because the method considers each topology individually. However, the method could work effectively as a subsequent step to other methods that efficiently pare down the vast topological space to a manageable number of topologies. As long as the number of topologies is small enough such that each can be fit to data, possibly in parallel, then the linearization method would efficiently quantify the uncertainty in the remaining set.
Because the problem is phrased in a Bayesian fashion, the probability distribution returned by the linearization method sums to 1. This means that, like all Bayesian methods, it is implicitly assumed that the true topology is in the set of possibilities. The possibility that no topology is a good fit for the data can be mitigated by checking after the fact that there is one at least one topology that fits the data by using a frequentist statistic, such as a chi-square p-value.
In this work we have demonstrated the effectiveness of the approximation only on a single set of simple biological topologies. Testing on more systems, especially more complex systems, is warranted. The main limitation with our testing scenario in evaluating the method on more complex topologies was that the Monte Carlo method already took 13 days to complete. A noticeably more complex set of topologies would not finish in a reasonable amount of time, so that there would be no gold standard with which to compare. Perhaps this illustrates why a good approximation of the topology probability is so important: most of the models that biologists care about are too large to compute the topology probability with a Monte Carlo method.
The approximation is dependent on the “area” under the hyperdimensional Gaussian being similar to the “area” under the product of the likelihood and the prior, which has the shape of the parameter posterior distribution. If the region of probable parameters is substantially larger or smaller than the approximation, the approximation will fail unless the difference is similar for all topologies. It may be interesting to note that the linear Gaussian approximation does not have to be very similar to the true distribution; it only has to have a similar integral. This may be an important property because the posterior parameter uncertainty is typically very large for biological models. When the uncertainty is large, there will be regions of likely parameter sets that a linear approximation will not recognize as likely parameters because the linear approximation is only valid for a short range. Fortunately, the linear approximation does not actually have to overlay the underlying posterior distribution in order to be a good approximation for the purpose of topology probability; it only has to have a similar integral. A case where one might expect the approximation to be very different from the true value is when the posterior is multimodal. How much of a problem this is in practice should be monitored through experience.
In our previous work, we found that a linear approximation of the parameter uncertainty was an effective enough approximation for designing experiments to efficiently reduce that uncertainty.39,42 This work does not consider the effectiveness of our approximation for any particular task, but the ability to not only determine the current topology uncertainty but design experiments to reduce that uncertainty is an alluring goal for which research is ongoing to achieve.
Funding
This research was partially funded by the National Cancer Institute of the US National Institutes of Health (U54 CA112967) and the National Research Foundation Singapore through the Singapore–MIT Alliance for Research and Technology's BioSyM research program.References
- P. Mendes, W. Sha and K. Ye, Bioinformatics, 2003, 19, ii122–ii129 CrossRef PubMed.
- J. A. Papin, T. Hunter, B. O. Palsson and S. Subramaniam, Nat. Rev. Mol. Cell Biol., 2005, 6, 99–111 CrossRef CAS PubMed.
- J. Stelling, Curr. Opin. Microbiol., 2004, 7, 513–518 CrossRef PubMed.
- A. Bensimon, A. J. R. Heck and R. Aebersold, Annu. Rev. Biochem., 2012, 81, 379–405 CrossRef CAS PubMed.
- N. S. Holter, M. Mitra, A. Maritan, M. Cieplak, J. R. Banavar and N. V. Fedoroff, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8409–8414 CrossRef CAS PubMed.
- N. S. Holter, A. Maritan, M. Cieplak, N. V. Fedoroff and J. R. Banavar, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 1693–1698 CrossRef CAS PubMed.
- W. Liebermeister, Bioinformatics, 2002, 18, 51–60 CrossRef CAS.
- J. C. Liao, R. Boscolo, Y.-L. Yang, L. M. Tran, C. Sabatti and V. P. Roychowdhury, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 15522–15527 CrossRef CAS PubMed.
- E. P. Gianchandani, J. A. Papin, N. D. Price, A. R. Joyce and B. O. Palsson, PLoS Comput. Biol., 2006, 2, e101 Search PubMed.
- I. Famili and B. O. Palsson, J. Theor. Biol., 2003, 224, 87–96 CrossRef CAS.
- M. B. Eisen, P. T. Spellman, P. O. Brown and D. Botstein, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 14863–14868 CrossRef CAS.
- S. Raychaudhuri, J. M. Stuart and R. B. Altman, Pac. Symp. Biocomput., 2000, 455–466 CAS.
- K. Sachs, S. Itani, J. Carlisle, G. P. Nolan, D. Pe'er and D. A. Lauffenburger, J. Comput. Biol., 2009, 16, 201–212 CrossRef CAS PubMed.
- J. Tegnér, M. K. S. Yeung, J. Hasty and J. J. Collins, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5944–5949 CrossRef PubMed.
- A. Julius, M. Zavlanos, S. Boyd and G. J. Pappas, IET Syst. Biol., 2009, 3, 155–166 CrossRef CAS PubMed.
- K. Selvarajoo and M. Tsuchiya, in Introduction to Systems Biology, ed. S. Choi, Humana Press, 2007, pp. 449–471 Search PubMed.
- E. August and A. Papachristodoulou, BMC Syst. Biol., 2009, 3, 25 CrossRef PubMed.
- K. Sachs, O. Perez, D. Pe'er, D. A. Lauffenburger and G. P. Nolan, Science, 2005, 308, 523–529 CrossRef CAS PubMed.
- M. K. S. Yeung, J. Tegnér and J. J. Collins, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6163–6168 CrossRef CAS PubMed.
- V. Vyshemirsky and M. A. Girolami, Bioinformatics, 2008, 24, 833–839 CrossRef CAS PubMed.
- R. E. McCulloch and P. E. Rossi, Biometrika, 1992, 79, 663–676 CrossRef PubMed.
- M. A. Newton and A. E. Raftery, J. R. Stat. Soc. Series B Stat. Methodol., 1994, 56, 3–48 Search PubMed.
- R. Neal, The harmonic mean of the likelihood: Worst Monte Carlo method ever, 2008 Search PubMed.
- B. Calderhead and M. Girolami, Comput. Stat. Data Anal., 2009, 53, 4028–4045 CrossRef PubMed.
- X.-L. Meng and W. H. Wong, Stat. Sin., 1996, 6, 831–860 Search PubMed.
- N. Lartillot and H. Philippe, Syst. Biol., 2006, 55, 195–207 CrossRef PubMed.
- N. Friel and A. N. Pettitt, J. R. Stat. Soc. Series B Stat. Methodol., 2008, 70, 589–607 CrossRef PubMed.
- A. Gelman and X.-L. Meng, Stat. Sci., 1998, 13, 163–185 CrossRef.
- R. Neal, Stat. Comput., 2001, 11, 125–139 CrossRef.
- P. J. Green, Biometrika, 1995, 82, 711–732 CrossRef PubMed.
- T. Toni, D. Welch, N. Strelkowa, A. Ipsen and M. P. H. Stumpf, J. R. Soc. Interface, 2009, 6, 187–202 CrossRef.
- T.-R. Xu, V. Vyshemirsky, A. Gormand, A. von Kriegsheim, M. Girolami, G. S. Baillie, D. Ketley, A. J. Dunlop, G. Milligan, M. D. Houslay and W. Kolch, Sci. Signal., 2010, 3, ra20 Search PubMed.
- D. Posada and T. R. Buckley, Syst. Biol., 2004, 53, 793–808 CrossRef PubMed.
- A. Raftery, Am. Sociol. Rev., 1986, 51, 145–146 CrossRef.
- H. Akaike, Bull. Int. Stat. Inst., 1983, 50, 277–291 Search PubMed.
- G. Schwarz, Ann. Stat., 1978, 6, 461–464 CrossRef.
- K. P. Burnham and D. R. Anderson, Model selection and multi-model inference: a practical information-theoretic approach, Springer, 2002 Search PubMed.
- R. N. Gutenkunst, J. J. Waterfall, F. P. Casey, K. S. Brown, C. R. Myers and J. P. Sethna, PLoS Comput. Biol., 2007, 3, e189 Search PubMed.
- J. F. Apgar, D. K. Witmer, F. M. White and B. Tidor, Mol. BioSyst., 2010, 6, 1890–1900 RSC.
- R. Chachra, M. K. Transtrum and J. P. Sethna, Mol. BioSyst., 2011, 7, 2522–2522 RSC.
- D. R. Hagen, J. F. Apgar, D. K. Witmer, F. M. White and B. Tidor, Mol. BioSyst., 2011, 7, 2523–2524 RSC.
- D. R. Hagen, J. K. White and B. Tidor, Interface Focus, 2013, 3, 20130008, DOI:10.1098/rsfs.2013.0008.
- J. Kuha, Sociol. Methods Res., 2004, 33, 188–229 Search PubMed.
- D. L. Weakliem, Sociol. Methods Res., 1999, 27, 359–397 Search PubMed.
- J. E. Ferrell and R. R. Bhatt, J. Biol. Chem., 1997, 272, 19008–19016 CrossRef CAS PubMed.
- A. E. Raftery, Biometrika, 1996, 83, 251–266 Search PubMed.
- C. Evans, J. Noirel, S. Y. Ow, M. Salim, A. G. Pereira-Medrano, N. Couto, J. Pandhal, D. Smith, T. K. Pham, E. Karunakaran, X. Zou, C. A. Biggs and P. C. Wright, Anal. Bioanal. Chem., 2012, 404, 1011–1027 CrossRef CAS PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS PubMed.
- W. K. Hastings, Biometrika, 1970, 57, 97–109 CrossRef.
- G. O. Roberts and J. S. Rosenthal, Stat. Sci., 2001, 16, 351–367 CrossRef.
- C. Kreutz and J. Timmer, FEBS J., 2009, 276, 923–942 CrossRef CAS PubMed.
- R. E. Kass, L. Tierney and J. B. Kadane, Contemp. Math., 1991, 115, 89–99 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4mb00276h |
| This journal is © The Royal Society of Chemistry 2015 |