Modeling and CFD simulation of nutrient distribution in picoliter bioreactors for bacterial growth studies on single-cell level

Abstract

A microfluidic device for microbial single-cell cultivation of bacteria was modeled and simulated using COMSOL Multiphysics. The liquid velocity field and the mass transfer within the supply channels and cultivation chambers were calculated to gain insight in the distribution of supplied nutrients and metabolic products secreted by the cultivated bacteria. The goal was to identify potential substrate limitations or product accumulations within the cultivation device. The metabolic uptake and production rates, colony size, and growth medium composition were varied covering a wide range of operating conditions. Simulations with glucose as substrate did not show limitations within the typically used concentration range, but for alternative substrates limitations could not be ruled out. This lays the foundation for further studies and the optimization of existing picoliter bioreactor systems.

---

1. Introduction

Microfluidic single-cell growth analysis of bacteria has potential to influence many fields, among them industrial biotechnology, by introducing new ways to examine organisms.¹ Consequently there has been an interest in fabrication, operation, and design of microfluidic single-cell devices.² In the last years progress in fabrication has led to various configurations of chambers, boxes, channels and traps in devices mostly made from polydimethylsiloxane (PDMS).^3,4

Whereas mass transport within lab-scale cultivation devices is characterized rather well, characterization of microfluidic single-cell systems has only become of interest recently. Especially the transport of nutrients and metabolic products has not been given a lot of attention. First studies were reported analysing oxygen transport through PDMS systems.⁵ It is often assumed that the nutrient distribution is constant and sufficient for cell growth across the chambers, especially for solutes like glucose.⁶ Studies have shown that for small cell traps and channels this holds true, but for larger colonies this has not yet been investigated in detail.^7,8 Here, we focus for the first time on the characterization of nutrient availability within larger colonies (≥80 cells), as they are often found in bacterial single-cell studies.^1,9

1.1 Microfluidic single-cell cultivation

The field of microfluidics encompasses the manipulation and analysis of fluids within micrometer-sized structures.² The physics of small volumes and length scales dictate laminar flows and mixing by diffusion, which is very different from the turbulence and advection dominated mass transfer in macroscopic devices.¹⁰

Different microfluidic devices have been reported to facilitate and offer new possibilities for the investigation of industrially relevant bacteria and applied to different organisms like Corynebacterium glutamicum or Escherichia coli.^9,11–16 A category of those devices is characterized by semi-continuous or continuous operation, also called microchemostat, and two-dimensional growth of the bacterial cultures. The exact design can vary for different versions, but all share most features. Every device contains several hundred cultivation chambers, each able to grow microcolonies of up to several hundred cells stemming from a single cell. The chamber dimensions vary between 40 μm × 40 μm × 1 μm and 60 μm × 60 μm × 1 μm.^11–16 The chamber height of 1 μm restricts the cell cultures to grow in a monolayer and therefore allows for automatic quantitative analysis using microscopes. The cultivation chambers are connected to two channels which are perfused with growth medium. In this way fresh substrate is supplied to the cells and metabolic products and waste are removed. The channels are typically 10 μm deep and 30 μm wide.¹⁷

The studied micro-devices allow to observe single microorganisms and investigate population heterogeneity due to genetic differences, stochastic effects, population based phenomena and environmental heterogeneity. The latter is especially important for the scale-up of processes from laboratory to industrial scale since insufficient mixing in large bioreactors causes individual cells to experience varying and changing environmental conditions. The length scales in microfluidic cultivation devices are in the order of magnitude of organisms or below, so that it is possible to precisely manipulate single cells and control their environment. That enables researchers to grow cells on a defined medium or apply fast temperature and medium changes to simulate conditions in macroscopic devices.¹⁸ The use of automated time-lapse microscopy for many growth chambers in parallel in combination with genetically encoded fluorescence reporters enables the generation of statistically trustworthy data, the study of rare events and derivation of lineage information, for example with software visualization tools such as “Vizardous”.^1,19 Past applications included the investigation of the growth-enhancing effect of protocatechuic acid (PCA) for C. glutamicum¹³ and light-responsive control of bacterial gene expression in E. coli.¹⁵

1.2. Scope of this study

Until now to the best of our knowledge only rough estimates of the mass transfer within recently developed chips have been made. The small volumes in picoliter range make it challenging to measure concentrations of metabolites. Measuring concentrations within the reaction chambers has been done for other substances and in bigger systems⁵ but not yet for picoliter bioreactors. Existing CFD simulations mostly focus on the velocity field, either static²⁰ or dynamic with bacterial movement, for example to optimize cell trapping and seeding.^9,21 Some include the analysis of concentration profiles around a single cell.^7,22 However, it remains unclear how strongly cellular behaviour is influenced by environmental chemical gradients within larger microfluidic cultivation chambers and cell colonies. Mather et al. for example have observed different cell sizes within growth chambers of dimensions up to 200 μm × 2000 μm × 1 μm and explained this observation with locally varying concentrations of nutrients and byproducts. This effect could also be explained by shape adaption due to increase in pressure of neighbour cells.⁹

The main objective of this study was to create a computational model that can answer questions regarding the mass transfer in the system during operation. For doing so, the fluid velocity field and the mass transfer of solutes, by diffusion and advection, had to be calculated. The model was then used to further evaluate if the transport of substrates from the channels into the growth chambers is fast enough, if the metabolic products get washed out or accumulate, and if there are significant differences in conditions between the medium in the chambers and the channel. The impact of colony size and the sensitivity of organism performance towards parameters like substrate concentration in the medium, and the uptake and production rates of single cells was also investigated. Focus of the study was the investigation of limitations within colonies, rather than selected single cells. Therefore biological heterogeneity has not been considered and the current model for the cell metabolism only reproduces average cell behaviour and ignores effects like substrate inhibition or cell maintenance, which might also have an influence on the investigated system. While this simplification and the range of parameters and operating conditions make it impossible to reproduce many experimental observations by computer simulation, they do enable the investigation of environmental heterogeneities and the influence of the chip design on their formation. These simulations lay the foundation to optimize single-cell bioreactors and create a deeper understanding of mass transfer and nutrient availability within cell colonies and cell clusters.

2. Model

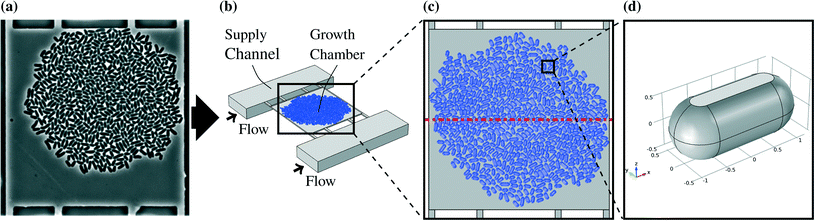
The model of the observed system was created by virtually separating the chip and the organisms from the environment by defined connections and thereby disassembling the system into distinct interconnected parts. Fig. 1b shows the three-dimensional representation of one growth chamber with a colony inside and the adjacent supply channels. A more detailed description can be found in Appendix A.1.

Fig. 1 (a) Microscopic picture of a real colony in a chamber, (b) three-dimensional representation of one growth chamber with cell colony (in blue) and adjacent supply channels, (c) large colony model as a whole, the red dash dotted line indicates the plane of symmetry, (d) single cell model, the flat space shows where the cell is in direct contact with the chamber ceiling.

A basic modeling assumption was that the conditions in each growth chamber are independent of the chamber's position on the chip (see Appendix A.2). The supply channels between the chambers are continuously flushed with fresh growth medium so that changes over the length of the channel can be neglected. Estimations of metabolic production and uptake rates with the maximal chip size have shown that this assumption is justified for most substrate concentrations and uptake rates (data not shown). Therefore it was sufficient to model one chamber with the adjacent channels in detail. The mass transfer of glucose and PCA takes place in the fluid within the chambers and in the channels. The highest solute concentration encountered was the one of glucose with 222 mmol L⁻¹ and therefore all solutes could be neglected in the calculation of the liquid velocity field. The mass transfer equations for the solutes were solved separately after solving the Navier–Stokes equations for the velocity field.

The model was solved using COMSOL Multiphysics 4.4. The mesh was created using the free tetrahedral option. This resulted in 626 541 elements for the model with the large colony. A finer mesh with 2 002 761 elements did not show significant differences for the solution so that the element size was assumed to be sufficiently small. The geometry of the model is symmetric if the cell colony is viewed as homogeneous, and other chambers connecting to the supply channels are neglected due to the low uptake and production rates of a colony compared to the mass flow in the supply channels. Therefore the number of elements could be further reduced to 353 051. The symmetry plane is indicated by the red dashed lines in Fig. 1c and 3. Quadratic functions were used for the concentrations and velocity and linear functions for the pressure.

2.1. Fluid dynamics

The velocity field was calculated in steady state because the chip is operated under constant conditions for long times. Eqn (1a) and (1b) show the Navier–Stokes equations used for the model.

ρu·∇u = −∇p + μ∇²u (1a)

∇·u = 0 (1b)

Here u denotes the velocity vector, ∇ is the gradient operator, ρ the density, p the pressure and μ the viscosity.²³ The chip is operated close to atmospheric pressure and at 303.15 K for the cultivation of C. glutamicum. All height differences in the model are very small, so that gravitational force was neglected. The fluid within the channels and chambers is the medium CGXII or a similar liquid. It consists of water with up to 4% glucose and other nutrients.¹³ Since the other nutrients are supplied in smaller amounts and the properties of pure water are very similar to water with glucose, the liquid was modeled isothermal, incompressible, and Newtonian with the density and viscosity of water. The density of water ρ is 995.6 kg m⁻³ and the viscosity μ is 7.97 × 10⁻⁴ Pa s.²⁴

The flow into the channel from upstream is given approximately by the average velocity in channel direction. The channel was modeled for 30 μm in front of the first chamber inlet to allow formation of the parabolic velocity profile and thereby negate entrance effects. The average inlet velocity was calculated from the flow rate divided by the channel cross section. This led to an average inlet velocity of 1.11 × 10⁻³ m s⁻¹ for the flow rate of 200 nL min⁻¹.

Pressure was used as outlet boundary condition and it was set to 0 Pa. This means the calculated pressures are in relation to the unknown pressure at that point. The operating pressure is not significantly different from the atmospheric pressure and therefore no additional information about the system could be gained from the absolute value. The PDMS and glass walls were assumed to be impermeable to the liquid and the no-slip condition was used.²⁵

2.2. Mass transfer

Fick's law of diffusion and binary aqueous diffusion coefficients were used for the mass transfer calculations. This is possible because glucose has with a maximum of 222 mol m⁻¹ by far the highest concentration of solutes in the chamber liquid. In this concentration it is safe to assume each glucose molecule mainly interacts with water. Eqn (2) is the resulting instationary conservation equation for each of the solutes i.²³Here c_i denotes the concentration of each species and D_i the binary diffusion coefficient of the substances i in water. u is the velocity profile which was previously calculated using eqn (1). Eqn (2) was solved time dependent, because the inlet concentrations were changed from zero to 100% in a step change at the beginning of the simulation. The time until steady state was calculated to give an indication of how fast the conditions in the chambers can be changed during operation.

The concentrations of substances at the inlets were set to the ones in pure growth medium in accordance with the assumption that the changes of concentration over the length of the supply channels can be neglected. The inlet concentrations for the two substrates glucose and PCA were varied, for glucose from 41.91 mmol L⁻¹ to 222.02 mmol L⁻¹ and for PCA from 0.195 mmol L⁻¹ to 1.95 mmol L⁻¹. In the case of glucose it can be assumed that no substrate inhibition takes place.²⁶

The relation between the advective mass transfer and the diffusive mass transfer can be expressed by the Péclet-number Pe. The value for the supply channels is above 10, so that at the outlet the diffusive mass transfer can be neglected in comparison to the advective mass transfer.²³ It was assumed that glass and PDMS are impermeable for the observed solutes and absorption can be neglected. The diffusion coefficients used are reported in Table 1.

Table 1 Diffusion coefficients in water at 30 °C in 10⁻¹⁰ m² s⁻¹

Solute	Diffusion coefficient	Publication
Glucose	5.4	Gladden and Dole^27
Lactic acid	11.2	Ribeiro et al.^28
PCA	2.8	Srinivas et al.^29

---

2.3. Microorganisms

The microorganism used in this work is the bacterium C. glutamicum. The research conducted with the modeled microfluidic device has mainly been focused on this organism. Cells generally do not allow free diffusion of all substances through their membranes. This implies that the cells in the chambers reduce the liquid volume available for mass transfer and block the direct diffusion paths, especially for molecules like sugars and amino acids.³⁰

The cells were designed as cylinders with spherical domes at both ends. The radii of the cylinders and the domes were chosen to be 530 nm while the cultivation chamber has a height of 1 μm. That represents cells with flexible walls which touch the floor and the ceiling of the chamber. The different cell sizes in real colonies were represented by three different lengths of 3.16 μm, 2.36 μm, and 1.91 μm. Those cell lengths were chosen to be close to the values observed in experiments.¹³ A single cell model is shown in Fig. 1d. Two different representative colony sizes were implemented as models, referred to as large colony and small colony. The large colony, which is shown in Fig. 1c, takes up most of the chamber and consists of around 600 cells, while the small colony consists of circa 80 cells which are located in the chamber center. The cells were positioned manually based on a snapshot of a real experiment. An example picture of a real colony in a chamber is shown in Fig. 1a.

The cell metabolism was modeled by the Monod kinetics. The Monod equation is similar to the Michaelis–Menten enzyme kinetic and has been used as empirical model for the behavior of cell populations. The basic assumption is that one enzymatic reaction is a limiting step in the cellular reaction network and therefore the whole cell follows similar dynamics. It is expressed by the following equation:³¹

Here Upt_i is the uptake of substance i, depending on the substrate concentration c_i, the maximum uptake rate Upt^max_i and the Monod constant K_i. Eqn (3) was evaluated locally, therefore the uptake rate on a point of the surface of a cell body depends on the concentration c_i at this point where the flow is evaluated. This means the metabolic rates could vary over the surface of a cell, depending on the available concentrations. The model for the microorganisms is connected to the mass transfer model described in section 2.2 by using the Monod equation given in eqn (3) as boundary condition for eqn (2) on the cell surfaces.

The values of K_i were given with 4.5 mmol L⁻¹ for glucose³² and estimated as 0.1 mmol L⁻¹ for PCA.¹³ The uptake rates taken from literature were between 0.414 μmol g_CDW⁻¹ s⁻¹ (ref. 33) and 2.08 μmol g_CDW⁻¹ s⁻¹ (ref. 34) for glucose and at 0.622 μmol g_CDW⁻¹ s⁻¹ for PCA.¹³ Those values had to be converted from cell dry weight (CDW) to single-cell production rates. The cell dry weight for a single cell calculated from values found in literature varied up to the factor 13.7.^13,35,36 Therefore the simulation was conducted for a range of rates. The upper and lower bound of those rates are shown in Table 2.

Table 2 Metabolic uptake rates in mol s⁻¹ m⁻²

Substrate	Low rate	High rate
Glucose	1.65 × 10^−8	1.14 × 10^−6
PCA	2.49 × 10^−8	3.41 × 10^−7

---

C. glutamicum has been observed to produce organic acids with a yield of up to 1.99 mol mol⁻¹.³⁷ Lactic acid is one of those organic acids. If the complete glucose uptake was used to produce lactic acid, the maximum yield would be 2 mol mol⁻¹. Lactic acid production was used as an example to represent a solute which is produced in high amounts and could theoretically accumulate to high concentrations within the growth chambers. The production rate of lactic acid was approximated as two times the uptake rate of glucose converting one glucose molecule into two lactic acid molecules.

3. Materials and methods

3.1. Strain and cultivation conditions

C. glutamicum ATTC 13032 was used as model organism within this study, because it was used for single-cell growth studies in several previous studies.^14,16,38 The cultivation medium was CGXII containing the following per liter of distilled water: 20 g (NH₄)₂SO₄, 1 g K₂HPO₄, 1 g KH₂PO₄, 5 g urea, 13.25 mg CaCl₂·2H₂O, 0.25 g MgSO₄·7H₂O, 10 mg FeSO₄·7H₂O, 10 mg MnSO₄·7H₂O, 0.02 mg NiCl₂·6H₂O, 0.313 mg CuSO₄·5H₂O, 1 mg ZnSO₄·7H₂O, 2 mg biotin and 192.12 mg citric acid. The concentration of glucose was varied during growth studies in the range of 41.91 mmol L⁻¹ to 222 mmol L⁻¹. For growth studies on sole PCA as carbon source a PCA concentration of 0.0195 mmol L⁻¹ was used.

3.2. Microfluidic single-cell cultivations

The microfluidic system as described in section 1.1 was used in this study (see also Appendix A.1). For chip fabrication details and further information the reader is referred to the publications of Grünberger et al.^17,39 The microfluidic chip was mounted onto a motorized inverted microscope (Nikon Eclipse Ti, Nikon microscopy, Germany) equipped with an incubator for temperature control. The cell suspension with an OD₆₀₀ between 0.5 and 1, transferred from the pre-culture at exponential growth phase, was infused into the chip to inoculate the microfluidic cultivation chambers with single cells. Growth medium was infused at approx. 200 nL min⁻¹ after cell inoculation. CGXII medium was prepared as described before and additionally sterile filtered to prevent particle agglomeration during microfluidic cultivation. Time-lapse phase contrast microscopy images of the growing microcolonies were recorded every 10 min over 24 h of microfluidic cultivation. Afterwards, the cumulative cell area over time of the colonies was derived by ImageJ. Colony growth rates were estimated according to Grünberger et al.³⁸

4. Results and discussion

The main question investigated in this study was if there are any substrate limitations or product accumulations in the growth chambers, or if optimal conditions can be maintained over time for different substrate concentrations in the growth medium and the whole range of metabolic uptake and production rates. It is an important condition for the use of the device that enough substrate reaches the cells in the chambers and the produced solutes diffuse out through this perfusion system. Only then the cells grow with neither limitations nor product inhibitions.

In every calculation the steady state of the concentrations was reached within 30 s after the beginning of the simulation, so that it can be assumed that the concentrations within the chambers are close to their steady state values.

4.1. Velocity field

The simulated velocity field shows the highest fluid velocities in the center of the supply channels (up to 2.02 × 10⁻³ m s⁻¹) where a parabolic velocity profile was formed, while the liquid in the chamber itself moved two orders of magnitude slower with less than 2.02 × 10⁻⁵ m s⁻¹. The Reynolds number (Re), the ratio of inertial to viscous forces in a fluid, within the supply channels was determined to be Re = 0.02 and therefore allows the assumption of laminar flow (eqn (1)) or even Stokes flow. The Péclet number (Pe), the ratio of advective to diffusive mass transfer, was Pe = [scr O, script letter O](10) in the channels and Pe = [scr O, script letter O](0.1) and lower in the chambers.

As a result advective transport dominated in the supply channels while diffusion had a high importance within the chamber. Fig. 2 shows the velocity profile in the channels and in the chamber. The plane showing the velocity profile in (a) is halfway between the bottom and the top of the chamber, so that the maximum velocity in the supply channels cannot be seen.

Fig. 2 Velocity profiles: (a) Liquid velocity halfway between the bottom and the top of the chamber. (b) Velocity profiles in the supply channels. (c) Scale for velocities in m s⁻¹.

4.2. Solute distribution

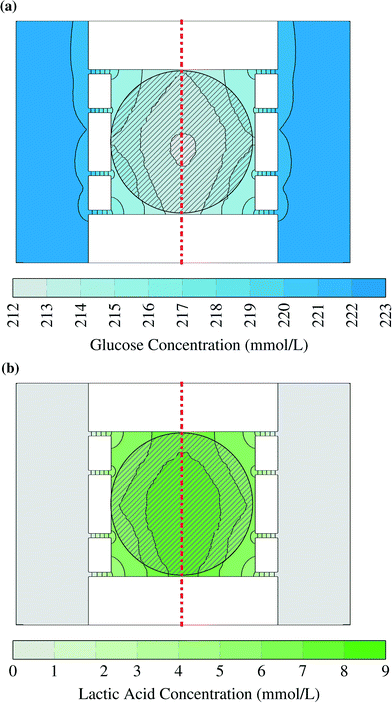
Two examples for concentration distributions in steady state are shown in Fig. 3. These results were calculated using the maximum uptake rates assumed in this study (Table 2) and the large colony, which is indicated by the circular grey striped area. A gradient can be observed from the chamber center to the supply channels. The concentration has been plotted as interpolated surface over the concentrations in the horizontal plane at half the height of the chamber in the liquid volumes between the cells. The cells have been omitted from the picture to simplify reading the plot. The small advective mass transfer caused by low liquid velocity inside of the chambers allowed the formation of the gradient which generated diffusive flow. The concentration in the supply channels was close to the supplied medium concentration because there the liquid velocity was fast and fresh medium continuously entered the channel.

Fig. 3 Glucose (a) and lactic acid (b) concentrations in picoliter bioreactor. The striped area indicates the position of the bacterial colony, while the dash dotted line shows plane of symmetry. The cells have been omitted from this picture. The flow enters the supply channels from the lower end of the figure.

Glucose concentrations within the simulated range did not lead to any inhibition. This can be seen in Fig. 3a: the concentrations in the chamber center did not drop below 212 mmol L⁻¹ and therefore the uptake rates were practically independent of the local substrate concentration. The gradient was smaller for lower glucose uptake rates and smaller cell colonies. Even for worst case conditions, which are the lowest glucose concentration (41.91 mmol L⁻¹) and the highest uptake rate (1.14 × 10⁻⁶ mol s⁻¹ m⁻²), the cells in the middle of the center of the large colony reached uptake rates above of 97% of the ones in pure growth medium. These results show that it is reasonable to assume cells within the microfluidic device do not experience any glucose limitation.

The lactic acid concentration reached up to 9 mmol L⁻¹. Lactic acid was used to represent a product with a very high production rate. Therefore the results can be used as upper bound for any product as long as it has a similar diffusion coefficient. With a smaller diffusion coefficient the gradient will grow as the product flow from the cells stays constant in the model. The effect of this concentration depends on the toxic and inhibitory strength of the product and therefore has to be evaluated case-by-case.

The concentrations in the growth chamber were heavily dependent on the size of the colony and the metabolic rates simulated. The points for which the concentrations or metabolic rates are shown in the following diagrams are indicated by red “x” in Fig. 4. Fig. 4c shows lactic acid concentrations for varying distances from the chamber center. The colony size and the metabolic production rates were varied. While the product concentrations for low rates (continuous lines) were very small and unlikely to affect cell behavior, they were much higher for high rates (dash-dotted lines). The colony size also had a significant effect, so that the concentrations were much lower for high rates and the small microcolony (dash-dotted black line) than for the large microcolony (dash-dotted red line).

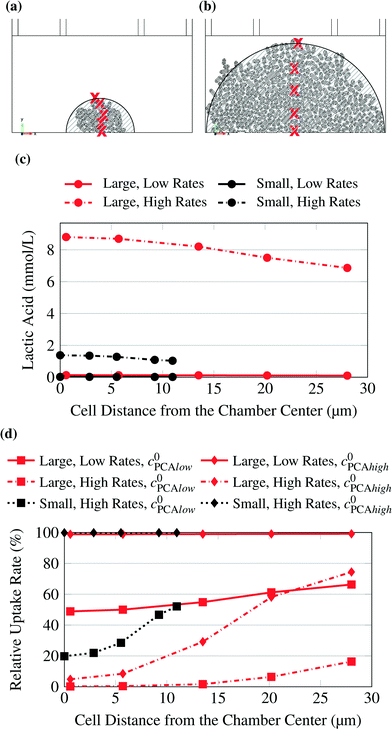Fig. 4 Small (a) and large (b) microcolony. Studied points indicated by red “x”. The striped areas are shown for comparison with Fig. 3. (c) Lactic acid concentration at selected points. The concentration was calculated for varying uptake rates and for small and large microcolonies. (d) PCA uptake rate at selected points. The uptake rate was calculated for varying inlet substrate concentrations (C⁰_PCAlow = 0.195 mmol L⁻¹, C⁰_PCAhigh = 1.95 mmol L⁻¹) and for small and large microcolonies.

The same calculations as for glucose were also conducted with PCA as substrate, which was supplied in much smaller concentrations. Here, depending on colony size and uptake rates, limitations were observed. Fig. 4d shows the relative uptake rate of PCA for several cells with varying distance from the chamber center.

Eqn (4) shows how the relative uptake rate was calculated for each studied cell by dividing the average uptake of substrate i over the cell's surface, , by the maximal uptake rate allowed for the growth medium substrate concentration c_i using the Monod kinetics. If a cell has a relative uptake rate significantly lower than 100% there are concentration differences within the growth chamber which lead to inhomogeneous conditions for the cells.

It is important that a relative uptake rate of 100% does not imply maximal growth rate. The growth rate is determined by the Monod kinetic for a certain concentration. The relative uptake rate shows how close the cell comes to experiencing the concentrations of pure growth medium. This makes it easier to evaluate if the conditions are homogeneous across the whole colony and the concentration gradients are small across the chambers. In cases of strong substrate limitations further investigations are required since the Monod kinetic does not include cell maintenance.³⁰ Differences are also caused by the fact that the modeled colony size was static while a real colony would not necessarily grow to a similar size under limiting conditions.

The low uptake rates at the higher PCA concentration of 1.95 mmol L⁻¹ created homogeneous conditions across the chamber for both colony sizes, while higher rates or lower substrate concentrations caused significant gradients up to severe limitations in the center of the colony. Consequently, it is recommended to use experimental data only from small colonies. If the colony grows too big it is likely that product accumulation has an effect on the cells in the center. Also the cells in the inner area of the colonies could experience significantly different product and substrate concentrations from the ones on the border and therefore the conditions would be inhomogeneous. Further the conditions within the colony could be quite homogeneous but the concentration far below the growth medium concentration.

5. Experimental validation

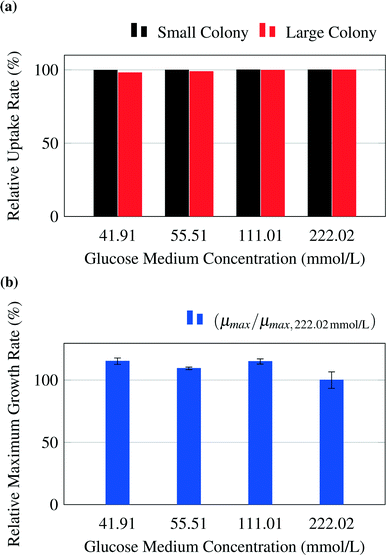
The model predicts no limitations for glucose concentrations in the range from 41.91 mmol L⁻¹ to 222.02 mmol L⁻¹ (Fig. 5a). To confirm this prediction, experiments were performed for the chosen glucose concentrations. The experimental results are shown in Fig. 5b and confirm the results. A constant maximum growth rate μ_max was observed for colony sizes from ca. 10 up to more than 300 cells (data not shown). This gives a strong indication that all cells within the colony grew with the same maximal growth rate, which is consistent with the model's prediction of no significant concentration gradients within the growth chambers. The slightly increased growth rates measured at lower glucose concentrations could potentially be the result of substrate inhibition, which is not included in the present metabolic model and is currently under further experimental investigation.

Fig. 5 (a) Average relative uptake rate for glucose of the whole colonies calculated by the model. (b) Experimental results for growth rates μ_max of whole colonies normalized to growth rate at glucose concentrations of 222.02 mmol L⁻¹, μ_{max,222.02 mmol L⁻¹}.

As an example for limiting nutrient conditions, the model was validated with experimental results from literature (see Unthan et al.¹³) and supporting experiments. Unthan et al. investigated the growth rate for microcolonies with PCA as single carbon source. They found a growth rate near 0.2 per hour for a PCA concentration of 0.195 mmol L⁻¹ and a growth rate near 0.3 per hour for a PCA concentration of 1.95 mmol L⁻¹.¹³Fig. 6a shows the relative uptake rates predicted by the model and the relative maximum growth rate μ_PCA/μ_max,PCA measured by Unthan et al. The model predicts for both the small and large colony strong gradients in PCA concentrations as seen in Fig. 4d leading to smaller overall colony growth rates (black and red bars in Fig. 6a). The experimental results confirm these findings (reduced colony growth rates, see blue bars) but strongly depend on the used concentration, cultivation time and maximum colony size used for growth rate determination (data not shown). The reduced colony growth rates could be due to limiting conditions, which would be in line with the models predictions, or caused by homogeneously reduced single-cell uptake rates across the colony or a combination of both. Fig. 6b shows a typical colony grown on 0.0195 mmol L⁻¹ PCA. The growth rates of two individual cell lines on different positions within a cell colony were monitored over time (see Fig. 6c and d). The cell in the center of the colony (orange) showed a different growth behaviour compared to the cell located at the border of the colony (green). At the beginning (0 h to 18 h), the cell in the center divides in continuous intervals indicating no nutrient limitations. After 18 hours the cell lineage shows reduced growth and division activity indicating nutrient limitations. After approximately 40 hours, the cell stops growing, indicating nutrient depletion in the inner area of the colony. These findings are in strong agreement with the gradient formation predicted by the computational model.

Fig. 6 Validation of growth on PCA as carbon source: (a) average relative uptake rate for PCA calculated by the model and experimental results for growth rates μ_PCA of whole colonies normalized to growth rate at PCA concentrations of 1.95 mmol L⁻¹, μ_max,PCA, from Unthan et al.¹³ (b) Image sequence of exemplary colony cultivated at 0.0195 mmol L⁻¹ PCA. The position of observed cells is indicated by a green circle for the cell of Fig. 6c and an orange square for the cell of Fig. 6d. (c) Cell length over time for a cell at the border of the observed colony, (d) cell length over time for a cell inside the observed colony. The sudden decreases in cell length indicate single-cell divisions. After approx. 23 h cells within the inner parts of the colony (orange square) show reduced growth. After 44 h many cells stop growth completely.

The simulation results are qualitatively validated by these observations. Product concentrations, for example for lactic acid, have not been measured yet. However, the model provides an estimate for the highest possible product concentration.

6. Conclusions

The purpose of this project was to create a computational model of nutrient transport within recently published single-cell bioreactors.¹⁷ Main focus was the investigation of potential nutrient limitations and the effect of inhibitory byproducts. No limitation could be found for glucose in standard concentrations even for the worst case scenario with the lowest substrate concentration (41.91 mmol L⁻¹) and highest uptake rate (Table 2). Lower substrate concentrations, for example 1.95 mmol L⁻¹ PCA, did lead to limiting conditions for some scenarios. Phenomena observed in experiments like growth limitation for cells within big colonies or no visible concentration gradients across small colonies could be recreated in the computational model with the chosen modeling assumptions. The product accumulation was simulated with very high yields and metabolic rates representing the worst case scenario. The importance of product accumulation within the chambers has to be decided case-by-case depending on the toxic or inhibitory strength. So far the high variability of the metabolic rates for single cells caused significant variations of the concentration profiles. The better understanding gained by this study enables improvements of future design and operation of picoliter bioreactors.

A. Appendices

A.1. Chip design

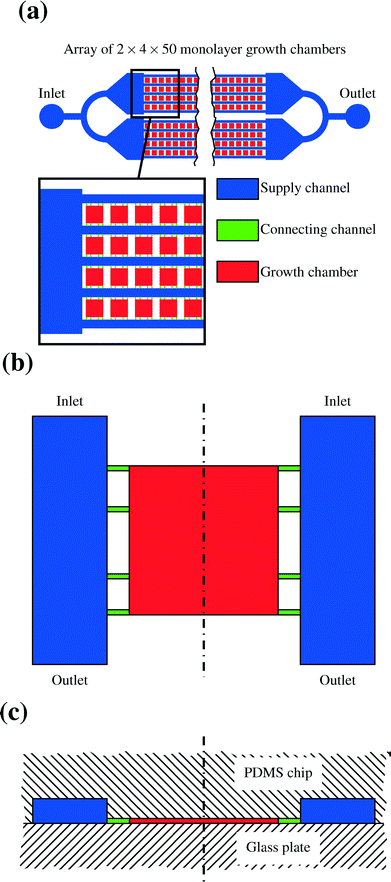
The lab-on-a-chip system's main part consists of a PDMS structure which is manufactured using the technology of soft lithography. The PDMS is usually cut into a rectangular shape. One side contains the structures which form the channels and chambers of the device as indentations. This side is surface bonded onto a thin glass plate so that the chambers and channels are completely enclosed by glass and PDMS. The basic geometry of the resulting network as it is modeled in this study can be seen in Fig. 7. Fig. 7a gives an overview over the whole array of cells, Fig. 7b shows a single chamber from above and Fig. 7c provides a side view. There are four different arrays of channels, each of them consisting of two times five channels. Between those channels there are 50 chambers in each row. The circular shapes on the outlying ends of the array are the points for connections to the syringe pumps and the collecting vessel for the effluents.¹⁷

Fig. 7 Basic geometry of a lab-on-a-chip device. (a) Shows a complete cell array, (b) a single chamber from above and (c) a side view with the position of PDMS chip and glass plate indicated. The dash dotted line shows the line of symmetry.

A.2. Influence of chamber position on chip

One modeling assumption is that the medium concentrations in the supply channels do not depend on the position of the chamber on the chip. Then the results for the first chamber are valid for all chambers. This assumption is only justified if the chip is not too big and the substrate concentration is not too low, since every cell takes up substrate and secretes products. These metabolic flows change the concentrations in the supply channels. Hence, the influence of a cultivation chamber on the other chambers further downstream was estimated using a simplified mass balance. Here a common chip design, as it is shown in Fig. 7, with four parallel rows of chambers and five channels is taken as basis. The maximum uptake of whole colonies were calculated from the parameters introduced in Table 2. The average concentration of a substance C(x) in each of the five channels after x colonies in each of the four rows can be calculated using the following equation:Production rates of secreted substances are interpreted as negative uptake rates. For this estimation it is assumed that all the cells work with their maximum metabolic rates. Upt^Total is the sum of the single-cell uptake rates for one chamber. The cross section of a channel is A = 10 μm × 30 μm. C₀ is the pure medium concentration of a substance.

The maximal uptake rate for the large colony for glucose Upt^Total is 4.78 × 10⁻¹⁵ mol s⁻¹. The initial concentration of glucose C₀ is between 41.91 mmol L⁻¹ and 222.02 mmol L⁻¹. The maximum number of chambers in a row x is 50. The average liquid velocity in the supply channels v_in is 1.11 × 10⁻³ m s⁻¹. For the lowest initial glucose concentration the average concentration in the channels is lowered from 41.91 mmol L⁻¹ to 41.34 mmol L⁻¹ after 50 chambers. A similar calculation for the product showed a maximum accumulation of 1.15 mmol L⁻¹ after 50 chambers filled with large colonies in each row. Usually many chambers are not filled with colonies, so that these numbers are unlikely to be reached in experiments.

Fig. 8 shows the percentage of the pure growth medium concentration remaining over the number of chambers filled with large colonies which operate at maximum uptake rates. While the lowest initial glucose concentration and the high PCA concentration can be expected to remain close to their initial value over the length of a chip, this is apparently not true for the lower initial PCA concentration and is currently under experimental validation.

Fig. 8 Remaining substrate concentrations in the supply channels depending on the number of chambers filled with large colonies with high uptake rates for different medium concentrations.

References

1. A. Grünberger, W. Wiechert and D. Kohlheyer, Curr. Opin. Biotechnol., 2014, 29, 15–23.
2. G. S. Fiorini and D. T. Chiu, BioTechniques, 2005, 38, 429–446.
3. X. Shi, W. Gao, J. Wang, S.-H. Chao, W. Zhang and D. R. Meldrum, Crit. Rev. Biotechnol., 2014, 1–13.
4. D. B. Weibel, W. R. DiLuzio and G. M. Whitesides, Nat. Rev. Microbiol., 2007, 5, 209–218.
5. A. Zanzotto, N. Szita, P. Boccazzi, P. Lessard, A. J. Sinskey and K. F. Jensen, Biotechnol. Bioeng., 2004, 87, 243–254.
6. P. Sun, Y. Liu, J. Sha, Z. Zhang, Q. Tu, P. Chen and J. Wang, Biosens. Bioelectron., 2011, 26, 1993–1999.
7. H. Kortmann, P. Chasanis, L. M. Blank, J. Franzke, E. Y. Kenig and A. Schmid, Lab Chip, 2009, 9, 576–585.
8. P. Wang, L. Robert, J. Pelletier, W. L. Dang, F. Taddei, A. Wright and S. Jun, Curr. Biol., 2010, 20, 1099–1103.
9. W. Mather, O. Mondragón-Palomino, T. Danino, J. Hasty and L. S. Tsimring, Phys. Rev. Lett., 2010, 104, 208101.
10. D. J. Beebe, G. A. Mensing and G. M. Walker, Annu. Rev. Biomed. Eng., 2002, 4, 261–286.
11. C. Probst, A. Grünberger, W. Wiechert and D. Kohlheyer, J. Microbiol. Methods, 2013, 95, 470–476.
12. C. Probst, A. Grünberger, N. Braun, S. Helfrich, K. Nöh, W. Wiechert and D. Kohlheyer, Anal. Methods, 2015, 7, 91–98.
13. S. Unthan, A. Grünberger, J. van Ooyen, J. Gätgens, J. Heinrich, N. Paczia, W. Wiechert, D. Kohlheyer and S. Noack, Biotechnol. Bioeng., 2014, 111, 359–371.
14. N. Mustafi, A. Grünberger, R. Mahr, S. Helfrich, K. Nöh, B. Blombach, D. Kohlheyer and J. Frunzke, PLoS One, 2014, 9, e85731.
15. D. Binder, A. Grünberger, A. Loeschcke, C. Probst, C. Bier, J. Pietruszka, W. Wiechert, D. Kohlheyer, K.-E. Jaeger and T. Drepper, Integr. Biol., 2014, 6, 755–765.
16. C. Dusny, A. Grünberger, C. Probst, W. Wiechert, D. Kohlheyer and A. Schmid, Lab Chip, 2015, 15, 1822–1834.
17. A. Grünberger, N. Paczia, C. Probst, G. Schendzielorz, L. Eggeling, S. Noack, W. Wiechert and D. Kohlheyer, Lab Chip, 2012, 12, 2060–2068.
18. J. P. Brody, P. Yager, R. E. Goldstein and R. H. Austin, Biophys. J., 1996, 71, 3430–3441.
19. S. Helfrich, C. E. Azzouzi, C. Probst, J. Seiffarth, A. Grünberger, W. Wiechert, D. Kohlheyer and K. Nöh, Bioinformatics, 2015 DOI:10.1093/bioinformatics/btv468.
20. W. S. Low, N. A. Kadri and W. A. B. B. Wan Abas, Sci. World J., 2014, 2014, 1–11.
21. M.-C. Kim and C. Klapperich, Lab Chip, 2010, 10, 2464–2471.
22. F. S. Fritzsch, K. Rosenthal, A. Kampert, S. Howitz, C. Dusny, L. M. Blank and A. Schmid, Lab Chip, 2013, 13, 397–408.
23. W. Deen, Analysis of Transport Phenomena, OUP USA, 1998.
24. J. F. Comesaña, J. J. Otero, E. García and A. Correa, J. Chem. Eng. Data, 2003, 48, 362–366.
25. L. Bocquet and J.-L. Barrat, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 3079–3092.
26. N. S. Khan, I. M. Mishra, R. Singh and B. Prasad, Biochem. Eng. J., 2005, 25, 173–178.
27. J. K. Gladden and M. Dole, J. Am. Chem. Soc., 1953, 75, 3900–3904.
28. A. C. Ribeiro, V. M. Lobo, D. G. Leaist, J. J. Natividade, L. P. Veríssimo, M. C. Barros and A. M. Cabral, J. Solution Chem., 2005, 34, 1009–1016.
29. K. Srinivas, J. W. King, L. R. Howard and J. K. Monrad, Fluid Phase Equilib., 2011, 301, 234–243.
30. J. Villadsen, J. Nielsen and G. Lidén, Bioreaction Engineering Principles, Springer, 2011.
31. J. Monod, Annu. Rev. Microbiol., 1949, 3, 371–394.
32. V. F. Wendisch, A. A. de Graaf, H. Sahm and B. J. Eikmanns, J. Bacteriol., 2000, 182, 3088–3096.
33. A. Marx, A. A. de Graaf, W. Wiechert, L. Eggeling and H. Sahm, Biotechnol. Bioeng., 1996, 49, 111–129.
34. H.-W. Lee, J.-G. Pan and J.-M. Lebeault, Appl. Microbiol. Biotechnol., 1998, 49, 9–15.
35. S. Norland, M. Heldal and O. Tumyr, Microb. Ecol., 1987, 13, 95–101.
36. D. M. Mahlmann, J. Jahnke and P. Loosen, Eur. J. Phycol., 2008, 43, 355–364.
37. S. Okino, M. Suda, K. Fujikura, M. Inui and H. Yukawa, Appl. Microbiol. Biotechnol., 2008, 78, 449–454.
38. A. Grünberger, J. van Ooyen, N. Paczia, P. Rohe, G. Schiendzielorz, L. Eggeling, W. Wiechert, D. Kohlheyer and S. Noack, Biotechnol. Bioeng., 2013, 110, 220–228.
39. A. Grünberger, C. Probst, S. Helfrich, A. Nanda, B. Stute, W. Wiechert, E. von Lieres, K. Nöh, J. Frunzke and D. Kohlheyer, Cytometry, Part A DOI:10.1002/cyto.a.22779 , accepted.

---

Footnote

† These authors contributed equally to this work.

---