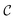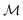Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Frequency modulated microrheology†
Matthew M.
Shindel
and
Eric M.
Furst
*
University of Delaware, Chemical and Biomolecular Engineering, Center for Molecular and Engineering Thermodynamics, 150 Academy St., Newark, Delaware, USA. E-mail: furst@udel.edu; Tel: +1 302 831 0102
First published on 21st April 2015
Abstract
Coupling analog frequency modulation (FM) to the driving stimulus in active microrheology measurements conducted with optical tweezers effectively parallelizes numerous single-frequency experiments. Consequently, frequency modulated microrheology (FMMR) can efficiently characterize the dynamic stress response of complex fluids over several frequency decades in a single experiment. The time required to complete an FMMR measurement scales with the lowest frequency probed, improving throughput over the serial frequency sweep approach. The ease of implementation, straight-forward data analysis and rapidity of FMMR offer particular utility toward applications such as characterization of non-equilibrium materials, automated microrheology instrumentation, high-throughput screening of biomaterials and (bio) pharmaceutical formulations, and in situ monitoring of chemical and biochemical reaction processes.
Introduction
Microrheology encompasses a suite of characterization tools that evaluate the stress response of complex fluids through analysis of the motion of embedded microscopic particles.1 Compared with traditional bulk techniques, the functional and practical advantages offered by microscopic forms of rheometry include small sample volumes (~1–50 μl), wide dynamic response (100−106 Hz), the capacity for local, global, and interfacial measurements, and the ability to incorporate the measurement into microfluidic devices.2 Microrheology is highly amenable to numerous applications in emerging areas of bio- and nanotechnology, particularly in instances where the materials of interest are scarce or difficult to obtain.3–7 Consequently, the development of microrheology methods that are increasingly easy to perform or serve as the operational kernel for automated instrumentation, will significantly benefit a variety of industries, as well as areas of active research and development, such as pharmaceuticals, polymer materials, and consumer care products.Microrheology measurements can be either passive or active. Passive microrheology relies on the diffusive motion of Brownian probes. Linear viscoelastic properties are extracted from the ensemble-averaged mean-square-displacement (MSD) of a probe population or from the MSD of a single probe confined by a localized potential field.8,9 The frequency range evaluated in a single measurement is bounded above by the bandwidth of the particle tracking method, and below by and total observation time. A material's constitutive stress response can also be determined by actively driving a colloidal probe within the host material via an external stimulus (active microrheology), commonly comprised by an optical or magnetic force.10–16 Similar to bulk rheometry, frequency sweeps (FS) are commonly used in active microrheology to discern storage and loss moduli piecewise, through consecutive application of an oscillatory driving force (mechanical, optical, electrokinetic, magnetic or otherwise). The oscillation frequency is sequentially stepped between discrete values in order to probe viscoelasticity over the desired spectral range.17–19 Although effective, sweeps are relatively laborious and become more time-consuming with increasing frequency resolution.
Alternatively, non-oscillatory approaches to microrheology have been devised with optical tweezers to provide broadband rheological characterization. Stochastic optical active rheology (SOAR) uses Gaussian noise to randomly displace an optical trap, extracting local viscoelastic properties from the psuedo-thermal motion of the probe.20 Wideband microrheology, formulated by Preece et al., examines the probe's step-response to discern the complex modulus of the surrounding environment.21
Frequency modulation (FM), the processes of encoding a signal via instantaneous frequency variations of a carrier wave, provides an additional route toward high-throughput active microrheology. Frequency modulated microrheology (FMMR) uses FM signal processing to construct a multi-modal, oscillatory driving force, with constant amplitude and frequency components that span the spectral range of interest. The majority of the input signal's energy is discretely accumulated in select harmonics, enabling parallelized evaluation of the host material's rheology (Fig. 1). The equivalent FM bulk rheology method, termed “multiwave rheology” or Fourier-transform mechanical spectroscopy has been particularly useful for capturing the evolution of gelators and other materials with time-dependent rheology.22,23
 | ||
| Fig. 1 Illustration of the frequency sweep (FS) and frequency modulation (FM) methods of active microrheology. | ||
Frequency modulation has a well-developed analytical framework due to its prominence in fields such as telecommunications, radar and telemetry, enabling straight-forward analysis of measurement data. This breadth in usage has also spawned an abundance of hardware and software utilities for synthesizing FM signals. Consequently, the resources required to implement FMMR are easily integrated with active microrheology instrumentation, including optical and magnetic tweezers.
This work provides an overview of the theory, experimental implementation and Fourier-based data analysis for FMMR. The technique is empirically validated in model Newtonian and viscoelastic fluids using optical tweezers. Measurement results from a recombinant human collagen solution are also presented. Finally, simulations in a generalized Maxwell fluid are used to compare settling times for FM and FS measurements.
Methods
Sample preparation
FMMR measurements were performed in Milli-Q filtered water and a 5% w/w aqueous solution of 200 kDa poly(ethylene oxide) (PEO; Sigma) containing 1.6 μm diameter polystyrene microparticles (ϕ < 10−4; Invitrogen). Samples were prepared in cells consisting of a glass coverslip (no. 1.5) and microscope slide joined with double-sided tape, and sealed with UV curable glue after loading, as described previously.24Optical tweezer microrheology
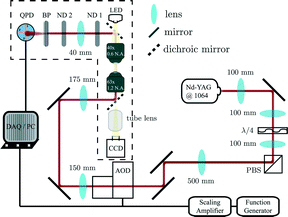
Microrheological measurements were performed using a laser tweezer system (Fig. 2) described previously.24 Briefly, an optical trap is generated by focusing a Nd–YAG laser (λ = 1064 nm; Coherent) to a diffraction limited spot with a 63× water-immersion objective (N.A 1.2). The trap is steered with an orthogonal pair of acousto-optic deflectors (AOD; A&A Optoelectronic). The particle's displacement from the optical trap is tracked interferometrically by imaging the condenser's back-focal-plane onto a quadrant photodiode (QPD; First Sensor).25 Sequential Impulse Response (SIR) is used to calibrate trap stiffness and detector sensitivity for each measurement.24The FM drive signal is synthesized by a function generator (Agilent 33220A), and offset with a DC voltage added by a scaling amplifier (SRS). The relative position of the optical trap, X(t), is given by a frequency modulated sinusoid with amplitude A.
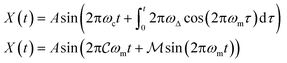 | (1) |
ω
c and ωm denote the carrier and modulation frequencies, respectively. The maximum instantaneous frequency deviation is given by ωΔ, while the ratio ωΔ/ωm defines the modulation index 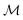 . Similarly, the carrier index is given by
. Similarly, the carrier index is given by 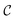 = ωc/ωm. Trap position and probe displacement were recorded with a data-acquisition card (National Instruments PCI-6221), at a rate of 40 kHz. All measurements were performed at T = 22 °C.
= ωc/ωm. Trap position and probe displacement were recorded with a data-acquisition card (National Instruments PCI-6221), at a rate of 40 kHz. All measurements were performed at T = 22 °C.
Data analysis
Neglecting inertial effects, the probe's dynamic behavior is modeled by a modified Langevin equation.| 0 = −∫t−∞R(t − τ)(ẇ(t) + Ẋ(t))dτ − κw(t) + FB(t) | (2) |
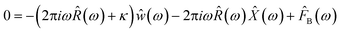 | (3) |
Applying the formalism of Mason and Weitz, the fluid's resistance is related to its complex viscosity ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) (ω) and particle radius (a) by the generalized Stokes equation,
(ω) and particle radius (a) by the generalized Stokes equation, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) (ω) = 6πa
(ω) = 6πa![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) (ω).8
(ω).8
Multiplying eqn (3) by the complex conjugate of trap position yields
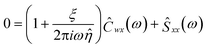 | (4) |
ξ denotes the characteristic optical stress, 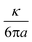 . The cross-power spectral density Ĉwx, and power spectral density Ŝxx, are the frequency-space representations of the cross- and auto-correlation functions, 〈ŵ
. The cross-power spectral density Ĉwx, and power spectral density Ŝxx, are the frequency-space representations of the cross- and auto-correlation functions, 〈ŵ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) *〉 and 〈
*〉 and 〈![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif)
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) *〉, respectively (brackets denote time-averaged quantities). The thermal force term is nullified because it is uncorrelated with trap position. The ratio −Ĉwx/Ŝxx defines the fluid's response function, Ĥ(ω). Substituting into 4 and rearranging gives a straight-forward expression for the fluid's complex modulus (Ĝ(ω) = 2πiω
*〉, respectively (brackets denote time-averaged quantities). The thermal force term is nullified because it is uncorrelated with trap position. The ratio −Ĉwx/Ŝxx defines the fluid's response function, Ĥ(ω). Substituting into 4 and rearranging gives a straight-forward expression for the fluid's complex modulus (Ĝ(ω) = 2πiω![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) ).
).
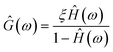 | (5) |
The FM input scans the band [ωc ± ωΔ] in an analog manner. However, the signal's power is stored at discrete frequencies, spaced by ωm, which have a one-to-one mapping onto the output for linear time-invariant systems. Filtering is required to sift out the activated spectrum. This can be done, for example, by thresholding the power spectral density of the drive signal, as shown in Fig. 3, or applying simple peak finding algorithms. Since the input signal has a known Fourier decomposition with coefficients given by a series of first-order Bessel functions, more sophisticated filtering procedures are feasible. However, simple filtering procedures are sufficient for the scope of this work.
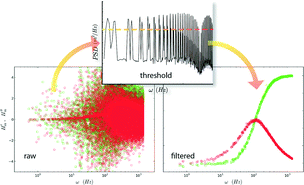 | ||
| Fig. 3 Filtering procedure for FMMR measurements. The power spectrum (middle) from the trap's positional signal is thresholded to to filter the raw response function. | ||
FMMR and other active techniques are effectively limited at high frequencies by the compliance of the optical trap. Probe displacement and trap position converge as the forcing frequency is increased. The disparity between these quantities ultimately falls below the resolution of the detector for ω ≫ ωk, where the trap corner frequency ωk = 2ξπ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) (0), prohibiting measurement of viscoelasticity. In light of this limitation, all maximum frequency of all FM inputs was limited to ~3 kHz, despite the fact that the Nyquist frequency was 20 kHz in all measurements.
(0), prohibiting measurement of viscoelasticity. In light of this limitation, all maximum frequency of all FM inputs was limited to ~3 kHz, despite the fact that the Nyquist frequency was 20 kHz in all measurements.
Results & discussion
Newtonian fluids
Newtonian fluids exhibit a purely dissipative stress response due to the properties of constant viscosity and zero elasticity. Under these conditions, resistivity is equivalent to the Stokes' drag coefficient, R = 6πηa. The response function for a Newtonian fluid is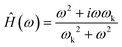 | (6) |
Measurements in water were performed with ωm = 0.7 Hz, 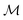 = 2142.1 and
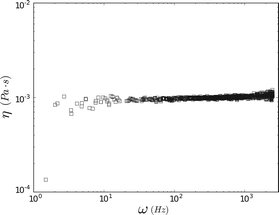
= 2142.1 and 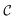 = 2142.9. The trap corner frequency, extracted from the calibration, was 110 Hz. The complex response function (Ĥ = H′ + iH′′) obtained via FMMR is in excellent agreement with eqn (6) (Fig. 4).
= 2142.9. The trap corner frequency, extracted from the calibration, was 110 Hz. The complex response function (Ĥ = H′ + iH′′) obtained via FMMR is in excellent agreement with eqn (6) (Fig. 4).
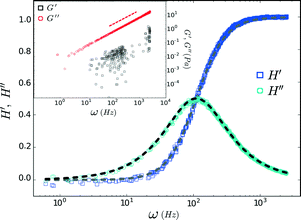 | ||
| Fig. 4 Response function measured in water. Dashed lines denote H′ (gray) and H′′ (black) from eqn (6) plotted with a corner frequency of 110 Hz. The inset shows the corresponding complex modulus and the dashed line represents the expected scaling for the loss modulus. | ||
The complex modulus obtained for water is shown in the inset of Fig. 4. The imaginary component, G′′, scales as ~ω, consistent with a Newtonian fluid. Similar to the ‘wideband microrheology’ method devised by Preece et al.,21 systematic and experimental noise sources give rise to elastic artifacts in Newtonian fluids. Drift and laser laser pointing instability can compromise the FMMR measurement at low frequency (≲10 Hz), where probe displacement is small. The positive G′ values clustered around 120 Hz arise due to AC electronic noise in the AOD power supply. Viscous drag increases with the speed at which the trap is rastered, causing the displacement amplitude registered by the detector to approach that of the drive signal. The disparity between the input and output amplitudes ultimately falls below the detector's resolution, limiting measurement accuracy at high frequency (ω ≫ ωk).
Dividing the loss modulus by 2πiω yields a constant viscosity (Fig. 5) of η = 1.00 ± 0.09 mPa s (mean ± standard deviation). These results are in excellent agreement with the known value (0.97 mPa s) for water at T = 22 °C, demonstrating the accuracy and efficacy of FMMR.
Viscoelastic materials
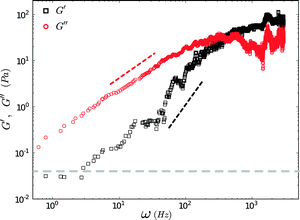
FMMR measurements in aqueous PEO (200 kDa) were performed with a polymer weight fraction of 5% w/w, an order-of-magnitude beyond the concentration threshold for viscoelastic behavior.The viscoelastic behavior of the polymer solution conforms to the single-mode Maxwell model (Fig. 6).26,32 The viscous modulus dominates below 500 Hz and displays an asymptotic scaling ~ω, while the storage modulus roughly scales as ~ω2 for frequencies in the range of 10–100 Hz.
The minimum shear modulus that can be determined from oscillatory measurements is constrained by the probe's thermal energy, kBT, and s, the spatial resolution of the QPD (ESI†).
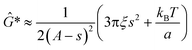 | (7) |
The instrument limitations described above, can potentially be circumvented by exploiting FMMR's capability to conduct high-resolution, wide-band scans. The Kramers–Kronig relation can be invoked to indirectly obtain G′ by integrating G′′.8,27
The applicability of FMMR to advanced, functional materials is demonstrated by measurements performed on recombinant type-III human collagen.28 The biopolymer is engineered with specific sites for intermolecular bonding through either direct coupling between macromolecules or bridging with a cross-linking reagent. This design enables the material's rheology to be optimized for various applications in tissue engineering and drug-delivery, using levers such as site density, ionic strength, pH and cross-linker valency and rigidity.29
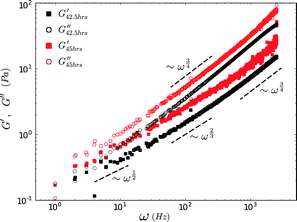
The rheology of a 1.2 mg ml−1 recombinant collagen solution was measured 42.5 and 45 hours after the addition of a multi-valent cross-linker using FMMR (Fig. 7). The biopolymer solution becomes increasingly viscoelastic over time, as indicated by the vertical shift in the shear modulus. Both storage and loss components exhibit fractional power-law growth with respect to frequency, consistent with theoretical descriptions of entangled polymer networks. Such scaling behavior in collagen gels and other biopolymer systems has been reported previously,13,27,30,31 and results obtained by FMMR are consistent with recently reported bulk rheology.29
The FMMR results are validated by data obtained during trap calibration. The SIR technique doubles as a non-oscillatory form of microrheometry.21,24 The shear modulus extracted from the probe's step-response overlaps with oscillatory measurements of the biopolymer's rheology (ESI†).
Frequency modulation versus frequency sweep
Measurement dynamics for the FM and FS schemes were evaluated through simulations in a Maxwell fluid, with complex viscosity32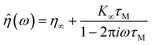 | (8) |
![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) to Ĝ and substituting into eqn (5). Brownian probe fluctuations were emulated by adding Gaussian noise to the output of each run. Fig. 8 illustrates how a simulated FM measurement converges over time.
to Ĝ and substituting into eqn (5). Brownian probe fluctuations were emulated by adding Gaussian noise to the output of each run. Fig. 8 illustrates how a simulated FM measurement converges over time.
Transient behavior in FMMR and sweep measurements were examined using the Allan variance of probe position.33 Originally developed to evaluate the stability of clocks and oscillators,34 this analysis can be used to optimize measurements subject to stochastic and systematic noise.35 Allan variance is defined as the average-square differential between the means of sequential subsets in a time-series.
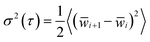 | (9) |
The number of data points, n, used to evaluate each local mean ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) i, determines the corresponding measurement lag-time,
i, determines the corresponding measurement lag-time, 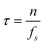 (ƒs is the measurement sampling frequency). The brackets 〈·〉 in eqn (9) denote an arithmetic average. The Allan deviation (σ(τ)) provides a measure of the statistical uncertainty in particle position, which directly dictates the accuracy of the rheological parameters discerned by microrheology. Because τ represents a block averaging time, the corresponding absolute time is a multiple of τ.
(ƒs is the measurement sampling frequency). The brackets 〈·〉 in eqn (9) denote an arithmetic average. The Allan deviation (σ(τ)) provides a measure of the statistical uncertainty in particle position, which directly dictates the accuracy of the rheological parameters discerned by microrheology. Because τ represents a block averaging time, the corresponding absolute time is a multiple of τ.
The probe's Brownian motion defines a lower bound for uncertainty in particle position (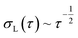 ). Oscillating the particle generates periodic perturbations from this thermal limit (Fig. 9), the amplitude (Δσ = σ − σL) of which decays as
). Oscillating the particle generates periodic perturbations from this thermal limit (Fig. 9), the amplitude (Δσ = σ − σL) of which decays as 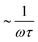 .33 The total time required for a piecewise sweep is simply the sum of all individual measurement periods.
.33 The total time required for a piecewise sweep is simply the sum of all individual measurement periods.
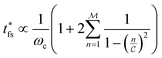 | (10) |
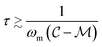 . Thus, t* for FMMR measurements is inversely proportional to the lowest active frequency (Fig. 10).
. Thus, t* for FMMR measurements is inversely proportional to the lowest active frequency (Fig. 10).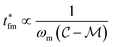 | (11) |
The ratio between t*fs and t*fm defines a relative efficiency metric, Γ
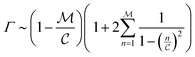 | (12) |
The summation 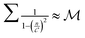 when
when 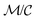 is small, leading to
is small, leading to 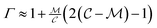 , which, as expected, reaches unity as
, which, as expected, reaches unity as 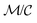 → 0. Fig. 11 shows Γ is non-monotonic but greater than unity for
→ 0. Fig. 11 shows Γ is non-monotonic but greater than unity for  ∈ (0, 1). The relative disparity in measurement speed can span several orders in magnitude, increasing with both resolution and bandwidth. Thus, FMMR is a more efficient approach to active microrheology.
∈ (0, 1). The relative disparity in measurement speed can span several orders in magnitude, increasing with both resolution and bandwidth. Thus, FMMR is a more efficient approach to active microrheology.
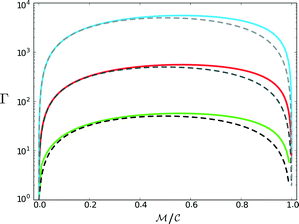 | ||
Fig. 11 Convergence time ratio between analogous frequency sweep and frequency modulation measurements. Solid lines denote numerically tabulated results from eqn (12) with  = 102 (green), 103 (red), and 104 (blue). Dashed lines show the analytical result when the summation is approximated as = 102 (green), 103 (red), and 104 (blue). Dashed lines show the analytical result when the summation is approximated as  . . | ||
Conclusions
FMMR parallelizes numerous single-mode measurements enabling rheological characterization over several frequency decades in a single pass. The technique operates with increased speed relative to the standard, linear sweep approach without compromising accuracy. FMMR provides tunable resolution and bandwidth, and is likely amenable to non-linear measurement because the active drive frequencies are known a priori.The rapidity and versatility of FMMR not only expands the applicable scope of active microrheology, but has notable industrial implications as well. The technique is simple to implement and can serve as the functional kernel for advanced microrheology instrumentation capable of highly automated operations and live display of a material's complex modulus. FMMR is particularly suited for materials that are difficult or costly to produce, and must be characterized over a broad parameter space. Emulating the μ2 rheology technique devised by Schultz and Furst,2 an FMMR-capable optical tweezer could be coupled with droplet microfluidics to create a system for high-throuput screening of biopharmaceutical, biomaterial and nanomaterial formulations.36 There is tremendous value inherent in such technology, since optimizing multi-variate formulations prior to scale-up can expedite commercialization, streamline manufacturing and curtail unanticipated cost overruns. Frequency modulation may have a number of non-rheological applications as well. AC and pulsed electric or magnetic fields instigate a variety of organizational and kinematic phenomena within colloidal dispersions, depending on particle size, shape and chemistry.37–39 The strength and frequency of the applied field govern the equilibrium microstructure and kinetic stability of non-equilibrium phases by regulating the intricate balance between thermodynamic interactions and particle mobility. FM may offer a tractable mechanism of control over self-assembly, transport and separation processes by providing a means of precisely sculpting a colloidal system's energy landscape.40 Encoding organization through a prescribed modulator signal is particularly intriguing,as it would facilitate scalable manufacturing of micro- and nano-structured materials with tailored physical, mechanical and thermal transport properties.
Acknowledgements
We thank Dr. S.-W. Wang and R. Que for providing recombinant collagen and acknowledge International Fragrances and Flavors for financial support of this project.References
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413 CrossRef.
- K. M. Schultz and E. M. Furst, Lab Chip, 2011, 11, 3802 RSC.
- T. Savin and P. S. Doyle, Soft Matter, 2007, 3, 1194 RSC.
- W. A. Petka, J. L. Harden, K. P. McGrath and D. Wirtz, Science, 1998, 281, 389 CrossRef CAS.
- W. Mulyasasmita, J. S. Lee and S. C. Heilshorn, Biomacromolecules, 2011, 12, 3406 CrossRef CAS PubMed.
- N. Yamaguchi, L. Zhang, B. S. Chae, C. S. Palla, E. M. Furst and K. L. Kiick, J. Am. Chem. Soc., 2007, 129, 3040 CrossRef CAS PubMed.
- C. Yan and D. J. Pochan, Chem. Soc. Rev., 2010, 39, 3528 RSC.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250 CrossRef CAS.
- M. Tassieri, R. M. L. Evans, R. L. Warren, N. J. Bailey and J. M. Cooper, New J. Phys., 2012, 14, 115032 CrossRef.
- M. T. Valentine and H. D. Ou-Yang, J. Phys.: Condens. Matter, 1996, 8, 9477–9482 CrossRef CAS.
- D. Velegol and F. Lanni, Biophys. J., 2001, 81, 1786–1792 CrossRef CAS.
- E. M. Furst, Curr. Opin. Colloid Interface Sci., 2005, 1, 79 CrossRef PubMed.
- T. A. Waigh, Rep. Prog. Phys., 2004, 68, 685 CrossRef.
- M. Tassieri, T. A. Waigh, J. Trinick, A. Aggeli and R. M. L. Evans, J. Rheol., 2010, 54, 117 CrossRef CAS.
- A. Yao, M. Tassieri, M. Padgett and J. Copper, Lab Chip, 2009, 9, 2568 RSC.
- L. G. Wilson and W. C. K. Poon, Phys. Chem. Chem. Phys., 2011, 13, 10617 RSC.
- I. Sriram, R. DePuit, T. M. Squires and E. M. Furst, J. Rheol., 2009, 53, 357 CrossRef CAS.
- F. Ziemann, J. Rädler and E. Sackmann, Biophys. J., 1994, 66, 2210 CrossRef CAS.
- L. A. Hough and H. D. Ou-Yang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031802 CrossRef CAS.
- H. Lee, Y. Shin, S. T. Kim, E. L. Reinherz and M. J. Lang, Appl. Phys. Lett., 2012, 101, 031902 CrossRef PubMed.
- D. Preece, R. Warren, R. M. L. Evans, G. M. Gibson, M. J. Padgett, J. M. Cooper and M. Tassieri, J. Mod. Opt., 2011, 13, 044022 CrossRef.
- E. E. Holly, S. K. Venkataraman, F. Chambon and H. H. Winter, J. Non–Newtonian Fluid Mech., 1988, 27, 17–26 CrossRef CAS.
- M. In and R. K. Prud'homme, Rheologica Acta., 1993, 32, 556–565 CrossRef CAS.
- M. M. Shindel, J. W. Swan and E. M. Furst, Rheol. Acta, 2013, 52, 455 CrossRef CAS.
- F. Gittes and C. Schmidt, Opt. Lett., 1998, 23, 7 CrossRef CAS.
- B. R. Dasgupta, S. Y. Tee, J. C. Crocker, B. J. Frisken and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 5, 051505 CrossRef.
- D. Mizuno, D. A. Head, F. C. MacKintosh and C. F. Schmidt, Macromolecules, 2008, 41, 7194 CrossRef CAS.
- S. W. P. Chan, S.-P. Hung, S. Raman, G. W. Hatfield, R. Lathrop, N. A. Da Silva and S.-W. Wang, Biomacromolecules, 2010, 11, 1460 CrossRef CAS PubMed.
- R. Que, A. Mohraz, N. A. Da Silva and S.-W. Wang, Biomacromolecules, 2014, 15, 35403549 CrossRef PubMed.
- M. Shayegan and N. R. Forde, PLoS One, 2013, 8, e70590 CAS.
- B. Schnurr, F. Gittes, F. C. MacKintosh and C. F. Schmidt, Macromolecules, 1997, 30, 7781 CrossRef CAS.
- M. Grimm, S. Jeney and T. Franosch, Soft Matter, 2011, 7, 2076 RSC.
- M. Andersson, F. Czerwinski and L. B. Oddershede, J. Opt., 2011, 13, 044020 CrossRef.
- D. W. Allan, Proc. IEEE, 1966, 54, 221 CrossRef.
- F. Czerwinski, A. C. Richardson and L. B. Oddershede, Opt. Express, 2009, 17, 13255 CrossRef CAS.
- K. M. Schultz, A. V. Bayles, A. D. Baldwin, K. L. Kiick and E. M. Furst, Biomacromolecules, 2011, 12, 4178 CrossRef CAS PubMed.
- J. M. McMullan and N. J. Wagner, Soft Matter, 2010, 6, 5443 RSC.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591 CrossRef CAS PubMed.
- J. W. Swan, P. A. Vasquez, P. A. Whitson, E. M. Fincke, K. Wakata, S. H. Magnus, F. De Winne, M. R. Barratt, J. H. Agui, R. D. Green, N. R. Hall, D. Y. Bohman, C. T. Bunnell, A. P. Gast and E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023 CrossRef CAS PubMed.
- S. Torquato, Soft Matter, 2009, 5, 1157 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/c5lc00351b |
| This journal is © The Royal Society of Chemistry 2015 |