Open Access Article
Open Access ArticleThermodynamics of force-dependent folding and unfolding of small protein and nucleic acid structures
Mingxi
Yao
a,
Hu
Chen
ab and
Jie
Yan
*acd
aMechanobiology Institute, National University of Singapore, Singapore 117411. E-mail: phyyj@nus.edu.sg
bDepartment of Physics, Xiamen University, Xiamen, Fujian, 361005 China
cDepartment of Physics, National University of Singapore, Singapore 117542
dCentre for Bioimaging Sciences, National University of Singapore, Singapore 117546
First published on 12th March 2015
Abstract
In this paper, we outline the theoretical framework for understanding the equilibrium force-dependent folding and unfolding transitions of protein domains and small nucleic acid structures, both having small rigid folded structures and highly flexible unfolded polymeric chain conformations. A complete statistical description of the state described by the probability function ρξ(n,x), is obtained, where n is an index denoting the structural state, and x is the extension of the molecule. ξ denotes an external constraint applied to the molecule, which is either a constant force or a harmonic spring attached to one end of the molecule. The extension probability distribution regardless of the structural state: 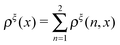 , the free energy landscape: −kBT
, the free energy landscape: −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρξ(x)), and the probability of the states regardless of the extension:
ln(ρξ(x)), and the probability of the states regardless of the extension: 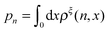 , are analyzed using the force-dependent structural transitions of the classic titin I27 domain as an example. The impact of different external constraints is also discussed.
, are analyzed using the force-dependent structural transitions of the classic titin I27 domain as an example. The impact of different external constraints is also discussed.
Insight, innovation, integrationSingle molecule manipulation techniques have been widely used to study the force induced structural transitions of biomolecules such as DNA and proteins. With recent advances in technology, increasing measurements are carried out under equilibrium conditions for a long time scale of several hours, in contrast to previous experiments carried out under non-equilibrium conditions over short experimental time scales of seconds to minutes. However, most of the current theoretical frameworks were originally developed to understand experiments carried out under non-equilibrium conditions with a focus on the kinetics of transitions. In this paper, we outlined a systematic theoretical framework to understand the force dependent unfolding and refolding of macromolecules under equilibrium conditions, which is linked to popular experimental systems such as magnetic tweezers, optical tweezers and AFM by introducing different external constraints into the molecules. We believe that such a theoretical description will be useful for both designing experiments and interpreting experimental results. |
Introduction
Single-molecular manipulation techniques have been widely used to study the force responses of macromolecules, such as DNA and proteins.1–3 Mechanical forces applied on macromolecules can drive transitions between different structural states, which depend on the differential entropic force responses of the respective structural states and the chemical energies that stabilize the folded state. Being a ubiquitous factor in cells, it is now broadly acknowledged that mechanical force is a key regulator of the functions of many biomolecules, influencing various important biological processes in development, tissue maintenance and diseases.4,5The force response of a biomolecule in a particular structural state and the force-dependent transitions between different structural states can be studied at the single-molecule level using single-molecule manipulation techniques. Currently, there are three major types of such techniques available, namely atomic force microscopy (AFM), optical tweezers and magnetic tweezers. They can mechanically stretch a single biomolecule by applying an external mechanical constraint to the molecule. In the cases of AFM and optical tweezers, it can be considered that the molecule is linked to an external harmonic spring at the end of the molecule, where the equilibrium position of the spring and the spring constant can be controlled. In the case of magnetic tweezers, constant forces are applied on the molecule using magnets through a paramagnetic bead attached to one end of the molecule.
In principle, the equilibrium properties of the force-dependent conformations and structural transitions can be obtained under a given external mechanical constraint by observing the extension fluctuation of the molecule. Such measurements require the maintenance of the external mechanical constraint (e.g., a constant force or a spring placed at a fixed position) for a long enough time to allow the molecule to sample all possible conformations and structures by thermal fluctuation. However, equilibrium fluctuations between different structures often involve overcoming high kinetic barriers and therefore have slow transition kinetics. Due to the rapid mechanical drift of the pulling devices, it has been challenging to study the force-dependent structural transitions under equilibrium conditions for many mechanically stable molecules. What has been typically done is forcing the molecule to unfold in a short time by rapidly moving the spring away from the molecule or by rapidly increasing the external force. Data obtained from such non-equilibrium measurements have been interpreted based on kinetic theories6–12 or non-equilibrium statistical mechanics.11
The most recently developed anti-drift technology, magnetic tweezers, has been reported to be able to maintain a constant force for several hours with negligible force drift and spatial drift.13 Such technical improvement has made it possible to probe the equilibrium mechanical folding and unfolding transitions of stable protein domains14–17 and small nucleic acid structures such as G-quadruplexes.18,19 However, a systematic theoretical framework based on equilibrium statistical physics dedicated to the understanding of the mechanical unfolding and folding of small protein domains and nucleic acid structures is still lacking. Motivated by the need for such a systematic theoretical framework for extracting information from equilibrium experimental measurements, we provide here a complete statistical description of the probability function ρξ(n,x), where n is an index denoting the structural state, x is the extension of the molecule, and ξ denotes an external constraint. We demonstrate the application of this probability function by analyzing the force-dependent structural transitions of the classic titin I27 domain, and discuss the impact of different external constraints on experimental observations.
The states of the system
To discuss the statistics of the force-dependent folding and unfolding problem, we describe the state of the system by (n,x) in this paper. Here n is the structural index, with n = 1 denoting the folded state, and n = 2 denoting the unfolded state. x is the extension of the molecule, which is the end-to-end distance vector of the molecule projected along the direction![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) .
.
The folded structure is typically a rigid body, which can be modeled as a rigid rod with a rod length of l0 in the absence of mechanical stretching. Its extension is simply x = l0![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ·
·![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . In the unfolded state, the molecule is typically an inextensible flexible polymer chain, with an extension of
. In the unfolded state, the molecule is typically an inextensible flexible polymer chain, with an extension of 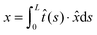 , where L is the polymer chain contour length.
, where L is the polymer chain contour length.
Force–extension curves of the respective structural states
When a molecule is stretched to an extension x, a tension f is built inside the molecule depending on the level of stretching. The relation f(x), or its inverse x(f), is referred to as the force–extension curve. The force–extension curve of a rod is simply the monomeric force–extension curve in the freely-jointed chain (FJC) polymer model, since each monomer in the FJC is treated as an independent rigid segment: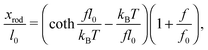 | (1) |
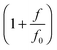 is added to allow a certain level of deformability of the rod,1 where f0 ≫ f to ensure a small deformability. Hereafter a rigid body described by eqn (1) is referred to as the extensible rigid body.
is added to allow a certain level of deformability of the rod,1 where f0 ≫ f to ensure a small deformability. Hereafter a rigid body described by eqn (1) is referred to as the extensible rigid body.
In the unfolded state, the conformation of the molecule can be described as an inextensible polymer chain with a weak bending rigidity. The force–extension curve of such polymers is described using the so-called worm-like chain model, which can be approximated analytically using the Marko–Siggia formula:20
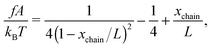 | (2) |
The above force–extension curves describe the entropic elasticity of the molecule in a particular structural state n. The resulting elastic energies at an extension x are:
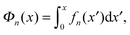 | (3) |
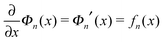 .
.
The conformational free energies under an external constraint
Under an external constraint ξ, the conformational free energy of the molecule in a particular state n includes a part from the entropic elastic energy of the molecule and another part from the external constraint, which can be generally described by the following equation: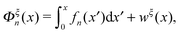 | (4) |
The derivative 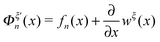 is the difference between the tension in the molecule and the force applied to the end from the external constraint, which is the mean force applied to the end of the molecule (mean force applied to the link point between the molecule and the constraint). At the equilibrium extension x = xeq,n, the mean force should be zero. Therefore, xeq,n can be solved from the equation Φξ′n(xeq,n) = 0. Considering Φξn(x) as a free energy landscape, xeq,n corresponds to the free energy minimum extension of the structural state n.
is the difference between the tension in the molecule and the force applied to the end from the external constraint, which is the mean force applied to the end of the molecule (mean force applied to the link point between the molecule and the constraint). At the equilibrium extension x = xeq,n, the mean force should be zero. Therefore, xeq,n can be solved from the equation Φξ′n(xeq,n) = 0. Considering Φξn(x) as a free energy landscape, xeq,n corresponds to the free energy minimum extension of the structural state n.
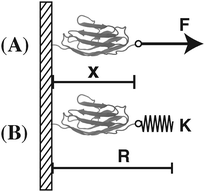
In this work, we focus our discussions on two commonly used constraints. One is the constraint of a constant external force of F applied to one end of the molecule, and the other is an external harmonic spring connected to one end of the molecule, which can be described by the equilibrium position of the spring and the spring constant (κ,R). The two different constraints are illustrated in the schematic shown in Fig. 1. wF(x) is the potential energy of the end of the molecule in the constant force field, while w(κ,R)(x) is the spring energy of the spring:
| wF(x) = −Fx, | (5a) |
| w(κ,R)(x) = ½κ(x − R)2. | (5b) |
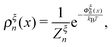 | (6) |
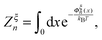 | (7) |
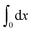 denotes the integral of the extension from zero to the allowed extension range of the molecule in the structural state n. In the subsequent discussions, the folded state is treated as an extensible rigid body, as such its extension can be longer than the contour length of the natively folded state l0. The unfolded state is treated as an inextensible WLC, and therefore its extension cannot exceed the contour length of the unfolded chain. Zξn only depends on the external constraint, from which the conformational free energy of the molecule in the structural state n can be calculated as: −kBT
denotes the integral of the extension from zero to the allowed extension range of the molecule in the structural state n. In the subsequent discussions, the folded state is treated as an extensible rigid body, as such its extension can be longer than the contour length of the natively folded state l0. The unfolded state is treated as an inextensible WLC, and therefore its extension cannot exceed the contour length of the unfolded chain. Zξn only depends on the external constraint, from which the conformational free energy of the molecule in the structural state n can be calculated as: −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zξn.
Zξn.
Boltzmann distribution of the two-state system under a constraint
A complete statistical description of the two-state system under a consraint ξ requires the knowledge of the joint probability function of ρξ(n,x). The energy of the state can be written as:| gξ(n,x) = δn,1(Φξn(x) − μ(x)) + δn,2Φξn(x), | (8) |
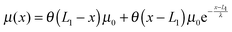 | (9) |
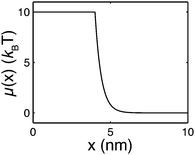 | ||
| Fig. 2 An example of the extension-dependent folding energy plotted at μ0 = 10 kBT, λ = 0.4 nm, and L1 = 4 nm. | ||
At equilibrium, ρξ(n,x) should follow the Boltzmann distribution:
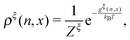 | (10) |
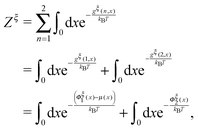 | (11) |
Gξtotal = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zξ. Zξ. | (12) |
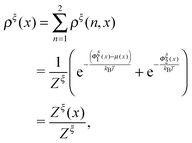 | (13) |
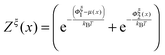 is a dimensionless quantity, which can be considered as a partition function under the external constraint ξ and an additional constraint of the extension x. Its ratio over the total partition function is therefore the probability density function of x.
is a dimensionless quantity, which can be considered as a partition function under the external constraint ξ and an additional constraint of the extension x. Its ratio over the total partition function is therefore the probability density function of x.
The so-called free energy landscape Gξ(x) defined as −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Zξ(x)) is shown as follows:
ln(Zξ(x)) is shown as follows:
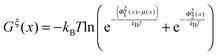 | (14) |
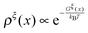 . Clearly, it determines the probability of the extension of the molecule under the constraint of ξ. The average and the variance of the extension can be calculated as:
. Clearly, it determines the probability of the extension of the molecule under the constraint of ξ. The average and the variance of the extension can be calculated as: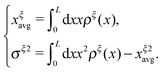 | (15) |
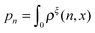 :
: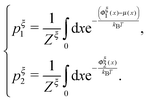 | (16) |
Applications
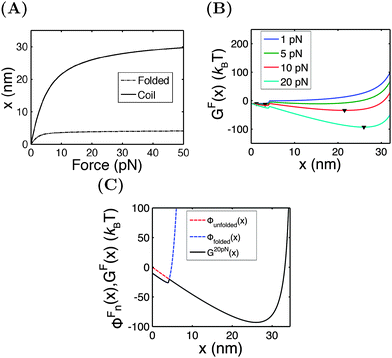
In this section, we demontrate the applications of the above theoretical framework by discussing the mechanical unfolding and folding transitions of the 27th immunoglobulin (Ig) domain of classic titin in the I-band (I27) as an example. This domain was studied extensively using AFM which revealed that I27 has an excellent mechanical stability to resist unfolding at >200 pN forces in the direct pulling mode3,21,22 and more recently using force-clamping AFM under a constant average force constraint through feedback control which revealed a much lower unfolding force (<100 pN).23 In the above studies, due to the mechanical drift of AFM, the measurements were not taken at equilibrium and therefore the measured unfolding force depended on the pulling speed in the direct pulling mode and the clamping time in the force-clamping mode. Most recently, the I27 domain was stretched using ultra-stable magnetic tweezers under a constant external force constraint which exhibited equilibrium unfolding and folding transitions at a very small force of ∼5 pN and a very low transition rate of ∼10−3 s−1. From this measurement, the equilibrium free energy difference between the folded and unfolded states was estimated to be ∼10 kBT.17 Here, we discuss the mechanical transitions of I27 under the constant force constraint and under a spring constraint based on the theoretical framework described in the preceding sections.An I27 domain has 89 amino acids (a.a.) and is folded into two β-sheets with seven β-strands. Treating it as a rigid rod with an l0 of ∼4 nm, its force–extension curve should follow eqn (1). A large value of f0 = 1000 pN is chosen to restrict its strain change within 10% under force <100 pN. After unfolding, it becomes a flexible peptide chain with a contour length of ∼33 nm and its force–extension curve follows the WLC model with a persistence length of A ∼ 0.8 nm,24 which can be described using the Marko–Siggia formula (eqn (2)).20Fig. 3A shows the force–extension curves of the folded and unfolded I27.
Under the constant force constraint described by eqn (5a), the free energy landscape is calculated based on eqn (14) and plotted in Fig. 3B for several different values of F. In the calculations, an extension-dependent folding energy described by eqn (9) with a native folding energy of μ0 = 10 kBT (ref. 17) and a decay constant of λ = 0.4 nm is used. The resulting free energy landscape GF(x) shows two energy minima which are separated by an energy barrier. The regions to the left and right of the energy barrier, which are a few kBT below the barrier, are dominated by the extension fluctuations of the folded and unfolded structures, respectively. This can be seen by plotting GF(x), ΦF1(x) − μ(x) and ΦF2(x) together (Fig. 3C). As a result, the energy minima of GF(x) are basically the equilibrium extensions of the folded state (n = 1) and the unfolded state (n = 2) determined by Φξ′n(xFn,eq) = 0. Due to the rigid body nature, xF1,eq has a weak force dependence and is close to the l0 at force 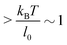 pN; however, due to the flexible chain elasticity of the unfolded peptide, xF2,eq has a strong force dependence and shifts to the right at increasing forces.
pN; however, due to the flexible chain elasticity of the unfolded peptide, xF2,eq has a strong force dependence and shifts to the right at increasing forces.
The energy barrier corresponds to the maximum located at 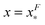 of GF(x). The “unfolding transition distance” can be defined as:
of GF(x). The “unfolding transition distance” can be defined as: 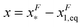 , which is very small and has a length scale close to λ. This is the general outcome of the unfolding of a rigid body which quickly loses its stability upon slight deformation. In contrast, the “folding transition distance” defined as
, which is very small and has a length scale close to λ. This is the general outcome of the unfolding of a rigid body which quickly loses its stability upon slight deformation. In contrast, the “folding transition distance” defined as 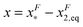 is dominated by the extension of the unfolded state and shows a strong dependence on force. Further, the “unfolding energy barrier” defined as
is dominated by the extension of the unfolded state and shows a strong dependence on force. Further, the “unfolding energy barrier” defined as 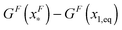 is dominated by the folding energy, which has a weak force dependence and is ∼μ0; while the “folding energy barrier” defined by
is dominated by the folding energy, which has a weak force dependence and is ∼μ0; while the “folding energy barrier” defined by 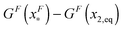 is dominated by the force response of the unfolded peptide chain with a strong force dependence. The critical force Fc at which the folded and unfolded states have equal probability is estimated by eqn (16) as Fc ∼ 5 pN.
is dominated by the force response of the unfolded peptide chain with a strong force dependence. The critical force Fc at which the folded and unfolded states have equal probability is estimated by eqn (16) as Fc ∼ 5 pN.
It should be noted that in such a two-state model, the physical meaning of the energy barrier is an extension state at which the mean force applied to the bead from the folded state is counter balanced by that from the unfolded state, weighted by their energies exponentially, 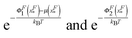 , respectively. It differs from the real “transition state” that corresponds to an ensemble of intermediate structural states. Furthermore, in such a two-state description of the unfolding and folding transitions, the transition rates purely depend on the bead diffusion in the free energy landscape, without taking into consideration the intrinsic time scale involved in the structural transitions that often dominates the rate of transitions. In spite of these limitations, the two-state model captures several generic features of the mechanical unfolding and folding transitions of rigid bodies, including a force-insensitive short unfolding transition distance, a force-sensitive folding transition distance, the relative probability of the folded and unfolded states under a given force constraint, etc.
, respectively. It differs from the real “transition state” that corresponds to an ensemble of intermediate structural states. Furthermore, in such a two-state description of the unfolding and folding transitions, the transition rates purely depend on the bead diffusion in the free energy landscape, without taking into consideration the intrinsic time scale involved in the structural transitions that often dominates the rate of transitions. In spite of these limitations, the two-state model captures several generic features of the mechanical unfolding and folding transitions of rigid bodies, including a force-insensitive short unfolding transition distance, a force-sensitive folding transition distance, the relative probability of the folded and unfolded states under a given force constraint, etc.
Fig. 4A shows the average (black, left axis) and the variance (red, right axis) of the extension as a function of force calculated by eqn (15). Increasing from 4 pN to 6 pN, the extension increases quickly from that of the folded state to that of the unfolded state. The variance shows a sharp rising profile during the transition with a peak located at Fc ± 1 pN, indicating a large extension fluctuation in this force range. Such a large extension fluctuation is caused by the equilibrium fluctuation between the two structural states. Fig. 4B shows the probabilities of the folded and unfolded states as a function of F calculated by eqn (16), indicating a switch from the folded state to the unfolded state when force is increased over a narrow range from 4 pN to 6 pN.
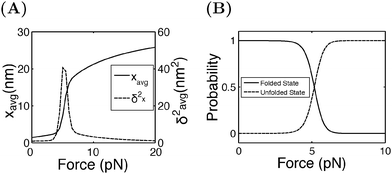 | ||
| Fig. 4 (A) The average and the variance of I27 under a constant force constraint of F. (B) The probabilities of the folded and unfolded states of I27 as a function of F. | ||
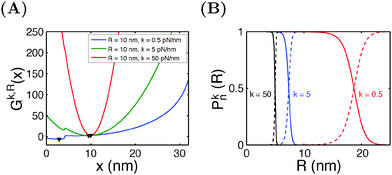
Similar calculations can be done for the spring constraint of a spring constant (κ,R). Fig. 5A shows the free energy landscape Gκ,R(x) obtained at R = 10 nm and different values of κ from 0.5 pN nm−1 to 50 pN nm−1. For κ = 0.5 pN nm−1, two energy minima are observed, with the folded state being more stable, as indicated by its lower level of energy compared to that of the unfolded state. At κ = 5 pN nm−1, two energy minima are still observed, but the folded state becomes less stable than the unfolded state. At κ = 50 pN nm−1, the spring completely dominates the fluctuation of the bead. The extension of the molecule is nearly stretched to the equilibrium position of the spring, and it is in an unfolded state since the extension is much greater than the contour length of the folded state. Fig. 5B shows the probabilities of structural states of the molecule as a function of the spring position (R) for three different values of κ. In general, it shows that, compared to a stiffer spring, a softer spring needs to move a longer distance to unfold the molecule, with a less steep transition profile.
In typical AFM or optical tweezer experiments, the trap/cantilever position is controlled. The extension of the molecule indicated by the bead/cantilever-tip position is measured, and the force is a readout based on the calibrated spring constant of the trap/cantilever stiffness. Fig. 6A shows the average extension of I27 as a function of R calculated by eqn (15) for three different values of κ. It shows that during unfolding, a larger extension jump can be observed under a softer spring constraint than under a stiffer spring constraint. Fig. 6B shows the force change during unfolding as a function of the average extension, revealing that a larger force drop under a stiffer spring constraint than under a softer spring constraint. Importantly, both the magnitude of the unfolding force and the overall force–extension profile show a significant dependence on the spring stiffness. These results indicate that when a molecule is stretched by a spring, both the molecule and the spring should be considered as a combined thermodynamic system. The interpretations of the observed force–extension relationship during transitions must be based on the context of the spring constant used in the experiments.
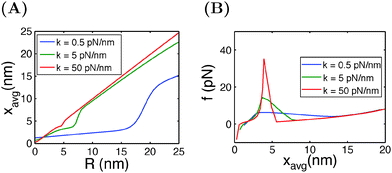 | ||
| Fig. 6 (A) Extension of I27 as a function of the spring position R, and (B) force as a function of the average extension, calculated at different spring constants κ. | ||
Summary and discussions
By describing the force–extension curve of the folded state as an extensible rigid rod and that of the unfolded state as a flexible chain, the joint probability function ρξ(n,x) has been derived for mechanical force-dependent two-state structural transitions of small protein domains and nucleic acid structures. The extension fluctuation ρξ(x) and the probability of the structural states pξn are derived as functions of the constraint, which can be directly related to experimental observations. Although we dedicated the discussions to the mechanical unfolding of small rigid-body structures, the theoretical framework is not limited to such structures. For a non-rigid body structure, one just needs to replace eqn (1) with the appropriate force–extension curve for the structure.Two commonly used external mechanical constraints are discussed: one is the constant force constraint typically implemented in magnetic tweezer experiments, and the other is the external spring constraint typically implemented in AFM/optical tweezer experiments. We have shown that different constraints lead to different experimental observations during the mechanical unfolding and folding of the molecules. In particular, in the case of the external spring constraint, interpretation of experimental data should consider the molecule and the spring as a combined thermodynamic system.
All equations are derived based on equilibrium statistics. In the derived free energy landscape, the difference in the free energies of the folded and unfolded states determines their relative probabilities under a constraint. The energy barrier in the free energy landscape is mainly contributed by the folding energy of the folded state, which does not provide a realistic description of the actual transition state that typically corresponds to an ensemble of intermediate structural states, which are different for different molecules. With a slight modification of the free energy landscape described in the paper, it is possible to describe the kinetics of real experiments more realistically, for example by changing the height of the energy barrier treating it as a free parameter to match the barrier height estimated in experiments.
Acknowledgements
The work in Singapore was funded by the Singapore Ministry of Education Academic Research Fund Tier 3 (MOE2012-T3-1-001) and Tier 2 (MOE2013-T2-1-154), and the National Research Foundation through the Mechanobiology Institute Singapore (to JY). The work in China was funded by the Fundamental Research Funds for the Central Universities (2013121005) and the National Nature Science Foundation of China (11474237) (to HC).References
- S. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795 CrossRef CAS
.
- M. Rief, M. Gautel, F. Oesterhelt, J. Fernandez and H. Gaub, Science, 1997, 276, 1109 CrossRef CAS
.
- M. Carrion-Vazquez, A. Oberhauser, S. Fowler, P. Marszalek, S. Broedel, J. Clarke and J. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3694 CrossRef CAS
.
- V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265 CrossRef CAS PubMed
.
- S. W. Moore, P. Roca-Cusachs and M. P. Sheetz, Dev. Cell, 2010, 19, 194 CrossRef CAS PubMed
.
- F. Ritort, C. Bustamante and I. Tinoco, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 13544 CrossRef CAS PubMed
.
- R. Berkovich, S. Garcia-Manyes, M. Urbakh, J. Klafter and J. M. Fernandez, Biophys. J., 2010, 98, 2692 CrossRef CAS PubMed
.
- R. Berkovich, S. Garcia-Manyes, J. Klafter, M. Urbakh and J. M. Fernandez, Biochem. Biophys. Res. Commun., 2010, 403, 133 CrossRef CAS PubMed
.
- R. Berkovich, R. I. Hermans, I. Popa, G. Stirnemann, S. Garcia-Manyes, B. J. Berne and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14416 CrossRef CAS PubMed
.
- M. Hinczewski, J. C. M. Gebhardt, M. Rief and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4500 CrossRef CAS PubMed
.
- N. C. Harris, Y. Song and C. H. Kiang, Phys. Rev. Lett., 2007, 99, 068101 CrossRef
.
- H. Lannon, J. S. Haghpanah, J. K. Montclare, E. Vanden-Eijnden and J. Brujic, Phys. Rev. Lett., 2013, 110, 128301 CrossRef CAS
.
- H. Chen, H. Fu, X. Zhu, P. Cong, F. Nakamura and J. Yan, Biophys. J., 2011, 100, 517 CrossRef CAS PubMed
.
- H. Chen, X. Zhu, P. Cong, M. P. Sheetz, F. Nakamura and J. Yan, Biophys. J., 2011, 101, 1231 CrossRef CAS PubMed
.
- M. Yao, B. T. Goult, H. Chen, P. Cong, M. P. Sheetz and J. Yan, Sci. Rep., 2014, 4, 4610 Search PubMed
.
- M. Yao, W. Qiu, R. Liu, A. K. Efremov, P. Cong, R. Seddiki, M. Payre, C. T. Lim, B. Ladoux, R. M. Mege and J. Yan, Nat. Commun., 2014, 5, 4525 CAS
.
- H. Chen, G. Yuan, R. S. Winardhi, M. Yao, I. Popa, J. M. Fernandez and J. Yan, J. Am. Chem. Soc., 2015, 137, 3540–3546 CrossRef CAS PubMed
.
- H. You, X. Zeng, Y. Xu, C. J. Lim, A. K. Efremov, A. T. Phan and J. Yan, Nucleic Acids Res., 2014, 42, 8789 CrossRef CAS PubMed
.
- H. You, J. Wu, F. Shao and J. Yan, J. Am. Chem. Soc., 2015, 137, 2424–2427 CrossRef CAS PubMed
.
- J. Marko and E. Siggia, Macromolecules, 1995, 28, 8759 CrossRef CAS
.
- P. E. Marszalek, H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten and J.
M. Fernandez, Nature, 1999, 402, 100 CrossRef CAS PubMed
.
- P. M. Williams, S. B. Fowler, R. B. Best, J. L. Toca-Herrera, K. A. Scott, A. Steward and J. Clarke, Nature, 2003, 422, 446 CrossRef CAS PubMed
.
- S. Garcia-Manyes, J. Brujic, C. L. Badilla and J. M. Fernandez, Biophys. J., 2007, 93, 2436 CrossRef CAS PubMed
.
- M. Rief, J. Pascual, M. Saraste and H. Gaub, J. Mol. Biol., 1999, 286, 553 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |