Cancer stem cells: small subpopulation or evolving fraction?

Abstract

Central to the debate about cancer stem cells in solid tumors is the proportion of cells that can initiate, propagate, and re-initiate tumors. An initially assumed minor subpopulation is confronted with recent data suggesting as many as 30% of primary tumor cells have stem cell characteristics. This review discusses quantitative modeling studies that augment our understanding of stem and non-stem cancer cell interactions during tumor progression and the resulting fraction of cancer stem cells. A discussion of how these findings can be carefully evaluated in novel, integrated interdisciplinary studies is offered.

---

Heiko Enderling

Heiko Enderling, PhD, is Assistant Member in the Integrated Mathematical Oncology department at Moffitt Cancer Center, where he directs a research group with focus on modeling stem cells, development and cancer. His exemplary interdisciplinary career began with an undergraduate degree in Computer Science applied to human medicine at the University of Magdeburg, Germany, followed by graduate studies in Mathematical Biology at the University of Dundee, Scotland. After a postdoctoral fellowship he advanced to the rank of Assistant Professor at the Center of Cancer Systems Biology at Tufts University School of Medicine. He moved to Moffitt Cancer Center in 2013.

---

Insight, innovation, integration

This review features a discussion of mathematical and computational models of tumor growth dynamics that directly or indirectly inform us about the fraction of cancer stem cells. It discusses cell–cell interactions as well as interaction of cancer cells with their microenvironment at different stages of tumor growth and during treatment. The article emphasizes the power of quantitative modeling in translating first-order principles into new hypotheses that motivate iterative, integrated theoretical-biological studies to settle the argument about cancer stem cell fraction size.

Introduction

After Till and McCulloch discovered stem cells at the top of the hematopoietic system hierarchy in the 1960s,¹ it became apparent that human acute myeloid leukemia is also organized hierarchically. Leukemia is initiated and fueled by a leukemic stem cell that gives rise to transit-amplifying progenitor cells and eventually differentiated cancer cells with limited lifespan.² The tumor stem cell terminology is attributed to Carney,³ who found the ‘stem cell nature’ of clonogenic lung cancer cells initiating tumors that mimicked lung cancer in nude mice.⁴ Retrospectively, the term ‘cancer stem cell’ probably caused a more heated debate than the subject itself. ‘Cancer stem cell’ may suggest the malignant transformation of a ‘tissue stem cell’, which due to its longevity and potency could serve as a cell of disease origin.^5–8 Although intestinal cancer may be initiated by a transformed stem cell,⁹ a mutated progenitor cell with acquired stem-like traits is more likely to initiate myeloid malignancies and NF1- and PDGF-driven glioblastoma.^10,11 In the colonic crypt, a stem cell or a transit-amplifying cell may become a cancer stem cell, dependent on which cell type first circumvents inhibitory feedbacks.^12,13 Further fueling the terminology debate is the variety of names for cancer stem cells, including tumor stem cells,¹⁴ tumorigenic cells,¹⁵ tumor-initiating cells,¹⁶ and tumorigenic side population,¹⁷ to name just a few. Even individual research groups change the terminology of their identified cell populations in subsequent publications, arguably due to journal and editorial staff preferences.

The first decade of the 21st century saw an advent of prospective identifications of cancer stem cells in various tissues including breast,¹⁸ brain,¹⁹ prostate,²⁰ and colon.^21,22 Cancer stem cells in most, if not all, organ systems are identified, or better enriched for, through the expression of surface markers. Surface marker expression may not be unique to cancer stem cells,²³ and putative stem cell marker expression in tumor populations spreads many orders of magnitude for most tumors, with even higher variations when experimental model systems vary.^24–26 Dilution assays on these subpopulations suggest that the actual fraction of true stem cells in already small, enriched subpopulations is less than 1%, prompting the widely held notion that cancer stem cells are a minor subpopulation. Although this is a seemingly trivial statement about proportions, much is put at stake. The concept of cancer stem cells in some tissues was challenged in its entirety by Sean Morrison, a co-author of the article that first identified breast cancer stem cells,¹⁸ who in 2008 showed that as many as 27% of unselected melanoma cells from different patients form tumors under permissive conditions.²⁷ This fueled the discussions about whether rare cancer stem cells are needed to drive tumor growth,²⁸ and whether a cancer stem cell population per se exists.²⁹ Kern and Shibata cautioned about the ‘fuzzy math’ often employed to explain subpopulation fractions in different experimental setups.³⁰

Although prospective identifications of cancer stem cells suggested the stem cell population to be small, its relative size was not an identifier. The predominant notion of minority, however, shatters the stem cell community due to its subjectivity. Is 27% a small subpopulation? If expressed mathematically—the unifying language of nature—subjectivity is put aside. Borrowing from set theory, the set of cancer stem cells is a true subset of cancer cells if at least one cancer cell is not a stem cell. It also remains a subset if all cells are cancer stem cells. Hence, any frequency of cancer stem cells is a subpopulation. Even a pure cancer stem cell population does not negate the cancer stem cell hypothesis, though this would mimic the more traditional view that most if not all cells in a tumor can proliferate extensively and metastasize successfully.³¹ The true hypothesis then is the existence of cancer cells that cannot form tumors and, pedantically, should be the cancer non-stem cell hypothesis.³²

Cancer (stem) cell kinetics

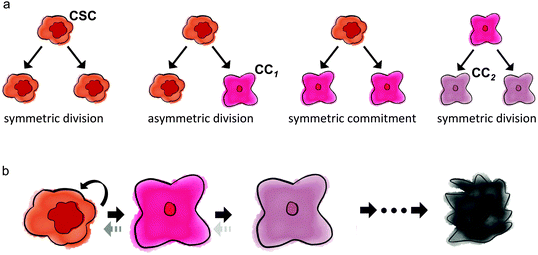
The fraction of cancer stem cells in a tumor emerges as a result of the interplay between stem and non-stem cancer cells, which depends on their respective underlying phenotypic kinetics. All cancer cells can undergo symmetric division, in that the fate of both daughter cells is identical to the fate of the mother cell. Cancer stem cells additionally have the ability to divide asymmetrically, whereby one daughter cell remains a stem cell, while the other daughter cell adopts a non-stem cancer cell trait. Fig. 1 summarizes the kinetics of stem and non-stem cancer cells. The probabilities of symmetric and asymmetric division are driven intrinsically by gene expression, but can also be modulated by external signals provided by the so-called niche.³³ Intracellular Wnt and Notch pathways have been shown to regulate the division fate of colon stem and colon cancer stem cells.³⁴ On the other hand, EGF/bFGF-rich environments regulate glioma stem cells to divide symmetrically more than 80% of the time. Growth factor withdrawal decreases symmetric division by 17% in favor of asymmetric division.³⁵

Fig. 1 Stem and non-stem cancer cell kinetics. (a) Cancer stem cells (CSC) can divide symmetrically and asymmetrically (which produces a first generation non-stem cancer cell (CC₁)), or undergo symmetric commitment, whereby both daughter cells adopt a CC₁ fate. Cancer cells of generation i divide symmetrically to generate two i + 1 generation daughter cells (CC₁ → 2 × CC₂). (b) Cancer cell fate lineage. Final-generation daughter cells with an exhausted ‘mitotic clock’ die in a subsequent mitosis attempt. Dotted arrows indicate potential de-differentiation and phenotypic plasticity.

For tumor initiation and re-initiation capability, the cancer stem cell population must be virtually inexhaustible. If cancer stem cells are mortal, self-renewal must occur at higher rates than cell death or differentiation. The inability of non-stem cancer cells to initiate tumors infers their limited proliferation potential. At each non-stem cancer cell division, both daughter cells inherit a decremented potency, arguably due to shortening of telomeres, the non-coding DNA repeats at the end of chromosomes.^36,37 Telomeric erosion inevitably leads to arrest, senescence, and cell death.^38,39 Upregulated telomerase rebuilds telomeric DNA,⁴⁰ and telomerase activity in cancer stem cells may be the key to longevity.^41,42 Telomere length may be surprisingly short in cancers, indicative of low non-stem cancer cell proliferation potential.⁴³

Cancer (stem) cell plasticity

In recent years, discussions have emerged that stemness may not be a cancer cell phenotype; rather it might be a transient state that can be induced and lost dependent on the cellular environment and signaling context.^44–47 Cells within the stemness niche adapt a stem cell state, and cells leaving the niche lose stem cell characterization. Acquisition of stem cell properties has been demonstrated through induced pluripotency,⁴⁸ which following the Waddington landscape can be described as a push from an energetically favorable differentiation state in a valley uphill beyond energetic barriers to a transient progenitor state.^49,50 Plasticity in cellular fate adds additional layers of complexity to the discussion about the proportion of cancer stem cells. First, the number of cancer stem cells then depends on both time and niche affinity. Second, it introduces heterogeneity within the stem cell population. Early progenitors that adapt a stem cell state confer different kinetic properties to the new stem cell than de-differentiating cells that are closer to their terminal phenotype. Quantitative mathematical and in silico agent-based computational models may help decipher the complexity that arises from the myriads of stem and non-stem cancer cell interactions. This review summarizes some of the most prominent mathematical and computational models and discusses their conclusions about the fraction of cancer stem cells in tumors.

Mathematical models elucidating cancer stem cell fractions

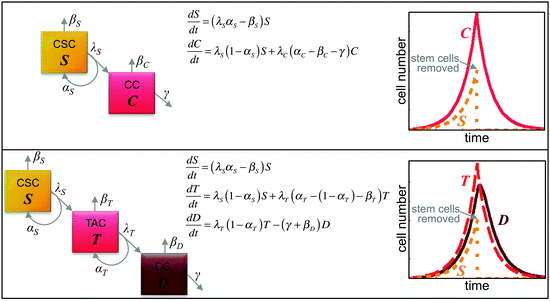
Enriching the discussion about the frequency of cancer stem cells in tumors is a rapidly growing number of quantitative mathematical models of stem cell-driven tumors. By reducing the complex biology of stem and non-stem cancer cell interactions into minimalistic and intentionally simplistic mathematical and computational models, first-order principles and key underlying biological mechanisms can be identified, from which long-term population evolution dynamics and causality conclusions may be drawn. Each tumor subpopulation can be described as a compartment, and compartments are connected by transition rates describing asymmetric division or (de)differentiation events. Let S(t) and C(t) respectively describe the number of cancer stem cells and non-stem cancer cells at time t. The number of cells changes over time, which may be described by differential equations dS/dt and dC/dt (difference in cell number, dS or dC, per difference in unit time, dt; dt = 1 day for example; Fig. 2). The proportion of cells that undergoes biological changes in the time window dt can be measured experimentally and translated into parameters in the mathematical equations.⁵¹ More sophisticated models may include additional subpopulations including transit-amplifying cells (i.e., T) and differentiated cells (i.e., D) (Fig. 2).

Fig. 2 Example of two- and three-compartment mathematical models. Graphical scheme of the models (left), mathematical formulation of the schematic model (center), and exemplary simulation result for tumor growth from initially one cancer stem cell (right). At half time, the stem cell population is removed to visualize population collapse without cancer stem cells. S: population of cancer stem cells (CSC), C: population of non-stem cancer cells (CC), T: population of transit-amplifying cells (TAC), D: population of terminally differentiated cells (DC). λ_* proliferation rates, α_* self-renewal probabilities, β_* death rates, and γ mitotic exhaustion rate.

Using a differential equation model, Johnston et al. showed that any fraction of cancer stem cells is possible, dependent on the balance of cancer stem cell self-renewal and differentiation rates.⁵² To sustain exponential tumor growth with a cancer stem cell population of less than 1% of the total tumor, symmetric and asymmetric cancer stem cell division rates must be of the same order of magnitude, and non-stem cancer cells must divide more frequently and have significantly higher cell death rates.⁵³ In addition to net growth rates of tumor subpopulations, the fraction of cancer stem cells in exponentially growing tumors also depends on the generational hierarchy of the non-stem cell population, which is determined by the non-stem proliferation potential, vis-à-vis telomere length.⁵⁴ Intuitively, the fraction of cancer stem cells is inversely related to the non-stem cell proliferation potential. Larger proliferation potentials give rise to larger non-stem populations, which decrease the proportion of cancer stem cells.

An analysis of the growth dynamics of multicellular spheroids in vitro with differential equations that include exponential growth and inter-conversion between stem and non-stem cancer cells suggests a transient cancer stem cell fraction that decreases from stem cells being a majority to a stable proportion of about 1.5%.⁵⁵ However, as tumors increase in volume, their growth becomes self-regulated.^56,57 To observe such growth saturation, negative feedback loops from non-stem cancer cells on cancer stem cell division, as well as on symmetric division rate, are required to control the cancer stem cell population.⁵⁸ Negative control has been confirmed to also maintain a constant cancer stem cell fraction under spatial considerations.⁵⁹ In addition to reciprocal feedback loops, the per capita rate of growth for all subpopulations depends on the tumor size in relation to its supporting tissue and organ structure. The consideration of a carrying capacity in logistic or Gompertzian growth models^60,61 exerts pressure on tumor subpopulations, enabling selection for and evolution of phenotypes with longevity. With a positive net growth rate of the cancer stem cell population combined with loss from the non-stem cell population when proliferation capacity is exhausted, the fraction of cancer stem cells monotonically increases.⁶² The time required to achieve a pure cancer stem cell population depends on the balance of kinetic parameters. However, such state likely exists only theoretically, as human life is short compared to evolutionary dynamics, and patients likely succumb to their primary and/or distant disease burden before the tumor is purified. Nevertheless, these studies suggest that the cancer stem cell fraction may not be an absolute value, but instead continuously evolving (Fig. 3).

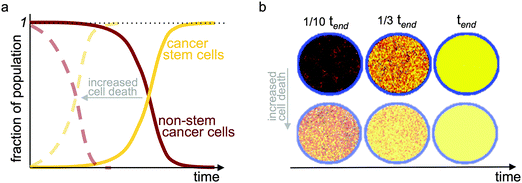Fig. 3 Evolution of temporal tumor subpopulations. Selection for cancer stem cells and evolution toward a pure cancer stem cell population (a) in a two-compartment mathematical model with a carrying capacity and cell turnover; and (b) in an agent-based model of stem and non-stem cancer cells in a confined circular domain (carrying capacity) and cell turnover. t_end refers to the simulation time when a pure stem cell population has evolved. Yellow: cancer stem cells; red-black: gradient of cell proliferation potential in non-stem cancer cells. Faded dashed curves in (a) and faded simulations in (b) show results with increased cell death providing faster turnover. Adapted from ref. 62.

Cell-based in silico models elucidating cancer stem cell fractions

Mathematical models of cancer stem cell-driven tumor growth have suggested that feedback loops between subpopulations as well as environmental selection pressures may play a pivotal role in determining the fraction of cancer stem cells. Spatially explicit cell-based computational models are uniquely positioned to simulate cell–cell and cell–environmental interactions and to investigate the roles of these interactions in modulating cancer stem cell fraction. Cells are individual agents with a set of intrinsic properties and rules to execute in response to environmental cues or when internal properties change (Fig. 4). Agent-based models are frequently utilized in theoretical oncology as single cell kinetics that are observed experimentally in vitro can be used to inform single cell behavior, and non-linear, complex and often unintuitive population level dynamics emerge without a priori constraints on the population. Assumptions about cell kinetics can be systematically challenged until population dynamics are observed that match experimental or clinical observations. Cell properties such as cell cycle phase times, migration rate, or proliferation fate can be fixed for simplicity or dynamically determined by internal and external signal processing. Dynamic cell properties can, for example, be modeled utilizing differential equations that determine subcellular protein concentrations or extracellular nutrient gradients. The behavior of each cell is individually advanced at discrete time steps, and complex population level dynamics emerge by many individual cells interacting with each other and competing for (or cooperating in) the same environment. The decision process of cell agents is conventually outlined in simulation flowcharts (Fig. 4). In agent-based models of cancer stem cell-driven tumors, the non-stem cancer cell population competes with stem cells for resources, including space in the simplest case. With low probability of symmetric cancer stem cell division, the non-stem population quickly outnumbers and encapsulates the founding stem cell, leading to spatial inhibition and tumor population dormancy.^63,64 The fraction of cancer stem cells – or single stem cells – then depends on the proliferation potential of progenitor non-stem cells, with larger proliferation potentials intuitively yielding a larger non-stem cancer population and thus a smaller stem cell ratio (Fig. 4) – analogous to the findings of the aforementioned multi-compartment mathematical model.⁵⁴ Liberation of the cancer stem cell may yield symmetric division and opportunistic spatial separation of the two stem cells to seed independent clones in each other's vicinity. The separation of individual tumor nodules increases the overall population's surface-to-volume ratio that enables decremented exponential growth.⁶⁵ This fractal morphology^66–68 yields self-similar nodules with a constant cancer stem cell fraction.⁶⁹ With increasing number of self-metastases, however, individual nodules may merge and saturate the local carrying capacity. Spontaneous or proliferation-limited non-stem cancer cell death transiently makes space available for which neighboring cells compete to proliferate into.⁷⁰ Such opportunistic proliferation selects for the long-lived stem cell population, which yields to a steady increase in cancer stem cell number in the population interior as well as increased overall stem cell fraction. Older tumors held at a local carrying capacity then harbor more stem cells than younger tumors.³²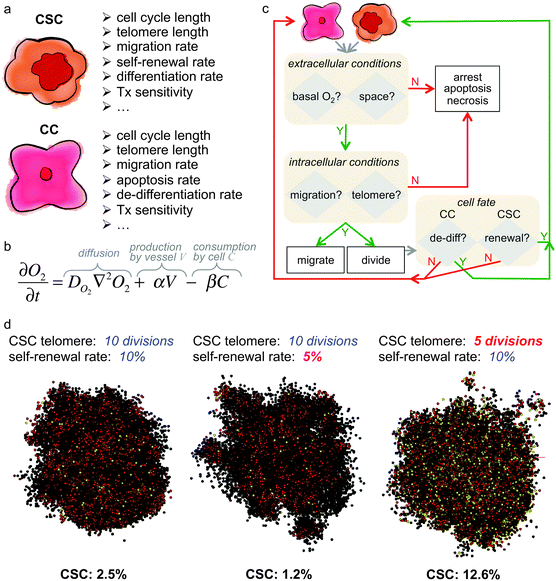

Fig. 4 Example of a hybrid in silico model of cancer stem cell-driven tumor growth. (a) Intrinsic properties of cancer stem cells (CSC) and non-stem cancer cells (CC). (b) Partial differential equation to model the concentration of oxygen (O₂). Adapted from ref. 104. (c) Example simulation flowchart for a hybrid in silico model. Adapted from ref. 62 and 104. (d) Sample simulations of cancer stem cell-driven tumor growth and cancer stem cell fraction dependent on cancer stem cell intrinsic properties. All tumors have 10 000 cells and were initiated with one CSC with properties as listed above each simulation snapshot. Color-coded are CSC in yellow, and red to black are CC with decreasing remaining telomere length. Adapted from ref. 62.

In silico cell-based models show that individual cell kinetics contribute to tumor growth and stem cell fraction in a non-monotonic manner; that is, while increasing a specific trait can promote tumor growth, a further increase in that trait may inhibit overall progression, and vice versa.^63,69 This yields to complex, nonlinear population-level dynamics with changes in every parameter, potentially modulating the cancer stem cell fraction and tumor morphology.^68,71 A tumor exclusively comprised of cancer stem cells – resembling the classic understanding of cancer that each cell is able to initiate, propagate and re-initiate a tumor – grows in a radially symmetric manner of a circle or a sphere, in two or three dimensions, respectively. Phenotypic cell heterogeneity yields irregular tumor growth with an invasive morphology at intermediate symmetric stem cell division rates and cancer stem cell fractions dependent on the balance of all cell kinetics contributing to tumor progression.^32,63,71

Treatment-modulated cancer stem cell fraction and kinetics

Compared to their non-stem counterparts, cancer stem cells are intrinsically more resistant to conventional cytotoxic therapies, including radiation^72,73 and chemotherapy^74,75 arguably due to a low proliferation rate combined with superior DNA repair mechanisms and molecular pumps that actively eject drugs from the cell.^72,76,77 With that, every application of therapy increases the fraction of cancer stem cells in a tumor⁷⁸ and treatment is only successful if all cancer stem cells are eradicated.⁷⁹ Therapy that leaves behind an enriched cancer stem cell population without significant non-stem cell competition can set up an aggressive repopulation.⁶³ Treatment-induced enrichment also varies greatly with dose rate.^80,81 Increased resistance to therapy alone, however, is insufficient to explain the dose rate-dependent enrichment in cancer stem cells; more complex dynamics must be at play. Treatment may transiently transition non-stem cancer cells into a stem cell state; mathematical and computational models have shown to match in vitro and in vivo experimental data in this regard.^81,82 Alternatively, treatment might create environmental conditions or promote intrinsic factors that trigger developmental survival and damage response programs in cancer stem cells that switch proliferation kinetics in favor of symmetric division.⁸³ Treatment-induced shifts in stem cell kinetics have also been observed in physiological settings. An integrated experimental-computational study of irradiating stem cells in the mammary gland showed that increased self-renewal and de-differentiation via epithelial–mesenchymal transition (EMT) are independent processes.⁸⁴ Stem and progenitor cell populations grow with increased self-renewal when combined with extensive proliferation such as during puberty, whereas EMT-modulated de-differentiation was shown to increase the stem cell fraction after irradiation in less proliferative adult glands.

Environmentally modulated cancer stem cell fractions

It is increasingly appreciated that stem cells may exist only in specific environments and their stemness maintained by factors in their niche.^85–89 Spindle-shaped N-cadherin+ CD45- osteoblastic cells that line the bone in the marrow form the niche of hematopoietic stem cells,⁹⁰ the subgranular zone of the hippocampal dentate gyrus and the subventricular zone of the lateral ventricle wall are neural stem cell niches,⁹¹ and paneth cells represent the niche for stem cells in intestinal crypts⁹² to name but a few. Abundance of EGF and bFGF has been shown to promote symmetric glioma stem cell division,³⁵ and Wnt in competition with Dickkopf1 regulates breast cancer stem cell fate.^93,94 In pathological tissues with loss of tissue architecture, cancer stem cells may be located in the bulk tumor but also prominently in the invasive tumor border zone.⁹⁵ This prevalence of cancer stem cells at the edge of the tumor combined with evidence of cell dissemination suggests that an epithelial–mesenchymal transition may induce stemness.^96,97 Plasticity in cell fate may be further fueled by spatial and temporal heterogeneity of the pathological environment. It is conceivable that inherently opposing perivascular and perinecrotic niches for cancer stem cells⁹⁸ are in fact the same geographic location within a tumor at different time points, with blood vessels occluding and reopening with varying tumor mass pressure.⁹⁹ Cancer stem cells adapt to nutrient restriction in perinecrotic areas by metabolic shifts to preferential glucose uptake,¹⁰⁰ and acidic environments may further promote survival and stem cell self-renewal through expression of angiogenic factors.¹⁰¹

Quantitative models of microenvironmental regulation of cancer stemness have been sparse. Sottoriva and colleagues were the first to make progress into in silico modeling of niche-directed stem cell kinetics.¹⁰² In a cellular automaton model, solid tumors with intrinsic stem cell renewal rates are compared to tumors whose stem cell division kinetics or stem cell state is determined by an arbitrary environment. Interestingly, intrinsic and environmental regulation of stem cell division yields comparable growth, morphologic instability, and phenotypic heterogeneity when environmental feedback is calibrated to yield cancer stem cell ratios similar to intrinsic kinetics. Characteristics of tumors with a cellular hierarchy are therefore quite robust, independent of what regulates the kinetics of the driving cell subpopulation.¹⁰²

Scott and colleagues adapted a hybrid discrete continuous framework¹⁰³ of individual in silico cells on a discrete layer and heterogeneous oxygen concentration that is modeled using partial differential equations on a continuous level.¹⁰⁴ Oxygen is produced at fixed locations of blood vessels arbitrarily distributed throughout the computational domain. Diffusion from areas of high oxygen concentration replenishes oxygen that is locally consumed by cancer cells, and cells die if basal oxygen falls below a sustainable level. Model simulations revealed that the combination of plausible symmetric stem cell renewal rates and progenitor proliferation capacities could yield different population dynamics. Populations are unsustainable if tumor cell density increases local oxygen tension that induces stem cell death. Population homeostasis, or tumor dormancy, is observed when the non-stem cell population spatially inhibits cancer stem cells without depleting oxygen. Homeostasis is disrupted and malignant population growth is observed in different vascular densities when progenitors are short-lived and oxygen is plentiful. Emerging local oxygen tension during aggressive growth yields local cell death and subsequent repopulation by adjacent cell colonies.¹⁰⁴ To adequately simulate the perturbation of self-renewal rates by stem cell niche factors, direct feedback on cell kinetics must be modeled. Gentry and Jackson incorporated niche feedback on cell kinetics in a differential equation framework of stem cell homeostasis and mutation-derived perturbation to exponential malignant growth.¹⁰⁵ Stem cells secrete chemical factors that inhibit self-renewal and avoid overcrowding of the niche. A small stem cell population yields a low inhibitory factor concentration that increases stem cell symmetric division. Mutations may cause stem cells to become independent of environmental feedback. A continued proliferation of mutated stem cells increases cell density in the niche and forces unmutated stem cells into differentiation. In combination with increasing the carrying capacity of stem cells, cancer stem cells quickly develop if their mutation trajectory follows decreased cell death, faster proliferation with higher self-renewal rates, and increased mutation rates.¹⁰⁵

In an integrated computational-experimental study, Agur and Clarke developed a model of cell interaction kinetics dependent on intra- and inter-cellular concentrations of breast cancer stem cell-regulating proteins, including Dickkopf1 (Dkk1), Wnt, Notch, and E-cadherin.⁹³ Stem cells process external signals to determine internal protein levels that trigger cell proliferation or differentiation. The model predicts that increasing E-cadherin, Wnt, and Notch by 20% doubles the average cancer stem cell number in a fixed-size population and thus the cancer stem cell ratio. Continuous administration of high levels of Dkk1, a negative regulator of Wnt, is required to drive the cancer stem cell pool to extinction.⁹³ A continuous mathematical model of spatiotemporally varying stem cell-released feedback signals on stem cell division kinetics enables evaluation of tumor morphology evolution.⁵⁹ An initial cluster of cancer stem cells separates into individual stem cell pools near the boundary of the growing population that eventually break away into individual clusters. Each cluster is driven by a cancer stem cell or a small cancer stem cell population that is surrounded by non-stem cancer cells reminiscent of a self-metastatic morphology⁶⁸ that increases the surface-to-volume ratio⁶⁵ to prevent self-inhibition.^56,57

Discussion and future directions

The prospective identification of tumor-initiating cells has revolutionized our understanding of tumor biology and polarized the cancer research community.^29,106–109 If tumors were fueled by a small subpopulation of stem cells, then targeting theses cells – however difficult this might be – would provide a new therapeutic approach in lieu of gross tumor volume reduction with severe side effects to normal adjacent and distant tissues. Central to the cancer stem cell debate is the very fraction of the stem cell subpopulation. Although initial reports indicated a minor side population, a much larger fraction of cells with tumor-initiation capability has more recently been argued.²⁷ Further complicating matters are the use of different experimental protocols and endpoints to identify cancer stem cells and the eccentric use of mathematical calculations to derive stem cell fractions.³⁰ Quantitative scientists – mathematicians, computer scientists, physicists, and engineers – have taken notice of the fascinating field of cancer stem cells as well as the arising debates and controversies. Numerous theoretical studies of stem and cancer stem cells have been developed to investigate subcellular-, cellular-, and population-level biological dynamics using discrete, continuous, or hybrid modeling techniques.^110–128 Quantitative and qualitative models have provided novel, thought-provoking insights into the concept of cancer stem cell fraction. To identify the ratio of stem and non-stem cancer cells, one has to discriminate the conditions of tumor growth and regulation of cell kinetics. During unrestricted tumor growth, the early phase of Gompertzian growth dynamics^60,129–131 when resources are plentiful, physical constraints negligible and self-inhibitory signals diffusive, the constant fraction of cancer stem cells is likely to be small, as determined by the balance of biologically plausible cell intrinsic kinetic rates. This growth phase is conceivable to be reminiscent of in vitro conditions, and the ratio of cancer stem cells observed in laboratory experiments may provide valuable information about intrinsic proliferation and self-renewal rates as well as progenitor proliferative potentials.^53,54

Clinically apparent tumors in patients rarely follow an exponential growth trajectory. Tumor growth decelerates as the surface-to-volume ratio of the tumor decreases, arguably due to increased intratumoral pressure, a limited supply of nutrients to the interior, and insufficient removal of metabolic waste products from the tumor core.^56,132–134 From the undisputed long-term self-renewal property of cancer stem cells and their superior survival mechanisms in harsh environments compared to their non-stem counterparts,¹⁰⁰ it follows that the tumor cell population becomes enriched in cancer stem cells over time. Therefore, the fraction of cancer stem cells in tumors that are forced into slow growth regimes or even dormancy is continuously evolving – a monotonic increase toward a pure cancer stem cell population.^32,62 The observed cancer stem cell fraction, although far from the theoretical equilibrium, may reflect the age of a tumor and its individual history in overcoming local carrying capacities.¹³⁵ Patients with comparable tumor subtype and pathology at diagnosis may have experienced vastly different tumor development trajectories, leading to different cancer stem cell fractions and opposing responses to treatment and overall survival, offering yet another motivation for personalized medicine.

Increasing the complexity of cancer stem cell biology is environmental modulation of intrinsic cell kinetics and phenotypic identity. Growth factors and inhibitory signals in the tumor microenvironment and cancer stem cell niche alter proliferation rate, self-renewal frequency, and even stemness character.^35,102,136 Continuous, reciprocal modulation of the tumor and its environment yields spatiotemporal heterogeneities in signaling factor prevalence, further suggesting a highly dynamic ratio of cancer stem cells. To fully understand stem cell and cancer stem cell behavior, experimental and theoretical modeling approaches must be integrated and iteratively inform and validate each other. The presented modeling studies suggest that experimental protocols should include sequential measurements to capture the temporal evolution of the cancer stem cell fraction in heterogeneous populations. Calibrated in silico simulations might help determine the experimental time points to keep increased experimental costs to a minimum. Furthermore, quantitative models have shown that the dynamics of complex systems are best understood if perturbed and far from equilibrium. Increased selection forces such as strengthened immune surveillance or cytotoxicity from therapeutic agents might provide such perturbations, with the added benefit to further our understanding of temporal responses of different phenotypes to clinical intervention.

While some of the herein discussed models are qualitative and others quantitative, they all are speculative. Each model is based on simple assumptions and subject to gross oversimplifications of reality to investigate confined questions. Nevertheless, quantitative models offer fascinating insights into the complex, nonlinear dynamics of a heterogeneous tumor population that mandate further conceptual, experimental, theoretical, and clinical investigations before taking sides in the discussion about stem cell prevalence. Regardless of whether model predictions will be experimentally confirmed or rejected, new biological insights will be derived that may inform the next generation of quantitative model development, hypothesis generation, and experimental verification.

Acknowledgements

This work was partially supported by the NIH/NCI Integrative Cancer Biology Program 5U54 CA113007. I would like to thank Arturo Araujo for help with Fig. 1 and David Basanta for critical reading of the manuscript.

References

1. A. J. Becker, E. A. McCulloch and J. E. Till, Nature, 1963, 197, 452–454.
2. D. Bonnet and J. E. Dick, Nat. Med., 1997, 3, 730–737.
3. D. N. Carney, A. F. Gazdar, P. A. Bunn and J. G. Guccion, Stem Cells, 1982, 1, 149–164.
4. E. H. Lin, Y. Jiang, Y. Deng, R. Lapsiwala, T. Lin and C. A. Blau, Gastrointest. Cancer Res., 2008, 2, 169–174.
5. R. A. Barker, M. Jain, R. J. E. Armstrong and M. A. Caldwell, J. Neurol., Neurosurg. Psychiatry, 2003, 74, 553–557.
6. G. Dontu, S. Liu and M. S. Wicha, Stem Cell Rev., 2005, 1, 207–213.
7. S. Fuchs and L. Sommer, Neurodegener. Dis., 2007, 4, 6–12.
8. K. Musunuru, I. J. Domian and K. R. Chien, Annu. Rev. Cell Dev. Biol., 2010, 26, 667–687.
9. N. Barker, R. A. Ridgway, J. H. van Es, M. van de Wetering, H. Begthel, M. van den Born, E. Danenberg, A. R. Clarke, O. J. Sansom and H. Clevers, Nature, 2009, 457, 608–611.
10. H. Haeno, R. L. Levine, D. G. Gilliland and F. Michor, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16616–16621.
11. D. Hambardzumyan, Y.-K. Cheng, H. Haeno, E. C. Holland and F. Michor, PLoS One, 2011, 6, e24454.
12. I. P. Tomlinson and W. F. Bodmer, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 11130–11134.
13. M. D. Johnston, C. M. Edwards, W. F. Bodmer, P. K. Maini and S. J. Chapman, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4008–4013.
14. R. Stupp and M. E. Hegi, Nat. Biotechnol., 2007, 25, 193–194.
15. J. Buchstaller, P. E. McKeever and S. J. Morrison, Cancer Cell, 2012, 21, 240–252.
16. S. K. Singh, C. Hawkins, I. D. Clarke, J. A. Squire, J. Bayani, T. Hide, R. M. Henkelman, M. D. Cusimano and P. B. Dirks, Nature, 2004, 432, 396–401.
17. B. Das, R. Tsuchida, D. Malkin, G. Koren, S. Baruchel and H. Yeger, Stem Cells, 2008, 26, 1818–1830.
18. M. Al-Hajj, M. S. Wicha, A. Benito-Hernandez, S. J. Morrison and M. F. Clarke, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3983–3988.
19. S. K. Singh, I. D. Clarke, M. Terasaki, V. E. Bonn, C. Hawkins, J. Squire and P. B. Dirks, Cancer Res., 2003, 63, 5821–5828.
20. A. T. Collins, P. A. Berry, C. Hyde, M. J. Stower and N. J. Maitland, Cancer Res., 2005, 65, 10946–10951.
21. C. A. O'Brien, A. Pollett, S. Gallinger and J. E. Dick, Nature, 2007, 445, 106–110.
22. L. Ricci-Vitiani, D. G. Lombardi, E. Pilozzi, M. Biffoni, M. Todaro, C. Peschle and R. De Maria, Nature, 2007, 445, 111–115.
23. J. M. Stewart, P. A. Shaw, C. Gedye, M. Q. Bernardini, B. G. Neel and L. E. Ailles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6468–6473.
24. J. E. Visvader and G. J. Lindeman, Nat. Rev. Cancer, 2008, 8, 755–768.
25. J. E. Visvader, Nature, 2011, 469, 314–322.
26. J. E. Visvader and G. J. Lindeman, Cell Stem Cell, 2012, 10, 717–728.
27. E. Quintana, M. Shackleton, M. S. Sabel, D. R. Fullen, T. M. Johnson and S. J. Morrison, Nature, 2008, 456, 593–598.
28. P. N. Kelly, A. Dakic, J. M. Adams, S. L. Nutt and A. Strasser, Science, 2007, 317, 337.
29. P. B. Gupta, C. L. Chaffer and R. A. Weinberg, Nat. Med., 2009, 15, 1010–1012.
30. S. E. Kern and D. Shibata, Cancer Res., 2007, 67, 8985–8988.
31. M. Shackleton, E. Quintana, E. R. Fearon and S. J. Morrison, Cell, 2009, 138, 822–829.
32. H. Enderling, L. R. Hlatky and P. Hahnfeldt, Front. Oncol., 2013, 3, 76.
33. L. I. Zon, Nature, 2008, 453, 306–313.
34. P. R. Prasetyanti, C. D. Zimberlin, M. Bots, L. Vermeulen, F. D. S. E. Melo and J. P. Medema, Mol. Cancer, 2013, 12, 126.
35. J. D. Lathia, M. Hitomi, J. Gallagher, S. P. Gadani, J. Adkins, A. Vasanji, L. Liu, C. E. Eyler, J. M. Heddleston, Q. Wu, S. Minhas, A. Soeda, D. J. Hoeppner, R. Ravin, R. D. G. McKay, R. E. McLendon, D. Corbeil, A. Chenn, A. B. Hjelmeland, D. M. Park and J. N. Rich, Cell Death Dis., 2011, 2, e200.
36. A. M. Olovnikov, J. Theor. Biol., 1973, 41, 181–190.
37. E. H. Blackburn and J. G. Gall, J. Mol. Biol., 1978, 120, 33–53.
38. J. Campisi, S. H. Kim, C. S. Lim and M. Rubio, Exp. Gerontol., 2001, 36, 1619–1637.
39. A. Preto, S. K. Singhrao, M. F. Haughton, D. Kipling, D. Wynford-Thomas and C. J. Jones, Oncogene, 2004, 23, 4136–4145.
40. C. W. Greider and E. H. Blackburn, Cell, 1985, 43, 405–413.
41. M. Armanios and C. W. Greider, Cold Spring Harbor Symp. Quant. Biol., 2005, 70, 205–208.
42. Z. Ju and K. L. Rudolph, Eur. J. Cancer, 2006, 42, 1197–1203.
43. J. W. Shay and W. E. Wright, Semin. Cancer Biol., 2011, 21, 349–353.
44. R. Poulsom, M. R. Alison, S. J. Forbes and N. A. Wright, J. Pathol., 2002, 197, 441–456.
45. A. J. Wagers and I. L. Weissman, Cell, 2004, 116, 639–648.
46. U. R. Rapp, F. Ceteci and R. Schreck, Cell Cycle, 2008, 7, 45–51.
47. L. Wang, B. L. Walker, S. Iannaccone, D. Bhatt, P. J. Kennedy and W. T. Tse, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6638–6643.
48. K. Takahashi and S. Yamanaka, Cell, 2006, 126, 663–676.
49. C. H. Waddington, The strategy of the genes, Allen & Unwin, 1957.
50. R. Morris, I. Sancho-Martinez, T. O. Sharpee and J. C. Izpisua Belmonte, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5076–5082.
51. H. Enderling and M. A. J. Chaplain, Curr. Pharm. Des., 2014, 20, 4934–4940.
52. M. D. Johnston, P. K. Maini, S. Jonathan Chapman, C. M. Edwards and W. F. Bodmer, J. Theor. Biol., 2010, 266, 708–711.
53. R. Molina-Peña and M. M. Álvarez, PLoS One, 2012, 7, e26233.
54. S. L. Weekes, B. Barker, S. Bober, K. Cisneros, J. Cline, A. Thompson, L. R. Hlatky, P. Hahnfeldt and H. Enderling, Bull. Math. Biol., 2014, 76, 1762–1782.
55. T. Peng, M. Qinghua, T. Zhenning, W. Kaifa and J. Jun, PLoS One, 2011, 6, e25518.
56. J. Folkman and M. Hochberg, J. Exp. Med., 1973, 138, 745–753.
57. R. T. Prehn, Cancer Res., 1991, 51, 2–4.
58. X. Liu, S. Johnson, S. Liu, D. Kanojia, W. Yue, U. P. Singh, U. Singn, Q. Wang, Q. Wang, Q. Nie and H. Chen, Sci. Rep., 2013, 3, 2473.
59. H. Youssefpour, X. Li, A. D. Lander and J. S. Lowengrub, J. Theor. Biol., 2012, 304, 39–59.
60. B. Gompertz, Philos. Trans., 1825, 115, 513–583.
61. R. K. Sachs, L. R. Hlatky and P. Hahnfeldt, Math. Comput. Model., 2001, 33, 1297–1305.
62. T. Hillen, H. Enderling and P. Hahnfeldt, Bull. Math. Biol., 2013, 75, 161–184.
63. H. Enderling, A. R. A. Anderson, M. A. J. Chaplain, A. Beheshti, L. R. Hlatky and P. Hahnfeldt, Cancer Res., 2009, 69, 8814–8821.
64. H. Enderling, Adv. Exp. Med. Biol., 2013, 734, 55–71.
65. L. Norton, Breast Dis., 2008, 29, 27–36.
66. L. Norton, Oncologist, 2005, 10, 370–381.
67. L. Norton and J. Massagué, Nat. Med., 2006, 12, 875–878.
68. H. Enderling, L. R. Hlatky and P. Hahnfeldt, Br. J. Cancer, 2009, 100, 1917–1925.
69. C. I. Morton, L. R. Hlatky, P. Hahnfeldt and H. Enderling, Theor. Biol. Med. Modell., 2011, 8, 48.
70. D. L. Chao, J. T. Eck, D. E. Brash, C. C. Maley and E. G. Luebeck, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15034–15039.
71. A. Sottoriva, J. J. C. Verhoeff, T. Borovski, S. K. McWeeney, L. Naumov, J. P. Medema, P. M. A. Sloot and L. Vermeulen, Cancer Res., 2010, 70, 46–56.
72. S. Bao, Q. Wu, R. E. McLendon, Y. Hao, Q. Shi, A. B. Hjelmeland, M. W. Dewhirst, D. D. Bigner and J. N. Rich, Nature, 2006, 444, 756–760.
73. F. Pajonk, E. Vlashi and W. H. McBride, Stem Cells, 2010, 28, 639–648.
74. M. Dean, T. Fojo and S. Bates, Nat. Rev. Cancer, 2005, 5, 275–284.
75. V. Castillo, R. Valenzuela, C. Huidobro, H. R. Contreras and E. A. Castellon, Int. J. Oncol., 2014, 45, 985–994.
76. L. Li and R. Bhatia, Clin. Cancer Res., 2011, 17, 4936–4941.
77. L. N. Abdullah and E. K.-H. Chow, Clin. Transl. Med., 2013, 2, 3.
78. F. Li, H. Tan, J. Singh, J. Yang, X. Xia, J. Bao, J. Ma, M. Zhan and S. T. C. Wong, BMC Syst. Biol., 2013, 7(suppl 2), S12.
79. D. Dingli and F. Michor, Stem Cells, 2006, 24, 2603–2610.
80. M.-J. Kim, R.-K. Kim, C.-H. Yoon, S. An, S.-G. Hwang, Y. Suh, M.-J. Park, H. Y. Chung, I. G. Kim and S.-J. Lee, J. Cell Sci., 2011, 124, 3084–3094.
81. K. Leder, K. Pitter, Q. Laplant, D. Hambardzumyan, B. D. Ross, T. A. Chan, E. C. Holland and F. Michor, Cell, 2014, 156, 603–616.
82. X. Gao, J. T. McDonald, M. Naidu, P. Hahnfeldt and L. R. Hlatky, Stem Cells Int., 2014, 2014, 249309.
83. X. Gao, J. T. McDonald, L. R. Hlatky and H. Enderling, Cancer Res., 2013, 73, 1481–1490.
84. J. Tang, I. Fernandez-Garcia, S. Vijayakumar, H. Martinez-Ruis, I. Illa-Bochaca, D. H. Nguyen, J.-H. Mao, S. V. Costes and M. H. Barcellos-Hoff, Stem Cells, 2014, 32, 649–661.
85. M. H. Barcellos-Hoff, J. Mammary Gland Biol. Neoplasia, 2001, 6, 213–221.
86. J. C. Mills and J. I. Gordon, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 12334–12336.
87. D. F. Quail, M. J. Taylor and L.-M. Postovit, Curr. Stem Cell Res. Ther., 2012, 7, 197–216.
88. Y. Li and J. Laterra, Cancer Res., 2012, 72, 576–580.
89. F. Pajonk and E. Vlashi, Semin. Radiat. Oncol., 2013, 23, 237–241.
90. J. Zhang, C. Niu, L. Ye, H. Huang, X. He, W.-G. Tong, J. Ross, J. Haug, T. Johnson, J. Q. Feng, S. Harris, L. M. Wiedemann, Y. Mishina and L. Li, Nature, 2003, 425, 836–841.
91. H. Landgren and M. A. Curtis, J. Cell. Physiol., 2011, 226, 1–7.
92. T. Sato, J. H. van Es, H. J. Snippert, D. E. Stange, R. G. Vries, M. van den Born, N. Barker, N. F. Shroyer, M. van de Wetering and H. Clevers, Nature, 2011, 469, 415–418.
93. Z. Agur, O. U. Kirnasovsky, G. Vasserman, L. Tencer-Hershkowicz, Y. Kogan, H. Harrison, R. Lamb and R. B. Clarke, PLoS One, 2011, 6, e24225.
94. R. Lamb, M. P. Ablett, K. Spence, G. Landberg, A. H. Sims and R. B. Clarke, PLoS One, 2013, 8, e67811.
95. P. C. Hermann, S. L. Huber, T. Herrler, A. Aicher, J. W. Ellwart, M. Guba, C. J. Bruns and C. Heeschen, Cell Stem Cell, 2007, 1, 313–323.
96. S. A. Mani, W. Guo, M.-J. Liao, E. N. Eaton, A. Ayyanan, A. Y. Zhou, M. Brooks, F. Reinhard, C. C. Zhang, M. Shipitsin, L. L. Campbell, K. Polyak, C. Brisken, J. Yang and R. A. Weinberg, Cell, 2008, 133, 704–715.
97. C. Turner and M. Kohandel, Semin. Cancer Biol., 2012, 22, 374–378.
98. T. Hide, K. Makino, H. Nakamura, S. Yano, S. Anai, T. Takezaki, J.-I. Kuroda, N. Shinojima, Y. Ueda and J.-I. Kuratsu, Neurol. Med. Chir., 2013, 53, 764–772.
99. E. L. Bearer, J. S. Lowengrub, H. B. Frieboes, Y.-L. Chuang, F. Jin, S. M. Wise, M. Ferrari, D. B. Agus and V. Cristini, Cancer Res., 2009, 69, 4493–4501.
100. W. A. Flavahan, Q. Wu, M. Hitomi, N. Rahim, Y. Kim, A. E. Sloan, R. J. Weil, I. Nakano, J. N. Sarkaria, B. W. Stringer, B. W. Day, M. Li, J. D. Lathia, J. N. Rich and A. B. Hjelmeland, Nat. Neurosci., 2013, 16, 1373–1382.
101. A. B. Hjelmeland, Q. Wu, J. M. Heddleston, G. S. Choudhary, J. MacSwords, J. D. Lathia, R. E. McLendon, D. Lindner, A. Sloan and J. N. Rich, Cell Death Differ., 2011, 18, 829–840.
102. A. Sottoriva, P. M. A. Sloot, J. P. Medema and L. Vermeulen, Cell Cycle, 2010, 9, 1472–1479.
103. A. R. A. Anderson, Math. Med. Biol., 2005, 22, 163–186.
104. J. G. Scott, A. B. Hjelmeland, P. Chinnaiyan, A. R. A. Anderson and D. Basanta, PLoS Comput. Biol., 2014, 10, e1003433.
105. S. N. Gentry and T. L. Jackson, PLoS One, 2013, 8, e71128.
106. M. S. Wicha, S. Liu and G. Dontu, Cancer Res., 2006, 66, 1883–1890 , discussion 1895–1896.
107. A. D. Lander, J. Biol., 2009, 8, 70.
108. M. Rahman, L. Deleyrolle, V. Vedam-Mai, H. Azari, M. Abd-El-Barr and B. A. Reynolds, Neurosurg., 2011, 68, 531–545 , discussion 545.
109. T. Yang, K. Rycaj, Z.-M. Liu and D. G. Tang, Cancer Res., 2014, 74, 2922–2927.
110. M. C. Mackey, in Case Studies in Mathematical Modeling Ecology, Physiology, and Cell Biology, ed. H. G. Othmer, F. R. Adler, M. A. Lewis and J. C. Dallon, Case Studies in Mathematical Modeling, 1997.
111. B. M. Boman, J. Z. Fields, O. Bonham-Carter and O. A. Runquist, Cancer Res., 2001, 61, 8408–8411.
112. Z. Agur, Y. Daniel and Y. Ginosar, J. Math. Biol., 2002, 44, 79–86.
113. F. Michor, T. P. Hughes, Y. Iwasa, S. Branford, N. P. Shah, C. L. Sawyers and M. A. Nowak, Nature, 2005, 435, 1267–1270.
114. R. Ganguly and I. K. Puri, Cell Proliferation, 2006, 39, 3–14.
115. D. Dingli, A. Traulsen and F. Michor, PLoS Comput. Biol., 2007, 3, e53.
116. I. Glauche, M. Cross, M. Loeffler and I. Roeder, Stem Cells, 2007, 25, 1791–1799.
117. D. Wodarz, J. Theor. Biol., 2007, 245, 449–458.
118. F. Michor, J. Clin. Oncol., 2008, 26, 2854–2861.
119. R. Ashkenazi, S. N. Gentry and T. L. Jackson, Neoplasia, 2008, 10, 1170–1182.
120. C. Calmelet, A. Prokop, J. Mensah, L. J. McCawley and P. S. Crooke, Math. Modell. Nat. Phenom., 2010, 5, 40–62.
121. T. Stiehl and A. Marciniak-Czochra, Math. Comput. Model., 2011, 53, 1505–1517.
122. A. Sottoriva, L. Vermeulen and S. Tavaré, PLoS Comput. Biol., 2011, 7, e1001132.
123. L. P. Deleyrolle, G. Ericksson, B. J. Morrison, J. A. Lopez, K. Burrage, P. Burrage, A. Vescovi, R. L. Rietze and B. A. Reynolds, PLoS One, 2011, 6, e15844.
124. G. Driessens, B. Beck, A. Caauwe, B. D. Simons and C. Blanpain, Nature, 2012, 488, 527–530.
125. Z. Sun and N. L. Komarova, Math. Biosci., 2012, 240, 231–240.
126. V. Vainstein, O. U. Kirnasovsky, Y. Kogan and Z. Agur, J. Theor. Biol., 2012, 298, 32–41.
127. J. C. L. Alfonso, N. Jagiella, L. Núñez, M. A. Herrero and D. Drasdo, PLoS One, 2014, 9, e89380.
128. I. A. Rodriguez-Brenes, N. L. Komarova and D. Wodarz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 18983–18988.
129. J. A. Spratt, D. von Fournier, J. S. Spratt and E. E. Weber, Cancer, 1993, 71, 2013–2019.
130. D. Hart, E. Shochat and Z. Agur, Br. J. Cancer, 1998, 78, 382–387.
131. L. Hanin, O. Hyrien, J. Bedford and A. Yakovlev, J. Theor. Biol., 2006, 239, 401–416.
132. J. P. Freyer and R. M. Sutherland, Cancer Res., 1986, 46, 3504–3512.
133. A. Brú, S. Albertos, J. Luis Subiza, J. L. García-Asenjo and I. Brú, Biophys. J., 2003, 85, 2948–2961.
134. T. Roose, P. A. Netti, L. L. Munn, Y. Boucher and R. K. Jain, Microvasc. Res., 2003, 66, 204–212.
135. P. Hahnfeldt, Adv. Exp. Med. Biol., 2013, 734, 19–35.
136. S. Kuang, M. A. Gillespie and M. A. Rudnicki, Cell Stem Cell, 2008, 2, 22–31.

---