Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical micro-spectroscopy of single metallic nanoparticles: quantitative extinction and transient resonant four-wave mixing†
Lukas
Payne
a,
George
Zoriniants
a,
Francesco
Masia
b,
Kenton P.
Arkill
c,
Paul
Verkade
c,
Darren
Rowles
d,
Wolfgang
Langbein
b and
Paola
Borri
*a
aCardiff University School of Biosciences, Museum Avenue, Cardiff CF10 3AX, United Kingdom. E-mail: borrip@cf.ac.uk
bCardiff University School of Physics and Astronomy, The Parade, Cardiff CF24 3AA, United Kingdom
cUniversity of Bristol, Wolfson Bioimaging Facility, University Walk, Bristol BS8 1TD, United Kingdom
dBBI Solutions OEM Ltd, Golden Gate, Ty-Glas Avenue, Llanishen, Cardiff CF14 5DX, United Kingdom
First published on 29th May 2015
Abstract
We report a wide-field imaging method to rapidly and quantitatively measure the optical extinction cross-section σext (also polarisation resolved) of a large number of individual gold nanoparticles, for statistically-relevant single particle analysis. We demonstrate a sensitivity of 5 nm2 in σext, enabling detection of single 5 nm gold nanoparticles with total acquisition times in the 1 min range. Moreover, we have developed an analytical model of the polarisation resolved σext, which enabled us to extract geometrical particle aspect ratios from the measured σext. Using this method, we have characterized a large number of nominally-spherical gold nanoparticles in the 10–100 nm size range. Furthermore, the method provided measurements of in-house fabricated nanoparticle conjugates, allowing distinction of individual dimers from single particles and larger aggregates. The same particle conjugates were investigated correlatively by phase-resolved transient resonant four-wave mixing micro-spectroscopy. A direct comparison of the phase-resolved response between single gold nanoparticles and dimers highlighted the promise of the four-wave mixing technique for sensing applications with dimers as plasmon rulers.
1 Introduction
In the last decade, increasing attention has been devoted to methods for the optical detection of single nano-objects, which do not rely on the object's fluorescence emission, but on its absorption and scattering properties (for a recent review see ref. 1). These characteristics are particularly relevant for weakly luminescent systems, such as metallic nanoparticles (NPs), whose morphology-dependent localized surface plasmon resonances (LSPR) produce large particle polarisabilities and, in turn, large absorption and scattering cross-sections at the LSPR frequency. Notably, these resonances can be exploited to image metallic NPs with high sensitivity, and to probe nanoscale regions in the NP vicinity via the local field enhancement effect. Possible applications range from photonics devices,2 catalysis3 and photovoltaics4 to biomedical imaging,5,6 sensing7–9 and medical therapy.10 For many of these applications, it is essential to have a quantitative knowledge of the linear and nonlinear NP optical properties at the single particle level, beyond traditional ensemble-averaged measurements.A number of approaches have been developed recently to measure the optical extinction cross-section σext (defined as σext = Pext/Ii with Ii the incident intensity and Pext the total power lost, due to both absorption and scattering) of single NPs, and to separate this into the absorption and the scattering cross-section, via σext = σabs + σsca. The scattering cross-section σsca is most commonly measured using dark-field microscopy, which offers the advantage of a wide-field illumination with commercial easy-to-use optical set-ups and detector cameras and, in turn, the rapid observation of a large number of individual NPs simultaneously for statistical analysis. However, the quantification of σsca in absolute units in this technique is usually not reported, since it requires the detailed knowledge of the excitation and collection geometries, or a calibration reference. Moreover, for particles much smaller than the wavelength of light (dipole approximation), σsca decreases with the square of the particle volume, limiting the practical applicability of dark-field microscopy to NPs of moderately large sizes (>20 nm diameter for gold and silver nanospheres1).
A sensitive quantitative method to measure σext uses a spatial modulation micro-spectroscopy (SMS) technique.11 The method was shown to achieve detection of single gold NPs as small as 5 nm in diameter, corresponding to a sensitivity in terms of σext down to about 5 nm2. However, for quantitative determination of σext this method needs a precise knowledge of the modulation amplitude and beam profile at the sample. Moreover it is a modulation-based laser-scanning technique, therefore less amenable to the rapid characterization of a large number of NPs compared to wide-field techniques. Additionally, it requires rather costly and specialized equipment. Similar considerations hold for photothermal imaging (PI),12 another laser-scanning modulation-based technique. Moreover, in PI quantifying the absorption cross-section amplitude in absolute units is not trivial, since absorption is only indirectly detected in photothermal signals through the temperature change in the surrounding medium following NP heating.
We have recently shown a simple wide-field microscopy method with which we measured σext on a large number (>100) of single gold NPs rapidly, quantitatively in absolute units, and without the need for calibration standards or complex modulation techniques.13 In this first demonstration, we showed measurements on gold NPs of 40 nm and 100 nm diameter for proof-of-principle, and a sensitivity in σext of around 500 nm2, limited by the acquisition speed of the consumer color camera used for detection. We also showed that we could characterize the NP asphericity by using linearly polarized illumination, however the measured polarisation dependence was not analyzed quantitatively to extract the geometrical aspect ratio of the NP.
Beyond linear optical properties, we also developed a nonlinear optical technique, which detects single gold NPs via their transient degenerate four-wave mixing (FWM) resonant at the LSPR.6,14 Owing to an interferometric and time-resolved detection, this technique is specific to gold NPs and background-free (contrary to the above mentioned methods), even in highly scattering and fluorescing environments, such as cells and tissue. Notably, rather than providing the absolute value of σext, the technique is sensitive to the change in the NP extinction induced by a short pump pulse at the LSPR. In turn, owing to the phase-sensitivity of the interferometric detection, we showed that we could measure the pump-induced ultrafast change in the particle polarisability as a complex quantity, i.e. separating its real and imaginary parts.14 The phase of this complex quantity was shown to be sensitive to the relative shift between the LSPR and the optical wavelength in the FWM experiment. Hence, beyond fundamental interest, this background-free, phase-resolved, intrinsic ratiometric readout, at the single-particle level, could be exploited for LSPR-based sensing applications, for example using NP dimers as plasmon rulers.9
In this work, we report a major improvement on our previous wide-field extinction microscopy method, which now enables us to reach a sensitivity in σext of about 5 nm2, hence allowing detection of single 5 nm diameter gold NPs. The technique remains rapid, wide-field, and easy to implement on any conventional microscope. We also present a method to extract the nanoparticle geometrical aspect ratio from the measured polarisation-resolved σext using analytical formulas for elliptical particles. With this wide-field extinction technique, we have characterized a statistically significant number of gold NP conjugates fabricated in house, and used the measurements to distinguish single dimers from isolated particles and larger aggregates. We then performed FWM measurements on the same NP conjugates, allowing direct correlation with the optical extinction method. The results highlighted the promise of the FWM technique for sensing applications.
2 Wide-field extinction microscopy
2.1 Isolated quasi-spherical nanoparticles
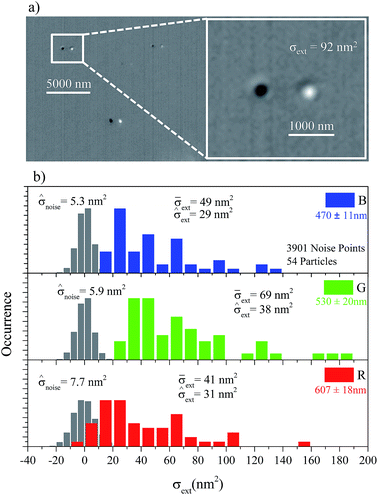
The experimental set-up consists of an inverted microscope (Nikon Ti-U) equipped with a white-light illumination (halogen lamp 100 W with Nikon neutral color balance filter or light balancing LB200 optical blue Hoya filter), an oil condenser of 1.4 numerical aperture (NA) with a removable home-built dark-field illumination of 1.1–1.4 NA, a choice between a 40× 0.95 NA dry objective and a 100× 1.45 NA oil objective, 1× or 1.5× intermediate (tube lens) magnification, a consumer Canon EOS 40D color camera attached to the left port of the microscope and the PCO Edge 5.5, a low noise, high frame-rate, grayscale (b/w), water-cooled, scientific-CMOS camera (sCMOS), attached to the eye-piece side port. With the Canon camera, images were taken in Canon 14-bit RAW format with 10.1 megapixel resolution. The RAW images were converted using the DCRAW plugin in ImageJ, providing 16 bit RGB images with a linear response to intensity and no color balancing. The color camera enables a coarse spectroscopic detection, separating the three wavelength ranges of red (R) 570–650 nm, green (G) 480–580 nm, and blue (B) 420–510 nm. With the sCMOS camera, spectroscopic detection was achieved using bandpass filters (Semrock) in the excitation beam path, in the wavelength ranges of 470 ± 11 nm for blue, 530 ± 20 nm for green and 607 ± 18 nm for red.The investigated samples were nominally spherical gold NPs of 10 nm, 30 nm, 40 nm, 60 nm, 80 nm and 100 nm diameter (BBI Solutions) drop cast onto a glass coverslip, covered in silicone oil (refractive index n = 1.518) and sealed with a glass slide. Before use, glass slides and coverslips were cleaned thoroughly to avoid debris. Cleaning was performed first with acetone and high-quality cleanroom wipes, followed by a chemical etch called Caro's etch, or more commonly, Piranha etch.
Extinction microscopy was performed as described in ref. 13. Briefly, the condenser NA was adjusted to match that of the objective. Two bright-field images were taken; one with the NPs in focus, and another with the NPs either out-of-focus (moving the objective by approximately d = 15 μm axially away from the sample) or laterally shifted by approximately 1 μm. Background images were taken for blocked illumination. To achieve the lowest shot noise with the Canon camera, the lowest camera sensitivity was used (100 ISO), for which the full-well capacity of the pixels of about Nfw = 4 × 104 electrons occurs at 70% of the digitizer range (3.4 electrons per count). An exposure time in the order of 10 ms was chosen to reach Nfw. Averaging over Na = 36 acquisitions was performed for each image set. With the sCMOS, we had Nfw = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electrons (0.54 electrons per count, 16 bit dynamic range), an exposure time of 1 ms and Na = 25
000 electrons (0.54 electrons per count, 16 bit dynamic range), an exposure time of 1 ms and Na = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 at 400 frames per s, resulting in a total acquisition time of 64 s for an image set.
600 at 400 frames per s, resulting in a total acquisition time of 64 s for an image set.
We call the background-subtracted, transmitted intensity of the bright-field image with NPs in focus If, and the defocused, or shifted, intensity I0. In the defocused image, a NP distributes its effect over a radius of about rd = NAd, making I0 similar to the intensity If in the absence of the NP. In the shifted image, we directly measure the intensity in the absence of the NP, which has been sideways shifted from its location. The extinction cross-section of a NP located within the area Ai in the image can then be expressed as 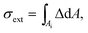 with the relative extinction Δ = (I0 − If)/I0. To account for the slight mismatch between I0 and If without a NP due to, for example, a drift of the illumination intensity, the residual influence of the NP out-of-focus, and/or a non-perfect optical quality of the glass surface, we determine a local background extinction
with the relative extinction Δ = (I0 − If)/I0. To account for the slight mismatch between I0 and If without a NP due to, for example, a drift of the illumination intensity, the residual influence of the NP out-of-focus, and/or a non-perfect optical quality of the glass surface, we determine a local background extinction 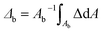 in the area Ab between the radius ri and 2ri, yielding the background-corrected
in the area Ab between the radius ri and 2ri, yielding the background-corrected 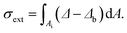 As discussed in ref. 13, a good choice of ri, for which saturation of σext is reached, is given by ∼3λ/(2 NA), approximately at the second Airy ring of the objective point-spread function.
As discussed in ref. 13, a good choice of ri, for which saturation of σext is reached, is given by ∼3λ/(2 NA), approximately at the second Airy ring of the objective point-spread function.
In order to determine σext of many particles from an extinction image, we developed an image analysis programme written in ImageJ macro language, as described in ref. 13 (updated version available). Isolated spherical NPs are distinguished using their extinction color. NPs with σext largest in the color channel corresponding to the expected plasmon resonance are retained, i.e. green (red) for 10–40 nm (100 nm) spherical gold NPs having a LSPR dominated by the absorption (scattering) part of the extinction at around 540 nm (∼590 nm) in a surrounding medium of 1.5 refractive index. NPs which likely correspond to aggregates, debris, or largely non-spherical NPs are excluded in this way. NPs of 60 nm and 80 nm nominal diameter have a size range distribution which allows for isolated particles to have a σext largest in either the green or the red channel of the Canon camera. This was taken into account in the image analysis automated routine. The statistical results over 54 individual gold NPs of nominally 10 nm diameter are summarised in Fig. 1, measured using the 100× 1.45 NA oil objective, the sCMOS camera, and by laterally shifting the sample for reference. An example of an extinction image is shown in Fig. 1a, demonstrating the high contrast in visualizing single 10 nm NPs (which appear as two spots, one bright and one dark, due to the lateral shifting). We adopted a “time-symmetric referencing” procedure, namely I0 was measured before and after If and its average value was used for reference. This reduces the effect of slow drifts. The distribution of σext in the G channel corresponding to the plasmon resonance has a mean of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ext = 69 nm2, which is consistent with experimental and theoretical values found in the literature.15,16 The measurement noise in the experiment,
ext = 69 nm2, which is consistent with experimental and theoretical values found in the literature.15,16 The measurement noise in the experiment, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise, is obtained from the standard deviation of the zero-mean distribution of σext in image regions free of NPs. As shown in Fig. 1, we find
noise, is obtained from the standard deviation of the zero-mean distribution of σext in image regions free of NPs. As shown in Fig. 1, we find ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise = 5.9 nm2 for the green channel, and down to
noise = 5.9 nm2 for the green channel, and down to ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise = 5.3 nm2 in the blue channel. Notably, this number is two orders of magnitude lower than what was shown in our previous work using the consumer Canon camera. The main reason for such reduction of
noise = 5.3 nm2 in the blue channel. Notably, this number is two orders of magnitude lower than what was shown in our previous work using the consumer Canon camera. The main reason for such reduction of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise is the large number of averages (Na = 25
noise is the large number of averages (Na = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600) possible with the high-speed sCMOS camera, while retaining a practically feasible total acquisition time over which setup drifts are acceptable. The experimental
600) possible with the high-speed sCMOS camera, while retaining a practically feasible total acquisition time over which setup drifts are acceptable. The experimental ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise is, however, still larger than the theoretical shot-noise limit of 3 nm2, as estimated using the expression in ref. 13. This is likely due to a non-perfect referencing in the measurement of the extinction image Δ, namely I0 not being identical to the intensity If in the absence of the NP, even with local background correction. To that end, we find that defocusing the objective gives
noise is, however, still larger than the theoretical shot-noise limit of 3 nm2, as estimated using the expression in ref. 13. This is likely due to a non-perfect referencing in the measurement of the extinction image Δ, namely I0 not being identical to the intensity If in the absence of the NP, even with local background correction. To that end, we find that defocusing the objective gives ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise = 25 nm2 compared to
noise = 25 nm2 compared to ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise = 5.9 nm2 when laterally shifting the sample (under otherwise identical conditions), most likely because a lateral shift does not alter the beam path geometry and thus enables a better referencing. We also find
noise = 5.9 nm2 when laterally shifting the sample (under otherwise identical conditions), most likely because a lateral shift does not alter the beam path geometry and thus enables a better referencing. We also find ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise = 7 nm2 when laterally shifting but without time symmetric referencing, indicating that sample/objective/camera drifts play a role. Furthermore, at this sensitivity, the spatial and optical quality of the glass surface provides a spatial extinction structure which contributes to
noise = 7 nm2 when laterally shifting but without time symmetric referencing, indicating that sample/objective/camera drifts play a role. Furthermore, at this sensitivity, the spatial and optical quality of the glass surface provides a spatial extinction structure which contributes to ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise.
noise.
In the histogram in Fig. 1, the standard deviation of σext is much larger than ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise and is dominated by the NP size/shape/environment distribution. The NP-related standard deviation,
noise and is dominated by the NP size/shape/environment distribution. The NP-related standard deviation, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext, is determined using
ext, is determined using ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext2 =
ext2 = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) total2 −
total2 − ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) noise2, where
noise2, where ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) total is the total standard deviation of σext as measured. Using δR/R =
total is the total standard deviation of σext as measured. Using δR/R = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext/(3
ext/(3![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ext), we then inferred a size distribution δR/R = 0.18 (R is the NP radius). This value is larger than the manufacturer specified distribution δR/R = 0.10, as determined by electron microscopy. This suggests, consistent with the literature, that additional factors influence the optical
ext), we then inferred a size distribution δR/R = 0.18 (R is the NP radius). This value is larger than the manufacturer specified distribution δR/R = 0.10, as determined by electron microscopy. This suggests, consistent with the literature, that additional factors influence the optical ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext, beyond size fluctuations, such as the NP asphericity,17 fluctuations in the local dielectric environment, and the electron-surface scattering damping parameter.16
ext, beyond size fluctuations, such as the NP asphericity,17 fluctuations in the local dielectric environment, and the electron-surface scattering damping parameter.16
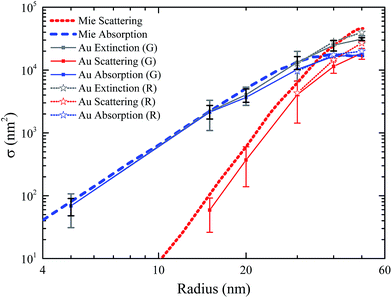
An overview of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ext and
ext and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext in the green color channel for NPs in the 10–60 nm diameter range, and both green and red channels for 60 nm, 80 nm and 100 nm sized NPs, is shown in Fig. 2. Measurements for NPs in the 30–100 nm size range were performed using the 40× 0.95 NA objective, 1.5 magnifier and the consumer Canon camera, as described in ref. 13. For each nominal diameter, a statistical analysis on >50 individual gold NPs was performed. The bars indicate the standard deviation
ext in the green color channel for NPs in the 10–60 nm diameter range, and both green and red channels for 60 nm, 80 nm and 100 nm sized NPs, is shown in Fig. 2. Measurements for NPs in the 30–100 nm size range were performed using the 40× 0.95 NA objective, 1.5 magnifier and the consumer Canon camera, as described in ref. 13. For each nominal diameter, a statistical analysis on >50 individual gold NPs was performed. The bars indicate the standard deviation ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext. We also measured σsca using dark-field, as described in ref. 13, and in turn deduced σabs from σext, as shown in Fig. 2. Note that for these data the calibration constant η (such that
ext. We also measured σsca using dark-field, as described in ref. 13, and in turn deduced σabs from σext, as shown in Fig. 2. Note that for these data the calibration constant η (such that 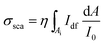 with Idf scattered intensity in dark-field) was measured by using nanodiamonds,18 which are scattering-only particles, where σsca = σext. A comparison between the experimental values and calculations from Mie theory15 of σsca and σabs at the LSPR wavelength is shown in Fig. 2, indicating good agreement (note how for the largest particles the scattering cross-section in the R channel dominates). Deviations between experiment and theory could be due to the spectral averaging of the color channel bandwidth, especially when using the consumer Canon camera. Furthermore, as mentioned in ref. 13, the finite angular range of the objective implies an underestimate of the extinction. In Fig. 2 we also compare
with Idf scattered intensity in dark-field) was measured by using nanodiamonds,18 which are scattering-only particles, where σsca = σext. A comparison between the experimental values and calculations from Mie theory15 of σsca and σabs at the LSPR wavelength is shown in Fig. 2, indicating good agreement (note how for the largest particles the scattering cross-section in the R channel dominates). Deviations between experiment and theory could be due to the spectral averaging of the color channel bandwidth, especially when using the consumer Canon camera. Furthermore, as mentioned in ref. 13, the finite angular range of the objective implies an underestimate of the extinction. In Fig. 2 we also compare ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext with the manufacturer specified size distribution (black error bars) using δR/R =
ext with the manufacturer specified size distribution (black error bars) using δR/R = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext/(
ext/(![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) extγ) with γ = 3 for small particles, where the extinction is dominated by absorption. For particle sizes larger than 40 nm diameter, γ, such that σext ∝ Rγ, was extracted from σext calculated from Mie theory using the sum of σsca and σabs at the corresponding LSPR wavelength. We find that
extγ) with γ = 3 for small particles, where the extinction is dominated by absorption. For particle sizes larger than 40 nm diameter, γ, such that σext ∝ Rγ, was extracted from σext calculated from Mie theory using the sum of σsca and σabs at the corresponding LSPR wavelength. We find that ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext is generally larger than the manufacturer specifications, again suggesting that additional factors influence the optical
ext is generally larger than the manufacturer specifications, again suggesting that additional factors influence the optical ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ext, beyond size fluctuations.
ext, beyond size fluctuations.
2.2 Nanoparticle asphericity
In our previous work, we showed that by measuring the dependence of σext on the in-plane linear polarisation angle θ of the exciting light we could extract information on the NP asphericity.13 In particular, we fitted the experimental σext with the expression σext(θ) = σ0(1 + αP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2(θ − θ0))), where σ0 is the polarisation-averaged σext, αP ≥ 0 is the amplitude of the polarisation dependence, and 0 ≥ θ0 ≥ π is an angular offset, indicating the orientation (in-plane) of the NP asymmetry. We found that, within the measurement noise, aspherical NPs could be identified as those having αP larger than about 0.1 (in the red channel). However, the relationship between αP and the particle aspect-ratio was not derived, hence this parameter remained a phenomenological value rather than a useful structural quantity. Here we have developed a theoretical model for aspherical particles, with which we have simulated σext(θ) and, in turn, calculated αP as a function of the particle aspect ratio.
cos(2(θ − θ0))), where σ0 is the polarisation-averaged σext, αP ≥ 0 is the amplitude of the polarisation dependence, and 0 ≥ θ0 ≥ π is an angular offset, indicating the orientation (in-plane) of the NP asymmetry. We found that, within the measurement noise, aspherical NPs could be identified as those having αP larger than about 0.1 (in the red channel). However, the relationship between αP and the particle aspect-ratio was not derived, hence this parameter remained a phenomenological value rather than a useful structural quantity. Here we have developed a theoretical model for aspherical particles, with which we have simulated σext(θ) and, in turn, calculated αP as a function of the particle aspect ratio.
We describe a non-spherical particle as a metallic ellipsoid with three orthogonal semi-axes a, b and c. In the particle reference system, the polarisability tensor ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) is diagonal, and its eigenvalues (in the limit of particles with a radius much smaller than the light wavelength) are given by19
is diagonal, and its eigenvalues (in the limit of particles with a radius much smaller than the light wavelength) are given by19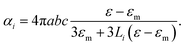 ε is the dielectric constant of gold, εm is the dielectric constant of the medium surrounding the NP, and Li with i = a, b, c are dimensionless quantities defined by the particle geometry (see ESI†). We then expressed σext as a function of
ε is the dielectric constant of gold, εm is the dielectric constant of the medium surrounding the NP, and Li with i = a, b, c are dimensionless quantities defined by the particle geometry (see ESI†). We then expressed σext as a function of ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) , taking into account that for an arbitrary particle orientation in the laboratory system, the polarisability tensor is
, taking into account that for an arbitrary particle orientation in the laboratory system, the polarisability tensor is 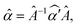 where  is the rotation matrix transforming the particle reference system into the laboratory system, and α′ is the polarisability tensor in the laboratory system. The absorption, scattering, and extinction cross-sections are calculated following ref. 19 (for more details see ESI†). If the polarisation of light is parallel to one of the symmetry axes of the particle, the extinction cross-section is given by:
where  is the rotation matrix transforming the particle reference system into the laboratory system, and α′ is the polarisability tensor in the laboratory system. The absorption, scattering, and extinction cross-sections are calculated following ref. 19 (for more details see ESI†). If the polarisation of light is parallel to one of the symmetry axes of the particle, the extinction cross-section is given by:
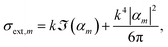 | (1) |
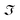 denotes the imaginary part. If the particle is oriented in-plane at an angle γ with respect to the laboratory x-axis, the extinction cross-section for an incident polarized light in-plane at an angle θ with respect to the laboratory x-axis can be accordingly calculated using the rotation matrix Â, and is found to be (for details see ESI†):
denotes the imaginary part. If the particle is oriented in-plane at an angle γ with respect to the laboratory x-axis, the extinction cross-section for an incident polarized light in-plane at an angle θ with respect to the laboratory x-axis can be accordingly calculated using the rotation matrix Â, and is found to be (for details see ESI†):σext(θ) = σext,1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(γ − θ) + σext,2 cos2(γ − θ) + σext,2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(γ − θ) sin2(γ − θ) | (2) |
This represents a sinusoidal dependence of the measured extinction cross-section versus θ, which can be rewritten as:
σext(θ) = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (1 + αP (1 + αP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[2(θ − γ)]) cos[2(θ − γ)]) | (3) |
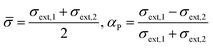 | (4) |
With these formulas, for a non-spherical particle with in-plane asymmetry a > b (note that in the experiment we are not sensitive to the asymmetry in the z-axis), we calculated αP and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) as a function of the particle ellipticity parameter 1 − b/a and the particle volume (4/3)πabc (where we used
as a function of the particle ellipticity parameter 1 − b/a and the particle volume (4/3)πabc (where we used 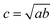 ). We find that in the limit of small ellipticity (αP < 0.5), αP is proportional to the ellipticity parameter and is almost independent of the particle volume (see ESI†). Thus, the ellipticity can be simply determined as 1 − b/a = KαP with the parameter K being a function of the wavelength range used in the experiment. For the G and R channels of the Canon 40D camera used in ref. 13, we find KG = 0.568 and KR = 0.339. Therefore a measured αP = 0.1 in the R channel corresponds to an ellipticity 1 − b/a of 3.39%.
). We find that in the limit of small ellipticity (αP < 0.5), αP is proportional to the ellipticity parameter and is almost independent of the particle volume (see ESI†). Thus, the ellipticity can be simply determined as 1 − b/a = KαP with the parameter K being a function of the wavelength range used in the experiment. For the G and R channels of the Canon 40D camera used in ref. 13, we find KG = 0.568 and KR = 0.339. Therefore a measured αP = 0.1 in the R channel corresponds to an ellipticity 1 − b/a of 3.39%.
2.3 Nanoparticle dimers
We investigated the applicability of this wide-field imaging method to the characterization of gold NP dimers fabricated in-house. Nominally spherical 40 nm diameter gold NPs coated with a nominal 6 nm thick silica shell were fabricated by BBI Solutions. We covalently bound them to bare 40 nm gold NPs in solution using (3-mercaptopropyl)trimethoxysilane (3-MT). Briefly, this was achieved by mixing equal volumes (250 μl each) of bare and silica-coated NPs stock solutions (each at a concentration of approximately 9 × 109 NP per ml) with 0.985 ml of water (Millipore) and 15 μl of 3-MT. The dimerisation reaction was monitored in real-time through the occurrence of a shifted LSPR peak using absorbance spectroscopy and the reaction was stopped (typically after 2 min) using N-ethylmaleimide. Examples of the type of dimers obtained in this way are shown in the transmission electron microscopy (TEM) images in Fig. 3. For TEM imaging, 5 μl of the solution containing gold NP dimers was drop cast onto a TEM grid (3 mm diameter, 200 mesh amorphous holey carbon-coated copper grid (EM Resolutions)). The grid was then imaged using a 200 keV LaB6 filament transmission electron microscope (Tecnai T20, FEI) with a 4096 × 4096 pixel 16 bit bottom-mounted camera (BM Eagle, FEI). For optical measurements, solutions with gold NP dimers were covalently bound onto a glass coverslip functionalised with 3-MT, covered in silicone oil, and sealed with a glass slide. The solution contained a mixture of isolated NPs, dimers and larger aggregates (see overview TEM image – Fig. 3a). We therefore investigated the applicability of our wide-field microscopy method to characterize such a heterogeneous ensemble, and specifically, to distinguish dimers from single particles and larger aggregates.A cloud plot representing a combination of the extinction cross-section σext measured for these NPs on glass in the G and R channels (using the 40× 0.95 NA objective, 1.5 magnifier and the Canon camera) alongside the asymmetry parameter αP (for σsca) in the corresponding channels is shown in Fig. 4. We chose to represent αP extracted from σsca due to its lower uncertainty compared to αP from σext when measuring with the Canon color camera.13 The coordinates were chosen as (i) the extinction cross-section represented by the sum of R and G channels σR + σG, (ii) the G to R cross-section contrast (σG − σR)/(σG + σR), and (iii) the asymmetry ratio αPR/αPG. The cross-section indicates whether particles are single or aggregates, since this value will scale roughly proportional to the number of particles in the focal volume. The differential quantity (σG − σR)/(σG + σR) gives information on the spectral position of the LSPR, where we expect isolated spherical particles to have σG > σR, while dimers and aggregates will have σR > σG due to the red shift of the LSPR upon plasmonic coupling in a dimer with a gap much smaller than the NP diameter.20 The ratio αPR/αPG is used to emphasize the asymmetry due to dimer formation, where we expect αPR/αPG ≳ 1 for a single slightly aspherical particle and αPR/αPG ≫ 1 for dimers with small gaps. We can see a systematic trend in Fig. 4 with isolated particles being the group where (σG − σR)/(σG + σR) > 0, αPR/αPG < 2 and σR + σG < 6000 nm2 (![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ext = 4000 nm2 in the G channel and
ext = 4000 nm2 in the G channel and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ext = 2000 nm2 in the R channel for an isolated 40 nm NP), while strongly coupled dimers are being identified as the group where (σG − σR)/(σG + σR) < 0, αPR/αPG > 2 and 12
ext = 2000 nm2 in the R channel for an isolated 40 nm NP), while strongly coupled dimers are being identified as the group where (σG − σR)/(σG + σR) < 0, αPR/αPG > 2 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 > σR + σG > 6000 nm2. For larger aggregates σR + σG > 12
000 > σR + σG > 6000 nm2. For larger aggregates σR + σG > 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm2, (σG − σR)/(σG + σR) < 0 but αPR/αPG varies, depending on the anisotropy of the assembly. In fact, we see in the cloud plot a large aggregate with αPR/αPG < 2 and σR + σG ∼ 14
000 nm2, (σG − σR)/(σG + σR) < 0 but αPR/αPG varies, depending on the anisotropy of the assembly. In fact, we see in the cloud plot a large aggregate with αPR/αPG < 2 and σR + σG ∼ 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm2, consistent with a closely-packed trimer.
000 nm2, consistent with a closely-packed trimer.
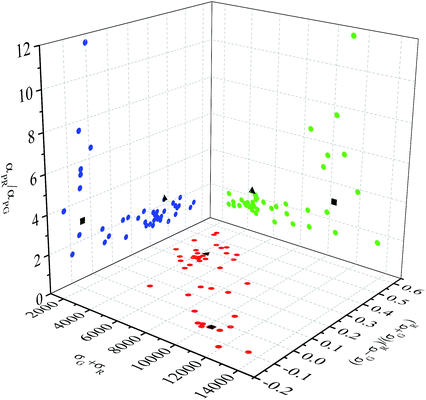 | ||
| Fig. 4 Optical properties measured on individual NPs covalently bound onto glass, from a solution containing nominal 40 nm NPs coated with a 6 nm thick silica shell and covalently bound to bare 40 nm NPs (same as in Fig. 3). Measurements are shown as a trivariate distribution using the cross-section σR + σG, the contrast (σG − σR)/(σG + σR), and the asymmetry parameter ratio αPR/αPG (see text). Black symbols indicate the two particles shown in Fig. 5. | ||
To confirm these attributions, for the two particles highlighted by black symbols in the cloud plot in Fig. 4, we have measured the spectrally-resolved and polarisation-resolved extinction. We inserted a linear polariser in the white-light illumination beam path before the condenser, and coupled the transmitted light collected by the microscope objective (100× 1.45 NA oil objective, 1× intermediate magnification) into an imaging spectrometer (Horiba Jobin-Yvon iHR 550) equipped with a 100 lines per mm grating (input slit opening of 60 μm corresponding to ∼1 nm spectral resolution) and a CCD camera (Andor Newton DU-971N). Referencing was performed similarly to the extinction microscopy discussed in the previous section. Briefly, a stripe-like region of the sample containing a NP in the center was imaged onto the input slit of the spectrometer and, in turn, onto the CCD camera. Within this stripe, image regions above and below the NP were used as a reference under identical spectral illumination conditions. A measurement without the NP (by lateral shifting) was also acquired to correct for irregularities in the camera pixels. Fig. 5a shows the extinction spectra for the particle highlighted as a black triangle in Fig. 4. The spectra exhibit a single LSPR at around 540 nm, almost independent of the polarisation angle, supporting the attribution that this particle is an isolate quasi-spherical NP. Fig. 5b shows the extinction spectra for the particle highlighted as a black square in Fig. 4, which exhibit a strong polarisation dependence and two distinct LSPRs (one at 535 nm and the second one at 575 nm) for two orthogonal polarisations, supporting the attribution that this particle is a dimer. Numerical simulations, using the software COMSOL Multiphysics, of the extinction spectra of a gold dimer surrounded by a homogeneous medium of refractive index 1.5, calculated for the two in-plane polarisations along and perpendicular to the interparticle axis, are shown for comparison (dotted lines in Fig. 5). The best agreement between simulations and the experiment is found assuming that the two NPs forming the dimer have slightly different diameters of 32 nm and 33 nm (heterodimer model) and an interparticle gap of 5.5 nm. Larger diameters result in larger peak cross-sections, while different gaps do not reproduce the red-shifted LSPR wavelength at 575 nm. Using NPs with different diameters enabled us to optimize the amplitude ratio between the longitudinal and transverse plasmon peaks. The deviation between simulations and experiment might be due to the imperfect sphericity of the particles, not included in the calculations. Furthermore, simulations assume an incident plane wave, and do not account for the experimental angular excitation and detection range.
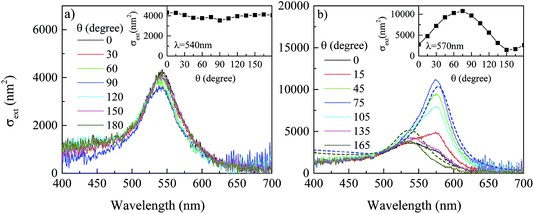 | ||
| Fig. 5 Extinction spectra on the particles indicated as black symbols in Fig. 4 for various in-plane linear polarisation angles θ of the white-light illumination as indicated. The insets show the extinction versus polarizer angle at the indicated wavelength. (a) Spectra on the particle indicated by the black triangle in Fig. 4. (b) Spectra on the particle indicated by the black square in Fig. 4. Dotted lines are numerical simulations of the extinction spectra of a dimer consisting of a spherical NP of 32 nm diameter with a gap distance of 5.5 nm from a second particle of 33 nm diameter, calculated using COMSOL Multiphysics for the two in-plane polarisations along and perpendicular to the interparticle axis. Measured spectra were acquired using an exposure time of 0.1 s, and 200 frames average. | ||
3 Resonant four-wave mixing microscopy
Transient resonant four-wave mixing micro-spectroscopy was performed with a heterodyne interferometric detection very similar to the one discussed in our previous works,6,14 the main difference being that we used an epi-detection geometry instead of a transmission geometry. Briefly, optical pulses of ∼100 fs duration at 80 MHz repetition rate and 550 nm center wavelength were provided by the signal output of an optical parametric oscillator (OPO). The pulse train is split into three beams (pump, probe and reference), having all the same center wavelength (degenerate FWM scheme). The pump beam excites the sample with an intensity which is temporally modulated by an acousto-optic modulator (AOM) driven with a square wave amplitude modulation of about 1 MHz frequency. The change in the sample optical properties induced by this excitation is probed by the probe pulse at an adjustable delay time τ after the pump pulse. Pump and probe pulses of fields E1 and E2, respectively, are recombined into the same spatial mode and focused onto the sample by a microscope objective (for the data shown a 40× 0.95 NA) mounted into the same inverted microscope stand used for the extinction microscopy discussed in the previous section. The sample position is moved relative to the focal volume of the objective by an xyz piezoelectric stage. A FWM signal (proportional to E1E*1E2) is collected in reflection (epi-direction) by the same objective, and recombined in a beam splitter with the reference pulse of adjustable delay. The resulting interference is detected by balanced photodiodes (for common-mode noise rejection) and a dual-channel high-frequency lock-in amplifier. We used a heterodyne scheme where the probe optical frequency is upshifted by a radio-frequency amount using an AOM and its interference with the unshifted reference is detected at the appropriate beat frequency, as in the scheme published in ref. 14. This enables us to discriminate the FWM field from the pump and probe pulses and to detect the amplitude and phase of the field. Full control of the pump, probe and reference polarisation was achieved using waveplates in each beam. Note that this interferometric time-resolved FWM detection enables background-free imaging of single gold NPs even in highly scattering and fluorescing environments.6In Fig. 6a we first recall an example of FWM dynamics versus τ measured on a single NP of nominal 40 nm diameter drop cast onto glass (from ref. 14) alongside the theoretical model discussed in detail in ref. 14. A key point is the ability of the technique to distinguish the real and imaginary part of the pump-induced change in the particle complex polarisability, indicated as Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) R and Δ
R and Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) I, respectively (where we defined an effective dielectric constant
I, respectively (where we defined an effective dielectric constant ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) proportional to the NP polarisability α = 4πR3
proportional to the NP polarisability α = 4πR3![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) for spherical particles, and denoted the pump-induced change as Δ
for spherical particles, and denoted the pump-induced change as Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ). Both Δ
). Both Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) R and Δ
R and Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) I exhibit dynamics that are quantitatively explained by the model. These are due to the pump-induced increase in the electron temperature (which, in turn, broadens and shifts the LSPR on a ∼100 fs time scale), followed by a recovery to equilibrium via the thermalization of the hot electron gas with the cooler lattice by electron–phonon coupling (∼1 ps time scale), and the thermalization of the heated NP with the cooler surroundings (∼100 ps time scale). We also observe coherent phonon oscillations in Δ
I exhibit dynamics that are quantitatively explained by the model. These are due to the pump-induced increase in the electron temperature (which, in turn, broadens and shifts the LSPR on a ∼100 fs time scale), followed by a recovery to equilibrium via the thermalization of the hot electron gas with the cooler lattice by electron–phonon coupling (∼1 ps time scale), and the thermalization of the heated NP with the cooler surroundings (∼100 ps time scale). We also observe coherent phonon oscillations in Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) R (see inset in Fig. 6a). These are due to the modulation of the plasma frequency by the breathing vibrational mode of the NP with an oscillation period proportional to the particle radius21–23 from which we infer a diameter of 38 nm for the specific NP shown.
R (see inset in Fig. 6a). These are due to the modulation of the plasma frequency by the breathing vibrational mode of the NP with an oscillation period proportional to the particle radius21–23 from which we infer a diameter of 38 nm for the specific NP shown.
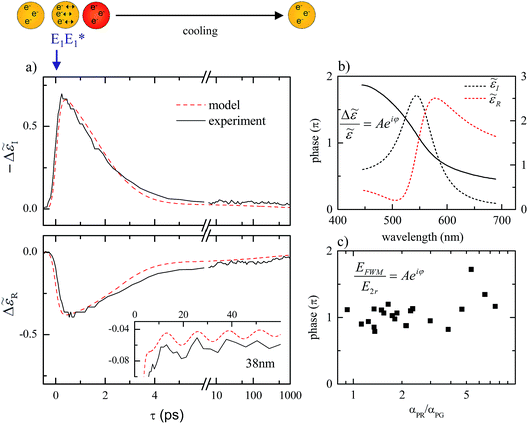 | ||
Fig. 6 a) Transient changes of the real (Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) R) and imaginary (Δ R) and imaginary (Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) I) part of the dielectric function of a single 38 nm diameter gold NP resonantly excited and probed at 550 nm. The pump (probe) fluence is 0.65 J m−2 (0.05 J m−2). The acquisition time per point is 200 ms. The dashed lines are the corresponding calculations. The top sketch illustrates the LSPR excitation by the pump (E1) and the subsequent heating and cooling dynamics monitored by the probe pulse. The inset shows coherent phonon oscillations from which the 38 nm diameter is deduced (reproduced from ref. 14). (b) Spectrally resolved real and imaginary part of the dielectric constant I) part of the dielectric function of a single 38 nm diameter gold NP resonantly excited and probed at 550 nm. The pump (probe) fluence is 0.65 J m−2 (0.05 J m−2). The acquisition time per point is 200 ms. The dashed lines are the corresponding calculations. The top sketch illustrates the LSPR excitation by the pump (E1) and the subsequent heating and cooling dynamics monitored by the probe pulse. The inset shows coherent phonon oscillations from which the 38 nm diameter is deduced (reproduced from ref. 14). (b) Spectrally resolved real and imaginary part of the dielectric constant ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (dotted lines) simulated for the 38 nm NP in (a) prior to the arrival of the pump, together with the phase φ (solid line) of the complex quantity Δ (dotted lines) simulated for the 38 nm NP in (a) prior to the arrival of the pump, together with the phase φ (solid line) of the complex quantity Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) / /![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) with the pump-induced change Δ with the pump-induced change Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) calculated at τ = 0.5 ps. (c) Measured phase of the ratio between the FWM field and the reflected probe at τ = 0.5 ps on a group of NPs from the cloud plot in Fig. 4 as a function of the asymmetry parameter αPR/αPG. calculated at τ = 0.5 ps. (c) Measured phase of the ratio between the FWM field and the reflected probe at τ = 0.5 ps on a group of NPs from the cloud plot in Fig. 4 as a function of the asymmetry parameter αPR/αPG. | ||
Besides these dynamics, we showed in ref. 14 that the phase of Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) is sensitive to the spectral position of the LSPR relative to the probe optical frequency in the experiment. The phase is a ratiometric quantity independent of the signal strength, and therefore could be used for robust LSPR-based sensing applications. Owing to the red-shift of the LSPR occurring in a NP dimer (increasing with decreasing interparticle gap distance20), we would thus expect that this phase measured at 550 nm wavelength in our FWM experiment would gradually change, going from a single quasi-spherical NP to a plasmonically coupled dimer (in a gap-dependent manner). To address this expectation, we measured such phase on the group of NPs identified as single quasi-spherical or dimers in Fig. 4.
is sensitive to the spectral position of the LSPR relative to the probe optical frequency in the experiment. The phase is a ratiometric quantity independent of the signal strength, and therefore could be used for robust LSPR-based sensing applications. Owing to the red-shift of the LSPR occurring in a NP dimer (increasing with decreasing interparticle gap distance20), we would thus expect that this phase measured at 550 nm wavelength in our FWM experiment would gradually change, going from a single quasi-spherical NP to a plasmonically coupled dimer (in a gap-dependent manner). To address this expectation, we measured such phase on the group of NPs identified as single quasi-spherical or dimers in Fig. 4.
Since the experiment is performed in epi-geometry, we are detecting the complex quantity Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) /
/![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) via the ratio between the FWM field EFWM ∝ Δ
via the ratio between the FWM field EFWM ∝ Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) E2 and the reflected probe field E2r ∝
E2 and the reflected probe field E2r ∝ ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) E2 (as opposed to the transmitted probe field E2 in ref. 14). The phase φ of Δ
E2 (as opposed to the transmitted probe field E2 in ref. 14). The phase φ of Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) /
/![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) calculated from Δ
calculated from Δ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) at τ = 0.5 ps for a spherical 40 nm NP (see Fig. 5 in ref. 14) is plotted in Fig. 6b together with the real and imaginary parts of
at τ = 0.5 ps for a spherical 40 nm NP (see Fig. 5 in ref. 14) is plotted in Fig. 6b together with the real and imaginary parts of ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) . From this calculation, we expect to observe φ ∼ π for a NP at resonance and φ > π when probing at shorter wavelengths compared to the LSPR. As shown in Fig. 5, the LSPR of the coupled (longitudinal) plasmon mode in a dimer is significantly red shifted compared to the wavelength at 550 nm used in the FWM experiment. Hence, based on these qualitative considerations, we would expect to observe φ > π in a plasmonically coupled dimer compared to φ ∼ π in a single spherical NP. Fig. 6c shows the measured phase of the ratio EFWM/E2r in a group of NPs from the plot in Fig. 4, as a function of the asymmetry ratio αPR/αPG. Measurements were performed using a circularly polarized pump and probe and a co-circularly polarized reference, rather than linear polarisation as in ref. 14, to enable the excitation of dimers without prior knowledge of their orientation. We observe that NPs with a large asymmetry parameter ratio αPR/αPG > 2, indicating dimers according to Fig. 4, tend to exhibit φ > π compared to single quasi-spherical NPs with αPR/αPG < 2 and φ ∼ π, in agreement with our qualitative expectation. A more in-depth understanding of the measured phase both experimentally and theoretically, including a careful calibration against instrument-related phase offsets in the set-up,14 a confirmation that the measured particles are dimers via correlative TEM, and a more quantitative description of the expected dimer response versus interparticle distance and polarisation configuration is in progress and will be published in a future manuscript.
. From this calculation, we expect to observe φ ∼ π for a NP at resonance and φ > π when probing at shorter wavelengths compared to the LSPR. As shown in Fig. 5, the LSPR of the coupled (longitudinal) plasmon mode in a dimer is significantly red shifted compared to the wavelength at 550 nm used in the FWM experiment. Hence, based on these qualitative considerations, we would expect to observe φ > π in a plasmonically coupled dimer compared to φ ∼ π in a single spherical NP. Fig. 6c shows the measured phase of the ratio EFWM/E2r in a group of NPs from the plot in Fig. 4, as a function of the asymmetry ratio αPR/αPG. Measurements were performed using a circularly polarized pump and probe and a co-circularly polarized reference, rather than linear polarisation as in ref. 14, to enable the excitation of dimers without prior knowledge of their orientation. We observe that NPs with a large asymmetry parameter ratio αPR/αPG > 2, indicating dimers according to Fig. 4, tend to exhibit φ > π compared to single quasi-spherical NPs with αPR/αPG < 2 and φ ∼ π, in agreement with our qualitative expectation. A more in-depth understanding of the measured phase both experimentally and theoretically, including a careful calibration against instrument-related phase offsets in the set-up,14 a confirmation that the measured particles are dimers via correlative TEM, and a more quantitative description of the expected dimer response versus interparticle distance and polarisation configuration is in progress and will be published in a future manuscript.
4 Conclusions
In conclusion, we have developed a rapid and sensitive method to quantitatively measure the optical extinction cross-section of individual nanoparticles using wide-field imaging. The method enables simultaneous acquisition of hundreds of nanoparticles for statistical analysis with a sensitivity limit down to 5 nm2, corresponding to a single 5 nm gold NP, using acquisition times in the 1 min range. An experimental demonstration is shown on single nominally-spherical gold nanoparticles with diameters ranging from 10 nm to 100 nm. Importantly, the method can be implemented cost-effectively on any conventional wide-field microscope and is applicable to any nanoparticle. Furthermore, we have investigated the effect of the particle asphericity on the optical extinction cross-section measured with in-plane linearly polarised light as a function of the polarisation direction, and derived, from theory, a simple expression linking these measurements to the particle aspect ratio. We also fabricated gold NP dimers and showed that the optical extinction cross-section analysis can be used to distinguish plasmonically-coupled dimers from single quasi-spherical NPs and larger aggregates. Finally, we performed transient resonant FWM heterodyne interferometry on the same group of NPs characterized by the optical extinction cross-section analysis. We specifically investigated the phase of the ratio between the FWM field and reflected probe field, which is expected to be sensitive to the relative shift between the nanoparticle LSPR and the optical probe wavelength. A comparison between single NPs and dimers identified from the optical extinction analysis supported this expectation and highlighted the potential of these phase-resolved measurements for LSPR-based sensing applications.Data access
Data access Information about the data created during this research, including how to access it, is available from Cardiff University data archive at http://dx.doi.org/10.17035/d.2015.100095.Acknowledgements
This work was funded by the EPSRC UK Research Council under the grant agreement EP/L001470/1. P.B. acknowledges the EPSRC for her Leadership fellowship award EP/I005072/1 and the Royal Society for her Wolfson Research Merit Award. W.L. acknowledges support by a Leverhulme Royal Society Research Fellowship (Grant no. LT20085).References
- A. Crut, P. Maioli, N. D. Fatti and F. Vallée, Chem. Soc. Rev., 2014, 43, 3921–3956 RSC.
- W. Barnes, A. Deraux and T. Ebbesen, Nature, 2003, 424, 824–830 CrossRef CAS PubMed.
- K. Awazu, M. Fujimaki, C. Rockstuhl, J. Tominaga, H. Murakami, Y. Ohki, N. Yoshida and T. Watanabe, J. Am. Chem. Soc., 2008, 130, 1676–1680 CrossRef CAS PubMed.
- H. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213 CrossRef CAS PubMed.
- L. Cognet, S. Berciaud, D. Lasne and B. Lounis, Anal. Chem., 2008, 80, 2288–2294 CrossRef CAS.
- F. Masia, W. Langbein, P. Watson and P. Borri, Opt. Lett., 2009, 34, 1816–1818 CrossRef.
- K. Kneipp, H. Kneipp, I. Itzkan, R. Dasari and M. Feld, J. Phys.: Condens. Matter, 2002, 14, R597–R624 CrossRef CAS.
- A. McFarland and R. Van Duyne, Nano Lett., 2003, 3, 1057–1062 CrossRef CAS.
- C. Sönnichsen, B. M. Reinhard, J. Liphardt and A. P. Alivisatos, Nat. Biotechnol., 2005, 23, 741–745 CrossRef PubMed.
- C. Ayala-Orozco, C. Urban, M. W. Knight, A. S. Urban, O. Neumann, S. W. Bishnoi, S. Mukherjee, A. M. Goodman, H. Charron, T. Mitchell, M. Shea, R. Roy, S. Nanda, R. Schiff, N. J. Halas and A. Joshi, ACS Nano, 2014, 8, 6372–6381 CrossRef CAS PubMed.
- A. Arbouet, D. Christofilos, N. D. Fatti, F. Vallée, J. R. Huntzinger, L. Arnaud, P. Billaud and M. Broyer, Phys. Rev. Lett., 2004, 93, 127401 CrossRef CAS.
- D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Science, 2002, 297, 1160–1163 CrossRef CAS PubMed.
- L. M. Payne, W. Langbein and P. Borri, Appl. Phys. Lett., 2013, 102, 131107 CrossRef PubMed.
- F. Masia, W. Langbein and P. Borri, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235403 CrossRef.
- M. van Dijk, A. Tchebotareva, M. Orrit, M. Lippitz, S. Berciaud, D. Lasne, L. Cognet and B. Lounis, Phys. Chem. Chem. Phys., 2006, 8, 3486–3495 RSC.
- O. L. Muskens, P. Billaud, M. Broyer, N. D. Fatti and F. Vallée, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205410 CrossRef.
- A. Tcherniak, J. Ha, S. Dominguez-Medina, L. Slaughter and S. Link, Nano Lett., 2010, 10, 1398–1404 CrossRef CAS PubMed.
- I. Pope, L. Payne, G. Zoriniants, E. Thomas, O. Williams, P. Watson, W. Langbein and P. Borri, Nat. Nanotechnol., 2014, 9, 940–946 CrossRef CAS PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-VCH, 1998 Search PubMed.
- P. K. Jain, W. Huang and M. A. El-Sayed, Nano Lett., 2007, 7, 2080–2088 CrossRef CAS.
- C. Voisin, N. D. Fatti, D. Christofilos and F. Vallee, J. Phys. Chem. B, 2001, 105, 2264–2280 CrossRef CAS.
- M. A. van Dijk, M. Lippitz and M. Orrit, Phys. Rev. Lett., 2005, 95, 267406 CrossRef.
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5fd00079c |
| This journal is © The Royal Society of Chemistry 2015 |