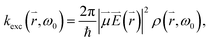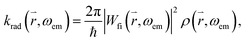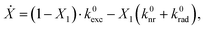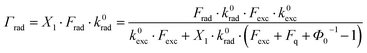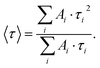Coupling single quantum dots to plasmonic nanocones: optical properties

Abstract

Coupling a single quantum emitter, such as a fluorescent molecule or a quantum dot (QD), to a plasmonic nanostructure is an important issue in nano-optics and nano-spectroscopy, relevant for a wide range of applications, including tip-enhanced near-field optical microscopy, plasmon enhanced molecular sensing and spectroscopy, and nanophotonic amplifiers or nanolasers, to mention only a few. While the field enhancement of a sharp nanoantenna increasing the excitation rate of a very closely positioned single molecule or QD has been well investigated, the detailed physical mechanisms involved in the emission of a photon from such a system are, by far, less investigated. In one of our ongoing research projects, we try to address these issues by constructing and spectroscopically analysing geometrically simple hybrid heterostructures consisting of sharp gold cones with single quantum dots attached to the very tip apex. An important goal of this work is to tune the longitudinal plasmon resonance by adjusting the cones' geometry to the emission maximum of the core–shell CdSe/ZnS QDs at nominally 650 nm. Luminescence spectra of the bare cones, pure QDs and hybrid systems were distinguished successfully. In the next steps we will further investigate, experimentally and theoretically, the optical properties of the coupled systems in more detail, such as the fluorescence spectra, blinking statistics, and the current results on the fluorescence lifetimes, and compare them with uncoupled QDs to obtain a clearer picture of the radiative and non-radiative processes.

---

I. Introduction

Various nanoantennas have been designed to study their influence on the emission properties of single emitters, such as scanning near-field tips,^1–3 single gold nanoparticles,^4,5 discs,⁶ arrays like optical Yagi Uda configurations,⁷ and bowtie antennas.⁸ The positioning of single emitters with high accuracy is a key issue for photonic crystal cavities,⁹ waveguides for single-photon generation,¹⁰ quantum dot lasers¹¹ or nonlinear optical devices.¹² The interaction of quantum emitters in the high near-field region of such metal structures results in energy transfer between the two objects. It is well known that the luminescence and Raman signals of molecules can be enhanced on metal nanostructures, but on the other hand, the radiation of a quantum emitter can also be quenched.^4,5 Tuned to the right wavelength, a plasmonic nanostructure acts as an antenna, leading to an enhancement of the incident exciting radiation, and it can also amplify the reemission from the quantum system.^13,14 In this context, the directionality of coupled systems has also been investigated for more complex nanoantennas.⁷

Nanoscale placement of e.g. quantum dots (QDs) has been demonstrated in the vicinity of metamaterial surfaces¹⁵ or metallic nanostructures.¹⁶ The placement of emitters within the high near-field regions of plasmonic structures requires manipulation with a lateral accuracy of < 10 nm e.g. by optical tweezers¹⁷ or a scanning probe microscope.^18–20 Recently, we developed a straight-forward method, which fulfills the coupling conditions, while all hybrid structures are manufactured at the same time.²¹

The unique optical properties of QDs, such as broad absorption and narrow emission bands, and bright and stable luminescence, make them promising for various applications.²² QDs are very interesting for applications in nanophotonics and quantum optics, in which they serve as single photon sources.²³ They also play an important role as tags and markers in biological sensing.²⁴ Therefore, placing QDs in the hot spot of a gold nanocone tip to investigate the coupling mechanisms between the antenna and the emitter may allow one to understand the basic effects concerning the interaction between a single quantum system and a plasmonic antenna, and moreover, to use gold nanocones as sensor arrays, e.g. for biochemical analysis.²⁵

A. Luminescence and plasmons of gold nanostructures

Luminescence of gold was first reported by Mooradian in 1969, although with a low quantum efficiency of about 10⁻¹⁰.²⁶ According to the band structure, the luminescence can be explained by electron–hole-pair recombination involving the 5d and 6sp bands of gold.²⁷ For rough films and gold nanoparticles, the efficiency increases to 10⁻⁴.^28–30 This behavior has been correlated with the particle size, giving evidence for a relationship with the coherent electron oscillations in metals, the plasmonic modes.³¹ Luminescence can originate directly from the radiative decay of a plasmon oscillation³² or an electron–hole-pair can recombine and release its energy via the plasmon oscillation.³³

Surface-plasmon polaritons are electromagnetic waves in the visible or near infrared region, involving both a coherent oscillation of the conducting electrons, leading to an oscillating charge separation, and a respective electromagnetic wave at the dielectric interface. Both must fulfill the phase-matching condition dictated by the dielectric functions of the respective materials.^34,35 When the particles are smaller than the wavelength, surface-plasmon polaritons cannot propagate any longer and the phase matching condition does not apply. Then, the conducting electron oscillations are defined by the size and shape of the structure, and the particle can act as a resonator forming a standing wave, creating localized surface plasmons or particle plasmons, as they involve the whole nanoparticle.

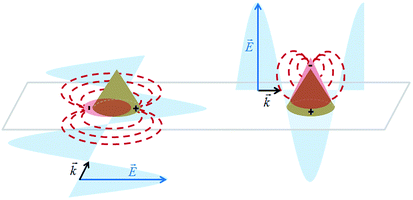
In the case of a gold cone, two types of plasmonic modes can be distinguished: (1) in the transversal direction at the cone base, and (2) in the longitudinal direction, concentrating the electrical field at the tip due to the lightning rod effect as in a SNOM (scanning near-field optical microscopy) tip.³⁶ Two different conditions are illustrated in Fig. 1. Depending on the polarization of the exciting electrical field, either mode can be induced. Note that only one possibility is sketched in Fig. 1 for the transversal plasmonic modes at the cone base.

Fig. 1 Scheme of the gold nanocones excited by the electric field component of an incident electromagnetic wave with different propagation directions. In the left cone, a transversal plasmon mode is excited in the base, while a longitudinal plasmon mode in the right cone is induced, leading to a concentration of the field at the tip of the cone. The directional re-radiation is depicted in a dipole-like fashion.

B. Coupling effects between single emitters and metallic structures

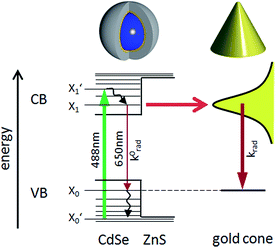
Placing a single molecule or QD in the vicinity of a metallic structure can alter the emission behavior of the emitter. The influence on the radiative and non-radiative decay rates of a QD by a nanoantenna observed via fluorescence intermittency has been a topic of intense study^1,2,37 and several mechanisms are discussed in the literature.^38,39 For describing the interplay between the enhanced excitation due to coupling to the enhanced density of radiative local optical states (LDOS) and quenching due to coupling to the local density of evanescent states, we follow the formalism outlined in ref. 40. We describe the QD's absorption and emission by a four-level system, as shown in Fig. 2.

Fig. 2 Schematic energy level illustration of a CdSe/ZnS-QD coupled to a gold nanocone. First, an electron is excited from the ground state X₀′ of the valence band (VB) with 488 nm radiation to a short lived level X₁′ in the conduction band (CB), from where it relaxes thermally to the state X₁. A QD in free space can either relax radiatively to the ground state X₀ by emitting a photon of about 650 nm or by dissipating its energy to the crystal. If the QD is in close proximity to the tip, its optical near-field couples efficiently to the local optical mode density of a gold cone, which can transfer its energy either to a radiative plasmon mode, which can emit a photon with the rate constant k⁰_rad, or by coupling to evanescent modes, dissipating the energy via ohmic losses in the metal. The non-radiative relaxation paths are not shown in this scheme. The illustration above shows the shell system of the QD, consisting of the CdSe core (blue), the ZnS shell (yellow) and the organic surfactant shell (gray), and a gold cone.

The excitation rate between the electronic ground-state and excited-state, X₀′ and X₁′, respectively, is according to Fermi's golden rule proportional to the square of the electric field 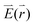amplitude at the position 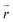of the QD:

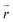with the local density of modes ρ(, ω₀) of the incident photon with energy ω₀ħ matching the gap between X₀′ and X₁′, and the transition dipole moment 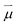connecting the electronic ground state and the excited state. Similarly, the frequency dependent emission rate of a QD between its electronically excited state X₁ and its electronic ground state X₀ is:
where W_fi(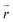, ω_em) is the transition matrix element, i.e. the magnitude of the QD's emission dipole moment. Assuming that the non-radiative relaxation processes from X₁′ to X₁ and X₀ to X₀′ are fast, and X₁′ and X₀ are only occupied for infinitely short times, the relationship X₁ + X₀′ = 1 holds. Hence, the dynamics of the radiative excited state in free space can be described as:
where k⁰_nr is the non-radiative rate in the absence of the gold cone. Thus, the enhanced and localized electric field close to the cone apex can increase the excitation rate of the QD linked to the cone's tip with respect to a flat glass substrate by the enhancement factor 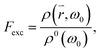where ρ⁰(ω₀) is the density of the optical modes populated by the incident light in free space and ρ(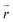, ω₀) is the density of the radiative modes at the tip of the cone. Similarly, the emission of a QD attached to the tip of a cone can be enhanced by the factor 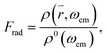where ρ(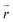, ω_em) is the radiative mode density in close proximity to the cone and ħω_em is the energy of a photon emitted from the QD. In the near-field of the cone, evanescent parts ρ_ev(ω_em) of the mode also exist, which decay within a fraction of the wavelength. These modes are also populated by photons emitted from the QD, leading to energy dissipation in the near-field, and may induce additional radiative losses⁴¹ known as quenching.³⁸ Hence, similar to the enhancement factor, one can also define the quenching factor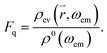

With the modified rate constants and stationary conditions, the total photoluminescence (PL) emission rate of the hybrid system can therefore be expressed as:

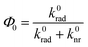where is the free space quantum yield.

II. Optical characterization of pure gold nanocones

In this work we investigate arrays of gold nanocones, which have been fabricated on glass substrates with a thin indium tin oxide (ITO) layer by a procedure similar to those in ref. 42 or ref. 43 and 44. A detailed description of our fabrication process is given in ref. 21.

For studying the emission enhancement of a QD placed on a cone tip, an important issue is to tailor the cone's geometry such that the longitudinal plasmon resonance overlaps with the QD emission which is, according to the manufacturer, around 650 nm.^45,46 For this purpose we have fabricated two kinds of cones: smaller ones with heights of about 111 ± 10 nm and base diameters of 162 ± 10 nm (due to minor variations in the fabrication process), and larger ones with heights of 142 ± 10 nm and base diameters of 164 ± 10 nm. Spectroscopic measurements of single cones were performed with a home-built inverted confocal microscope equipped with a feed-back controlled sample-scanning stage (Physik Instrumente, Karlsruhe, Germany) and an NA 1.46 immersion objective lens (Zeiss, Jena, Germany) for optical excitation and signal collection. Hence, after recording an overview image, we could reproducibly address individual cones or QDs for various spectroscopic measurements. For continuous-wave excitation, either an Ar⁺Kr⁺ laser at λ = 488 nm or a HeNe laser at λ = 632.8 nm was used, focusing the laser spot with a power of 20 μW onto the sample. For recording raster-images, the position dependent PL intensity signal generated in the focus was recorded by a single-photon detector (APD) (Perkin Elmer, SPCM-AQR-14), while the laser excitation is blocked by a long pass filter. Spectra were recorded with an Acton 300 pro spectrometer equipped with a nitrogen cooled SPEC-10 CCD-detector (Princeton Instruments, Trenton, USA).

We prefer azimuthally or radially polarized excitation beams, known also as cylindrical vector beams (CVBs)^47,48 over e.g. linearly polarized Gaussian beams, since they have cylindrical symmetry and give distinct PL excitation patterns when a single molecule or a sub-wavelength nanoparticle is raster scanned through the focal volume, which allow us to visualize directly the orientation of the transition dipole moment or the induced dipole moment. As shown in Fig. 3a (top), an azimuthally polarized laser mode (APM) has a doughnut-shaped field distribution in the focal volume with the electric field component being present exclusively in the focal plane.

Fig. 3 Confocal PL images obtained by raster-scanning gold nanocones (111 nm height, 162 nm base diameter) through the focus of an APM (top) or RPM (bottom). (a) shows the field intensity distribution in the focal volume of an APM (upper panel) with an exclusively transversal electric field component, E_t. In the lower panel, the focal field of an RPM is shown with a longitudinal field component in the center, E_l, surrounded by a radially polarized transversal field, E_t. (b) and (c) show typical PL patterns acquired with two different wavelengths, 632.8 nm and 488 nm, respectively. As the nanocones are smaller than the focus, the sizes of their patterns reflect the electric field distribution in the respective focus. (d) illustrates inhomogeneous PL patterns obtained by an APM for nanocones with a non-circular base, as can be seen in the SEM image below. All white scale bars represent 1 μm.

Raster-scanning a cone with a circular base through such an azimuthal field distribution results in a ring-shaped PL pattern, as shown in Fig. 3b and c (top). A radially polarized laser mode (RPM) forms a focal field with a dominant longitudinal electric field component in the center surrounded by a radially polarized ring. Hence, raster-scanning a sub-wavelength cone through the focal volume results in a bright PL spot in the center surrounded by a less intense ring, as shown in Fig. 3b and c (bottom).

When the nanostructure has a non-circular base, the ring patterns are inhomogeneous, as presented in Fig. 3d. Here, gold nanocones scanned through a focused APM are shown, and they exhibit deviations from the usual uniform patterns. The scanning electron microscope (SEM) image below was acquired by viewing this particular sample from the top to see the shapes of the bases of the structures, which are clearly distorted and look triangular. After acquisition of the SEM images however, the samples are generally contaminated with carbon, showing an intense surface-enhanced carbon Raman spectrum,^49,50 thus obscuring the PL spectra of the single QDs fixed on the cone tips when the hybrid structure is complete. Therefore, the possibility to visualize deviations from the cylindrical shape of the gold nanocones by CVBs without contaminating them is a clear advantage over SEM imaging. The optical characterization via CVBs is absolutely non-destructive as long as low laser powers are used. A comparison of the PL intensities of the patterns obtained with a similar excitation power at 632.8 nm and 488 nm shows that the latter results in a higher maximum intensity. For the cones presented in Fig. 3b, the bright spot in the center excited by the RPM shows twice the intensity compared to the ring from exciting the base of the cone by the APM. These intensity differences between APM and RPM can be explained by examining the spectra in Fig. 4.

Fig. 4 (a) and (b) PL spectra of a smaller cone (115 nm height, 160 nm base diameter) excited with RPM and APM with 488 nm or 632.8 nm wavelength radiation, respectively, normalized to the respective intensity maxima. The insets show the corresponding PL excitation patterns. (c) PL spectra recorded with RPM and APM of a flat gold film. (d) and (e) PL spectra of a taller cone (142 nm height, 160 nm base diameter). (f) Numerical simulations of the longitudinal and transversal plasmon modes performed with COMSOL Multiphysics, showing the location of a bright intensity maximum at the tip for longitudinal excitation and a significantly weaker intensity at the base for transversal excitation. The cone geometry corresponds to the cone presented in (d) and (e) excited by 632.8 nm radiation.

Depending on the aspect ratios and tip radii of the gold nanocones, the intensity ratio between the PL excited by the focused APM and RPM varies. The measurements presented in Fig. 4a and b were performed with the same gold nanocone (111 nm height) excited with the same acquisition time (10 s) and a similar laser power (20 μW), but with different wavelengths and modes. The insets show the corresponding PL excitation patterns. For 488 nm excitation with the RPM, the PL spectrum of this nanocone shows a dominant band at about 520 nm, in agreement with the spectrum of a flat gold film, and a decreasing tail extending from 600 nm to the near infrared region with a barely visible shoulder at 650 nm. Exciting with the APM at 488 nm, the band at 520 nm drops to 40% intensity while the red wavelength tail displays a similar intensity for both polarization modes.

Scanning the same gold nanocone through the focus of an APM and RPM at 632.8 nm (cf.Fig. 4b), we notice for both cases a band at about 660 nm. The spectra of a continuous gold film resulting from excitation by 488 nm radiation reveal no significant difference for excitation by APM or RPM (cf.Fig. 4c). The dominant peak at 520 nm can be assigned to the electron–hole-pair recombination of gold, resulting in a PL emission as described in Section I (A). As for metallic nanostructures where the shape alters the plasmon resonance in contrast to bulk samples, the spectra observed for the gold nanocones differ. The highest peak at 520 nm can be observed by excitation with the RPM, but may shift for different cone heights and aspect ratios, as studied in ref. 36. Upon illuminating the gold nanocone with 488 nm radiation, the strong longitudinal electric field in the focus of an RPM creates an enhanced local field at the cone tip, hence most electron–hole pairs are created right there. The lifetime of electron–hole pairs in bulk gold is only on the order of 10 fs,³² therefore the quantum efficiency for radiative decay is extremely low. However, it is well known that the PL quantum efficiency excited with 632.8 nm radiation on rough Au surfaces and sharp tips is orders of magnitude higher due to the restricted geometry and the longer plasmon lifetime and hence, radiative recombination prevails at the very tip.^51,52 In Fig. 4d and e, respective PL spectra are shown for a taller cone (142 nm height, sharp tip). While the spectra have a similar qualitative shape as in Fig. 4a and b, a clear band appears at 660 nm. This band also appears for 632.8 nm excitation and is definitively missing in the PL spectra of the flat gold film. Therefore, this band may be attributed to the PL decay via the longitudinal plasmon mode of the cone.^53,54

III. Hybrid structures

Core–shell CdSe/ZnS QDs with an emission maximum at nominally 650 nm (purchased from PlasmaChem) were bound to the tips of the cones. The QDs are capped with trioctylphosphine oxide (TOPO) as a stabilizing agent and hexadecylamine (HDA) ligands to link the QDs to the 3-mercaptopropionic acid layer on the cone surface. Binding by thiol chemistry immobilizes the QDs at the cone tips and provides, together with the QD ligands, a spacer of up to 3 nm between the QDs and gold surface. The chemical spacer in combination with the 0.7 nm thick ZnS shell is supposed to provide a sufficient distance to suppress strong PL quenching.⁴ A major challenge is to prevent QDs from binding to the sides of the cone. The selective positioning of QDs at the tips requires temporary embedding of the cones in a resist, which is subsequently removed again. A thin residual resist layer may still be observed on the sample surface. Placing single QDs on the very tips of the cones is by far not trivial and is described in detail in ref. 21.

A. Imaging of hybrid structures

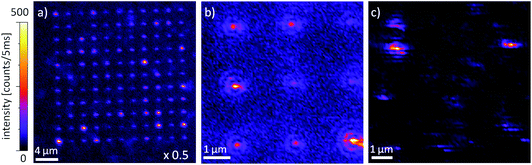
The hybrid structures are arranged in rectangular fields and have been scanned directly after the preparation through the diffraction limited focus of an RPM at 488 nm. According to the optical investigations of all arrays, the number of QDs successfully linked to the gold nanocones can be estimated to be about 70%. The arrays of the hybrid structure exhibit different PL intensities, as presented in Fig. 5a. We can clearly distinguish dim spots and bright spots, the latter ones originating from cones with QDs on the tips.

Fig. 5 Confocal PL excitation images recorded by raster scanning the sample through the focus of an RPM at 488 nm under identical experimental conditions. (a) and (b) show typical patterns of an array of gold cones with QDs at their tips, while (c) exhibits pure QDs on glass, some are bright and show intensity fluctuations typically observed for single quantum systems.

A close-up scan (Fig. 5b) shows seven cones with a weak PL intensity and two structures with bright signals. The image (6 × 6 μm, 100 × 100 pixels) has been recorded with an excitation laser power of 1 μW and an acquisition time of 5 ms per pixel. Usually, for these experimental conditions, the pure gold luminescence from the nanocones is too weak to be detected, but due to the luminescence of the remaining thin layer of the resist, it is also possible to observe the cones without linked QDs. Two structures in Fig. 5b are significantly brighter and show fluorescence intermittency, giving evidence for the presence of single or a few QDs attached to the tips of the cones. Single QDs on a glass substrate (Fig. 5c) typically show significant blinking and an isotropic excitation behavior,⁵⁵ while most of them can barely be observed. Thus, for the majority of QDs, only blurred patterns are detected. In the presented image (Fig. 5c), only three excitation patterns can clearly be identified, showing bright and dark lines typical for line by line scanning of single QDs through a laser focus. In comparison, the bright PL patterns of the hybrid structures exhibit less fluorescence intermittency than single QDs on a pure glass substrate (Fig. 5c). This difference indicates a change in the radiative and non-radiative decay rates of the QDs linked to a gold nanocone.

B. Spectroscopic characterization

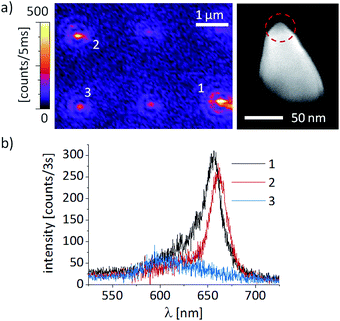
As typical examples, the background corrected spectra from two bright cones displayed in Fig. 6a (labeled 1 and 2) are shown in Fig. 6b. The patterns in Fig. 6a exhibit clear fluorescence intermittency, while a weaker PL pattern (labeled 3) shows no blinking behavior. Cones 1 and 2 feature sharp Lorentzian PL peaks at the wavelength of the QD emission (∼660 nm), indicating that they originate from the luminescence of single or at most a few QDs. Cone 3 features a broad peak at shorter wavelengths with a spectral maximum at about 610 nm, which also appears for cones where no QDs have been fixed and is typical for a thin remaining layer of the resist on the cone. Note that this feature also appears in the spectra of cone 1 and cone 2 as dim short wavelength wings.

Fig. 6 (a) Confocal image of the hybrid structure (left) excited in the focus of a 488 nm RPM. The SEM image (right) shows a typical hybrid structure. Due to the weak contrast, the QD appearing as a small bump at the tip is marked by a dashed circle. The corresponding spectra of individual cones labeled 1, 2 and 3 are presented in (b), where the difference between cones with CdSe/ZnS QDs (spectra 1 and 2) and the cone without a QD (spectrum 3) can clearly be recognized.

A similar very weak PL spectrum of the remaining resist can also be seen on the substrate in between the cones. Indeed, one challenging issue in preparing gold cones with single QDs is to carefully and completely remove traces of the remaining resist since its luminescence may obscure the QD emission. However, such traces are easy to recognize since their spectra are broader and blue shifted with respect to those of QDs and, most importantly, they do not blink. The SEM image of a typical hybrid structure is presented in Fig. 6a (right). To see the QDs linked to the tips of the gold nanocones in the SEM images, the sample has been tilted. Due to the weak material contrast in SEM images, it is difficult to quantify the number of QDs on the cones directly, and the images exhibit only a bump with weak contrast, indicating a QD. One way to estimate the number of QDs coupled to a nanocone is by comparing the spectra of different hybrid structures, such as 1 and 2 in Fig. 6. A typical fit of a cone with most likely only one QD attached is shown in Fig. 7c, which is the spectrum for hybrid 2 in Fig. 6b. It can be very well described by a single Lorentzian with a full-width-at-half-maximum (FWHM) of 19.8 nm, which is in good agreement with the average value we find for single QDs on glass (cf.Fig. 7f). The spectrum for hybrid structure 1 in Fig. 6b shows significant broadening and can only be fitted nicely with two slightly separated, superimposed Lorentzians (not shown), indicating that it originates from more than one QD. For both cases 1 and 2, an additional Gaussian centered at ∼610 nm accounts for the short wavelength tail of the spectra of the cones without QDs, as indicated by spectrum 3 in Fig. 6b.

Fig. 7 Series of spectra of (a) one single QD on a glass cover slide, (b) a single QD linked to the tip of a gold nanocone, (d) a single QD embedded in a PMMA matrix and (e) a gold cone without linked QDs where the PL originates from some residual resist. All spectra were recorded with the same experimental conditions (excitation power of 1 μW at 488 nm, 3 seconds integration time) and fitted to Lorentzian line profiles. For each spectral series, the residuals are shown for one spectrum and they demonstrate the high quality of the fits. A typical fit of a Lorentzian to the spectrum of a single QD on a gold cone is shown in (c) with a Gaussian accounting for the background of the resist and for the spectrum of a single QD on glass, as shown in (f).

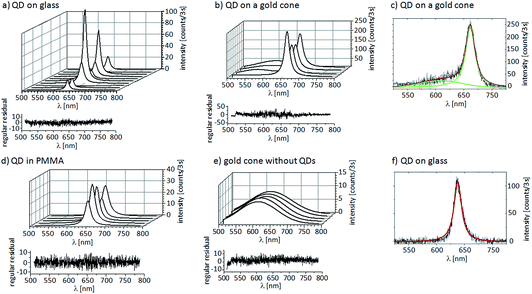
In Fig. 7a, a typical spectral sequence of one single QD deposited on a glass cover slide is shown, together with a spectral sequence of one single QD attached to the tip of a gold cone in Fig. 7b. For comparison, a spectral sequence of one single QD embedded in a thin PMMA film is shown in Fig. 7d. As a reference, a sequence from a gold cone without QDs showing only the background of the resist is displayed in Fig. 7e. All spectra were obtained by exciting with the focus of an RPM at 488 nm and an excitation power of 1 μW with an integration time of 3 seconds. Under these weak excitation conditions, the luminescence of bare gold cones is below the detection limit (see also Fig. 4). For the QD on the gold cone, we observe the highest average spectral intensity of 175 ± 47 counts and an average FWHM of the spectra of 18.84 ± 0.96 nm. The spectra are centered at 650 ± 10 nm, i.e. in resonance with the gold cones. For the QD deposited on the glass surface, the spectra also display Lorentzian line profiles. However, we observe large fluctuations in the intensity maxima from 10 counts to almost 120 counts, with an average of 38 ± 38 counts within one spectral series of the same QD. Here the spectral intensity maximum lies at 638 ± 10 nm and the FWHM is 13.91 ± 2.47 nm. We have also recorded spectra of QDs embedded in a PMMA matrix to protect them from air, as shown in Fig. 7d, and we observe an average intensity of 27 ± 7 counts and a FWHM of 18.81 ± 2.11 nm. Here we see less dramatic intensity fluctuations than for the example on the glass slide without a protective layer. To confirm this different spectral behavior, we have measured and analyzed the spectra for 51 QDs attached to the tips of gold cones that indicate single QD behavior and 78 QDs deposited on glass cover slides.

The statistical analysis is shown in Fig. 8. On glass, the PL-maximum of the QDs is symmetrically distributed around 639 ± 13 nm and the spectra have a FWHM of 19 ± 6 nm. For the QDs attached to the gold cones, the PL is red-shifted by about 10 nm, distributed around 648 ± 11 nm, and the FWHM is slightly larger, i.e. 21 ± 7 nm. Furthermore, the average spectrally integrated intensity of the QDs on the gold cones is 32 ± 15 kcounts/3 s and for the bare QDs on glass cover slides we find 7 ± 6 kcounts/3 s. Comparing the two distributions in Fig. 8b, we see that the QDs on gold cones can be up to an order of magnitude brighter than the QDs on glass. This lets us conclude that the gold cones enhance the PL of the QDs, which agrees well with a similar PL enhancement found in the ensemble of CdSe/ZnS-QDs on rough gold films.^56,57

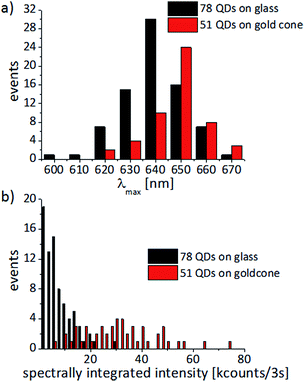Fig. 8 (a) Spectral distribution of the intensity maxima and (b) the spectrally integrated intensity for single CdSe/ZnS-QDs dispersed on a glass cover slide (black) or attached to the tips of individual gold nanocones (red). The statistics are based on 51 QDs on gold cones and 78 QDs on glass cover slides, which all show typical single-molecule spectral behaviour, such as narrow PL-spectra fitted by Lorentzian line profiles and PL-intermittency as shown in Fig. 6 and 7. Wider spectra indicating that they may originate from more than one QD are not considered in the distributions.

C. Time-correlated single photon counting measurements

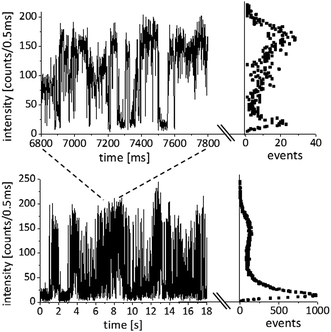
Intensity trajectories showing the emission intermittency of the spectrally integrated PL signal are often used in single-molecule/QD spectroscopy to prove the presence of a single quantum system. However, the blinking statistics of QDs can be very rich, involving multi-exciton decay^58–60 and charge trapping,^61,62 and are still the subject of an on-going scientific debate. The time trace shown in Fig. 9 is typical for a single QD attached to the tip of a gold cone and illustrates the blinking behaviour, which seems to persist in the hybrid systems we have investigated so far. Intensity trajectories were recorded with an APD (Perkin Elmer, SPCM-AQR-14) followed by single photon counting electronics. Here we show a time interval of 18 seconds with a time bin lasting 0.5 ms. For recording the images and spectra, the QDs were excited in the diffraction limited focus of an RPM with a wavelength of 488 nm and power of 1 μW. The intensity trajectory together with a zoom-in of one second show intensity jumps between a maximum level at about 160 counts/0.5 ms and a minimum intensity level at about 5 counts/0.5 ms, which is the background signal. These levels occur as maxima in the distributions plotted on the right of the respective time trace. An intermediate intensity level at 80 counts/0.5 ms can also be observed for some time periods. The longest dark intervals last up to about one second, while the shortest ones that can be resolved here are on the order of 1 ms. Even faster blinking behavior may be hidden in the time traces due to the time binning of 0.5 ms. The observed on–off blinking behavior is a strong argument that only one QD is active in this hybrid system.

Fig. 9 Intensity trajectory of a single CdSe/ZnS-QD bound to the tip of a gold nanocone with a zoom-in of one second. The histograms on the right show how often the PL signal reaches a certain intensity value.

In some cases, not shown here, we also observed repeated jumping between the background and two or even three intensity levels. This behavior could either be explained by two or three closely spaced QDs per tip, or by one single QD that can emit from several levels with different intrinsic emission quantum efficiencies Φ(t).⁶³

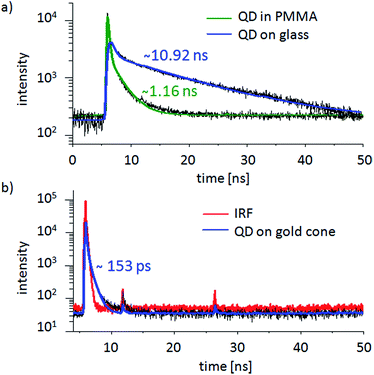
To further investigate the influence of plasmon modes on the excited state of single QDs, we also performed fluorescence lifetime measurements. A pulsed supercontinuum laser (SuperK Extreme EXB-4, NKT Photonics, Denmark) operating at a repetition rate of 20 MHz was used as an excitation source. Using an acousto-optical tunable filter (AOTF, SuperK Select, NKT Photonics, Denmark), a laser wavelength of 488 nm was chosen in combination with a time-correlated single photon counting system (Picoquant, Berlin, Germany) with a spectrally integrating detector (PDM series, Micro Photon Devices, Italy) providing a nominal timing resolution <50 ps. The lifetime histograms were integrated until a reasonable intensity for the following fitting procedures (at least 10³ counts for the peak channel) was collected. The raw data were fitted with a bi-exponential decay function convoluted with the instrument response function (IRF) and the intensity-weighted average fluorescence lifetime values were calculated according to:

Fig. 10 shows typical fluorescence decay curves of QDs in different environments. The lifetime of an isolated CdSe/ZnS-QD on a glass cover slide can be described as a bi-exponential decay with an average lifetime on the order of 10 ns. In PMMA we observe a fluorescence lifetime around 1.6 ns and a multi-exponential decay, as has also been observed in other polymers.⁶³ Both values are in good agreement with the literature.^64,65 In contrast, the QD bound to the gold nanocone shows a significantly shorter lifetime. The measured 153 ps is close to the duration of the IRF and reflects an upper limit.

Fig. 10 Original decay data is presented in black. (a) PL intensity decay curves of two isolated single CdSe/ZnS-QDs deposited on a glass cover slide with a fluorescence lifetime of about 10.9 ns (blue) and one in PMMA with a fluorescence lifetime of about 1.16 ns (green). (b) For a QD chemically bound to the tip of a gold cone (blue), the decay is almost as short as the IRF (red) with a calculated lifetime of about 150 ps. The peaks at 11.8 ns and 26.4 ns originate from reflections of the excitation pulse in the optical system, which can arise in certain setup arrangements but only rarely interfere with the fitting procedures.

IV. Conclusions

Gold nanocones with a tunable plasmon resonance present an interesting and promising model for the analysis of optical processes in hybrid structures. The use of a hybrid system of QDs on a conical antenna may lead to an improved understanding of the interaction between QDs and plasmonic nanostructures, and the influence on the QD's emission. The gold cones were designed in such a way that they have a longitudinal plasmon resonance at the PL maximum of the QD. For excitation we used 488 nm radiation, which is off-resonance with the longitudinal mode of the gold cones. By comparing the PL spectra of 51 hybrid systems of QDs indicating single QD behavior, each on top of a conical gold antenna, we observe a red-shift of about 10 nm and in addition a PL intensity on average five times higher than for 78 single QDs of the same batch deposited on glass cover slides. The presence of single QDs was verified by recording intensity trajectories showing distinct on/off blinking. The dark intervals last from one millisecond, as limited by our detection electronics, to about one second. Our results indicate that the luminescence of single QDs and their decay rates can be enhanced by directly binding them to the tips of plasmonic nanocones. The current manuscript reflects work in progress. Further experiments, particularly concerning fluorescence lifetimes, fluorescence intermittency and emission polarization, will be performed.

Acknowledgements

We would like to thank E. Nadler for taking the SEM images of the gold cones. This work was performed in the context of the European COST Action MP1302 Nanospectroscopy. A. J. M. acknowledges partial financial support from DFG project ME 1600/5-3. Support by the Carl Zeiss Foundation is gratefully acknowledged by J. F.

References

1. J. M. Gerton, L. A. Wade, G. A. Lessard, Z. Ma and S. R. Quake, Phys. Rev. Lett., 2004, 93, 180801.
2. E. Shafran, B. D. Mangum and J. M. Gerton, Phys. Rev. Lett., 2011, 107, 037403.
3. A. Hartschuh, H. H. Qian, A. J. Meixner, N. Anderson and L. Novotny, Nano Lett., 2005, 5, 2310–2313.
4. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
5. S. Kuhn, U. Hakanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402.
6. E. B. Urena, M. P. Kreuzer, S. Itzhakov, H. Rigneault, R. Quidant, D. Oron and J. Wenger, Adv. Mater., 2012, 24, OP314–OP320.
7. A. G. Curto, G. Volpe, T. H. Taminiau, M. P. Kreuzer, R. Quidant and N. F. van Hulst, Science, 2010, 329, 930–933.
8. A. Kinkhabwala, Z. F. Yu, S. H. Fan, Y. Avlasevich, K. Mullen and W. E. Moerner, Nat. Photonics, 2009, 3, 654–657.
9. K. Hennessy, A. Badolato, P. M. Petroff and E. Hu, Photonics and Nanostructures, 2004, 2, 65–72.
10. C. J. Wang, L. Huang, B. A. Parviz and L. Y. Lin, Nano Lett., 2006, 6, 2549–2553.
11. D. L. Huffaker, G. Park, Z. Zou, O. B. Shchekin and D. G. Deppe, Appl. Phys. Lett., 1998, 73, 2564–2566.
12. I. Fushman, D. Englund, A. Faraon, N. Stoltz, P. Petroff and J. Vuckovic, Science, 2008, 320, 769–772.
13. A. Mohammadi, V. Sandoghdar and M. Agio, New J. Phys., 2008, 10, 105015.
14. A. M. Kern, A. J. Meixner and O. J. F. Martin, ACS Nano, 2012, 6, 9828–9836.
15. N. Engheta, Science, 2007, 317, 1698–1702.
16. P. Viste, J. Plain, R. Jaffiol, A. Vial, P. M. Adam and P. Royer, ACS Nano, 2010, 4, 759–764.
17. J. Do, R. Schreiber, A. A. Lutich, T. Liedl, J. Rodriguez-Fernandez and J. Feldmann, Nano Lett., 2012, 12, 5008–5013.
18. J. C. Garno, Y. Yang, N. A. Amro, S. Cruchon-Dupeyrat, S. Chen and G.-Y. Liu, Nano Lett., 2003, 3, 389–395.
19. T. van der Sar, E. C. Heeres, G. M. Dmochowski, G. de Lange, L. Robledo, T. H. Oosterkamp and R. Hanson, Appl. Phys. Lett., 2009, 94, 173104.
20. A. W. Schell, G. Kewes, T. Schröder, J. Wolters, T. Aichele and O. Benson, Rev. Sci. Instrum., 2011, 82, 073709.
21. J. Fulmes, R. Jäger, C. Schäfer, S. Jäger, D. A. Gollmer, A. Horrer, E. Nadler, D. Zhang, T. Chassé, A. J. Meixner, D. P. Kern and M. Fleischer, Nanoscale, 2015, 14691–14696.
22. D. Bera, L. Qian, T. K. Tseng and P. H. Holloway, Materials, 2010, 3, 2260–2345.
23. C. T. Yuan, P. Yu, H. C. Ko, J. Huang and J. Tang, ACS Nano, 2009, 3, 3051–3056.
24. A. Hatef, S. M. Sadeghi, E. Boulais and M. Meunier, Nanotechnology, 2013, 24, 015502.
25. A. Horrer, C. Schäfer, K. Broch, D. A. Gollmer, J. Rogalski, J. Fulmes, D. Zhang, A. J. Meixner, F. Schreiber, D. P. Kern and M. Fleischer, Small, 2013, 9, 3987–3992.
26. A. Mooradian, Phys. Rev. Lett., 1969, 22, 185–187.
27. M. R. Beversluis, A. Bouhelier and L. Novotny, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 115433.
28. G. T. Boyd, Z. H. Yu and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7923–7936.
29. A. Tcherniak, S. Dominguez-Medina, W. S. Chang, P. Swanglap, L. S. Slaughter, C. F. Landes and S. Link, J. Phys. Chem. C, 2011, 115, 15938–15949.
30. M. Yorulmaz, S. Khatua, P. Zijlstra, A. Gaiduk and M. Orrit, Nano Lett., 2012, 12, 4385–4391.
31. H. Hu, H. Duan, J. K. Yang and Z. X. Shen, ACS Nano, 2012, 6, 10147–10155.
32. E. Dulkeith, T. Niedereichholz, T. A. Klar, J. Feldmann, G. von Plessen, D. I. Gittins, K. S. Mayya and F. Caruso, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205424.
33. M. B. Mohamed, V. Volkov, S. Link and M. A. El-Sayed, Chem. Phys. Lett., 2000, 317, 517–523.
34. E. Kretschmann, Z. Physik, 1971, 241, 313–324.
35. H. Raether, Surface Plasmons on Smooth and Rough Surfaces and on Gratings, Springer Verlag, 1988.
36. C. Schafer, D. A. Gollmer, A. Horrer, J. Fulmes, A. Weber-Bargioni, S. Cabrini, P. J. Schuck, D. P. Kern and M. Fleischer, Nanoscale, 2013, 5, 7861–7866.
37. J. N. Farahani, D. W. Pohl, H. J. Eisler and B. Hecht, Phys. Rev. Lett., 2005, 95, 017402.
38. C. D. Geddes and J. R. Lakowicz, J. Fluoresc., 2002, 12, 121–129.
39. L. Novotny and B. Hecht, Principles of nano-optics, Cambridge University Press, Cambridge, New York, second edn, 2012.
40. A. M. Kern, D. Zhang, M. Brecht, A. I. Chizhik, A. V. Failla, F. Wackenhut and A. J. Meixner, Chem. Soc. Rev., 2014, 43, 1263–1286.
41. R. X. Bian, R. C. Dunn, X. S. Xie and P. T. Leung, Phys. Rev. Lett., 1995, 75, 4772–4775.
42. H. Fredriksson, Y. Alaverdyan, A. Dmitriev, C. Langhammer, D. S. Sutherland, M. Zaech and B. Kasemo, Adv. Mater., 2007, 19, 4297–4302.
43. M. Fleischer, F. Stade, A. Heeren, M. Haffner, K. Braun, C. Stanciu, R. Ehlich, J. K. H. Horber, A. J. Meixner and D. P. Kern, Microelectron. Eng., 2009, 86, 1219–1221.
44. M. Fleischer, D. Zhang, K. Braun, S. Jager, R. Ehlich, M. Haffner, C. Stanciu, J. K. H. Horber, A. J. Meixner and D. P. Kern, Nanotechnology, 2010, 21, 065301.
45. A. G. Curto, T. H. Taminiau, G. Volpe, M. P. Kreuzer, R. Quidant and N. F. van Hulst, Nat. Commun., 2013, 4, 1750.
46. J. H. Song, T. Atay, S. F. Shi, H. Urabe and A. V. Nurmikko, Nano Lett., 2005, 5, 1557–1561.
47. F. Wackenhut, A. V. Failla, T. Züchner, M. Steiner and A. J. Meixner, Appl. Phys. Lett., 2012, 100, 263102.
48. T. Zuchner, A. V. Failla and A. J. Meixner, Angew. Chem., Int. Ed., 2011, 50, 5274–5293.
49. T. C. Isabell, P. E. Fischione, C. O'Keefe, M. U. Guruz and V. P. Dravid, Microsc. Microanal., 1999, 5, 126–135.
50. M. Antognozzi, A. Sentimenti and U. Valdre, Microsc., Microanal., Microstruct., 1997, 8, 355–368.
51. I. Campillo, J. M. Pitarke, A. Rubio, E. Zarate and P. M. Echenique, Phys. Rev. Lett., 1999, 83, 2230–2233.
52. J. Cao, Y. Gao, H. E. Elsayed-Ali, R. J. D. Miller and D. A. Mantell, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10948–10952.
53. T. V. Shahbazyan, Nano Lett., 2013, 13, 194–198.
54. S. Jäger, Dissertation, Tübingen, 2014.
55. A. I. Chizhik, A. M. Chizhik, D. Khoptyar, S. Bär and A. J. Meixner, Nano Lett., 2011, 11, 1131–1135.
56. J. Kim, J. Lee and K. Kyhm, Appl. Phys. Lett., 2011, 99, 213112.
57. Y. Ito, K. Matsuda and Y. Kanemitsu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 033309.
58. K. E. Knowles, E. A. McArthur and E. A. Weiss, ACS Nano, 2011, 5, 2026–2035.
59. K. Sahu, H. Wu and M. A. Berg, J. Phys. Chem. B, 2013, 117, 15257–15271.
60. R. Schmidt, C. Krasselt, C. Gohler and C. von Borczyskowski, ACS Nano, 2014, 8, 3506–3521.
61. A. A. Cordones and S. R. Leone, Chem. Soc. Rev., 2013, 42, 3209–3221.
62. M. Califano and F. M. Gómez-Campos, Nano Lett., 2013, 13, 2047–2052.
63. G. Schlegel, J. Bohnenberger, I. Potapova and A. Mews, Phys. Rev. Lett., 2002, 88, 137401.
64. W. G. J. H. M. van Sark, P. L. T. M. Frederix, A. A. Bol, H. C. Gerritsen and A. Meijerink, ChemPhysChem, 2002, 3, 871–879.
65. L. Zhu, S. Samudrala, N. Stelmakh and M. Vasilyev, Opt. Express, 2012, 20, 3144–3151.

---