Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultra-strong coupling of molecular materials: spectroscopy and dynamics
Jino
George
,
Shaojun
Wang
,
Thibault
Chervy
,
Antoine
Canaguier-Durand
,
Gael
Schaeffer
,
Jean-Marie
Lehn
,
James A.
Hutchison
*,
Cyriaque
Genet
and
Thomas W.
Ebbesen
*
ISIS & icFRC, Université de Strasbourg & CNRS, 8 allée Gaspard Monge, 67000, Strasbourg, France. E-mail: hutchison@unistra.fr; ebbesen@unistra.fr
First published on 26th February 2015
Abstract
We report here a study of light–matter strong coupling involving three molecules with very different photo-physical properties. In particular we analyze their emission properties and show that the excitation spectra are very different from the static absorption of the coupled systems. Furthermore we report the emission quantum yields and excited state lifetimes, which are self-consistent. The above results raise a number of fundamental questions that are discussed and these demonstrate the need for further experiments and theoretical studies.
1. Introduction
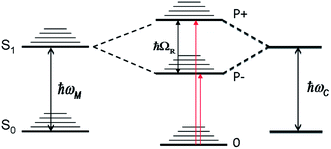
One of the advantages of surface plasmon polaritons is their ability to concentrate the electromagnetic field in a very small volume, which in turn can enhance various phenomena and notably light–matter interactions. Therefore it is not surprising that plasmonic structures and micro-cavities have been used interchangeably to provide confined EM fields to induce light–matter strong coupling in molecular materials. Metallic cavities provide some of the strongest field confinements and have the additional feature that both the Fabry–Perot and plasmonic waveguide modes are present.1,2 When molecular materials are placed in a high concentration in such confined fields, hybrid light–matter states, the so-called polaritonic states P+ and P−, are formed with Rabi splittings in the range of 0.1 to 1 eV, as illustrated in Fig. 1. When the Rabi splitting is a fraction of the transition energy (ℏωM), the perturbation of the coupled system is so strong that the energies of the other states of the system are modified. This is the so-called ultra-strong coupling regime where the ground state energy has been predicted to shift3 and this has indeed been observed experimentally.4,5 In addition, the hybrid light–matter eigen states are in principle delocalized over the optical mode and, upon excitation, quasi-bosonic exciton–polaritons are formed.Such features of a strongly coupled system are quite unique and therefore have naturally generated much research activity from single atom–single photon studies to coupling in inorganic semiconductors and organic dyes.6–18
While early studies on organic materials focused on the J-aggregates of cyanine dyes,18–32 due to their sharp and intense absorption peak, a greater variety of molecules are currently being investigated under strong coupling, depending on the scientific targets.33–44 For instance, the composite bosonic nature of exciton–polaritons makes them of great interest for thresholdless lasing and other collective effects such as Bose–Einstein condensation. However, such reports remain elusive, being demonstrated only for a system incorporating an anthracene single crystal,33 and more recently for fluorinated ladder polymers.34,35 We have been more interested in how the molecular material properties of the coupled system can be modified relative to the bare molecules. Therefore we have chosen other molecules with specific functionalities, such as merocyanine, which is capable of (photo-)switching between two isomers, to demonstrate the effect of those functionalities on chemical reaction rates, work function, phase transitions, and electronic transport.41–45 The observation of such effects belies the notion that only a very small percentage of molecules are coupled for each class of molecules. In fact, the stronger the Rabi splitting, the larger the fraction of coupled molecules.5
Molecular materials are typically highly disordered and inhomogeneously broadened and this has consequences on the strong coupling, both on the properties of the polaritonic states and on the whole system, as pointed out by Michetti and La Rocca.16 In particular, the degree of delocalization of the polaritonic states inside a cavity, together with the fraction of coupled molecules, can be significantly affected. In addition, organic molecules used in strong coupling have typically 100 to 200 normal vibrational modes that also have strong consequences on their properties.32,46,47
With vacuum Rabi splittings (ℏΩRV) in the order of 1 eV, importantly, the coupled system is no longer in the Markovian regime since ℏΩRV ≫ kBT.47 As a consequence, the lifetimes of the polaritonic states P+ and P− cannot be predicted from the lifetimes of the constituents of the system, namely the lifetime of the photon in the cavity and lifetime of the excited state. As we have pointed out elsewhere,32 there are numerous examples of coupled systems that are longer lived than their constituents, for instance in the case of molecular excimers and exciplexes.
A large ℏΩRV can be obtained by using a molecular transition with high absorption cross-sections or transition dipole moments (d) and metallic cavities with small mode volumes (v) since, in the absence of dissipation, the Rabi splitting energy (ℏΩR) between the two new hybrid light–matter states is given by:6
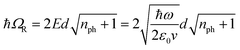 | (1) |
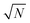 , which implies that the ℏΩRV is proportional to the square root of the molecular concentration (
, which implies that the ℏΩRV is proportional to the square root of the molecular concentration (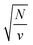 ) in the optical field.
) in the optical field.
Crucial for all these studies is a better understanding of the properties of the polaritonic states (e.g.Fig. 1), their dynamics and how they are modified relative to the bare molecules. A greater variety of molecules need to be characterized to look for trends. We have undertaken such a study and, in this report, the photophysical properties of a subset of strongly coupled molecules with very different bare features are compared using both static and fs time-resolved pump–probe spectroscopy. The results raise fundamental questions that will be discussed.
In this paper the three different molecules that were investigated under strong coupling are as follows:
1.1 TDBC
The first one is the well-known 1,1′-diethyl-3,3′-bis(4-sulfobutyl)-5,5′,6,6′-tetrachlorobenzimidazolocarbocyanine (TDBC) in its J-aggregated form. J-aggregates are themselves formed by transition dipole–dipole strong coupling of neighboring molecules, where the symmetry of the aggregates is such that only the transition from the ground state to the lower coupled state is allowed, as illustrated in Fig. 2b. The Stoke shift is characteristically very small (<10 meV).The Rabi splitting is such that P− lies below the Frenkel excitonic state involved in the coupling process (Fig. 2a). As a consequence, the energy level of the lower polariton branch lies amongst the higher vibrational states of the ground state manifold.47 Thus, even if the polariton state is formed efficiently, it will relax very efficiently by dissipating energy into this bath of non-radiative states. This is despite the fact that polaritons, generated by excitation to P− or P+, are expected to interact (scatter) very weakly with phonons due to their low effective mass (being quasi-bosons). Recent measurements on TDBC (having ∼180 normal vibration modes) show, indeed, that the non-radiative decay rate constant kP−nr of P− is smaller than the corresponding knr of the bare molecule.32 Nevertheless, in both cases the non-radiative rate constants are in the order of 1012 s−1. This dominates the decay kinetics of P−. It is also the source of the low P− fluorescence quantum yield, 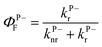 , since the radiative rate constant kP−r has an upper limit for a fully allowed transition in the order of 109 ∼ 1010 s−1. Vibrational relaxation within the excited states occurs on the 100 fs timescale and is characterized by small spectral shifts or sliding during the relaxation. This has also been seen for the P− of TDBC and it is important that this is not confused with other possible excited decay pathways when observing P− and P+ at very short time scales.30
, since the radiative rate constant kP−r has an upper limit for a fully allowed transition in the order of 109 ∼ 1010 s−1. Vibrational relaxation within the excited states occurs on the 100 fs timescale and is characterized by small spectral shifts or sliding during the relaxation. This has also been seen for the P− of TDBC and it is important that this is not confused with other possible excited decay pathways when observing P− and P+ at very short time scales.30
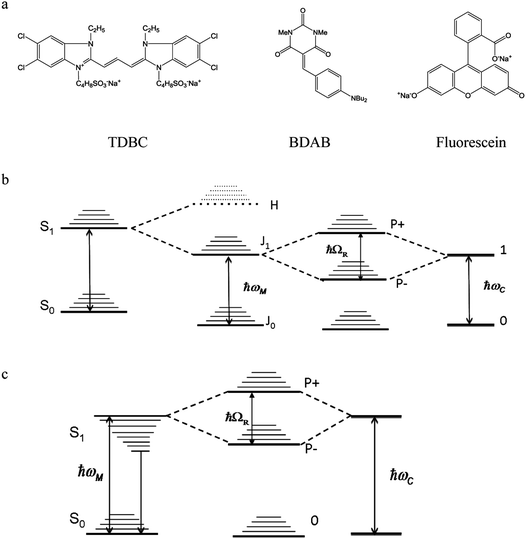 | ||
| Fig. 2 Molecular structures of the three compounds (a) and the corresponding energy diagrams for TDBC (b) and BDAB (c) upon coupling. The TDBC dipole–dipole coupling gives rise to new states marked J and H, but for the J-aggregates only the J state is observed in the absorption spectrum as the transition to H is forbidden. Fluorescein is coupled schematically as in Fig. 1. | ||
1.2 BDAB
The second molecule is a so-called push–pull molecule, 5-(4-(dibutylamino)benzylidene)-1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione (BDAB),5 with an unusually large Stokes shift (∼560 meV). The strong coupling energy level diagram for such molecular systems that undergo electronic energy re-distribution in the excited state, with the associated solvation shell re-distribution, i.e. systems featuring a large Stoke shift, is shown in Fig. 2c. The strong coupling in this case involves the transition from the molecular ground state to a higher vibrational state of the excited state manifold (the Franck–Condon transition). As a consequence, the lower P− polariton branch may lie above, or be isoenergetic with, the relaxed excited state of the bare molecule (see for instance ref. 37). This may have consequences on the dynamics and the decay processes of the coupled system, as has already been shown by Törmä and co-workers.371.3 Fluorescein
Fluorescein, as its name indicates, is a highly fluorescent dye in dilute solutions with a ΦF ≃ 0.9 and a Stoke shift of ∼110 meV. It is a representative of standard organic dyes and will strongly couple to the cavity, as illustrated in Fig. 1.2. Results
The strongly coupled samples were prepared by encasing polymer films containing the dyes between two silver films to form an optical cavity (see Experimental section for details). The thickness of the polymer film, and thus the final separation between the Ag mirrors in the cavity, was chosen to give an optical mode resonant with the absorption maximum of the dye/aggregate (at 590 nm for TDBC, 470 nm for BDAB, and 510 nm for fluorescein). The Q-factors of these cavities are low, typically ∼10–20. Unless specified otherwise, the cavity thicknesses are tuned such that the Rabi splitting occurs at normal incidence (k// = 0) where the photon–exciton mixing is 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50.
50.
2.1 Transition probability to P−
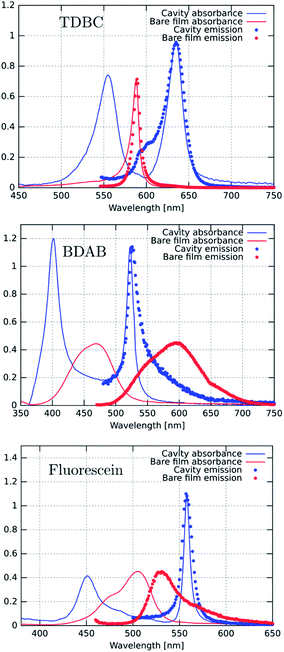
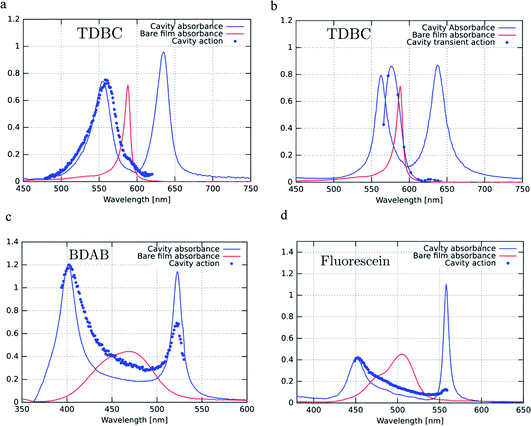
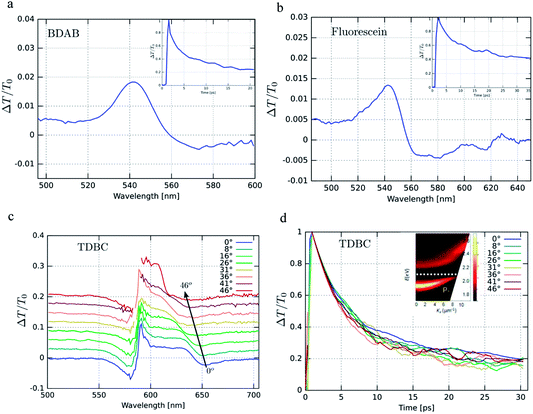
We start by comparing in Fig. 3a–c the optical absorption and emission (fluorescence) spectra of the Fabry–Perot cavities containing TDBC, fluorescein and BDAB at normal incidence with their bare spectra. All the absorption spectra are inhomogeneously broadened, even TDBC. The two new absorption peaks corresponding to P+ and P− (blue solid curves in Fig. 3) have a full width half maximum (FWHM) that is mainly determined by that of the cavity mode, as expected.14 It should be noted that for fluorescein the cavity induced splitting is more complex, due to the double peaked absorption of the bare molecule, as seen before for Rhodamine.37 The coupling strengths (ℏΩRV) for these samples are, respectively, 277, 554 and 720 meV for TDBC, BDAB and fluorescein and the corresponding fractions of the transition energy (ℏΩRV/ℏω0) are 13, 24 and 27%. These fractions, especially the latter two, are sufficiently high that the coupled systems are in the ultra-strong coupling regime, which has consequences on their properties as already discussed. Notice that the P− fluorescence peak of coupled BDAB is at higher energy than that of the bare molecule in agreement with the schematic illustration of Fig. 2c. Careful observation of the emission spectra of the coupled systems shows that at least some fluorescence of the bare molecules is always present in these cavities. In other words, some of the molecules are not coupled to the cavity due to the disorder (energetic and orientational) in the system.5,16 This uncoupled emission does not disperse with angle and therefore can be easily distinguished from the P− emission. The apparent Stoke shift of the P− emission for all three molecules is extremely small or, depending on the conditions of the sample, it sometimes even appears to be slightly blue shifted relative to absorption.30 The blue shifted emission and its origin will be discussed again further on, after the presentation of more results.Next, we measured the excitation spectra or action spectra associated with the P− emission. This is a standard technique used in molecular science to understand the origin of the emission and associated processes and we first introduced this for studying strong coupling in an earlier study.30 It consists of measuring the emission or fluorescence intensity, IF(λ), at a given wavelength while scanning the excitation wavelength through the absorption spectrum of the sample. Since IF(λ) ∝ ΦFσA(λ)I0(λ)c = ΦFIA(λ), where σA(λ) is the absorption cross section of the molecule, c is the molecular concentration and I0(λ) is the incident light intensity, one would expect that when I0 is normalized then IF(λ) will be proportional to the light absorbed, IA(λ). Therefore, by just plotting IF at a given λ while scanning the normalized excitation, I0(λ), the shape obtained should reflect the absorbance of the states contributing to the emission process.
Fig. 4a, c and d show the excitation spectra of the three molecules recorded for their P− emission and these are compared to their absorbance spectra. The first striking feature is the relative contribution of P+ and P− to the emission of P− (here all the excitation spectra have been normalized to the P+ absorbance peak). It thus appears that the direct excitation of the P− peak contributes very little to the P− emission, while when exciting to P+ or the uncoupled molecules it rapidly relaxes to P−, where emission can occur. This relaxation to P− can occur via energy transfer between the coupled and the uncoupled molecular reservoirs as well as by rapid internal vibrational relaxation (IVR). The latter is a standard feature of molecules, with their very large number of normal modes and their overtones that provide a continuum of sublevels between the various states. It is interesting to note that the ratio of P−/P+ excitation peaks is the smallest for TDBC (∼0.1) and the largest for BDAB (∼0.5).
This raises the question of whether the direct excitation into the P− static absorption peak actually populates P− or not. To answer this question we also recorded the excitation spectrum of pump–probe experiments by looking at the intensity of the transient absorption spectrum of P−, proportional to the population of P−, as a function of laser pump wavelength. This was possible to do for TDBC since our 150 fs-laser could be tuned to cover the static absorption peaks. The resulting spectrum is plotted in Fig. 4b and it has very similar features to the fluorescence excitation spectrum (Fig. 4a). Again, the direct excitation of P− appears not to be allowed. Interestingly, the ℏΩRV deduced from the excitation spectra appears to be smaller than the static absorption spectrum indicates. This is probably the origin of the blue-shifted emission relative to the static absorption that is sometimes observed.
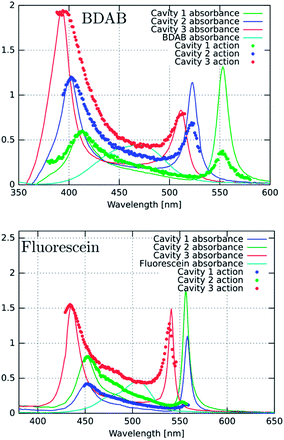
To try to understand the origin of these observations, the cavities were detuned and the fluorescence excitation spectra were recorded. For fluorescein, the detuning of the cavity to higher energies (ca. 60 meV) seems to enhance direct P− excitation, as shown in Fig. 5a (red curve). This could be explained by the higher exciton content of the P− branch. However, in the case of BDAB (Fig. 5b), the reverse tendency is seen, i.e. detuning to lower energies enhances the relative contribution of P− to the excitation spectrum. Taken together with the results of Fig. 4, it appears that the internal vibronic structure of the molecule plays an important role and also possibly the excited state rearrangement involved in the Stoke shift.
2.2 Lifetime of P−
The transient spectra of the three strongly coupled systems are shown in Fig. 6, together with their decay kinetics. The spectra do not evolve over the decay, indicating that they are dominated by a single transient species. The decays are not single exponentials due to the heterogeneities of the samples at the high concentrations that were used to induce strong coupling. The angle dependence of the decay was also measured for TDBC and was found to be invariant, indicating that the lifetime is not dependent on probed k-vector. This indicates that there is no bottle-neck along the P− branch shown in Fig. 6 for this sample. Such decay bottle-necks have been seen in other conditions and samples for strongly coupled TDBC.24Table 1 below summarizes the dynamical data for the strongly coupled molecules. It first compares the observed half-lives measured by transient absorption with those of the 1/linewidth of the P− resonance and the experimental radiative lifetimes, as well as the predicted ones derived from absorbance peaks of P− using the Bowen and Wokes approximation.48 It is notable that these two standard methods for estimating lifetimes give such very different values. The measured and calculated quantum yields for TDBC and fluorescein are in very good agreement, considering all the experimental uncertainty, while for BDAB the experimental value is an order of magnitude higher. The latter is not surprising considering the fact that the emission is not from the Franck–Condon transition but due instead to an intra-molecular charge transfer state being at the origin of the large Stoke shift of the bare molecule. Thus, the Bowen and Wokes approximation is not the best model for such a molecule.
| TBDC | BDAB | Fluorescein | |
|---|---|---|---|
| 1st half life (transient absorption) | 4.3 ps | 3.5 ps | 30 ps |
| Cavity lifetime (1/linewidth) | 2 fs | 5 fs | 14 fs |
| Radiative lifetime (predicted value) | 0.2 ns (0.4 ns) | 1 ns (0.1 ns) | 3 ns (1.5 ns) |
| Quantum yield (predicted value) | 1 × 10−2 (2 × 10−2) | 4 × 10−2 (3.5 × 10−3) | 2 × 10−2 (1 × 10−2) |
3. Discussion and conclusions
Conspicuous from the above excitation spectral experiments is the fact that the static absorption peak due to P− (in Fig. 3–5) does not readily lead to the generation of P− emission or even to the P− transient absorption. We have shown this excitation behaviour before for TDBC and it has since been confirmed by others.24 This finding is surprising since one would expect that the static absorption peak of P− would lead directly to populating P− and subsequent emission. This is an important issue since it is a standard assumption that the emission in the spectral region of P− indeed comes from a corresponding state.One could take a very naïve view to explain the above results from a purely classical interpretation. For instance, the shape of P− emission spectra can be very easily reproduced by taking the emission of the bare molecules filtered by the transmission properties of the cavity (as can be seen in Fig. 3). The excitation spectrum would therefore be dominated by the spectral regions where the bare molecule absorbs but enhanced by the modal properties of the cavity (as in Fig. 4). This is similar to the treatment of strong coupling by Zhu et al. where it is not necessary to assume the formation of hybrid light–matter states by vacuum Rabi splitting.11 In this classical vision, the lifetimes of the P− measured by fluorescence or by transient absorption spectroscopy would be those of the bare molecule perturbed by the strong interaction with the confined electromagnetic environment of the cavity.
Nevertheless, the observation of novel and modified properties in strongly coupled systems argues strongly for the quantum interpretation and the existence of hybrid light–matter states. These include coherent emission over large distances,23 condensation of polariton,34,35 polariton lasing33 and modification of such properties as chemical rates,42 work-function43 and conductivity,45 amongst others. The significant P− emission quantum yields also argue against a simple cavity filter effect for the fluorescence. Therefore there is a need to understand why the direct excitation of P− is a very inefficient way of populating the state, despite the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 photonic–exciton mixing for both P+ and P− in our experiments.
50 photonic–exciton mixing for both P+ and P− in our experiments.
One possibility is that the transition probability is very weak despite the strong static absorption. This immediately raises the question of what is at the origin of the static absorption. One unique characteristic of these organic coupled systems is the large inhomogeneous broadening which, coupled to the cavity, could generate dissipation without populating P−. This would leave indirect excitation via higher energy states involving energy transfer and IVR as the most efficient means of then populating the P− state. However, as we discussed previously,32 the recorded P− emission quantum efficiencies are only compatible with a lifetime in the picosecond regime, as measured for P− both in fluorescence and transient absorption. It is important to note that this is for a most favourable kr corresponding to a highly allowed transition. If the transition to P− is only weakly allowed, then ΦP−F should be much smaller, unless the strongly coupled system boosts the emission for an otherwise weakly allowed transition.
Another conundrum for us in these systems is also related to lifetimes. From the FWHM of the P− and P+ absorption, principally determined by the Q-factor of the cavity,14 one derives a lifetime of ∼10 fs. If one integrates over the same absorbance peak to derive the radiative lifetime, one obtains a lifetime three orders of magnitude longer.32 These represent two very different approaches, one optical and one molecular, to the same issue.
In the spirit of the Faraday discussions, we have shown here, through experiments, some of the open questions related to light–matter strong coupling involving molecular materials. Clearly more experiments and theory that can handle such complex materials and the particularities associated with individual molecular structures need to be developed to elucidate these strongly interacting systems. Only then will the full potential of using a confined electromagnetic environment to control material and molecular properties be realized.
4. Experimental
All the steady state measurements were performed in reflective cavities, in which the Ag mirror deposited on the glass was 200 nm thick, and the top mirror was 30 nm thick. For pump–probe measurements, experiments were performed in transmission with cavities in which both mirrors were 30 nm thick. The bottom Ag film was sputtered on borosilicate glass, followed by spin-coating of the molecules dispersed in a polymer to form a thin film, and then sputtering the second Ag film on top. TDBC films were spin-cast from aqueous solution (Milli-Q) containing 0.5% TDBC and 5% poly(vinyl) alcohol (PVA, M.W. 205![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) by weight. Fluorescein films were cast from aqueous solutions of 1% Fluorescein disodium salt and 2% PVA by weight. BDAB films were cast from toluene solutions of 0.5% BDAB and 1% poly(methyl methacrylate) (PMMA, M.W. 120
000) by weight. Fluorescein films were cast from aqueous solutions of 1% Fluorescein disodium salt and 2% PVA by weight. BDAB films were cast from toluene solutions of 0.5% BDAB and 1% poly(methyl methacrylate) (PMMA, M.W. 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) by weight. Toluene (Sigma Aldrich), PVA (FLUKA), PMMA (Sigma Aldrich), fluorescein disodium salt (Exciton) and TDBC (Few Chemicals) were obtained commercially and used without further purification. BDAB, 5-(4-(dibutylamino)benzylidene)-1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione, was synthesized as follows. 4-dibutylaminobenzaldehyde (196 mg, 840 μmol, 1.00 eq.) and 1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione (131 mg, 840 μmol, 1.00 eq.) were dissolved in 5 mL of ethanol. The resulting mixture was refluxed for 3 h. After cooling the precipitate was filtered off and washed with 10 mL of H2O, 10 mL of ethanol and 10 mL of n-pentane. The yellow solid was dried in vacuum to give the product in quantitative yield (312 mg). 1H NMR (400 MHz, CDCl3, δ/ppm): 0.98 (t, J = 7.3 Hz, 6H), 1.45–1.32 (m, 4H), 1.69–1.57 (m, 4H), 3.44–3.37 (m, 10H), 6.66 (d, J = 8.98 Hz, 2H), 8.36–8.41 (d, J = 9.23 Hz, 3H). ESI-MS: m/z: 360.3 (100%). HRMS (ESI, m/z): calculated for C21H29N3NaO3 394.210; found 394.210.
000) by weight. Toluene (Sigma Aldrich), PVA (FLUKA), PMMA (Sigma Aldrich), fluorescein disodium salt (Exciton) and TDBC (Few Chemicals) were obtained commercially and used without further purification. BDAB, 5-(4-(dibutylamino)benzylidene)-1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione, was synthesized as follows. 4-dibutylaminobenzaldehyde (196 mg, 840 μmol, 1.00 eq.) and 1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione (131 mg, 840 μmol, 1.00 eq.) were dissolved in 5 mL of ethanol. The resulting mixture was refluxed for 3 h. After cooling the precipitate was filtered off and washed with 10 mL of H2O, 10 mL of ethanol and 10 mL of n-pentane. The yellow solid was dried in vacuum to give the product in quantitative yield (312 mg). 1H NMR (400 MHz, CDCl3, δ/ppm): 0.98 (t, J = 7.3 Hz, 6H), 1.45–1.32 (m, 4H), 1.69–1.57 (m, 4H), 3.44–3.37 (m, 10H), 6.66 (d, J = 8.98 Hz, 2H), 8.36–8.41 (d, J = 9.23 Hz, 3H). ESI-MS: m/z: 360.3 (100%). HRMS (ESI, m/z): calculated for C21H29N3NaO3 394.210; found 394.210.
Steady-state transmission and reflection spectra were taken on a Shimadzu UV3101 spectrometer. Steady-state fluorescence spectra were taken with a Horiba Jobin Yvon-Spex Fluorolog-3 fluorimeter. Pump–probe experiments were carried out with narrow band (linewidth = 6 nm), 150 fs-pulse tunable SpectraPhysics laser system. The spectra were recorded using low-energy (<100 μJ cm−2) pumping pulses to avoid spurious effects.
Acknowledgements
The authors acknowledge support from the ERC (Grants 227557), the International Center for Frontier Research in Chemistry (icFRC, Strasbourg), the ANR Equipex “Union” (ANR-10-EQPX-52-01), the Labex NIE projects (ANR-11-LABX-0058_NIE), CSC (ANR-10-LABX-0026_CSC) and USIAS within the Investissement d'Avenir program ANR-10-IDEX-0002-02.References
- S. Kéna-Cohen, S. A. Maier and D. D. C. Bradley, Adv. Opt. Mater., 2013, 1, 827 CrossRef
.
- E. N. Economou, Phys. Rev., 1969, 182, 539 CrossRef
.
- C. Ciuti, G. Bastard and I. Carusotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115303 CrossRef
.
- P. Forn-Díaz, J. Lisenfeld, D. Marcos, J. J. García-Ripoll, E. Solano, C. J. P. M. Harmans and J. E. Mooij, Phys. Rev. Lett., 2010, 105, 237001 CrossRef
.
- A. Canaguier-Durand, E. Devaux, J. George, Y. Pang, J. A. Hutchison, T. Schwartz, C. Genet, N. Wilhelms, J.-M. Lehn and T. W. Ebbesen, Angew. Chem., Int. Ed., 2013, 52, 10533 CrossRef CAS PubMed
.
- S. Haroche and D. Kleppner, Phys. Today, 1989, 42, 24 CrossRef CAS PubMed
.
- R. Houdré, Phys. Status Solidi B, 2005, 242, 2167 CrossRef
.
- P. Snoke and D. Littlewood, Phys. Today, 2010, 63, 42 CrossRef PubMed
.
- Y. Kaluzny, P. Goy, M. Gross, J. M. Raimond and S. Haroche, Phys. Rev. Lett., 1983, 51, 1175 CrossRef CAS
.
- G. Rempe, H. Walther and N. Klein, Phys. Rev. Lett., 1987, 58, 353 CrossRef CAS
.
- Y. Zhu, D. J. Gauthier, S. E. Morin, Q. Wu, H. J. Carmichael and T. W. Mossberg, Phys. Rev. Lett., 1990, 64, 2499 CrossRef CAS
.
- R. J. Thompson, G. Rempe and H. J. Kimble, Phys. Rev. Lett., 1992, 68, 1132 CrossRef CAS
.
- C. Weisbuch, M. Nishioka, A. Ishikawa and Y. Arakawa, Phys. Rev. Lett., 1992, 69, 3314 CrossRef CAS
.
- R. Houdré, R. P. Stanley and M. Ilegems, Phys. Rev. A, 1996, 53, 2711 CrossRef
.
- F. Tassone, C. Piermarocchi, V. Savona, A. Quattropani and P. Schwendimann, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 7554 CrossRef CAS
.
- P. Michetti and G. C. La Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115320 CrossRef
.
- K. G. Lagoudakis, M. Wouters, M. Richard, A. Baas, I. Carusotto, R. Andre, L. E. S. I. Dang and B. Deveaud-Pledran, Nat. Phys., 2008, 4, 706 CrossRef CAS
.
- D. G. Lidzey, D. D. C. Bradley, M. S. Skolnick, T. Virgili, S. Walker and D. M. Whittaker, Nature, 1998, 395, 53 CrossRef CAS PubMed
.
- P. A. Hobson, W. L. Barnes, D. G. Lidzey, G. A. Gehring, D. M. Whittaker, M. S. Skolnick and S. Walker, Appl. Phys. Lett., 2002, 81, 3519 CrossRef CAS PubMed
.
- Y. Sugawara, T. A. Kelf, J. J. Baumberg, M. E Abdelsalam and P. N. Bartlett, Phys. Rev. Lett., 2006, 97, 266808 CrossRef CAS
.
- N. T. Fofang, N. K. Grady, Z. Fan, A. O. Govorov and N. J. Halas, Nano Lett., 2011, 11, 1556 CrossRef CAS PubMed
.
- J. R. Tischler, M. Scott Bradley, Q. Zhang, T. Atay, A. Nurmikko and V. Bulović, Org. Electron., 2007, 8, 94 CrossRef CAS PubMed
.
- S. Aberra Guebrou, C. Symonds, E. Homeyer, J. C. Plenet, Y. N. Gartstein, V. M. Agranovich and J. Bellessa, Phys. Rev. Lett., 2012, 108, 066401 CrossRef
.
- D. M. Coles, R. T. Grant, D. G. Lidzey, C. Clark and P. G. Lagoudakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 121303(R) CrossRef
.
- P. Vasa, W. Wang, R. Pomraenke, M. Lammers, M. Maiuri, C. Manzoni, G. Cerullo and C. Lienau, Nat. Photonics, 2013, 7, 128 CrossRef CAS
.
- G. Zengin, G. Johansson, P. Johansson, T. J. Antosiewicz, M. Käll and T. Shegai, Sci. Rep., 2013, 3, 3074 Search PubMed
.
- Y.-W. Hao, H.-Y. Wang, Y. Jiang, Q.-D. Chen, K. Ueno, W.-Q. Wang, H. Misawa and H.-B. Sun, Angew. Chem., Int. Ed., 2011, 123, 7970 CrossRef
.
- J. Dintinger, S. Klein, F. Bustos, W. L. Barnes and T. W. Ebbesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035424 CrossRef
.
- A. Salomon, C. Genet and T. W. Ebbesen, Angew. Chem., Int. Ed., 2009, 48, 8748 CrossRef CAS PubMed
.
- T. Schwartz, J. A. Hutchison, J. Léonard, C. Genet, S. Haacke and T. W. Ebbesen, ChemPhysChem, 2013, 14, 125 CrossRef CAS PubMed
.
- A. Salomon, S. Wang, J. A. Hutchison, C. Genet and T. W. Ebbesen, ChemPhysChem, 2013, 14, 1882 CrossRef CAS PubMed
.
- S. Wang, T. Chervy, J. George, J. A. Hutchison, C. Genet and T. W. Ebbesen, J. Phys. Chem. Lett., 2014, 5, 1433 CrossRef CAS
.
- S. Kéna-Cohen and S. R. Forrest, Nat. Photonics, 2010, 4, 371 CrossRef
.
- J. D. Plumhof, T. Stoferle, L. J. Mai, U. Scherf and R. F. Mahrt, Nat. Mater., 2014, 13, 248 Search PubMed
.
- K. S. Daskalakis, S. A. Maier, R. Murray and S. Kéna-Cohen, Nat. Mater., 2014, 13, 271 CrossRef CAS PubMed
.
- M. A. Koponen, U. Hohenester, T. K. Hakala and J. J. Toppari, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085425 CrossRef
.
- T. K. Hakala, J. J. Toppari, A. Kuzyk, M. Pettersson, H. Tikkanen, H. Kunttu and P. Törmä, Phys. Rev. Lett., 2009, 103, 053602 CrossRef CAS
.
- W. Ni, Z. Yang, H. Chen, L. Li and J. Wang, J. Am. Chem. Soc., 2008, 130, 6692 CrossRef CAS PubMed
.
- A. Berrier, R. Cools, C. Arnold, P. Offermans, M. Crego-Calama, S. H. Brongersma and J. Gómez-Rivas, ACS Nano, 2011, 5, 6226 CrossRef CAS PubMed
.
- F. Valmorra, M. Bröll, S. Schwaiger, N. Welzel, D. Heitmann and S. Mendach, Appl. Phys. Lett., 2011, 99, 051110 CrossRef PubMed
.
- T. Schwartz, J. A. Hutchison, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2011, 106, 196405 CrossRef CAS
.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592 CrossRef CAS PubMed
.
- J. A. Hutchison, A. Liscio, T. Schwartz, A. Canaguier-Durand, C. Genet, V. Palermo, P. Samorì and T. W. Ebbesen, Adv. Mater., 2013, 25, 2481 CrossRef CAS PubMed
.
- S. J. Wang, A. Mika, J. A. Hutchison, C. Genet, A. Jouaiti, M. W. Hosseini and T. W. Ebbesen, Nanoscale, 2014, 6, 7243 RSC
.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J.-F. Dayen, B. Doudin, F. Stellacci, C. Genet, P. Samorì and T. W. Ebbesen, 2014, arXiv:1409.1900%20[cond-mat.mtrl-sci].
- J. A. Ćwik, S. Reja, P. B. Littlewood and J. Keeling, EPL, 2014, 105, 47009 CrossRef
.
- A. Canaguier-Durand, C. Genet, A. Lambrecht, T. W. Ebbesen and S. Reynaud, 2013, arXiv:1307.8378%20[cond-mat.mes-hall].
-
J. B. Birks, Photophysics of Aromatic Molecules, Wiley-Interscience, 1970 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |