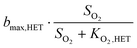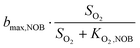Observability of anammox activity in single-stage nitritation/anammox reactors using mass balances†
Sarina
Schielke-Jenni
a,
Kris
Villez
a,
Eberhard
Morgenroth
ab and
Kai M.
Udert
*a
aEawag, Swiss Federal Institute of Aquatic Science and Technology, 8600 Dübendorf, Switzerland. E-mail: kai.udert@eawag.ch; Tel: +41 58 765 53 60
bInstitute of Environmental Engineering, ETH Zurich, 8093 Zurich, Switzerland
First published on 5th June 2015
Abstract
In nitritation/anammox reactors, several bacterial groups contribute to the overall nitrogen conversion. Knowing the activity of the main bacterial groups, especially of anaerobic ammonium-oxidising bacteria (AMX), is extremely helpful to understand the process and optimise its operation. Mass balances of dissolved compounds such as ammonium, nitrite and nitrate commonly allow the determination of bacterial activities in a nitritation/anammox process, but the activity of heterotrophic bacteria (HET) is usually neglected. However, even in wastewater with a low organic substrate content, heterotrophic denitrification can contribute substantially to nitrogen removal. The goal of this study was to critically evaluate the applicability of mass balances for the determination of the relevant bacterial activities in a nitritation/anammox process with high HET activity. We set up and solved mass balances of different degrees of complexity. Both linear equation systems, with catabolic reactions alone and with balances according to the activated sludge model stoichiometry, do not allow estimation of any of the considered bacterial activities. When kinetic rate expressions are included, it is possible to compute the concentrations of all considered bacterial groups, but the estimation uncertainty is far too high for practical purposes: the relative standard deviation for AMX is 5280%. In a completely autotrophic system, the relative standard deviation for AMX is only 5%, which proves that the high standard deviations are due to the complexity of the nitration–anammox process with HET activity. The high standard deviations of the calculated bacterial concentrations can be significantly reduced by adding an additional mass balance for the total biomass (standard deviation for AMX activity 1210%). The required number of measurements to achieve an acceptable precision, in our example about 600 conversion rate measurements to reach a 50% standard deviation for the AMX concentration, is still far too high though for practical purposes. To conclude, mass balances including kinetics theoretically allow the observation of the bacterial activities in nitritation/anammox reactors with high HET activity. However, the required precision of the calculated conversion rates, the uncertainty of stoichiometric and kinetic parameters and the reactor dynamics (unsteady conditions) make mass balances unsuitable for practical estimation of AMX activity. Due to high frequency and new online instruments, mass balances might become a suitable tool in the future.
Water impactThe nitritation/anammox process is an emerging technology for the removal of nitrogen from wastewater with the final goal of preventing eutrophication. To ensure long-term process stability, the activity of the slow-growing anammox bacteria must be known. Mass balances are often used to determine the anammox activity, but heterotrophic activity (e.g. denitrification) is usually neglected in such calculations. This is critical for wastewaters containing considerable amounts of organic substrates (e.g. municipal wastewater in the mainstream or urine). We show that, in theory, mass balances allow the determination of anammox activity also under such conditions, but, in practise, the variance of the calculated rates is too high to be meaningful for plant operation. Alternative methods must be used to determine the anammox activity. |
1. Introduction
Nitrogen removal using the nitritation/anammox process is a cost-efficient alternative to conventional nitrification/denitrification, due to reductions in the requirements for oxygen and organic substrates in comparison to conventional nitrification/denitrification processes. However, maintaining a high activity of anammox bacteria (AMX) can be challenging.1 Especially in reactors with high ratios of biodegradable organic carbon to nitrogen (COD/N), decreasing AMX activity might not be noticed in time, because heterotrophic bacteria (HET) take over a considerable part of the nitrogen removal from AMX.2 Several analytical and experimental methods exist for the reliable determination of AMX concentrations or activities as Podmirseg et al.3 have shown recently. However, all of these methods require instruments which are not available at typical wastewater treatment plants. It would be desirable to be able to calculate the activities of the involved bacterial groups from regularly measured variables for performance monitoring such as the concentrations of, for example, ammonium and nitrite.Mass balances for nitrogen compounds, i.e., ammonium, nitrite and nitrate, have frequently been used to calculate the activities of aerobic ammonium-oxidising bacteria (AOB), nitrite-oxidising bacteria (NOB) and AMX in nitritation/anammox reactors.4,5 However, as elaborated by Mutlu et al.,6 the calculation of AOB, NOB and AMX activity with such mass balances is coupled to the assumption that the activity of HET is negligible. Quite frequently, this assumption is incorrect. On the one hand, it has been shown experimentally that even in biofilm systems without organic carbon in the influent, up to 50% of the biomass can be heterotrophic, supported by microbial decay products.7,8 On the other hand, wastewater almost always contains biodegradable organic matter. Digester supernatant, which is the most common influent for a nitritation/anammox system, has COD/N ratios in the range of 0.2 to 0.5 g COD g N−1.9–11 Some wastewaters even have elevated COD/N ratios in the range of 1 to 1.5 g COD g N−1, which is still not high enough for complete nitrogen removal via heterotrophic denitritation. Examples are stored urine with a theoretical COD/N ratio between 1 g COD g N−1 and 1.5 g COD g N−1.12,13 COD/N ratios of approximately 1 g COD g N−1 are also expected in the recently discussed integration of anammox into mainstream wastewater treatment.14,15
To our knowledge, only three studies included COD consumption in their mass balances to assess the bacterial activities in a nitritation/anammox process.16–18 These three studies used four equations representing the conversion of ammonium, nitrite, nitrate and COD. As only four unknowns can be determined with four independent equations, the authors considered only the activities of AOB, NOB, AMX and nitrate reduction by HET. However, in single-stage nitritation/anammox reactors, heterotrophic consumption of oxygen and nitrite is not negligible. For one thing, the yield of HET growth with oxygen is higher than that with nitrite and nitrate, and therefore, in the presence of all three electron acceptors, HET might prefer oxygen over nitrate and nitrite. Secondly, especially in the presence of high amounts of biodegradable organic matter, HET are able to take over a substantial part of the nitrite removal from AMX.2
The goal of this study is to critically evaluate whether mass balances with commonly measured compounds (for example, ammonium and nitrite) can be used to observe the six main bacterial activities in a single-stage nitritation/anammox reactor: aerobic ammonium oxidation by AOB, nitrite oxidation by NOB, anaerobic ammonium oxidation by AMX, heterotrophic oxygen reduction, heterotrophic nitrite reduction and heterotrophic nitrate reduction. Mass balances with increasing complexity are analysed starting with catabolic reactions only and ending with a stoichiometric matrix which accounts for information on both catabolic and anabolic reactions, microbial kinetic rate functions and a balance for biomass. For all resulting mass balances, both structural and practical observability of the bacterial activities are evaluated.
2. Material and methods
2.1 Definitions
In this paper, we use the following definitions.2.2 Choice of state variables
The considered mass balances involve seven compounds: ammonium (NH4+), nitrite (NO2−), nitrate (NO3−), oxygen (O2), dissolved organic substances (measured as chemical oxygen demand, COD), protons (H+) and total inorganic carbon (TIC). These compounds and their net conversion rates can be determined on large wastewater treatment plants without highly sophisticated analytical methods. Most of these compounds and their conversion rates are directly accessible with measurements: NH4+, NO2−, NO3−, O2, and organic substances. The H+ conversion rate and the concentration and conversion rate of TIC can be calculated from alkalinity measurements, pH values and estimations of the CO2 stripping. It should be noted that in more highly concentrated wastewaters (for example, digester supernatant or urine) additional bases such as phosphate species or free ammonia need to be measured and accounted for. To simplify the mass balance for dissolved biodegradable organic substances, we assume that all organic substances are degraded by bacteria. We choose acetate (C2H3O2−, abbreviated as Ac) to represent the organic compounds.2.3 Determining the net conversion rates
We assumed that measurements are taken from an ideally stirred continuous flow reactor with biomass retention in which all state variables are at their steady-state values. For dissolved compounds, which have no gas phase exchange, the net conversion rate can be calculated as follows: | (1) |
Volatile compounds, such as O2 and CO2, are influenced by gas exchange processes. In this case, the net conversion rate rSi becomes
 | (2) |
 | (3) |
Net conversion rates can also be given for particulate compounds such as bacteria and inert biomass:
 | (4) |
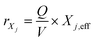 for all bacteria and inert biomass.
for all bacteria and inert biomass.
2.4 Setting up the mass balances
In general, mass balance equations for a system with n compounds and m relevant bacterial reactions (R) result in an equation system with the following structure: | (5) |
Eqn (5) can also be written in matrix notation as
| A·rR = rC | (6) |
2.5 Mass balances with catabolic reactions only (equation system 1)
In the first equation system, we assumed that biomass growth and biomass decay are in equilibrium and no inert biomass is produced; this means the net biomass production is zero. For such a system, the net conversion rates are mainly determined by catabolic bacterial reactions. With this approach, the stoichiometric coefficients are given by the chemical sum formulae of the catabolic reactions and do not require empirically determined parameters such as yield or nitrogen content of biomass.The six main catabolic bacterial reactions in a nitritation/anammox reactor with heterotrophic activity are given as follows.
Heterotrophic COD degradation with O2:
| C2H3O−2 + H+ + 2O2 → 2CO2 + 2H2O | (7) |
Heterotrophic COD degradation with NO−2:
 | (8) |
Heterotrophic COD degradation with NO−3:
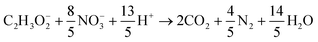 | (9) |
Aerobic ammonium oxidation:
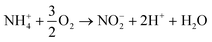 | (10) |
Aerobic nitrite oxidation:
 | (11) |
Anaerobic ammonium oxidation:
| NH+4 + NO−2 → N2 + 2H2O | (12) |
Nine compounds are produced or consumed in these six reactions, but two of the compounds, H2O and N2, are not considered in the mass balances, because the produced amounts are too low compared to the background concentration in water and air.
An overview of the equation system is given in Table 1, and the complete equation system is given in the ESI,† S1. The unknowns to be calculated are the bacterial reaction rates rRj (per day), which could be later used to calculate bacterial activities by multiplying the bacterial reaction rates with the respective stoichiometric coefficients for the substrates.
| System number | System description | Number of mass balances | Number of unknowns | Rank | Rel. std. dev. of AMX conc. |
|---|---|---|---|---|---|
| 1 | Catabolic reactions | 7 (NH4, NO2, NO3, Ac, H, O2, TIC) | 6 (rHET,O2, rHET,NO2, rHET,NO3, rAOB, rNOB, rAMX) | 4 | — |
| 2 | Catabolic and anabolic reactions, no kinetics, no bacterial conc. | 7 (NH4, NO2, NO3, Ac, H, O2, TIC) | 12 (αHET,O2,growth, αHET,O2,end.resp, αHET,NO2,growth, αHET,NO2,end.resp, αHET,NO3,growth, αHET,NO3,end.resp, αAOB,growth, αAOB,end.resp, αNOB,growth, αNOB,end.resp, αAMX,growth, αAMX,end.resp) | 6 | — |
| 3 | Catabolic and anabolic reactions, no kinetics, 1 type of HET | 12 (NH4, NO2, NO3, Ac, H, O2, TIC, XI, XHET, XAOB, XNOB, XAMX) | 12 (αHET,O2,growth, αHET,O2,end.resp, αHET,NO2,growth, αHET,NO2,end.resp, αHET,NO3,growth, αHET,NO3,end.resp, αAOB,growth, αAOB,end.resp, αNOB,growth, αNOB,end.resp, αAMX,growth, αAMX,end.resp) | 9 | — |
| 4 | Catabolic and anabolic reactions, no kinetics, 3 types of HET | 14 (NH4, NO2, NO3, Ac, H, O2, TIC, XI, XHET,O2, XHET,NO2, XHET,NO3, XAOB, XNOB, XAMX) | 12 (αHET,O2,growth, αHET,O2,end.resp, αHET,NO2,growth, αHET,NO2,end.resp, αHET,NO3,growth, αHET,NO3,end.resp, αAOB,growth, αAOB,end.resp, αNOB,growth, αNOB,end.resp, αAMX,growth, αAMX,end.resp) | 11 | — |
| 5 | Catabolic and anabolic reactions, with kinetics, 3 types of HET | 7 (NH4, NO2, NO3, Ac, H, O2, TIC) | 6 (XHET,O2, XHET,NO2, XHET,NO3, XAOB, XNOB, XAMX) | 6 | 5280% |
| 6 | Catabolic and anabolic reactions, with kinetics, without heterotrophic activity | 6 (NH4, NO2, NO3, H, O2, TIC) | 3 (XAOB, XNOB, XAMX) | 3 | 5% |
| 7 | Catabolic and anabolic reactions, with kinetics and sludge loss, 3 types of HET | 8 (NH4, NO2, NO3, Ac, H, O2, TIC, Xtot) | 6 (XHET,O2, XHET,NO2, XHET,NO3, XAOB, XNOB, XAMX) | 6 | 1210% |
2.6 Mass balances based on the activated sludge models (equation systems 2 to 4)
According to ASMs, biological metabolism can be represented by growth and decay of biomass. Both processes are modelled with empirical stoichiometric coefficients. In ASMs, growth inherently includes catabolic and anabolic reactions, whereas decay can be due to anabolic reactions, predation and chemical decomposition (e.g. hydrolysis). In this study, biomass decay was simulated as endogenous respiration. Median values of a literature review were used for the stoichiometric coefficients for growth and decay (Table 2). The biomass composition was assumed to be C5H7O2N for HET, AOB and NOB, while for AMX, the biomass composition given by Strous et al.20 was used (CH2O0.5N0.15).| Symbol | Parameter | Median | Min | Max | Unit |
|---|---|---|---|---|---|
| Y HET,O2 | Yield for growth of XHET with oxygen | 0.630 (ref. 19 and 23) | 0.609 (ref. 29) | 0.800 (ref. 26) | g COD g COD−1 |
| Y HET,NO2 | Yield for growth of XHET with nitrite | 0.540 (ref. 19 and 23) | 0.540 (ref. 19 and 23) | 0.650 (ref. 26) | g COD g COD−1 |
| Y HET,NO3 | Yield for growth of XHET with nitrate | 0.540 (ref. 19 and 23) | 0.540 (ref. 19 and 23) | 0.650 (ref. 26) | g COD g COD−1 |
| Y AOB | Yield for growth of XAOB | 0.210 (ref. 22 and 25) | 0.150 (ref. 21) | 0.292 (ref. 28) | g COD g N−1 |
| Y NOB | Yield for growth of XNOB | 0.046 (ref. 21 and 22) | 0.030 (ref. 25) | 0.059 (ref. 29) | g COD g N−1 |
| Y AMX | Yield for growth of XAMX | 0.150 (ref. 25) | 0.124 (ref. 28) | 0.159 (ref. 20) | g COD g N−1 |
| i N,XI | Nitrogen content of inorganic biomass XI | 0.04 (ref. 26) | 0.02 (ref. 19) | 0.06 (ref. 19) | g N g COD−1 |
| f X I | Fraction of biomass converted into XI during endogenous respiration | 0.18 (ref. 24–27) | 0.08 (ref. 19) | 0.20 (ref. 25 and 26) | — |
Three different equation systems were tested. In equation system 2 (Table 1), only mass balances for dissolved compounds were considered and the mass balances were set up according to eqn (6): instead of the bacterial reaction rates rRj, bacterial activities (αRj) were used as unknowns:
| A·αR = rC | (13) |
| αR,j = rR,j·Xj | (14) |
This approach was used because the stoichiometry of ASMs is given per biomass unit. It should be noted that this approach does not require that Xj values are calculated.
In equation systems 3 and 4 (Table 1), balances for the bacterial groups and inert biomass were also included (see eqn (4)). Most of the previously published models (for example, Kaelin et al.31) assumed that one type of HET can use all three electron acceptors (O2, NO2−, NO3−). In reality, HET biomass will consist of a mixture of heterotrophic bacteria that can use one, two or all three electron acceptors.32 In our study, we compared mass balances with one type of HET that can use all three electron acceptors (equation system 3) and three types of HET which specifically use only one of them (equation system 4).
An overview of the equations systems is given in Table 1. The complete equation systems are given in the ESI,† S2.
2.7 Mass balances based on the activated sludge model including kinetics (equation systems 5 and 6)
In equation systems 5 and 6 (Table 1), the bacterial reaction rates are described with more detailed kinetic expressions:| rRj = ρj·Xj | (15) |
| A·X = rC | (16) |
 | (17) |
 | (18) |
The bacterial reaction rates can subsequently be calculated according to eqn (15). The relevant process rates for a nitritation/anammox reactor with heterotrophic activity are listed in Table 3. Whenever possible, we used median values based on a literature review (Table 4). While the affinity and inhibition constants of AOB, NOB and HET have been documented in several studies, the number of values is sparse for the saturation coefficient of AMX for ammonium (KNH4,AMX) and nitrite (KNO2,AMX) and the inhibition coefficient of AMX for oxygen (KI,O2,AMX). Strous et al.42 reported that both the affinity constants for the substrates ammonium and nitrite are lower than 0.1 mg N L−1. We assumed that KNH4,AMX and KNO2,AMX were 0.1 mg N L−1 each. Strous et al.43 reported that AMX were completely inhibited at 0.5% air saturation, which equals 0.036 mg O2 L−1 at 30 °C. In this study, we assumed that KI,O2,AMX, which corresponds to the oxygen concentration at a 50% inhibition of AMX, was 0.1 mg O2 L−1. For the concentrations of O2, NO2−, NO3−, NH4+ and Ac, we used simulated reference values (section 2.5, Table 5). The complete equation systems are given in the ESI,† S3.
| Symbol | Parameter | Median | Min | Max | Unit |
|---|---|---|---|---|---|
| μ max,HET | Maximum growth rate of XHET | 3.0 (ref. 26) | 2.0 (ref. 19 and 23) | 7.2 (ref. 29) | per day |
| b max,HET | Max. endogenous respiration rate of XHET | −0.3 | per day | ||
| θ T,HET | Temperature dependency of XHET rates | 0.07 (ref. 19 and 26) | °C−1 | ||
| η NOX | Anoxic reduction factor for nitrite and nitrate | 0.7 (ref. 25) | 0.6 (ref. 23) | 0.8 (ref. 19) | — |
| K Ac,HET | Saturation coefficient of XHET for SAc | 4.0 (ref. 19) | 2.0 (ref. 19 and 23) | 20 (ref. 19) | g COD m−3 |
| K O2,HET | Saturation coefficient of XHET for O2 | 0.20 (ref. 19, 23, 26 and 41) | 0.08 (ref. 29) | g O2 m−3 | |
| K NO2,HET | Saturation coefficient of XHET for nitrite | 0.50 (ref. 23, 26 and 41) | 0.14 (ref. 29) | 8.0 (ref. 24) | g N m−3 |
| K NO3,HET | Saturation coefficient of XHET for nitrate | 0.50 (ref. 19, 23, 24, 26 and 41) | 0.12 (ref. 29) | g N m−3 | |
| K I,O2,HET | Inhibition coefficient of XHET for O2 | 2.0 (ref. 24) | g O2 m−3 | ||
| μ max,AOB | Maximum growth rate of XAOB | 0.770 (ref. 29) | 0.481 (ref. 37) | 1.0 (ref. 25) | per day |
| b max,AOB | Max. endogenous respiration rate of XAOB | −0.077 | per day | ||
| θ T,AOB | Temperature dependency of XAOB rates | 0.105 (ref. 25) | 0.094 (ref. 36) | 0.120 (ref. 31) | °C−1 |
| K NH4,AOB | Saturation coefficient of XAOB for ammonium | 1.00 (ref. 24) | 0.14 (ref. 39) | 5.00 (ref. 27) | g N m−3 |
| K O2,AOB | Saturation coefficient of XAOB for O2 | 0.685 (ref. 35, 38) | 0.300 (ref. 29) | 1.66 (ref. 40) | g O2 m−3 |
| μ max,NOB | Maximum growth rate of XNOB | 0.720 (ref. 31 and 36) | 0.341 (ref. 28) | 1.338 (ref. 41) | per day |
| b max,NOB | Max. endogenous respiration rate of XNOB | −0.072 | per day | ||
| θ T,NOB | Temperature dependency of XNOB rates | 0.070 (ref. 25) | 0.061 (ref. 36) | 0.078 (ref. 31) | °C−1 |
| K NO2,NOB | Saturation coefficient of XNOB for nitrite | 1.55 (ref. 29 and 38) | 0.280 (ref. 39) | 3.00 (ref. 24) | g N m−3 |
| K O2,NOB | Saturation coefficient of XNOB for O2 | 1.05 (ref. 24) | 0.470 (ref. 39) | 3.00 (ref. 40) | g O2 m−3 |
| μ max,AMX | Maximum growth rate of XAMX | 0.029 (ref. 28 and 36) | 0.020 (ref. 34) | 0.080 (ref. 25) | per day |
| b max,AMX | Max. endogenous respiration rate of XAMX | −0.0029 | per day | ||
| θ T,AMX | Temperature dependency of XAMX rates | 0.093 (ref. 36) | 0.090 (ref. 36) | 0.096 (ref. 25) | °C−1 |
| Net conversion rates | With HET | Without HET | Biomass conc. [g COD m−3] | With HET | Without HET | Comp. conc. in reactor | With HET | Without HET | ||
|---|---|---|---|---|---|---|---|---|---|---|
| r S O2 | [g O2 m−3 per day] | −507 | −500 | X HET,O2 | 3550 | 0 | S NH4 | [g N m−3] | 1.18 | 1.15 × 10−1 |
| r S Ac | [g COD m−3 per day] | −266 | 0 | X HET,NO3 | 1340 | 0 | S NO2 | [g N m−3] | 2.19 × 10−2 | 3.16 × 10−1 |
| r S NH4 | [g N m−3 per day] | −209 | −209 | X HET,NO2 | 334 | 0 | S NO3 | [g N m−3] | 2.59 × 10−2 | 190 |
| r S NO3 | [g N m−3 per day] | 7.76 × 10−3 | 56.9 | X AOB | 2030 | 684 | S O2 | [g O2 m−3] | 7.11 × 10−3 | 1.16 × 10−1 |
| r S NO2 | [g N m−3 per day] | 6.58 × 10−3 | 9.49 × 10−2 | X NOB | 0 | 74.2 | S Ac | [g COD m−3] | 6.99 × 10−1 | 890 |
| r S H | [g H m−3 per day] | 10.8 | 19.0 | X AMX | 1100 | 691 | ||||
| r S TIC | [g C m−3 per day] | 61.6 | −6.93 | |||||||
| r X tot | [g COD m−3 per day] | 104 | 19.3 | |||||||
2.8 Mass balances based on the activated sludge model including kinetics and a biomass balance (equation system 7)
Equation system 5 can be extended with a biomass balance according to | (19) |
2.9 Reference data for conversion rates
Computer simulations with the software Aquasim44 were used to obtain reference data for solving the mass balances (equation systems 5 to 7). Measurements from a single-stage sequencing batch reactor with five times diluted urine (influent COD/N ratio 1.27 g COD g N−1)45 were used as influent concentrations and as initial conditions (ESI,† S5). All compounds included in the model are listed in the ESI,† S6. The stoichiometric constants and the kinetic constants were the same as given in Tables 2 and 4. Three groups of HET were introduced to represent the heterotrophic activity with oxygen, nitrite and nitrate as electron acceptors. In the case of equation system 6, the initial biomass concentrations of the three groups of HET were set to zero and all heterotrophic processes were inactivated. The simulation of pH equilibria and aeration effects is described in the ESI,† S7. Long-term simulations with constant influent rates were used to approximate concentrations at steady state. The simulated net conversion rates and the biomass concentrations at steady state are listed in Table 5.2.10 Evaluating structural observability
To solve a linear equation system, we need at least as many independent equations (mass balances) as unknown variables (bacterial reaction rates, bacterial activities or biomass concentrations). Independent means that none of the equations can be linearly combined and transformed to another of the available equations. Practically, the classification of the considered equation systems and observability of the unknowns is based on the evaluation of the rank of the linear equation system: the rank must be equal to the number of unknowns; otherwise, the linear equation system is under-determined.When empirically determined stoichiometric parameters are used, the equation system might be underdetermined due to a particular choice of parameter values and not due to an under-determination of the equation system for all feasible parameter values. In this case, the lack of observability would not be structural but only practical. To test whether the lack of observability is not only practical but also structural, we performed Monte Carlo simulations: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations were done with uniformly and randomly distributed parameter values in a range of ±50% of the default values (median values from the literature according to Tables 2 and 4). If this test does not provide any parameter sets, which make the equation system observable, it is very likely that the lack of observability is structural. A stringent test of the structural observability would be considerably more complex46 and was considered to be unnecessary to obtain conclusive results. All computations were executed by means of MATLAB (R2013b, The MathWorks Inc., Natick, MA, USA). The Matlab codes are given in the ESI,† S8 and S9.
000 simulations were done with uniformly and randomly distributed parameter values in a range of ±50% of the default values (median values from the literature according to Tables 2 and 4). If this test does not provide any parameter sets, which make the equation system observable, it is very likely that the lack of observability is structural. A stringent test of the structural observability would be considerably more complex46 and was considered to be unnecessary to obtain conclusive results. All computations were executed by means of MATLAB (R2013b, The MathWorks Inc., Natick, MA, USA). The Matlab codes are given in the ESI,† S8 and S9.
2.11 Evaluating practical observability
If the test for structural observability was successful, we tested the practical observability by estimating the theoretical standard deviations of the estimates. To this end, we assumed that the net conversion rates rCi have a standard deviation of 5% of their steady-state value. In practise, these standard deviations are due to measurement errors and can be higher than 5% so that the computed standard deviations are rather optimistic (i.e., low). In real systems, the variation is probably even larger due to imprecise parameter values. Furthermore, parameter values and analytical measurements of variables can be systematically wrong, leading to systematic estimation errors (bias). Assuming that measurement errors for the rate measurements, rCi, are drawn independently from a normal distribution with zero mean and a given standard deviation (σrCi), one can compute the expected value for the bacterial concentrations Xj in equation systems 5 to 7 (Table 1) as follows:47| A·X = rC | (20) |
X = (AT·∑rC−1·A)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) · ·![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AT·∑rC−1·rC = P·rC AT·∑rC−1·rC = P·rC | (21) |
 | (22) |
∀k,l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k ≠ l ⇒ ∑rS(k,l) = 0 k ≠ l ⇒ ∑rS(k,l) = 0 | (23) |
The variance–covariance matrix for the rate estimates is then given as follows:
| ∑Xj = P·∑rC·PT | (24) |
With the individual standard deviations for the rate estimates computed from the variances on its diagonal, the standard deviation of the biomass estimate becomes
| σXj = (∑Xj(j,j))1/2 | (25) |
In practise, the standard deviation of the net conversion rates can be reduced by means of independent repetitions of the measurements under the same experimental conditions. The standard deviation of the average of r independent measurements can be estimated by dividing the standard deviation of a single measurement by the square root of the total number of measurements r:
| σXj,r = σXj,r/r1/2 | (26) |
3 Results
The setup of the mass balances and the main results are summarised in Table 1. The results will be explained in more detail in the following paragraphs.3.1 Mass balances based on catabolic reactions only
Catabolic reactions alone do not allow the determination of the activities of the different bacterial groups. The linear system consists of seven equations, but the rank of the matrix is only four (Table 1, system 1), which means that three out of the seven equations can be expressed as linear combinations of four independent equations. The lack of observability is thus structural in the sense that it is impossible to conceive any experiment, even idealised, that permits simultaneous estimation of all reaction rates. In contrast to ASM reactions (see section 3.2), the stoichiometric coefficients are known constants that follow directly from the definition of the considered chemical reactions. As such, this result is universal in the sense that it does not depend on any adjustable model parameter.Even if the linear equation system for the catabolic reactions were solvable, the resulting bacterial reaction rates would most probably not be accurate due to some coarse simplifications. The basic assumption that biomass growth and decay are in equilibrium is practically never the case in a wastewater treatment plant. Biomass losses via the effluent or biomass withdrawal cannot be avoided. Furthermore, the catabolic reaction for AMX does not consider an important contribution of AMX to nitrate production: in order to generate the required energy for carbon fixation, AMX oxidise nitrite to nitrate, accounting for 11% of the total N conversion by AMX.20
3.2 Mass balances based on the activated sludge model
When considering microbial metabolism according to ASMs, the number of unknowns increases to twelve: for each of the six bacterial groups, two bacterial rates – growth and endogenous respiration – are included. In the equation system, there are now more unknowns (twelve) than mass balances (seven) which means no unique solution exists under any scenario (Table 1, system 2). Concentrations for NOB, AOB, AMX, HET and for inert biomass can be included to provide additional measurements and associated balancing equations. Despite the inclusion of such measurements which are hard to obtain in practise, it remains impossible to determine the microbial activities (Table 1, system 3). This is also the case when the HET are divided in three subgroups, which use oxygen, nitrite or nitrate as electron acceptors (Table 1, system 4). The same classification was obtained for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random sets for the parameter values. This suggests that the lack of observability is most probably structural and not due to a particular combination of estimated parameters.
000 random sets for the parameter values. This suggests that the lack of observability is most probably structural and not due to a particular combination of estimated parameters.
Even if it were possible to compute values for the considered respiration rates, it is worth considering that empirical stoichiometric coefficients have to be included in the mass balances (Table 2). These are considered to be known exactly, although such parameters are estimated in practise. This means that the balancing equations as described here are subject to additional unaccounted uncertainty in practise.
3.3 Mass balances based on the activated sludge model including kinetics
When the kinetics are known, one can combine the growth and endogenous respiration for each type of bacteria into a single net growth rate. This reduces the number of unknowns from twelve to six and allows the determination of the biomass concentrations and thereby the bacterial activities (Table 1, system 5). In this case, and for the first time in this study, the balancing matrix A is full rank. This means that the concentrations of AOB, NOB, and AMX and the hypothetical concentrations of the three groups of HET can be estimated (structural observability). The activities for growth and endogenous respiration can later be calculated with the assumed kinetic expressions.Although the biomass concentrations can be determined, the uncertainty of the resulting values is immense when using a single set of rate measurements (Table 6). Assuming that all necessary stoichiometric and kinetic parameters (Tables 2 and 4) are known exactly, the relative standard deviations of the bacterial activities equal the relative standard deviations of the calculated biomass concentrations and only depend on the measurement accuracy of the net conversion rates. Even if a low standard deviation of 5% is assumed for the conversion rate measurements, the resulting standard deviations for the biomass concentrations are extremely high: the relative standard deviation for AMX is 5280% (Table 6).
| With HET | Without HET | |||||
|---|---|---|---|---|---|---|
| Including kinetics | Including kinetics and biomass balance | Including kinetics | ||||
| Concentration (mg COD L−1) | % St. dev. (%) | Concentration (mg COD L−1) | % St. dev. (%) | Concentration (mg COD L−1) | % St. dev. (%) | |
| X HET,O2 | 3470 | 9420 | 3510 | 2120 | ||
| X HET,NO3 | 1290 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
1310 | 3590 | ||
| X HET,NO2 | 483 | 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
413 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
||
| X AOB | 2040 | 3620 | 2030 | 846 | 684 | 2.4 |
| X NOB | −181 | 345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
−103 | 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
74.0 | 8.4 |
| X AMX | 1080 | 5280 | 1090 | 1210 | 694 | 4.9 |
The most likely explanation for the high uncertainties of the calculated biomass concentrations is that the mass balances are close to linearly dependent. Removing the heterotrophic activities from the equation system in particular is expected to improve the estimation precision. Nitrogen can then only be removed via nitritation/anammox and not by a second parallel metabolic pathway (nitrification/denitrification), which strongly reduces the number of estimated unknowns. We demonstrate that this is indeed the case by applying the same mass balances for a completely autotrophic system (Table 1, system 6). With a relative standard deviation of 5% for the net conversion rates, the resulting relative standard deviations for the calculated concentrations of AOB, NOB and AMX are now below 10% (Table 6).
The high relative standard deviations of the calculated biomass concentrations can also be reduced by including a mass balance for the biomass (Table 1, equation system 7) to the original equation system (including HET activity). In our example, the relative standard deviation for AMX becomes 1210%. However, this standard deviation is still unrealistically high for practical purposes. The standard deviations of the net conversion rates can be reduced although with multiple measurements. As an example, the required number of measurements and the corresponding standard deviation of the net conversion rates to reach a certain standard deviation for the calculated biomass concentration of AMX are listed in Table 7. To achieve a relative standard deviation of 50% for the AMX concentration, about 600 measurements of the net conversion rates would be necessary under the same experimental conditions. This number is however still too high for measurements based on conventional grab sampling. Therefore, we conclude that neither AMX activity nor any other of the considered bacterial activities is practically observable with mass balances and conventional grab sampling.
| Desired % st. dev. of XAMX | Required % st. dev. of the net conversion rates | Required number of measurements if % st. dev. of one measurement is 5% |
|---|---|---|
| 50 | 0.205 | 595 |
| 40 | 0.164 | 929 |
| 30 | 0.123 | 1651 |
| 20 | 0.082 | 3713 |
| 10 | 0.041 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
4 Discussion
4.1 Constraints are necessary for the structural observability of the linear equation system
By including constraints, i.e., kinetic expressions, we achieved complete structural observability of all unknown parameters (Table 1, systems 5 and 6). This approach is similar to the flux balance analysis, which is a common method to analyse the metabolic networks of single microorganisms.48 To overcome the lack of detailed information about the metabolism of a bacterial cell, the metabolic network is represented by a stoichiometric matrix describing the relation of conversion rates and metabolic reactions at steady state. The resulting equation system49 has essentially the same form as our equation systems, and it is usually not observable because the number of unknown reactions is larger than the number of compounds.50 Constraints are introduced, e.g., measured fluxes or boundaries for certain rates, to allow quantitative predictions. Concentrations, e.g., of metabolites, cannot be predicted, because accurate kinetic parameters are usually not available.50 Here is the difference to our approach: our systems do not consist of single cells but of bacterial populations, for which macroscopic kinetic data are available. By including the kinetic data (systems 5 and 6 in Table 1), all unknown variables, i.e. bacterial concentrations, are observable.Including kinetics makes the linear equation system structurally observable but also affects the accuracy of the final result. Systematic errors can be included in the mass balance. As the data compilation in Table 4 shows, literature values for kinetic parameters vary widely and the chosen kinetic expressions might not include critical influences such as inhibition of AMX or AOB. However, unexpected inhibition effects by unknown compounds are a frequent problem in wastewater treatment plants.51
It would be desirable to achieve observability of all reaction rates by increasing the number of independent mass balance equations and not using kinetics. In theory, at least two additional mass balances could be included in our systems: one for H2O and one for N2. Unfortunately, no conversion rates for the two compounds can be measured, because their background concentrations are far too high. Furthermore, the two additional equations are not independent from the others (data not shown), so that the rank of the previous mass balances does not increase. Another option would be to include side products such as nitrous oxide (N2O) or nitric oxide (NO). Both compounds can be measured in the off-gas52 or with sensors directly in the water.53 The isotopic signatures of N2O even allow the differentiation of the production pathway.54 However, both compounds are side products, which only occur under certain circumstances. Additional reaction rates would have to be included to balance those compounds, so that structural observability of the bacterial activities would still not be achieved without introducing kinetics. Based on these considerations, including constraints (e.g. as kinetic expressions) seems to be the only way to achieve structural observability of the bacterial activities with the linear equation systems in our study.
4.2 Additional mass balances could be used to achieve practical observability
Our study shows that not only increasing the number of measurements but also increasing the number of equations can improve the precision of the biomass concentration estimates. Adding one more equation (biomass balance) to equation system 5 led to a substantial reduction of the variability of the estimated biomass concentrations in equation system 7. This is due to the fact that some conversion rates are redundant and could also be calculated by combining other mass balances. In other words, some conversion rates can be balanced.55 In practical systems, such redundancy can be used to detect and remove systematic balancing errors (gross error detection) and to reduce random measurement errors in measured data. The latter is also known as data reconciliation.56Data reconciliation is a common procedure for industrial processes. It has been proposed for wastewater treatment as well57 but is not commonly applied. This is partly due the fact that municipal wastewater treatment plants usually do not comply with certain requirements of the most basic data reconciliation methods: most of the processes are not at steady state, the variances of process variables are not known and some measurements often have gross errors.58 Recently, methods have been adapted for wastewater treatment and now allow the identification of periods with gross measurement errors, e.g. based on the CUSUM statistic for linear mass balancing errors59 or based on bilinear mass balancing equations.60 Furthermore, the ability to detect measurement errors via mass balancing can be ensured by optimising the location of sampling.61 Long periods under quasi-steady-state conditions and without gross errors can provide a sufficiently high number of measurements to allow the calculation of precise biomass concentrations (Table 7). The result would be an average biomass concentration during an extended period of time.
Our study showed that not only increasing the number of measurements but also increasing the number of equations while retaining the same number of unknowns can improve the precision of the biomass concentrations. Adding one more equation (biomass balance) led to a substantial reduction of the variability of the final result.
4.3 Observing dynamics and separating bacterial processes can provide additional information
The approach used in this study is based on two basic requirements for reactor operation: first, the soluble and particulate compounds are in steady state, and second, all processes occur concomitantly in one single reactor. However, reactors with higher dynamics, such as sequencing batch reactors, and separating the aerobic and the anoxic process steps in two different reactors, are likely better suited to determine the bacterial activities on a regular basis. Short-term changes from single-stage operation to a cyclic multi-stage operation could also be used as an online experimental design method to obtain observability at regular time intervals.Dynamic measurements allow for more information about the processes, but a prerequisite for practical applications is the use of sensors. If online measurements are available, not only the actual concentrations but also mathematical derivatives such as the oxygen consumption or the change in the oxygen consumption can be used to determine unknown activities.62 Oxygen and ammonia sensors have been applied successfully for online observation of AMX activity in large-scale wastewater treatment plants.9 Nitrite sensors would further simplify the observation of AMX activity, but reliable nitrite sensors, especially for high nitrite concentrations, still have to be developed.1,63
By operating the nitritation/anammox process in two reactors64 or during two phases in the same reactor,1 aerobic processes such as the activities of AOB, NOB and aerobic HET could be separated from anoxic activities such as AMX and heterotrophic denitrification. While such an approach would greatly simplify the quantification of AMX activity, operational problems such as N2O production,65 high NOB activity66 or inhibition of AMX can occur due to nitrite overloading.9 For such reasons, most full scale nitritation/anammox reactors are operated as single-stage systems,51 although two-stage systems would easily render the AMX activity observable. However, in single-stage systems, short phases with alternating aeration could be introduced to determine the AMX activity.
5 Conclusions
• In theory, mass balances can be used to determine the AMX activity in a nitritation/anammox reactor with heterotrophic activity, but the requirements are challenging. Based on our study, there are three necessary conditions:– Accurate values for the stoichiometric and the kinetic parameters are available for all considered reactions.
– The process can be assumed to operate in steady state.
– A large number of reliable measurements are available for flow rates, COD, nitrite, nitrate, ammonium, alkalinity, TIC, pH and oxygen.
• To achieve a satisfying precision for the estimated AMX activity, an immense number of independent measurements are required. In our example, the conversion rates would need to have standard deviations as low as 0.2% to achieve a precision of 50% for the AMX concentration. This high precision for the conversion rates is practically unachievable with grab samples and laboratory measurements. In the future, high-frequency measurements with sensors and data reconciliation methods could allow for such a high precision of conversion rates.
Acknowledgements
This work was financed by the Swiss National Science Foundation under grant 200020_144498 (Decentralised urine treatment with the nitritation/anammox process, DUNOX, Part 2).References
- A. Joss, N. Derlon, C. Cyprien, S. Burger, I. Szivak, J. Traber, H. Siegrist and E. Morgenroth, Environ. Sci. Technol., 2011, 45, 9735–9742 CrossRef CAS PubMed.
- S. Jenni, S. E. Vlaeminck, E. Morgenroth and K. M. Udert, Water Res., 2014, 49, 316–326 CrossRef CAS PubMed.
- S. M. Podmirseg, T. Pümpel, R. Markt, S. Murthy, C. Bott and B. Wett, Water Res., 2015, 68, 194–205 CrossRef PubMed.
- A. Daverey, S.-H. Su, Y.-T. Huang and J.-G. Lin, Bioresour. Technol., 2012, 113, 225–231 CrossRef CAS PubMed.
- C. Pellicer-Nàcher, S. Sun, S. Lackner, A. Terada, F. Schreiber, Q. Zhou and B. F. Smets, Environ. Sci. Technol., 2010, 44, 7628–7634 CrossRef PubMed.
- A. G. Mutlu, A. K. Vangsgaard, G. Sin and B. F. Smets, Water Sci. Technol., 2013, 68, 514–521 CrossRef CAS PubMed.
- T. Kindaichi, T. Ito and S. Okabe, Appl. Environ. Microbiol., 2004, 70, 1641–1650 CrossRef CAS.
- S. Okabe, T. Kindaichi and T. Ito, Appl. Environ. Microbiol., 2005, 71, 3987–3994 CrossRef CAS PubMed.
- A. Joss, D. Salzgeber, J. Eugster, R. König, K. Rottermann, S. Burger, P. Fabijan, S. Leumann, J. Mohn and H. Siegrist, Environ. Sci. Technol., 2009, 43, 5301–5306 CrossRef CAS.
- W. R. L. van der Star, W. R. Abma, D. Blommers, J.-W. Mulder, T. Tokutomi, M. Strous, C. Picioreanu and M. C. M. van Loosdrecht, Water Res., 2007, 41, 4149–4163 CrossRef CAS PubMed.
- B. Wett, Water Sci. Technol., 2007, 56, 81–88 CrossRef CAS PubMed.
- K. M. Udert, T. A. Larsen and W. Gujer, Water Sci. Technol., 2006, 54, 413–420 CAS.
- K. M. Udert, E. Kind, M. Teunissen, S. Jenni and T. A. Larsen, Water Sci. Technol., 2008, 58, 277–284 CrossRef CAS PubMed.
- H. De Clippeleir, S. E. Vlaeminck, F. Wilde, K. Daeninck, M. Mosquera, P. Boeckx, W. Verstraete and N. Boon, Appl. Microbiol. Biotechnol., 2013, 97, 10199–10210 CrossRef CAS PubMed.
- M. K. H. Winkler, R. Kleerebezem and M. C. M. van Loosdrecht, Water Res., 2012, 46, 136–144 CrossRef CAS PubMed.
- L. Jia, J.-S. Guo, F. Fang, Y.-P. Chen and Q. Zhang, Environ. Technol., 2012, 33, 1141–1149 CrossRef CAS PubMed.
- C.-J. Lan, M. Kumar, C.-C. Wang and J.-G. Lin, Bioresour. Technol., 2011, 102, 5514–5519 CrossRef CAS PubMed.
- C.-C. Wang, P.-H. Lee, M. Kumar, Y.-T. Huang, S. Sung and J.-G. Lin, J. Hazard. Mater., 2010, 175, 622–628 CrossRef CAS PubMed.
- M. Henze, W. Gujer, T. Mino and M. van Loosdrecht, Scientific and Technical Reports No. 9, IWA Publishing, London, 2000 Search PubMed.
- M. Strous, J. J. Heijnen, J. G. Kuenen and M. S. M. Jetten, Appl. Microbiol. Biotechnol., 1998, 50, 589–596 CrossRef CAS.
- E. Alpkvist, C. Picioreanu, M. C. M. van Loosdrecht and A. Heyden, Biotechnol. Bioeng., 2006, 94, 961–979 CrossRef CAS PubMed.
- F. Fang, B.-J. Ni, X.-Y. Li, G.-P. Sheng and H.-Q. Yu, Appl. Microbiol. Biotechnol., 2009, 83, 1159–1169 CrossRef CAS PubMed.
- W. Gujer, M. Henze, T. Mino and M. van Loosdrecht, Water Sci. Technol., 1999, 39, 183–193 CrossRef CAS.
- M. J. Kampschreur, C. Picioreanu, N. Tan, R. Kleerebezem, M. S. M. Jetten and M. C. M. van Loosdrecht, Water Environ. Res., 2007, 79, 2499–2509 CrossRef CAS.
- G. Koch, K. Egli, J. R. Van Der Meer and H. Siegrist, Water Sci. Technol., 2000, 41, 191–198 CAS.
- G. Koch, M. Kühni, W. Gujer and H. Siegrist, Water Res., 2000, 34, 3580–3590 CrossRef CAS.
- M. S. Moussa, C. M. Hooijmans, H. J. Lubberding, H. J. Gijzen and M. C. M. van Loosdrecht, Water Res., 2005, 39, 5080–5098 CrossRef CAS PubMed.
- A. K. Vangsgaard, A. G. Mutlu, K. V. Gernaey, B. F. Smets and G. Sin, J. Chem. Technol. Biotechnol., 2013, 88, 2007–2015 CAS.
- U. Wiesmann, Adv. Biochem. Eng./Biotechnol., 1994, 51, 113–154 CrossRef CAS.
- S. Wyffels, S. W. H. Van Hulle, P. Boeckx, E. I. P. Volcke, O. V. Cleemput, P. A. Vanrolleghem and W. Verstraete, Biotechnol. Bioeng., 2004, 86, 531–542 CrossRef CAS PubMed.
- D. Kaelin, R. Manser, L. Rieger, J. Eugster, K. Rottermann and H. Siegrist, Water Res., 2009, 43, 1680–1692 CrossRef CAS PubMed.
- K. T. van De Pas-Schoonen, S. Schalk-Otte, S. Haaijer, M. Schmid, H. Op Den Camp, M. Strous, J. G. Kuenen and M. S. M. Jetten, Biochem. Soc. Trans., 2005, 33, 205–209 CrossRef CAS PubMed.
- S. Lackner, A. Terada and B. F. Smets, Water Res., 2008, 42, 1102–1112 CrossRef CAS PubMed.
- A. Dapena-Mora, S. W. H. Van Hulle, J. L. Campos, R. Mendez, P. A. Vanrolleghem and M. S. M. Jetten, J. Chem. Technol. Biotechnol., 2004, 79, 1421–1428 CrossRef CAS PubMed.
- A. Guisasola, I. Jubany, J. A. Baeza, J. Carrera and J. Lafuente, J. Chem. Technol. Biotechnol., 2005, 80, 388–396 CrossRef CAS PubMed.
- X. Hao, J. J. Heijnen and M. C. M. van Loosdrecht, Water Res., 2002, 36, 4839–4849 CrossRef CAS.
- J. H. Hunik, C. G. Bos, M. P. van den Hoogen, C. D. De Gooijer and J. Tramper, Biotechnol. Bioeng., 1994, 43, 1153–1163 CrossRef CAS PubMed.
- S. Jayamohan, S. Ohgaki and K. Hanaki, Water Supply, 1988, 6, 141–150 CAS.
- R. Manser, W. Gujer and H. Siegrist, Water Res., 2005, 39, 4633–4642 CrossRef CAS PubMed.
- O. Sánchez, M. C. Martí, E. Aspé and M. Roeckel, Biotechnol. Lett., 2001, 23, 1597–1602 CrossRef.
- B. Wett and W. Rauch, Water Res., 2003, 37, 1100–1110 CrossRef CAS.
- M. Strous, J. G. Kuenen and M. S. M. Jetten, Appl. Environ. Microbiol., 1999, 65, 3248–3250 CAS.
- M. Strous, E. Van Gerven, J. G. Kuenen and M. Jetten, Appl. Environ. Microbiol., 1997, 63, 2446–2448 CAS.
- P. Reichert, AQUASIM 2.1e – Computer program for the identification and simulation of aquatic systems, Eawag, Dübendorf, 1998 Search PubMed.
- H. Bürgmann, S. Jenni, F. Vazquez and K. M. Udert, Appl. Environ. Microbiol., 2011, 77, 5897–5907 CrossRef PubMed.
- I. Ponzoni, M. C. Sánchez and N. B. Brignole, Ind. Eng. Chem. Res., 1999, 38, 3027–3035 CrossRef CAS.
- S. Narasimhan and C. Jordache, Data reconciliation and gross error detection: An intelligent use of process data, Gulf Professional Publishing, 1999 Search PubMed.
- J. S. Edwards, M. Covert and B. Palsson, Environ. Microbiol., 2002, 4, 133–140 CrossRef.
- H. J. Noorman, J. J. Heijnen and K. C. A. M. Luyben, Biotechnol. Bioeng., 1991, 38, 603–618 CrossRef CAS PubMed.
- J. D. Orth, I. Thiele and B. O. Palsson, Nat. Biotechnol., 2010, 28, 245–248 CrossRef CAS PubMed.
- S. Lackner, E. M. Gilbert, S. E. Vlaeminck, A. Joss, H. Horn and M. C. M. van Loosdrecht, Water Res., 2014, 55, 292–303 CrossRef CAS PubMed.
- F. Schreiber, P. Wunderlin, K. M. Udert and G. F. Wells, Front. Microbiol., 2012, 3, 372–372 Search PubMed.
- S. Jenni, J. Mohn, L. Emmenegger and K. M. Udert, Environ. Sci. Technol., 2012, 46, 2257–2266 CrossRef CAS PubMed.
- P. Wunderlin, M. F. Lehmann, H. Siegrist, B. Tuzson, A. Joss, L. Emmenegger and J. Mohn, Environ. Sci. Technol., 2012, 47, 1339–1348 Search PubMed.
- R. T. J. M. van Der Heijden, J. J. Heijnen, C. Hellinga, B. Romein and K. C. A. M. Luyben, Biotechnol. Bioeng., 1994, 43, 3–10 CrossRef CAS PubMed.
- H. J. Noorman, B. Romein, K. C. A. M. Luyben and J. J. Heijnen, Biotechnol. Bioeng., 1996, 49, 364–376 CrossRef CAS.
- S. C. F. Meijer, H. van der Spoel, S. Susanti, J. J. Heijnen and M. C. M. van Loosdrecht, Water Sci. Technol., 2002, 45, 145–156 CAS.
- A. Spindler, Water Res., 2014, 57, 193–201 CrossRef CAS PubMed.
- A. Spindler and P. A. Vanrolleghem, Water Sci. Technol., 2012, 65, 2148–2153 CrossRef CAS PubMed.
- K. Villez, L. Corominas and P. A. Vanrolleghem, in Proceedings of the 11th IWA conference on instrumentation control and automation, Narbonne, France, 2013 Search PubMed.
- K. Villez, L. Corominas and P. A. Vanrolleghem, in 2nd IWA New Developments in IT & Water conference, Rotterdam, the Netherlands, 2015 Search PubMed.
- D. Dochain, P. A. Vanrolleghem and M. Van Daele, Water Res., 1995, 29, 2571–2578 CrossRef CAS.
- A. Mašić and K. Villez in Conference proceedings of the 2nd IWA Specialized International Conference “Ecotechnologies for Wastewater Treatment”, Verona, Italy, 2014 Search PubMed.
- U. van Dongen, M. S. M. Jetten and M. C. M. van Loosdrecht, Water Sci. Technol., 2001, 44, 153–160 CAS.
- M. J. Kampschreur, W. R. L. van der Star, H. A. Wielders, J. W. Mulder, M. S. M. Jetten and M. C. M. van Loosdrecht, Water Res., 2008, 42, 812–826 CrossRef CAS PubMed.
- C. Fux, D. Huang, A. Monti and H. Siegrist, Water Sci. Technol., 2004, 49, 53–60 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ew00045a |
| This journal is © The Royal Society of Chemistry 2015 |