Geometrically confined favourable ion packing for high gravimetric capacitance in carbon–ionic liquid supercapacitors†
Xuehang
Wang
a,
Haitao
Zhou
a,
Edel
Sheridan
b,
John Charles
Walmsley
b,
Dingding
Ren
c and
De
Chen
*a
aDepartment of Chemical Engineering, Norwegian University of Science and Technology, Sem Sælands vei 4, 7491 Trondheim, Norway. E-mail: de.chen@ntnu.no; Fax: +47 735 95047; Tel: +47 735 93149
bSINTEF Materials and Chemistry, 7491 Trondheim, Norway
cDepartment of Electronics and Telecommunications, Norwegian University of Science and Technology, 7491 Trondheim, Norway
First published on 12th November 2015
Abstract
A supercapacitor, a safe and durable electrical energy storage device with fast charge–discharge capability, will achieve more widespread use if the specific energy can be improved. However, current understanding of pore characteristic effects on gravimetric capacitance has limited the development of electrode materials. We derive a model of ion packing in cylindrical nanopores, and it quantitatively reveals the significant impact of pore geometric characteristics on the gravimetric capacitance in neat ionic liquid, which is confirmed experimentally using a series of sponge-like carbons (carbon nanosponge). With the favourable ion packing proposed by the model, the electrode using the carbon nanosponge as an active material delivered double-layer capacitances of 290 F g−1 (20 °C) and 387 F g−1 (60 °C) with an operating cell voltage of 4 V. This study also provides systematical strategies for rational design of various carbon materials and ionic liquids by optimized ion packing for ultrahigh gravimetric capacitance.
Broader contextSupercapacitor, a safe and durable electrical energy storage device with high power capability, is competitive to meet the increasing need for high power energy storage in renewable energy and electric vehicles. However, the moderate energy densities of the supercapacitors limit their wide-spread use compared to the batteries. The adsorption of ions (cations and anions form ionic liquid electrolytes) in the pores of the carbon materials in a electrode is the crucial factor to determine the specific capacitance of carbon materials. In this work, we developed a model of ion packing, and it reveals the significant impact of geometric factors, mainly three parameters such as pore size distribution, ionic size and pore volume, on the gravimetric capacitance quantitatively. The model predicting ultrahigh capacitance can be achieved by optimizing the three parameters. Due to the geometric-confined favourable ion packing, the mesopore-rich carbon nanosponges synthesized by a facile method in this work delivered high capacitance and high full-packaged specific energy comparable to NiMH batteries. By combining modeling and insights into carbon nanomaterial synthesis and characterization, it has been possible to go beyond our fundamental understanding to the design of carbon–ionic liquid systems for energy storage. |
Introduction
Supercapacitors (SCs, also known as electrochemical capacitors), possessing excellent high output power capability, long cycling life and safety performance, are the competitive energy storage option to meet the increasing power demand in the portable energy storage devices (for example electrical vehicles) and grid energy storage for renewable energy sources.1–5 However, wide-scale applications of commercial carbon-based SCs are hindered by their poor specific energy, of 4–5 Watt hour (W h) kg−1, compared to that of the nickel–metal hydride (NiMH) batteries (60–100 W h kg−1).1 To improve the specific energy of SCs, efforts have been devoted to improving the DL capacitance of the carbon electrode and increasing the operational voltage range by using the ionic liquid (IL) electrolyte.SCs store energy by accumulating charges to form electrical double layers (DLs) at the interface between the electrode surface and the electrolyte. Thus, a high surface area which provides good ion-accessibility should result in high capacitance.4 However it has been shown not necessary to be the case.6 An alternative method to improve the capacitance is to incorporate the pseudo-capacitive material (metal oxides or conductive polymers) with the carbon material.7,8 This can introduce some drawbacks simultaneously, including shorter cycling life, higher cost and smaller voltage window.9
Optimization of the pore size is an important approach to improve the DL capacitance, as both the ion-accessible specific surface area (SSA) and the normalized capacitance (capacitance per surface area) are related to the pore size.9–16 For a given porous carbon, the highest achievable normalized capacitance in ILs was observed when the average pore size matched the ion size of the IL electrolyte.10,11 Meanwhile, a narrow pore size distribution (PSD) has been suggested to be crucial in reaching the maximal normalized capacitance.13 However, for a large variety of carbon materials, such as activated carbon (AC), graphene, activated graphene and even ordered mesoporous carbon, it is difficult to offer a perfect-controlled narrow PSD (width < 1 nm),1,6,17–22 and the micropores are usually not favourable for quick ion transportation. Carbon material design based on current understandings is insufficient to improve the SC specific energy approaching batteries without sacrificing the specific power.
The geometric influence of the pores has been studied intensively to understand its effect on the capacitance.12–15 The elimination of the so-called overscreening effect, caused by the geometric limitation of the pore size,12 which describes well the capacitance enhancement in the microporous region, could not be applied to a larger pore size. A model, assuming ions are lined-up in a cylindrical pore, fits well the capacitances of micropores,14 but the goodness of fitting in the mesoporous region is low, as the average pore size cannot comprehensively represent the PSD with non-ignorable width.13 According to one study by molecular dynamics (MD) simulation, the geometry factor of the cylindrical pore size was found to result in different ion distributions,15 which impact on the number of adsorbed charged ions and hence the capacitance. However, the estimated normalized capacitances of this ion-distribution structure did not agree quantitatively with the experimental ones.
In this study, we synthesized a series of sponge-like porous carbon materials, namely carbon nanosponge (CNS), with Brunauer–Emmett–Teller (BET) SSA values of up to 3464 m2 g−1via a facile and scalable method as shown in Fig. S1a (ESI†). Despite the relative broad PSD (∼7 nm) and mesopore-rich structure, the highest DL capacitances and normalized capacitance (BET) delivered by CNSs in ILs are 290 F g−1 and 15.6 μF cm−2, respectively. The normalized capacitance was even higher than the micropore-only titanium carbide-derived carbon of 13.5 μF cm−2.11 We derived a model of geometrically confined ion packing in cylindrical nanopores, and it well estimates the gravimetric capacitances based on the PSDs of the CNS and other reported carbon materials. Upon favourable ion packing at elevated temperature, the CNS (CNS1, code in Table S1, ESI†) delivered a DL capacitance of 387 F g−1 with a large operating cell voltage of 4 V, corresponding to an unprecedented high specific energy of 204 W h kg−1 for SCs.
Experimental
Synthesis of the CNSs
CNSs were generally prepared by a three-step process (Fig. S1a, ESI†). The polyaniline (PANI) nanofiber was prepared from an aniline monomer by a rapid-mix method developed by Huang et al.23 1 mol L−1 of HCl solution containing 30.0 g L−1 of aniline (Sigma-Aldrich) was mixed quickly with 1 mol L−1 of HCl solution containing 18.4 g L−1 of ammonia peroxydisulfate (Sigma-Aldrich) oxidant with a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. After stirring the mixture at 400 rad min−1 for 20 min, the PANI was separated by paper filtration, washed with water until a pH = 7 was reached and then dried in air overnight at 60 °C. Then, PANI was carbonized in a quartz tube furnace by pyrolysis under 100 mL min−1 Argon flow. The heating rate of the furnace was set at 20 °C min−1, and the maximum temperature (500 to 750 °C) was held for a 2 h dwell. The carbonized PANI was then milled with KOH pellets (Merck kGaA) with a mass ratio of 1
1. After stirring the mixture at 400 rad min−1 for 20 min, the PANI was separated by paper filtration, washed with water until a pH = 7 was reached and then dried in air overnight at 60 °C. Then, PANI was carbonized in a quartz tube furnace by pyrolysis under 100 mL min−1 Argon flow. The heating rate of the furnace was set at 20 °C min−1, and the maximum temperature (500 to 750 °C) was held for a 2 h dwell. The carbonized PANI was then milled with KOH pellets (Merck kGaA) with a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 in ethanol. The maximum activation temperatures applied varied from 700 to 850 °C. The heating rate was 10–20 °C min−1 and the maximum temperature was held at a dwell for 30, 60 or 120 min. After activation, the sample was washed with 1 mol L−1 HCl solution and distilled water until the pH remained constant at 7 and dried in air at 120 °C overnight. Further calcination was carried out to some of the samples for 12 h at 900 °C under argon. A CNS sample was also prepared by direct activation of the PANI with the exclusion of the carbonization step.
4 in ethanol. The maximum activation temperatures applied varied from 700 to 850 °C. The heating rate was 10–20 °C min−1 and the maximum temperature was held at a dwell for 30, 60 or 120 min. After activation, the sample was washed with 1 mol L−1 HCl solution and distilled water until the pH remained constant at 7 and dried in air at 120 °C overnight. Further calcination was carried out to some of the samples for 12 h at 900 °C under argon. A CNS sample was also prepared by direct activation of the PANI with the exclusion of the carbonization step.
Material characterization
The microstructure and morphology of the CNSs were characterized by scanning electron microscopy (S(T)EM, Hitachi S-5500) and high-resolution transmission electron microscopy (HR-TEM, Image Cs corrected JEOL ARM-200F). The BET surface area and the PSD were obtained from N2 sorption (−196 °C) and CO2 sorption (0 °C) isotherms performed on a Micromeritics Tristar II 3020 instrument. The samples were degassed at 200 °C for 12 h under turbomolecular vacuum pumping prior to the gas adsorption measurements. Raman spectroscopy (InVia Reflex Spectrometer System) with a 532 nm wavelength laser was used to analyse the disorder in the sample. X-ray photoelectron spectroscopy (XPS) analyses were carried using a Kratos Axis Ultra DLD spectrometer with a monochromatic AlKα radiation (hν = 1486.6 eV).Electrochemical measurements
The electrode active materials were prepared by milling the CNS powders with an 8 wt% polytetrafluoroethylene binder (PTFE solution, Sigma-Aldrich). The electrodes for the SCs were fabricated by pressing the CNS–PTFE mixture over a nickel foam disk (Alfa Acsar) at 6 MPa for a duration of 2 min. The mass loading of the active material was approximately 2 mg cm−2. The electrodes were dried in a vacuum oven at 120 °C overnight before assembling in an argon-filled glovebox.Two electrodes with the same mass loading were used to make a symmetric SC using a Split Test Cell (MTI, 20 mm). The electrolytes were neat ILs 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIMBF4) and 1-butyl-3-methylimidazolium hexafluorophosphate (BMIMPF6) (Sigma-Aldrich). The separator was a 25 μm thin microporous monolayer membrane (Celgard 3501) and 15 μL of electrolyte was added to each side of the separator. The prepared cells were stabilized overnight before the performance test.
The electrochemical performance of the SCs were evaluated by cyclic voltammetry (CV) and frequency response analysis on a Princeton VersaSTAT potentiostat analyser, as well as a galvanostatic charge/discharge test (GCD), a cycling stability test (1 A g−1) and a floating test on a MTI 8-channel battery analyser. The floating test was conducted as described by Ratajczak et al.,24 except that the highest voltage was fixed at 4 V in this work. Additionally, CNS1 was tested on a pilot-scale (Coffee-bag cell) at China Nantong Pilot-tests Institute of Green Technology. The CNS1–PTFE mixture was painted on a Ni plate current collector by a tape casting method with a CNS1 mass loading of 2.2 mg cm−2.
The gravimetric capacitance (or specific capacitance) of a single electrode was calculated from the GCD discharge curve according to:
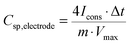 | (1) |
The specific energy and the average specific power of the cell were estimated:
 | (2) |
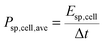 | (3) |
Results and discussion
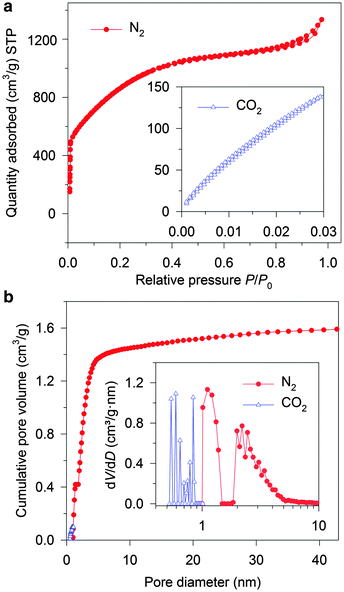
The SEM images of the typical CNS (CNS1) at medium (Fig. 1a) and low (Fig. S1b & c, ESI†) magnifications shows a homogenous sponge-like pore texture with hundred-nm-scaled three-dimensional (3D) distributed macropores, which demonstrated the difference between the CNSs and the typical ACs.20,25 Such a sponge-like structure with the average framework thickness of less than 100 nm (Fig. 1a) is expected to result in short ion diffusion distances (<50 nm) when the macropores are filled with the electrolyte.9 A highly porous character (Fig. 1b) of a large number of small pores with a pore size less than 10 nm can be observed on the framework, which is further proved by the HR-TEM image of the crushed CNS1 (Fig. 1c).These micro- and sub-mesopores are blind cylindrical, cone-shaped and/or wedge-shaped, as no clear hysteresis is observed in the N2 adsorption/desorption isotherms (at −196 °C) in Fig. 2a.26 On the TEM image (Fig. 1c) of the crushed CNS1, a loose and open nano-scale structure can be observed where the sample is thin (circled) at the edge of a pore wall. It seems to suggest a cylindrical-like pore structure with extremely thin walls. The PSD curve of the CNS1 derived from the N2 desorption isotherms using non-local density functional theory (NLDFT), assuming a cylindrical pore, shows a PSD with dual peaks (Fig. 2b inset), namely the micro- and sub-mesopores ranging from 1.0 to 1.4 nm and 1.8 to 6.0 nm, respectively. Additionally, the presence of some ultrafine micropores (<0.85 nm) is observed via DFT analysis of the CO2 sorption isotherm at 0 °C (Fig. 2b inset). For a material with a relatively broad PSD, the average pore size is not a comprehensive characteristic to correlate with the SC capacitance, unless the full range of PSD or at least the width of PSD is considered.13 The CNS materials with different PSDs (Table S1, ESI†) could be easily obtained by employing different carbonization and activation conditions, which allows the efficient selection of the samples with a similar PSD structure (dual-peaks and PSD widths) but different average pore sizes (Table S1, ESI†). The carbon chemistry is also considered in the carbon selection (Fig. S2, ESI†) as it was found to have impact on the capacitance.27 The selected CNSs (Table S1, ESI†) all exhibit impressive SSAs, a similar PSD structure and close crystallinity, making CNSs ideal candidates for studying the capacitance dependence on pore characteristics.
To study the pore size effect on the capacitance, the selected CNSs were used as electrode active materials for two-electrode symmetrical cells. Neat IL EMIMBF4 was chosen as the electrolyte as it provides a large voltage window and offers a well identified ion size without a solvation shell. Most of the pores in the selected CNSs were expected to be accessible to the electrolyte ions, as more than 89% (minimum among all the selected CNSs) of the total volume was contributed by pores larger than 1 nm for CNSs (Fig. 2b). In order to ensure the complete filling of the ion-assessable pores, and to approach the maximum discharge capacitance, the constant charge/discharge current density of 0.1 A g−1 was applied, since only minimal capacitance increase was found at a lower current density of 0.05 A g−1 (Fig. S3a, ESI†). Fig. 3 (marked by triangular dots) reveals a novel and complex trend of the gravimetric capacitance dependence on the average pore size. The gravimetric capacitance increased sharply by 138%, from 121 to 290 F g−1, as the average pore diameter increases from 1.9 nm to 2.3 nm, and then decreased to 220 F g−1 at the average pore size of 3.1 nm. Impressively, the downward trend of the capacitance does not show a continuous decrease, but swings in a capacitance range of ∼80 F g−1.
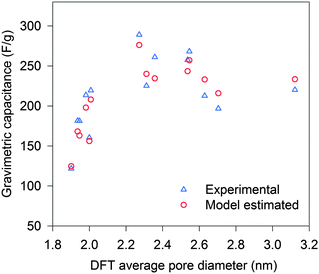 | ||
| Fig. 3 Gravimetric capacitance vs. DFT average pore diameter: experimental (triangle) and model estimated (circle). | ||
Initially, we used a traditional method of normalizing the gravimetric capacitance by ion-assessable SSA to analyze the effect of pore size irrespective of SSA. Fig. S4 (ESI†) shows a trend of increasing normalized capacitance, when the average pore size is reduced from 3.1 nm to 1.9 nm. This can be explained by the increasing ratio of micropores (D near 1.0 nm) which has been recognized to result in higher normalized capacitance.10,11 As the average pore sizes are larger than 1.9 nm, there are more mesopores than micropores in the CNSs. However, some of the normalized capacitances of the mesopore-rich CNSs were unexpectedly higher than that of the micropore-only carbon material which was recognized to have the highest normalized DL capacitance (≈13.5 μF cm−2) for the carbon material.11 This cannot be explained by the current understanding of the pore size effect. As the average pore size offers very limited information, a better understanding of the ion filling inside confined pores on the porous carbon is essential.
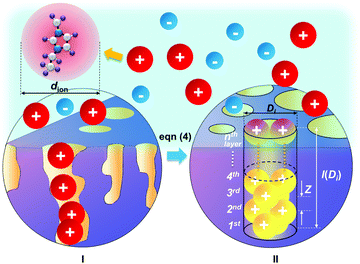
Since the cation EMIM+ is much larger than the anion BF4−, we focus on the cation-sorbed electrode (or the negatively charged electrode), which has a lower electrode capacitance compared to that of its counter electrode in a symmetrical two-electrode cell.28,29 The potential absolute value for the negatively charged electrode is about 2.0 V (defining the infinity is 0 V) in this work, only cations are adsorbed on the negatively charged surface based on the MD simulation performed by Kislenko et al.30 Moreover, only one (rather than two) monolayer of cations is considered to be tightly adsorbed on the surface of the electrode, as the potential absolute value of the electrode is lower than 2.6 V.31 For the imidazolium-type of cation BMIM+ adsorbed on the first layer of a negatively charged carbon surface, the reported distance from the cation ring to the charged surface (l0) and to the adjacent cation (li) are approximately 0.35 nm and 1.00 nm, respectively.30 As li > 2l0 ≥ cationic size, which are estimated by the van der Waals volumes of EMIM+ and BMIM+ to be 0.61 nm and 0.66 nm,32 respectively, the real geometric shape of the cations (EMIM+ and BMIM+) does not have a strong influence. Thus a cation BMIM+ near the electrode surface can be simplified into a sphere with an effective ion size of 1.00 nm based on the li,30 representing the occupation size of ion. The effective ion size (dion) of EMIM+ is estimated to be 0.97 nm, as it is 2 methylene units (0.03 nm) smaller in the alkyl substituent than BMIM+.
The pore structure of CNS was observed experimentally to be cylindrical as noted above. More realistically, the cylindrical-like pores are non-ideal with varying diameters and depth as shown in the Fig. 4I. On the purposes of theoretical modeling, we convert the cumulative pore volume curve (Fig. 2b) based on:
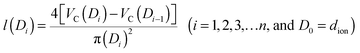 | (4) |
The DL capacitance of the material is determined by the total charge accumulated on the electrode, or more precisely the number of charged ions adsorbed on the surface of the pore with the given PSD. To maximize the number of ions distributing on the inner surface of the regular cylindrical pores, we assume that the ions are self-assembled to achieve the densest surface packing. The detailed ion packing configurations are given in the ESI,† and an example is given as Fig. 4II. Subsequently, we have derived a general formula to quantitatively evaluate the maximum number of ions adsorbed on the surface of the porous material, by summing up the number of ions stored on all the ion-accessible pores (D1 to Di from the PSD) of the sample (derivation see eqn (S1)–(S15), ESI†), finding:
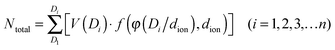 | (5) |
By taking into account the specific PSDs of CNSs, the gravimetric capacitances of the CNS materials listed in Table S1 (ESI†) were estimated based on our model. The estimated values are plotted with the average pore sizes in Fig. 3 (marked by circles). The estimated gravimetric capacitances show a high consistency with the experimental data. Moreover, the model was applied to other types of carbon materials (such as: AC, activated graphene and ordered mesoporous carbon) in the literature where both full-range PSDs and capacitances were reported. The model prediction again fits well with the experimental capacitances (Fig. S6, ESI†), which suggest that the model is valid for a wide range of carbon materials. Thus, the PSD-confined ion packing is the dominant factor that influences the capacitance. Further improvement in estimating the gravimetric capacitance could be achieved by taking the other influential factors, such as the “overscreening” effect, detailed carbon chemistry and applied voltage, into consideration.12,27,33
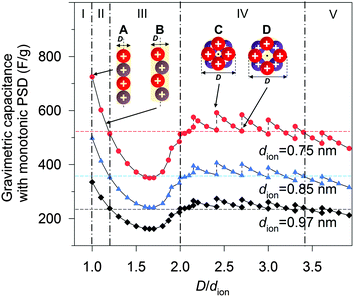
To shed light on the effect of ion-packing function, we extend eqn (5) further by assuming that the pores of the material are ideally mono-dispersed (monotonic PSD) with a fixed total pore volume. By further fixing the dion, the gravimetric capacitance is correlated solely by the volume fraction φ (eqn (S16), ESI†) or, more specifically, the pore volume (rather than the surface area) utilization by the ions (eqn (S12), ESI†). Fig. 5 shows the simulated gravimetric capacitances of the monotonic-PSD material with a total specific pore volume of 1.5 cm3 g−1 (similar to CNS1) as a function of the relative pore size (D/dion) at three given dions (0.75, 0.85 and 0.97 nm). Five regions are defined in Fig. 5, based on the changes of gravimetric capacitance with the D/dion ratio (above or below the horizontal dash lines), and the partition of regions is independent of the dion values. In region I (D/dion < 1.00), no ions can access the surface inside the pore, due the electrolyte ion size being larger than the pore size. A narrow capacitance-favourable region (region II), where the pore size is equal or a little larger than the ion size, was formed due to the high pore volume utilization of the ions as illustrated and indicated as schemes A and B in Fig. 5. When dion = 0.97 nm (estimated dion of EMIM+ at room temperature described above), our model predicted that the maximum capacitance is achieved with D = 0.97 nm, which is similar to the optimized pore size of 0.95 nm by a MD study of EMIM+ in cylindrical carbon micropores.15 It is also worth mentioning that the anomalous increases of the capacitance with the decreases of the D/dion ratio in the range of 1.00 ≤ D/dion < 1.70 is in good agreement with the experimental observation of Largeot et al.11 As the capacitance also increases sharply when the D/dion increases from 1.70 to 2.00, a ‘rock-bottom’ capacitance region III is formed. In region IV (2.00 ≤ D/dion < 3.40), there are five local maximum capacitances, corresponding to five densest-surface ion packing configurations when the pore size can exactly adapt the integer number (3, 4, 5, 6 or 7) of ions. The capacitance decreases concurrently with the increase in D/dion between these five particular situations, due to the decreases of the volume utilization fraction, and one example is illustrated as schemes C to D in Fig. 5. This explains the experimental observation of discontinuity in the pore size dependence of the capacitance in Fig. 3 well. It is also interesting to note that the capacitances did not vary very much in region IV compared to region II. At even larger relative pore sizes (region V, D/dion ≥ 3.40), the capacitances are generally lower than those in region IV.
According to eqn (5), there will be a beneficial ion packing with an enhanced capacitance when more specific pore volume is contributed by the pores falling in the capacitance-favourable regions II and IV in Fig. 5. Although the theoretical capacitance in region II is higher than that in region IV, it should be noted that it is still more beneficial to design PSD of the carbon–IL system close to region IV, where the capacitance is not so sensitive to PSD and thus could adapt for broader PSD. In addition, mesopores are favourable for fast ion transportation which gives good rate capability of SCs compared to the micropores.8 For example, the CNS1 contains more mesopores than micropores as the average pore size is 2.55 nm. Despite the relatively broad PSD of CNS1, the experimental capacitance is 268 F g−1, which is close to the second theoretical maximum capacitance (region IV of Fig. 5) of 273 F g−1 (dion,EMIM+ = 0.97 nm). That is due to the location of the PSD dual peaks close to both of the capacitance-favorite regions (II & IV) while away from the capacitance-detrimental region III. With more mesopores, the SC–CNS1 also gives a good rate capability as shown in the GCD curve (Fig. S3b, ESI†). Moreover, the cyclic voltammetry CV curve (Fig. S3c, ESI†) indicates a near-ideal capacitive behavior of the SC in a wide range of scan rates (50–300 mV s−1).
The ion-packing function suggests that the dion is another important parameter which can be adjusted in order to optimize the ion packing (Fig. 5). The decrease of dion results in enhanced capacitance for a given PSD, as more ions can be stored per unit volume of the ion-accessible nanopores. Unfortunately, suitable commercial ILs with variable ionic sizes are still very limited, and further developments of ILs with a small ionic size are highly desirable. Another strategy for tuning dion relies on the change of cell operation temperature.34,35 With increasing temperature, the decrease of distance from the absorbed ion to the charged surface was observed34 and the distance decreases between two adjacent ions can also be expected according to the definition of the Bjerrum length (details in the ESI†).35 Therefore, both experimental observations and theory suggest a smaller effective ion size at a higher temperature. In this regard, the performance of the supercapacitors was tested at high temperatures.
Indeed, the gravimetric capacitance of SC–CNS1 was boosted at elevated temperatures. The discharge capacitance of a single electrode in the EMIMBF4 and the BMIMPF6 electrolyte (0.5 A g−1) was up to 376 F g−1 (0–3.5 V) and 387 F g−1 (0–4 V) at 60 °C (Fig. S7a, ESI†). The effective ion size estimated by the ion-packing model decreases from 0.97 nm and 1.00 nm at 20 °C to 0.81 nm and 0.80 nm at 60 °C for EMIM+ and BMIM+, respectively, which suggests that the temperature possibly changes the dion and thus influences the capacitance. For the SC–CNS1 in the BMIMPF6 electrolyte, a voltage window of 0–4 V was applicable at 60 °C, since no obvious distortion of the CV curve was observed (Fig. S7b, ESI†). The high gravimetric capacitance (60 °C) with a large discharge voltage in BMIMPF6 results in an unprecedented specific energy of 204 W h kg−1 (based on the mass of the active material), which is slightly lower than the theoretical specific energy of nickel–cadmium (NiCd) batteries (220 W h kg−1).5 As the typical weight ratio for the active electrode material in a packaged SCs is around 30%,36 the practical specific energy for packaged SCs at 60 °C is expected to be 61.3 W h kg−1, which is comparable with the NiMH battery (60–100 W h kg−1).1 At the identical specific energy, the CNS1–SC has the advantage of higher power density, which is more than one order of magnitude higher than the NiMH batteries (Fig. 6). The SC also delivered a good long-term cycling stability at both 20 °C and 60 °C as shown in Fig. 7. The frequency response analysis (yields the Nyquist plot), the floating test result (constant voltage hold test) and the pilot-scale test result are provided for completeness in the ESI† (Fig. S7c–f).
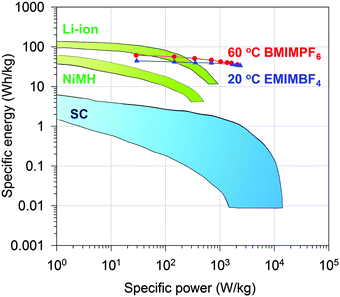 | ||
| Fig. 6 Ragone plot of specific energy vs. specific power for packaged CNS1–SC and other state-of-art energy storage devices.1 | ||
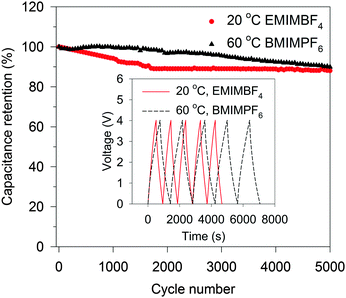 | ||
| Fig. 7 Cycling stability of CNS1–SC at 1.0 A g−1 for 5000 cycles of charge–discharge. The inset shows five cycles of charge–discharge. | ||
Conclusions
We have developed a model describing the geometrically confined ion packing configuration in micro- and meso-cylindrical pores, which is based on the densest surface packing. Exploiting the PSDs of large-SSA, mesopore-rich and sponge-like CNSs and literature-reported carbon materials, the model-estimated capacitances agree well quantitatively with experimental results. We show that the gravimetric capacitance in cylindrical nanopores is essentially determined by the correlation between the ion-packing function and the geometric factors (PSD and effective ion size) of the material and the electrolyte. As the desired PSD of CNS corresponds to favourable ion-packing according to our model, the highest DL capacitance in this work is 290 F g−1, which is among one of the highest recorded DL capacitance.17 With the decreased effective ion size at 60 °C, the gravimetric capacitance of CNS electrodes improved dramatically, to 387 F g−1 with a high discharge voltage of 4 V, good rate capability and cycling stability. This work radically improves our ability for rational design of various carbon materials and ILs, and opens up great possibility of developing a new generation of SCs which could provide both high specific energy and specific power.Acknowledgements
We acknowledge funding from Research Council of Norway (project 10388902 and NorFab 197411/V30). We thank F. Béguin at Poznan University of Science and Technology for helpful discussion. We thank M. E. M. Buan at Norwegian University of Science and Technology for help in XPS experiments. We also thank China Nantong Pilot-tests Institute of Green Technology for helping to fabricate and test the coffee-bag cells.Notes and references
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- J. R. Miller, Science, 2012, 335, 1312–1313 CrossRef CAS PubMed.
- A. S. Arico, P. Bruce, B. Scrosati, J.-M. Tarascon and W. Van Schalkwijk, Nat. Mater., 2005, 4, 366–377 CrossRef CAS PubMed.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed.
- M. Winter and R. J. Brodd, Chem. Rev., 2004, 104, 4245–4270 CrossRef CAS PubMed.
- T. Kim, G. Jung, S. Yoo, K. S. Suh and R. S. Ruoff, ACS Nano, 2013, 7, 6899–6905 CrossRef CAS PubMed.
- F. Huang and D. Chen, Energy Environ. Sci., 2012, 5, 5833–5841 CAS.
- L. L. Zhang and X. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- D. W. Wang, F. Li, M. Liu, G. Q. Lu and H. M. Cheng, Angew. Chem., 2008, 120, 379–382 CrossRef.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P.-L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- S. Kondrat, C. Perez, V. Presser, Y. Gogotsi and A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 CAS.
- J. Huang, B. G. Sumpter and V. Meunier, Angew. Chem., Int. Ed., 2008, 47, 520–524 CrossRef CAS PubMed.
- Y. Shim and H. J. Kim, ACS Nano, 2010, 4, 2345–2355 CrossRef CAS PubMed.
- F. B. Sillars, S. I. Fletcher, M. Mirzaeian and P. J. Hall, Energy Environ. Sci., 2011, 4, 695–706 CAS.
- Y. Xu, Z. Lin, X. Zhong, X. Huang, N. O. Weiss, Y. Huang and X. Duan, Nat. Commun., 2014, 5, 4554 CAS.
- F. Bonaccorso, L. Colombo, G. Yu, M. Stoller, V. Tozzini, A. C. Ferrari, R. S. Ruoff and V. Pellegrini, Science, 2015, 347, 1246501 CrossRef PubMed.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC.
- J. Wang and S. Kaskel, J. Mater. Chem., 2012, 22, 23710–23725 RSC.
- T.-Y. Ma, L. Liu and Z.-Y. Yuan, Chem. Soc. Rev., 2013, 42, 3977–4003 RSC.
- Z. Lei, N. Christov and X. Zhao, Energy Environ. Sci., 2011, 4, 1866–1873 CAS.
- J. Huang and R. B. Kaner, Angew. Chem., 2004, 116, 5941–5945 CrossRef.
- P. Ratajczak, K. Jurewicz and F. Béguin, J. Appl. Electrochem., 2014, 44, 475–480 CrossRef CAS.
- L. Wei, M. Sevilla, A. B. Fuertes, R. Mokaya and G. Yushin, Adv. Funct. Mater., 2012, 22, 827–834 CrossRef CAS.
- K. S. Sing, Pure Appl. Chem., 1985, 57, 603–619 CrossRef CAS.
- M. Deschamps, E. Gilbert, P. Azais, E. Raymundo-Piñero, M. R. Ammar, P. Simon, D. Massiot and F. Béguin, Nat. Mater., 2013, 12, 351–358 CrossRef CAS PubMed.
- A. A. Kornyshev and L.-P. Yang, Electrochem. Commun., 2014, 48, 173–177 CrossRef CAS.
- C. Ania, J. Pernak, F. Stefaniak, E. Raymundo-Pinero and F. Beguin, Carbon, 2006, 44, 3126–3130 CrossRef CAS.
- S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590 RSC.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- H. Tokuda, K. Ishii, M. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833–2839 CrossRef CAS PubMed.
- M. Mirzadeh, F. Gibou and T. M. Squires, Phys. Rev. Lett., 2014, 113, 097701 CrossRef PubMed.
- M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. M. Ocko and J. Ralston, Science, 2008, 322, 424–428 CrossRef CAS PubMed.
- N. I. Lebovka, in Polyelectrolyte Complexes in the Dispersed and Solid State I, ed. M. Müller, Springer, Dresden, 2014, pp. 57–96 Search PubMed.
- Y. Zhu, S. Murali, M. D. Stoller, K. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz and M. Thommes, Science, 2011, 332, 1537–1541 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SEM images, XPS and Raman characterization, electrochemical measurement and model derivations. See DOI: 10.1039/c5ee02702k |
| This journal is © The Royal Society of Chemistry 2016 |