Open Access Article
Open Access ArticleAn electrochemical engineering assessment of the operational conditions and constraints for solar-driven water-splitting systems at near-neutral pH†
Meenesh R.
Singh
 a,
Kimberly
Papadantonakis
b,
Chengxiang
Xiang
*b and
Nathan S.
Lewis
*bc
a,
Kimberly
Papadantonakis
b,
Chengxiang
Xiang
*b and
Nathan S.
Lewis
*bc
aJoint Center for Artificial Photosynthesis, Lawrence Berkeley National Laboratory, Berkeley CA 94720, USA
bJoint Center for Artificial Photosynthesis, California Institute of Technology, Pasadena CA 91125, USA. E-mail: cxx@caltech.edu; nslewis@caltech.edu
cDivision of Chemistry and Chemical Engineering, California Institute of Technology, 210 Noyes Laboratory, 127-72, Pasadena, CA 91125, USA
First published on 30th June 2015
Abstract
The solution transport losses in a one-dimensional solar-driven water-splitting cell that operates in either concentrated acid, dilute acid, or buffered near-neutral pH electrolytes have been evaluated using a mathematical model that accounts for diffusion, migration and convective transport, as well as for bulk electrochemical reactions in the electrolyte. The Ohmic resistance loss, the Nernstian potential loss associated with pH gradients at the surface of the electrode, and electrodialysis in different electrolytes were assessed quantitatively in a stagnant cell as well as in a bubble-convected cell, in which convective mixing occurred due to product-gas evolution. In a stagnant cell that did not have convective mixing, small limiting current densities (<3 mA cm−2) and significant polarization losses derived from pH gradients were present in dilute acid as well as in near-neutral pH buffered electrolytes. In contrast, bubble-convected cells exhibited a significant increase in the limiting current density, and a significant reduction of the concentration overpotentials. In a bubble-convected cell, minimal solution transport losses were present in membrane-free cells, in either buffered electrolytes or in unbuffered solutions with pH ≤ 1. However, membrane-free cells lack a mechanism for product-gas separation, presenting significant practical and engineering impediments to the deployment of such systems. To produce an intrinsically safe cell, an ion-exchange membrane was incorporated into the cell. The accompanying solution losses, especially the pH gradients at the electrode surfaces, were modeled and simulated for such a system. Hence this work describes the general conditions under which intrinsically safe, efficient solar-driven water-splitting cells can be operated.
Broader contextContact with strongly acidic or alkaline electrolytes presents significant challenges to the stability of some prospective catalysts and light absorbers, particularly when rare elements are not utilized in the system. Considerable efforts are being directed toward systems that employ electrolytes with neutral or near-neutral pH values to circumvent the materials stability challenge. To develop an efficient, intrinsically safe, and scalable solar-driven water-splitting system that operates at near-neutral pH, the rates of gas crossover, concentration-overpotential losses, electrolyte resistive losses, and electrodialysis processes must be minimized simultaneously. While some studies have shown unassisted solar-driven water-splitting in a membrane-free cell, an efficient and intrinsically safe cell that provides robust gas collection and separation has yet to be demonstrated at near-neutral pH conditions. Herein we have evaluated quantitatively, using mathematical modeling, the various loss mechanisms and safety considerations involved in a one-dimensional (1-D) solar-driven water-splitting system that operates either in concentrated acid, dilute acid or buffered electrolytes at near-neutral pH, with or without membrane separators. |
1. Introduction
An efficient, stable, and scalable artificial photosynthetic system could provide a sustainable carbon-neutral source of fuels.1 Solar-driven water-splitting devices, based on a variety of designs that incorporate varying levels of integration, and using a variety of materials, have been demonstrated experimentally,2–11 and several generic system designs have been modeled and simulated in detail.12–20 In typical electrolyzers or fuel cells, strongly acidic or alkaline electrolytes, with high ionic conductivities (such as 1 M H2SO4 or 1 M KOH) and unity transference numbers for protons or hydroxide ions, are used to minimize the resistive losses and concentration overpotentials in the system.21 Modeling and simulation efforts have similarly shown that strongly acidic or alkaline electrolytes with high ionic conductivities and high proton/hydroxide transference numbers are needed for maximally efficient operation of an intrinsically safe solar-driven water-splitting system.16,17 Optimized system designs that include membranes for the separation of products can produce combined solution and membrane-transport losses of <100 mV at operating current densities, J, of >20 mA cm−2, i.e. with solar-to-hydrogen efficiencies in excess of 24%.16,17Contact with strongly acidic or alkaline electrolytes presents significant challenges to the stability of some prospective catalysts and light absorbers, particularly when rare elements (such as Ir) are not utilized in the system, to minimize the materials cost and improve the potential system scalability.22–24 Many technologically important semiconductors (such as Si, GaAs, CdTe, and InP) are unstable in either strong acid or strong base, and to date only catalysts derived from noble metals exhibit active and stable electrocatalysis of the oxygen-evolution reaction (OER) in strong acid.25 Considerable efforts are being directed toward the discovery and development of new earth-abundant light absorbers and electrocatalysts that will be stable under such conditions, whereas other efforts have been directed toward systems that employ electrolytes with neutral or near-neutral pH values.6,26–28 Solar-driven water-splitting devices consisting of a set of discrete photovoltaic cells connected electrically in series with a separate two-electrode electrolysis cell operated using electrolytes with near-neutral pH values have demonstrated solar-to-hydrogen efficiencies as high as 10%.6 However, such systems lack a mechanism for separation of the products, and thus are not intrinsically safe because co-evolved, stoichiometric mixtures of H2(g) and O2(g) are produced. Moreover, the incorporation of membranes, to provide for robust product separation in such near-neutral pH solar-to-hydrogen systems, yields large reductions in the system efficiency and also produces significant pH gradients near the electrode surfaces, subjecting the electrodes to increasingly corrosive local environments and typically changing the chemical form of the electrocatalysts to reflect the change in the local pH near the electrode surface.27
To develop an efficient, intrinsically safe, and scalable solar-driven water-splitting system that operates at near-neutral pH, the rates of gas crossover, concentration-overpotential losses, electrolyte resistive losses, and electrodialysis processes must be minimized simultaneously. The trade-offs between the efficiency of the device and the product-gas crossover in a membrane-based and a membrane-free solar-driven water-splitting system have been evaluated experimentally for operation using a buffered electrolyte.27 The membrane-free device exhibited significant product-gas crossover, with 10% O2(g) found in the cathode chamber and up to 40% H2(g) measured in the anode chamber.27 An accompanying modeling analysis showed that an integrated system operating at a current density of 2.5 mA cm−2 with an electrolyte buffered at pH = 9.2 would locally produce pH > 13 at the photocathode and locally produce pH ≤ 7 at the photoanode, in addition to producing a severe reduction in the system efficiency.27
Such changes in the near-electrode pH that accompany electrolysis in a full system thus confound a strategy of utilizing electrolytes with neutral or near-neutral bulk pH values to relax the requirements for materials stability. Moreover, almost all near-neutral pH devices constructed to date lack a membrane separator that can facilitate transport of buffer ions between the cathode and anode chamber. The lack of a mechanism to prevent the diffusive and convective product-gas crossovers, especially in monolithically integrated solar–hydrogen devices, where the rate of product-gas evolution would be highly non-uniform both spatially and temporally, would present significant safety concerns for deployment of such devices at large scale. Herein we have evaluated quantitatively, using mathematical modeling, the various loss mechanisms and safety considerations involved in a one-dimensional (1-D) solar-driven water-splitting system that operates either in concentrated acid, dilute acid or buffered electrolytes at near-neutral pH, with or without membrane separators. We first describe the 1-D mathematical model for the transport of ionic, neutral, and buffer species in the electrolyte. We then describe the use of the model to explore the effects of the initial electrolyte pH, the convective mixing in the cell, the concentrations and types of buffered species in the electrolyte, and the use of ion-exchange membranes, as well as to understand the operational near-electrode pH values and voltages needed to drive the water-splitting reaction at specific current densities in such systems.
2. Modeling
2.1 Cell design
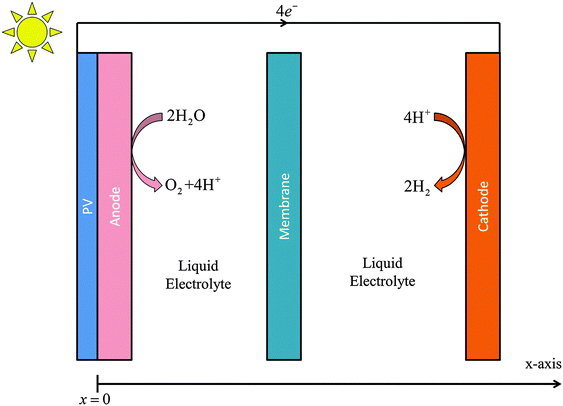
Fig. 1 illustrates the one-dimensional (1-D) simplified, planar model of a photoelectrochemical cell that was used to analyze the transport of species in the electrolyte, as well as to evaluate the effect of electrolyte composition on the distribution of the potential losses in such systems. The cathode and anode were separated by 1 cm. The current density vs. potential characteristics of IrOx and Pt in acid that were fitted by a Bulter–Volmer relation were used for the anode and cathode, respectively. The transport loss in the system is not dependent on the detailed electrocatalytic parameters of the cathode and anode, but is only a function of the operating current density at the electrode surfaces. The physical properties and parameters used in the simulations are tabulated in the ESI.†2.2 Solution transport in the electrolyte and in the membrane separator
Established electrochemical relationships, specifically, the Nernst–Planck equation, were used to describe the flux of species in the electrolyte including diffusion, migration, convection and bulk reactions of water or buffer dissociation.29 Ionic species (protons, hydroxides, co-cations and co-anions) and neutral species (water, buffer, and dissolved gases) were included in the model.In one set of simulations, the electrolyte in the photoelectrochemical cell was assumed to be stagnant (i.e., without convective flow). A boundary layer thickness of 2 mm was used in the stagnant cell. For comparison, in the other set of simulations, convective forces were introduced by allowing for the evolution of bubbles from the electrode surfaces. This process resulted in a circulatory flow pattern in the electrolyte that determined the thickness of the boundary layer at the electrode surface.30 Effective diffusion coefficients for solution species were employed beyond the hydrodynamic boundary layer in the bulk solution to account for the convective forces in the cell. The detailed calculation of the effective diffusion coefficient based on the solution velocity perpendicular to the electrode surface and the tabulated values can be found in the ESI.† For the bubble-convected cell, the boundary-layer thickness decreased as the operating current density increased. A weak dependence of the measured boundary-layer thickness on the operating current density was observed due to the bubble evolution close to the electrode surface. Moreover, the potential loss at lower current densities was not significant. Hence, a boundary-layer thickness of 50 μm at the electrode surfaces, with the corresponding spatially averaged current density of ∼10 mA cm−2, was assumed in the calculation.30
The bubble-covered electrode surface during HER or OER resulted in a decrease of the active catalyst area and an increase of the kinetic overpotential. Increasing the bubble-coverage area on the electrodes can also increase the mixing in the electrolyte. The percentage coverage of bubbles on electrodes were 5%, 10%, and 20% for normalized current densities of 1 mA cm−2, 10 mA cm−2, and 100 mA cm−2, respectively.31 A 10% bubble coverage that corresponds to the current density of 10 mA cm−2 was used to calculate the average velocity of electrolyte perpendicular to the electrode. Increasing the bubble coverage area to 10% will reduce the exchange-current density in the Butler–Volmer expression by 10%, which does not have a significant effect on the kinetic overpotential. Moreover, the additional kinetic overpotential loss due to the increased bubble coverage at the electrode surface does not affect other solution transport losses in the calculation.
In the simulation of membrane-based cells, the anion-exchange membrane (AEM) was modeled as having diffusion coefficients of anions and cations that were 10−1 and 10−2 lower, respectively, than the corresponding values in the bulk solution. For the cation-exchange membrane (CEM), the diffusion coefficients of anions and cations were modelled as 10−2 and 10−1 lower, respectively, than their corresponding values in the bulk solution. A fixed background charge was assumed in the ion-exchange membranes.
2.3 Governing relations for polarization losses
The total voltage requirement (Δϕcell) for an electrochemical cell is the sum of the equilibrium potential (E0), kinetic overpotentials (η), solution losses (Δϕsolution), and the Nernstian losses associated with pH gradients at the surface of the electrodes (ΔϕpH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradients):
gradients):Δϕcell = E0 + ηOER − ηHER + Δϕsolution + ΔϕpH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradients gradients | (1) |
The solution losses, (Δϕsolution), are the sum of the Ohmic resistance loss (first term) and the electrodialysis loss (second term). These losses can be expressed as:
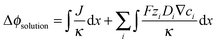 | (2) |
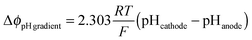 | (3) |
3. Results
3.1 Stagnant or bubble-convected membrane-free cells with dilute acid electrolytes
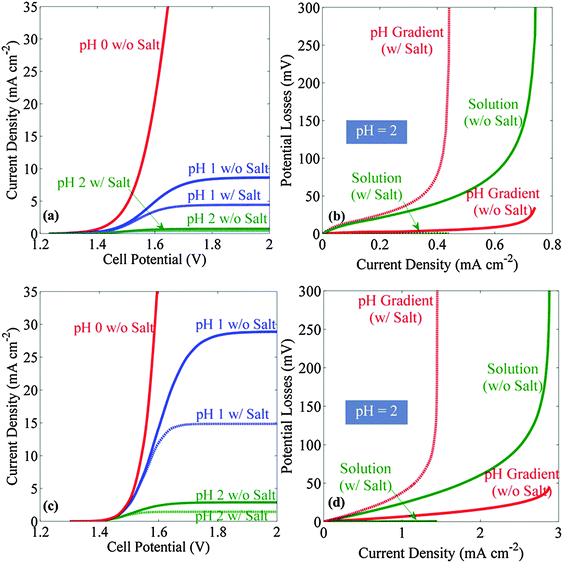
Fig. 2 shows the current–density versus voltage (J–V) behavior, and the accompanying potential losses as a function of current density, for a stagnant membrane-free system (Fig. 2a and b) as well as for a bubble-convected membrane-free system (Fig. 2c and d), when both systems were operated in dilute acid, with or without supporting electrolyte. The current density increased monotonically with increase in the applied voltage until a limiting value, i.e. a plateau, was reached (Fig. 2a and c). Both the limiting current density and the slope of the J–V characteristic decreased as the pH of the electrolyte increased. In the 1-dimensional cell configuration considered herein, the convective flux induced by bubble evolution at the electrode surfaces resulted in effective mixing of the electrolyte between the cathode and anode, and yielded increases in the operational current densities at a given applied potential, relative to the behavior in stagnant electrolytes. When a supporting electrolyte was added to the solution, the limiting current densities decreased in all cases, due to the reduction of the migration force caused by screening of electric field. For all solutions with pH > 1, the limiting current densities were <10 mA cm−2, regardless of whether the system was stagnant or experienced convection by bubbles. Hence, such simple dilute acid electrolytes do not allow for the construction of efficient solar-driven water-splitting systems in this electrode geometry.Fig. 2b shows the transport losses in a pH = 2 solution as a function of the operating current density, in a stagnant cell with or without supporting electrolyte, respectively. Without a supporting electrolyte (solid lines), at high current densities the Ohmic resistance loss (green solid line) dominated the transport loss. Addition of the supporting electrolyte minimized the Ohmic resistance loss (dotted green line), but increased the concentration overpotential associated with the pH gradients at the electrode surface (dotted red line), due to the reduced proton-migration force in the solution. Hence, a lower limiting current density was observed in solutions that contained supporting electrolyte than in those that did not contain added salt. Similar behavior was also observed for the transport losses in bubble-convected systems (Fig. 2d).
3.2 Stagnant or bubble-convected membrane-free cells with electrolytes buffered to near-neutral pH values
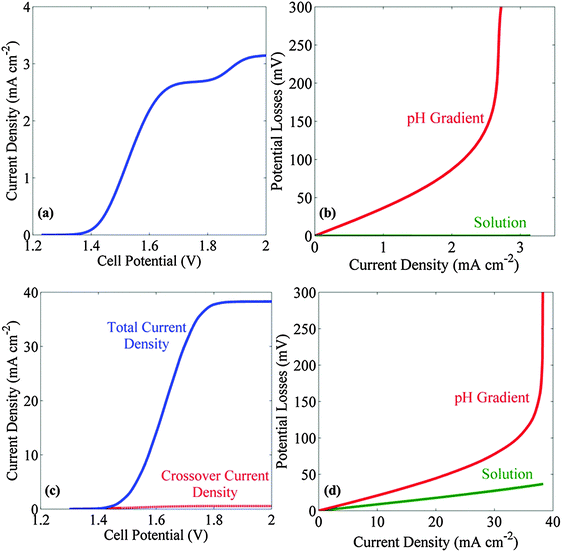
Fig. 3a and c show the J–V behavior in a stagnant and bubble-convected cell, respectively, with the 1.0 M electrolyte buffered at pH = 7. The limiting current densities were 3.2 mA cm−2 for the stagnant cell and 38 mA cm−2 for the bubble-convected cell, respectively. The cause of the two plateaus observed in the J–V characteristics in a stagnant cell is discussed in the ESI.† The ESI† also includes an analysis of the partial current density and of the concentration distribution of different ionic species. The effects of buffering the electrolyte at a pH not equal to the pKa of the buffer are also discussed in ESI.† Due to the low solubility of the product gases, the crossover current density (dotted black curve in Fig. 3c) (due to hydrogen oxidation at the anode or due to oxygen reduction at the cathode) was <1 mA cm−2 in the bubble-convected cell. Fig. 3b and d show the transport losses in a stagnant electrolyte and in the bubble-convected cell, respectively, when the electrolyte was buffered at pH = 7. At 10 mA cm−2 of operating current density, the total transport loss in a bubble-convected cell was <30 mV. The cases wherein the conjugate acid in the buffer pair is a negatively charged species are specifically relevant to electrolytes buffered with phosphate (pKa 7.21), carbonate (pKa 10.25), and borate (pKa 9.23), and the corresponding results for such systems are shown in the ESI.†3.3 Membrane-containing cells with electrolytes buffered at near-neutral pH
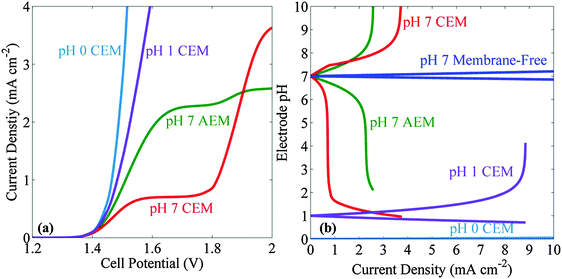
Fig. 4a shows the J–V behavior for an electrolyte buffered at pH = 7 in a system that also contained a 100 μm thick ion-exchange membrane to separate the product gases. The transport of ionic species between the cathode and anode was limited by the transport across the membrane. Relative to the stagnant membrane-free case, the introduction of the AEM or CEM lowered the current density of both systems. Hence, even in the bubble-convected cell, the limiting current density was <3.7 mA cm−2 in a system that used an AEM or CEM. For the CEM, the current densities at low voltages were much less than those for the AEM cells. In contrast, at higher applied potentials, the CEM-containing cell out-performed both of the AEM systems and also exhibited a higher limiting current density than the AEM systems. Other buffered systems, including phosphate, carbonate and borate buffers were also investigated in the membrane-based cells. Small limiting current densities (<2 mA cm−2) were observed in all cases, even with bubble-induced convective mixing (see ESI†). In addition, the J–V behavior of the acidic electrolyte in a membrane-containing cell was compared with the one in the neutral pH system. Fig. 4a shows that the neutral pH membrane-containing cell has an additional voltage loss of 350 mV at a current density of 2.5 mA cm−2 as compared to the pH = 0 electrolyte membrane-containing cells.Fig. 4b presents the pH at the electrode surface as a function of the operating current density, for membrane-free and membrane-containing cells, respectively. Significant pH gradients were observed in the neutral pH membrane-containing cells, even at operating current densities of <3 mA cm−2. Negligible pH changes were observed in pH 0 electrolytes and significant pH changes were observed for the pH 1 electrolytes at current densities >8 mA cm−2.
4. Discussion
4.1 Electrolyte constraints for efficient and intrinsically safe systems
To be deployed commercially, electrolyzers must be intrinsically safe, which means that the operational unit cannot result in the production of flammable mixtures of H2(g)/O2(g) at any point in space or time. Because the stoichiometry of the evolved gases is 2H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1O2, a pressure differential will exist between the anolyte and catholyte in any system that facilitates beneficial collection of the H2(g). By Darcy's law, any significant, sustained pressure differential will force fluid from one compartment to the other, eventually leading to catastrophic failure of the system. Hence membranes or separators are integral components of commercial electrolyzer systems. Modern membrane-electrode assemblies (MEA) for use in compact electrolyzers are only efficient and viable in acidic or alkaline media, because protons or hydroxide ions must traverse the membrane to provide charge balance, while neutralizing the pH gradient that would otherwise develop as a result of local acidification of the electrolyte near the anode (while it is producing O2 and thus liberating protons), and local increases in the pH of the electrolyte near the cathode (while it is consuming protons in conjunction with evolution of H2 from water). At near-neutral pH, in the presence of buffers or salts that are needed to provide acceptable conductivity and thus tolerable Ohmic resistance losses, the transference number of the salt far exceeds that of the protons or hydroxide ions, whose concentrations are obviously minimal at near-neutral pH. Hence instead of neutralizing the pH gradient, two concentration gradients are produced, one due to protons and the other due to buffer counter ions that have been driven by migration, in a process called electrodialysis, across the membrane. Note that although either passive or forced convective mixing can establish a steady-state concentration profile in such a system, convection cannot eliminate the local concentration gradient nor the Ohmic resistance losses, and will serve to increase the gas crossover and vulnerability to pressure differentials that the membrane was designed to prevent.
1O2, a pressure differential will exist between the anolyte and catholyte in any system that facilitates beneficial collection of the H2(g). By Darcy's law, any significant, sustained pressure differential will force fluid from one compartment to the other, eventually leading to catastrophic failure of the system. Hence membranes or separators are integral components of commercial electrolyzer systems. Modern membrane-electrode assemblies (MEA) for use in compact electrolyzers are only efficient and viable in acidic or alkaline media, because protons or hydroxide ions must traverse the membrane to provide charge balance, while neutralizing the pH gradient that would otherwise develop as a result of local acidification of the electrolyte near the anode (while it is producing O2 and thus liberating protons), and local increases in the pH of the electrolyte near the cathode (while it is consuming protons in conjunction with evolution of H2 from water). At near-neutral pH, in the presence of buffers or salts that are needed to provide acceptable conductivity and thus tolerable Ohmic resistance losses, the transference number of the salt far exceeds that of the protons or hydroxide ions, whose concentrations are obviously minimal at near-neutral pH. Hence instead of neutralizing the pH gradient, two concentration gradients are produced, one due to protons and the other due to buffer counter ions that have been driven by migration, in a process called electrodialysis, across the membrane. Note that although either passive or forced convective mixing can establish a steady-state concentration profile in such a system, convection cannot eliminate the local concentration gradient nor the Ohmic resistance losses, and will serve to increase the gas crossover and vulnerability to pressure differentials that the membrane was designed to prevent.
The same principles can be reasonably applied as mandatory design criteria for a deployable solar-driven water-splitting system, whether the system is fully integrated or is instead comprised of a discrete electrolyzer connected to a discrete photovoltaic cell or module. Moreover, for efficient cell operation, the operating electrolysis current densities need to exceed 10 mA cm−2 while solution transport losses are minimized. As shown in Fig. 2, concentrated acids allow for such conditions to be met either in stagnant or in bubble-convected cells, but in the absence of a membrane such systems do not allow for robust product separation and thus are not intrinsically safe. Stagnant systems in the dilute electrolytes or in the buffered electrolyte systems that did not contain a membrane are inefficient and only yield small limiting current densities. In contrast, bubble-induced convection in the dilute electrolytes or in the buffered electrolyte systems significantly reduces the concentration-overpotential loss associated with pH gradients at the electrode surfaces. Hence such systems produce minimal solution transport losses in either buffered electrolytes or in unbuffered solutions with pH ≤ 1. However, such systems are not intrinsically safe because the bubble-induced convection produces stoichiometric mixtures of H2 and O2 in the presence of active catalysts for the recombination of these gases.
When a membrane is introduced in such systems, both to separate the product gases and to hold back pressure differentials between the anolyte and catholyte to thereby allow for beneficial collection of the H2 into a pipeline, significant potential losses are produced from the resulting pH gradients at the electrode surfaces, in both buffered and unbuffered electrolytes. Even at very low operating current densities (∼1 mA cm−2), more than 6 units of pH difference are produced in cells that contain a CEM (Fig. 4b). Consistently, the resulting concentration overpotentials have been observed experimentally to lead to an operational shut-down at steady-state of such membrane-containing solar-driven water-splitting cells that are operated in electrolytes buffered in the bulk to near-neutral pH values.27
4.2 Extension to 2-D systems
In a two-dimensional (2-D), back-to-back cell configuration based on a planar, impermeable tandem- or triple-junction semiconductor device,3,17,28 the ionic transport between the cathode surface and the anode surface must occur around the edges of the light-absorbing material. The electrochemical engineering-design principles of this type of system have been assessed in detail previously.17 If the lateral electrode dimensions in the 2-D cell are sufficiently large, convection due to bubbles will produce improved mixing in the electrolyte along lamella parallel to the electrode surface, but will not eliminate pH gradients or other concentration gradients that are produced in the direction perpendicular to the electrode surfaces. Convection will also not significantly affect the Ohmic resistance losses in the cell. Convection through gaps either in the material or around the edges of a finite-sized material will decrease the concentration gradients in the electrolyte perpendicular to the electrode surfaces and will thus reduce the associated potential losses, while however increasing the crossover of products and thus sacrificing intrinsic safety in the system.If instead a membrane is inserted into the restricted ionic pathways in the 2-dimensional, back-to-back cell configuration, a large concentration overpotential will develop, and the cell will cease operation, regardless of whether the electrolyte is stagnant or is experiencing convection due to bubble formation.27 As shown in Fig. 4, convection on either side of the membrane does not significantly affect transport through the membrane, which occurs predominantly by diffusion. Hence if a membrane is introduced, to maintain intrinsic safety of the system, the operational performance of such near-neutral buffered pH electrolysis cells will be deleteriously affected and only low solar-to-hydrogen conversion efficiencies will be observed at steady-state.
5. Conclusions
In concentrated acid (pH = 0), minimal solution transport loss (<2 mV) at an operational current density of 10 mA cm−2 was obtained with, or without, convective mixing in the cell. Low limiting current densities (<3 mA cm−2) in the dilute acid as well as in electrolytes buffered at near-neutral pHs were observed in the stagnant cell without any convective mixing. Bubble-induced convective mixing in the cell significantly reduced the concentration-overpotential losses associated with the development of pH gradients at the electrode surfaces. As a result, minimal solution transport losses (<25 mV at 10 mA cm−2) were present in either buffered electrolytes or in unbuffered solutions with pH ≤ 1 in bubble-convected, membrane-free cells. Although the membrane-free cell facilitated the transport of buffer solution through convective mixing, the lack of a mechanism for safe and robust collection of product gases could cause potential catastrophic failure of the system and results in a lack of intrinsic safety for such types of electrolysis units. When a membrane separator was used to prevent product gas crossover, significant Nernstian potential losses associated with large pH gradients (more than 6 pH units) at the surface of the electrodes were observed in the simulation, even at low operating current densities (∼1 mA cm−2). Hence, regardless of the behavior of the electrocatalysts themselves, electrolysis or photoelectrolysis in solutions buffered in the bulk to near-neutral pH is inefficient and/or not intrinsically safe.Acknowledgements
This material is based on work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award number DE-SC0004993.References
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS.
- S. Y. Reece, J. A. Hamel, K. Sung, T. D. Jarvi, A. J. Esswein, J. J. H. Pijpers and D. G. Nocera, Science, 2011, 334, 645–648 CrossRef CAS PubMed.
- G. Peharz, F. Dimroth and U. Wittstadt, Int. J. Hydrogen Energy, 2007, 32, 3248–3252 CrossRef CAS PubMed.
- J. W. Ager III, M. Shaner, K. Walczak, I. D. Sharp and S. Ardo, Energy Environ. Sci., 2015 10.1039/C5EE00457H.
- C. R. Cox, J. Z. Lee, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14057–14061 CrossRef CAS PubMed.
- K. Fujii, S. Nakamura, M. Sugiyama, K. Watanabe, B. Bagheri and Y. Nakano, Int. J. Hydrogen Energy, 2013, 38, 14424–14432 CrossRef CAS PubMed.
- T. J. Jacobsson, V. Fjallstrom, M. Sahlberg, M. Edoff and T. Edvinsson, Energy Environ. Sci., 2013, 6, 3676–3683 CAS.
- O. Khaselev, A. Bansal and J. A. Turner, Int. J. Hydrogen Energy, 2001, 26, 127–132 CrossRef CAS.
- S. Licht, B. Wang, S. Mukerji, T. Soga, M. Umeno and H. Tributsch, J. Phys. Chem. B, 2000, 104, 8920–8924 CrossRef CAS.
- J. Luo, J.-H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N.-G. Park, S. D. Tilley, H. J. Fan and M. Grätzel, Science, 2014, 345, 1593–1596 CrossRef CAS PubMed.
- J. R. Bolton, S. J. Strickler and J. S. Connolly, Nature, 1985, 316, 495–500 CrossRef CAS PubMed.
- H. Döscher, J. Geisz, T. Deutsch and J. Turner, Energy Environ. Sci., 2014, 7, 2951–2956 Search PubMed.
- L. C. Seitz, Z. B. Chen, A. J. Forman, B. A. Pinaud, J. D. Benck and T. F. Jaramillo, ChemSusChem, 2014, 7, 1372–1385 CrossRef CAS PubMed.
- Y. Chen, C. Xiang, S. Hu and N. S. Lewis, J. Electrochem. Soc., 2014, 161, F1101–F1110 CrossRef CAS PubMed.
- S. Haussener, S. Hu, C. X. Xiang, A. Z. Weber and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3605–3618 CAS.
- S. Haussener, C. X. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 CAS.
- S. Hu, C. X. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 CAS.
- C. Xiang, Y. Chen and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3713–3721 CAS.
- M. R. Singh, J. C. Stevens and A. Z. Weber, J. Electrochem. Soc., 2014, 161, E3283–E3296 CrossRef CAS PubMed.
- S. Srinivasan, Fuel cells: from fundamentals to applications, Springer Science & Business media, 2006 Search PubMed.
- C. C. L. McCrory, S. H. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- S. K. Zecevic, J. S. Wainright, M. H. Litt, S. L. Gojkovic and R. F. Savinell, J. Electrochem. Soc., 1998, 145, 3308–3311 CrossRef PubMed.
- K. Kadakia, M. K. Datta, O. I. Velikokhatnyi, P. H. Jampani and P. N. Kumta, Int. J. Hydrogen Energy, 2014, 39, 664–674 CrossRef CAS PubMed.
- J. R. McKone, N. S. Lewis and H. B. Gray, Chem. Mater., 2014, 26, 407–414 CrossRef CAS.
- M. A. Modestino, K. A. Walczak, A. Berger, C. M. Evans, S. Haussener, C. Koval, J. S. Newman, J. W. Ager and R. A. Segalman, Energy Environ. Sci., 2013, 7, 297–301 Search PubMed.
- J. Jin, K. Walczak, M. R. Singh, C. Karp, N. S. Lewis and C. X. Xiang, Energy Environ. Sci., 2014, 7, 3371–3380 CAS.
- S. M. H. Hashemi, M. A. Modestino and D. Psaltis, Energy Environ. Sci., 2015, 8, 2003–2009 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, Fundamentals and Applications, Wiley, 2000 Search PubMed.
- C. A. Sequeira, D. M. Santos, B. Šljukić and L. Amaral, Braz. J. Phys., 2013, 43, 199–208 CrossRef CAS.
- H. Vogt and R. Balzer, Electrochim. Acta, 2005, 50, 2073–2079 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ee01721a |
| This journal is © The Royal Society of Chemistry 2015 |